Элемент х1 не будет стоять рядом с элементом х6 – Множество, состоящее из шести элементов х1-х6, упорядочили всеми возможными способами. Сколько таких способов? — Вебджем.рф

Содержание

Решение задач Задачи 📝 к экзамену по курсу «Дискретная математика» (для

Задачи к экзамену по курсу «Дискретная математика» (для вечерней и заочной формы обучения).

Решение задач

Дискретная математика

Заказ выполнен

1.Множество состоящее из шести элементов Х1,Х2,Х3,Х4,Х5,Х6 упорядочили всеми возможными способами. • Сколько таких способов? • В скольких случаях элемент Х2 будет стоять перед элементом Х6? • В скольких случаях элемент Х3 не будет ни первым, ни последним? • В скольких случаях элемент Х5 будет первым по порядку? • В скольких случаях элемент Х2 будет первым по порядку, а элемент Х6 будет последним? • В скольких случаях элемент Х2 будет стоять рядом с элементом Х3? • В скольких случаях элемент Х3 не будет стоять рядом с элементом Х4? 2. а) В январе было 10 солнечных дней, а снег шел в течение 25 дней, докажите, что в течение 4 дней было солнце, и шел снег. б) Найти количество натуральных чисел, меньших 100, которые делятся на 3 или 7. в) Найти количество натуральных чисел, не больших 1000, которые делятся или на 10, или на 15 или на 36. г) Найти количество натуральных чисел, меньших 100, которые не делятся на 5 и 11. д) Номерной знак автомобиля состоит из двух пар чисел (например, 42-91, 17-44). Сколько номеров автомобилей, где две одинаковые цифры присутствуют в одной паре (например, 55-12, 43-77, 33-00, 66-66). е) Найти количество натуральных чисел, не больших 1000, которые делятся или на 15, или на 20 или на 24. 3. Доказать равносильность формул логики высказываний (с помощью равносильных преобразований или с помощью таблиц истинности). • • • • • •

Это место для переписки тет-а-тет между заказчиком и исполнителем.
Войдите в личный кабинет (авторизуйтесь на сайте) или зарегистрируйтесь, чтобы
получить доступ ко всем возможностям сайта.

Потапов М. К., Шевкин А. В. Алгебра и начала математического анализа. 10 класс

Глава I

Корни, степени, логарифмы

В этой главе повторяются, расширяются и систематизируются известные учащимся из курса алгебры основной школы сведения о действительных числах, вводятся понятия корня степени

n, степени с рациональным показателем, а затем и с действительным показателем, понятие логарифма числа. Тем самым завершается линия развития понятия числа. Дальнейшее расширение множества чисел — введение комплексных чисел — завершается в учебнике для 11 класса (профильное обучение).
      Функциональная линия в первой главе строится следующим образом. Сначала повторяется классическое определение функции по Лобачевскому — Дирихле, изучается функция у = хⁿ, затем функция y=xn. После введения понятия степени с действительным показателем вводится показательная функция, а после введения логарифмов и логарифмическая функция.
      Линия уравнений и неравенств начинается повторением изученного в девятилетней школе — повторяются способы решения рациональных уравнений и неравенств. Завершается глава решением показательных и логарифмических уравнений и неравенств.
      В профильных классах предусмотрено изучение дополнительных тем, связанных с решением алгебраических уравнений высших степеней.

В результате изучения главы I учащиеся должны знать основные определения и свойства, связанные с понятиями действительного числа, корня степени n, степени с действительным показателем и логарифма, уметь преобразовывать несложные выражения, содержащие корни степени n, степени с дробным показателем и логарифмы, знать свойства и уметь строить графики функций у = хⁿ, y=xn, показательной и логарифмической; уметь решать простейшие показательные, логарифмические, а также сводящиеся к ним уравнения и неравенства.

§ 1. Действительные числа

1.1. Понятие действительного числа

1.2. Множества чисел. Свойства действительных чисел

Материал первых двух пунктов § 1 нацелен на повторение с некоторым обобщением известных учащимся сведений о действительных числах, модуле числа, системе координат на прямой и плоскости. Надо обратить внимание учащихся на то, что множество чисел может быть замкнутым относительно некоторой операции, например множество натуральных чисел замкнуто относительно операций сложения и умножения: сумма и произведение любых двух натуральных чисел являются натуральными числами, а разность и частное не обязательно являются натуральными числами. Стремление «усовершенствовать» множество чисел, сделать выполнимыми в «новом» множестве операции, не всегда выполнимые в «старом», является побудительной причиной для расширения первоначально освоенных множеств чисел. Здесь можно напомнить учащимся некоторые не всегда выполнимые операции, которые стали всегда выполнимыми после расширения множества чисел.

Надо напомнить учащимся, что наряду с бесконечными десятичными периодическими дробями существуют и бесконечные десятичные непериодические дроби, которые называют иррациональными числами. Рациональные и иррациональные числа составляют множество всех действительных чисел.

      Сравнивают действительные числа, записанные в виде бесконечных десятичных дробей, поразрядно, т. е. по тем же правилам, по которым сравнивают конечные десятичные дроби.
      Имеется особый случай — дроби с периодом 9. Такие дроби есть другая форма записи конечных десятичных дробей, которые можно записать еще и как бесконечные десятичные дроби с периодом 0. В учебнике приведен пример записи дроби 2,4 в виде дробей с периодами 0 и 9:
      2,4 = 2,4000… = 2,4(0) и 2,4 = 2,3999… = 2,3(9).
      Дроби с периодом 9 обычно не рассматривают, в частности, чтобы избежать путаницы при сравнении бесконечных десятичных дробей, например, дробь 2,4(0) может оказаться «больше самой себя», но записанной в виде 2,3(9).
      Пункт 1.1 учебника завершается представлением действительных чисел точками координатной прямой, системой координат на плоскости.
      При повторении материала данного пункта надо обратить внимание учащихся на

мнемоническое правило записи бесконечной десятичной периодической дроби в виде обыкновенной дроби:
      для того чтобы записать периодическую десятичную дробь в виде обыкновенной дроби, надо в числителе записать разность числа до второго периода и числа до первого периода, в знаменателе записать столько девяток, сколько цифр в периоде, и приписать к ним столько нулей, сколько цифр между запятой и первым периодом.
      Это правило сформулировано в п. 1 дидактических материалов, там же приведены примеры его применения. Применение этого правила можно заменить рассуждениями, которые продемонстрируем на примере.
      Пример. Запишем бесконечную периодическую десятичную дробь 2,1(45) в виде обыкновенной дроби.
      Обозначим дробь буквой х:

тогда

10x

= 21,454545…,
1000x = 2145,454545…,
1000x − 10x = 2145 − 21,
990x = 2145 − 21,
x=2145−21990,
x=11855,

значит,

2,1(45)=11855.

      Замечание 1. Часто возникает вопрос об обосновании мнемонического правила и рассуждений в приведенном примере. Трудность здесь заключена в том, что неясно, что ученик понимает под бесконечной периодической дробью.
      Под бесконечной периодической дробью можно понимать результат деления уголком числителя на знаменатель несократимой дроби, имеющий простой делитель, отличный от 2 и 5. При таком подходе невозможно получить дробь с периодом 9 и можно убедиться в правильности ответа в приведенном примере, разделив уголком 118 на 55, но трудно обосновать мнемоническое правило в общем виде.
      Замечание 2.

Под бесконечной периодической дробью α₀,α₁α₂α₃…α_k… можно понимать сумму ряда α0+α110+α2102+α3103+…+αk10k+…

17 различий, которые больше не поставят нас в тупик

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Время от времени приходится задумываться, а чем отличаются, например, суши от роллов. Или балкон от лоджии. Или проспект от бульвара. Или маслины от оливок…

AdMe.ru решил разобраться в этой путанице и ответить на все популярные вопросы о «разнице между» в одном месте.

1. Маслины и оливки

Вопреки расхожему мнению, маслины и оливки — это плоды одного дерева. Во всем мире, кроме России и стран СНГ, плоды оливкового дерева называют оливками (зелеными или черными).

В русском языке под маслинами подразумевают черные оливки, достигшие полной зрелости. Именно их используют для производства оливкового масла.

2. Суши и роллы

Суши (суси) — это общее название популярного блюда японской кухни из клейкого риса и морепродуктов. Роллы — один из видов суши.

Классические суши представляют собой комочки риса, накрытые рыбой. А роллы — это рулеты из риса с начинкой, завернутые в лист водорослей нори.

В отличие от суши, в состав роллов могут входить любые начинки, в то время как суши готовят только с морепродуктами.

Суши готовят руками, а роллы — при помощи специального коврика-макису.

3. Фортепиано, пианино и рояль

Фортепиано — это общее название класса инструментов, имеющих клавиши и молоточковую механику.

Пианино, как и рояль, — это разновидности фортепиано.

Между собой пианино и рояль отличаются формой и внутренним устройством. В пианино струны, дека и механическая часть расположены вертикально, а не горизонтально, поэтому пианино меньше, чем рояль.

4. Проспект и бульвар

Проспект является широкой проезжей улицей, предназначенной для движения транспорта. Проспектами, как правило, называют центральные улицы или те, которые соединяют важные части города.

Бульвар представляет собой аллею с обязательной пешеходной зоной и зелеными насаждениями. Бульвары могут находиться в любой части города, часто являясь зеленой «отдушиной» в промзонах или возле загруженных дорог.

5. Балкон и лоджия

Лекция 5. Задача о беспорядках

Пусть имеется конечное упорядоченное множество элементов {1,…, n}. Из этих элементов могут быть образованы перестановки a₁,…, a_n (a_iÎ{1,…,n}). Число всех возможных перестановок – n!. Среди этих n! перестановок есть такие, что ни один элемент не стоит на своём месте (a_i¹i, i= 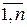). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n-м месте. Такие перестановки называются беспорядками.

Число беспорядков из n элементов обозначается D_n (ясно, что D_n<n!).

Теорема.Число беспорядков из n элементов равно:

# Обозначим через свойство p_i – «i-й элемент стоит на i-м месте». Тогда по формуле решета .

Общее число перестановок n элементов – n! Число перестановок, где i-й элемент стоит на i-м месте, равно (n-1)! (ставим i-й элемент на i-е место, а оставшиеся n-1 элементы переставляем (n-1)! способами). При этом сам i-й элемент можно выбрать способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно .

Число перестановок, где i-й элемент стоит на i-м месте, а j-й на j-м (i¹j), равно (n-2)!, при этом i-й и j-й элементы можно выбрать 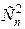способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах – .

Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента – . Число перестановок, где на своих местах стоят хотя бы r элементов – . Число перестановок, где все элементы стоят на своих местах . Подставляем в формулу решета: #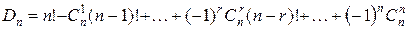

Следствие 1.

Так как ,

то .

Следствие 2.

Так как , то .

Следствие 3.

Рекуррентная формула для числа беспорядков: .

Следствие 4.

# По рекуррентной формуле из следствия 3 получаем или 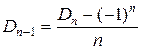. При n=1 получаем . По формуле из следствия 1 получаем . Следовательно, . #

Следствие 5.

Ещё одна рекуррентная формула для числа беспорядков: .

# Рассмотрим n элементов x₁, x₂, … , x_n. Переставим их так, чтобы получить беспорядок. Начнём с x₁: возьмём x₁ и подставим его на место i-го элемента (i¹1). Тогда x_i можно поставить на либо на первое место, либо на какое-то другое, кроме i-го. Если x₁ стоит на i-м месте, а x_i – на 1-ом, то число таких беспорядков – D_n_-2 (т.е. число беспорядков оставшихся n-2 элементов). Если x₁ не стоит на первом месте, то такой беспорядок определяется условием:

x₂ не стоит на 2-м месте,

x₃ не стоит на 3-м месте,

…

x_i_-1 не стоит на (i-1)-м месте,

x_i не стоит на 1-м месте,

x_i+₁ не стоит на (i+1)-м месте,

…

x_n не стоит на n-м месте.

Всего здесь n-1 элемент, то есть число таких беспорядков – D_n_-1.

Итак, если x₁ стоит на i-ом месте, то число таких беспорядков D_n_-1+D_n-2. Но x₁ можно поставить на любое из (n-1) мест (кроме 1-го). Для каждой установки x₁ справедливы приведённые выше рассуждения.

Таким образом, общее число беспорядков – (n-1)(D_n-₁+D_n-2). #

Для проверки полученной формулы вычислим количество беспорядков для некоторых значений n по рекуррентной и прямой формулам. По следствию 4, D₀=1, D₁=0.

Для строгого доказательства правильности рекуррентной формулы, проверим ее в общем виде.

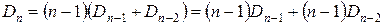Из следствия 3 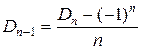, следовательно, . Тогда

. Подставим этот результат в рекуррентную формулу:

. Получили формулу из следствия 3.

Обозначим через D_n,r число перестановок, в которых на своих местах остаются r элементов, а остальные (n-r) образуют беспорядок. Ясно, что D_n,n=1 (все элементы на своих местах), и D_n,0=D_n (ни одного элемента нет на своём месте).

Теорема. .

# r элементов, стоящих на своём месте, можно выбрать из n элементов способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых D_n-r. Следовательно, всего таких перестановок .

С другой стороны, (n-r) элементов, образующих беспорядки, можно выбрать 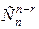способами. Следовательно, . В силу симметричности биномиальных коэффициентов , обе формулы дают один и тот же результат.

Пример.Выстраиваем 5 человек в определённом порядке, после чего 3 из них переставляем так, чтобы они не стояли на своих местах. Сколько таких перестановок?

Ответ: если трое не стоят на своих местах, то оставшиеся двое стоят на своих местах, т.е.

Следствие. .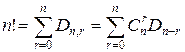

# Из n элементов можно образовать n! перестановок без повторений.

Среди них будет D_n,0 таких, где ни один элемент не стоит на своём месте;

D_n_,1 таких, где по одному элементу стоит на своём месте;

D_n_,2 таких, где по паре элементов стоит на своих местах;

и т.д.;

D_n,n=1 таких, где все элементы стоят на своих местах.

Следовательно, общее число перестановок (n!) равно сумме этих чисел. #

~~Теорема о числе перестановок~~
Функция Эйлера. Доказать, что , где n- натуральное число, p-простые делители числа n. Выразить функцию Эйлера через функцию Мебиуса.

Функция Эйлера

Функция Эйлера φ(n), где n – натуральное число, дает количество натуральных чисел, не превышающих n и взаимно простых с n. Иначе говоря, φ(n)=k, где 0<k£n; (k,n)=1.

Теорема

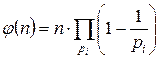, где p_i – все простые делители n. ( — произведение по всем простым делителям числа n).

# В теореме Лежандра заменим a_i на p_i, где p_i – простые делители n.

Тогда 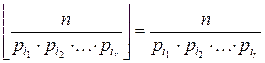(так как p_i делят n нацело).

По теореме Лежандра

. #

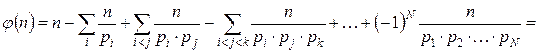
Пример.Определим, сколько чисел, не превышающих 100, взаимно простые с 100. Разложим число 100 на простые сомножители: 100=2·2·5·5=2²5². Таким образом, у числа 100 два простых делителя – 2 и 5. По формуле Эйлера получаем

Таким образом, среди первой сотни есть 40 чисел, взаимно простых с 100.

Функция Мебиуса

Функция Мебиуса m(n), где n – натуральное число, принимает следующие значения:

Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:

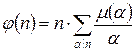Суммирование идет по всем делителям n (а не только по простым делителям).

Пример. Вычислим φ(100), используя функцию Мебиуса.

Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}.

m(1) = 1,

m(2) = (-1)¹= -1 (у двойки один простой делитель – 2)

m(4) = 0 (4 делится на квадрат двойки)

m(5) = (-1)¹= -1 (у 5 один простой делитель – 5)

m(10) = (-1)²= 1 (у 10 два простых делителя – 2 и 5)

m(20) = 0 (20 делится на квадрат двойки)

m(25) = 0 (25 делится на квадрат пятерки)

m(50) = 0 (50 делится и на 2², и на 5⁵)

m(100) = 0 (100 делится и на 2², и на 5⁵)

Таким образом,

Свойство функции Мебиуса: .

Например, n=100, aÎ{1, 2, 4, 5, 10, 20, 25, 50, 100}.

~~Теорема о числе способов выбора~~ ~~k-элементов, среди которых нет двух соседних, из~~ ~~n элементов, расположенных в ряд. Доказать с помощью получения рекуррентной формулы.~~
Теорема о числе сочетаний с повторениями. Доказать с помощью получения рекуррентной формулы.

Шаг 1: Вводим обозначения – обозначим число r-сочетаний с повторениями из n-множества S через f(n,r)

Шаг 2: Начальные условия: f(n,1)=n; f(1,r)=1

Шаг 3: Логические рассуждения

Как правило, из множества S выделяется какой-либо элемент и фиксируется. Чаще всего – первый из ряда.

Тогда относительно нашего случая о любом r-сочетании с повторениями, можно сказать, содержит оно фиксированный элемент или не содержит.

Если содержит, то остальные (r-1) элементов этого r-сочетания (а, значит, r-сочетаний содержащих фиксированный элемент), можно выбрть f(n, r-1) способом.

Если сочетание не содержит, то таких r-сочетаний f(n-1,r).

Т.к. эти случаи взаимно исключают друг друга, то:

f(n,r)= f(n, r-1)+ f(n-1,r)

Шаг 4: Необходимо проверить получившуюся рекуррентную формулу применительно к известному результату.

f(n,0)=1=f(n,1)-f(n-1,1)=n-(n-1)

Шаг 5: Различные построения.

Один из вариантов: последовательно вычислять f(n,2), f(n,3) и т.д. и смотреть есть ли закономерность.

f(n,2)=n(n+1)/2

f(n,3)=n(n+1) (n+2)/6

В общем виде:

f(n,r)=n(n+1)(n+2)….(n+r-1)/r!

Шаг 6: Рекуррентный спуск

Проверка с помощью формулы начальных условий:

f(n,1)=n

f(1,r)=1

S-элементы — Википедия

Материал из Википедии — свободной энциклопедии

Группа →

↓ Период

37	Рубидий

[Kr]5s¹

87	Франций

[Rn]7s¹

s-Элементы в периодической таблице элементов — химические элементы, электронная оболочка которых включает в себя первые два s-электрона. Такие элементы объединяются в группу, называемую s-блок.

К s-элементам относятся:

S-элементы отличаются тем, что в невозбужденном состоянии высокоэнергетичный электрон атомов находится на s-орбитали. Исключая водород и гелий, эти электроны очень легко отщепляются и формируются в положительные ионы при химической реакции. Конфигурация гелия химически стабильна; за счёт этого его относят к инертным газам.

S-элементы (кроме гелия) являются сильными восстановителями и поэтому в свободном виде в природе не встречаются. Элемент в металлическом виде может быть получен только с помощью электролиза расплава соли. Гемфри Дэви, в 1807 и 1808 году, стал первым, кто выделил s-металлы из их солей, за исключением лития, бериллия, рубидия и цезия. Бериллий был впервые выделен из солей независимо двумя учёными: Ф. Вулером и А. А. Бази в 1828 году, в то время как литий был выделен Р. Бунзеном только в 1854 году, который, после изучения рубидия, выделил его спустя 9 лет. Цезий не был выделен в чистом виде вплоть до 1881 года, до того, как Карл Сеттерберг подверг электролизу цианид цезия.

Твёрдость s-элементов в компактном виде (при обычных условиях) может варьироваться от очень малой (все щелочные металлы — их можно разрезать ножом) до довольно высокой (бериллий). Исключая бериллий и магний, металлы очень реакционноспособны и могут быть использованы в сплавах со свинцом в малых количествах (<2 %). Бериллий и магний, ввиду их высокой стоимости, могут быть ценными компонентами для деталей, где требуется твёрдость и лёгкость. Эти металлы являются чрезвычайно важными, поскольку позволяют сэкономить средства при добыче титана, циркония, тория и тантала из их минеральных форм; могут находить своё применение как восстановители в органической химии.

Все элементы, имеющие s-оболочку, являются опасными веществами. Они пожаро-(взрыво-)опасны, требуют особого пожаротушения, исключая бериллий и магний. Храниться должны в инертной атмосфере аргона или углеводородов. Бурно реагируют с водой, продуктом реакции является водород, например:

2Li+2h3O⟶2LiOH+h3↑{\displaystyle {\mathsf {2Li+2H_{2}O\longrightarrow 2LiOH+H_{2}\uparrow }}},

исключая магний, который реагирует медленно, и бериллия, который реагирует только когда его оксидная плёнка снята с помощью ртути. Литий имеет схожие свойства с магнием, так как находится, относительно периодической таблицы, рядом с магнием.

↑ Standard Atomic Weights — 1919.

Дикерсон Р., Грей Г., Хейт Дж. Основные законы химии: В 2-х томах. Пер. с англ. — М.: Мир, 1982. 652 с., ил. — Т. 1. — С. 432—437.

Сочетание — Википедия

Материал из Википедии — свободной энциклопедии

В комбинаторике сочетанием из n{\displaystyle n} по k{\displaystyle k} называется набор k{\displaystyle k} элементов, выбранных из данного множества, содержащего n{\displaystyle n} различных элементов.

Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, k=3{\displaystyle k=3}) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6{\displaystyle n=6}) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать k{\displaystyle k} элементов из множества, содержащего n{\displaystyle n} различных элементов, стоит на пересечении k{\displaystyle k}-й диагонали и n{\displaystyle n}-й строки треугольника Паскаля.^[1]

3х элементные подмножества 5 элементного множества

Число сочетаний из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

(nk)=Cnk=n!k!(n−k)!.{\displaystyle {n \choose k}=C_{n}^{k}={\frac {n!}{k!\left(n-k\right)!}}.}

При фиксированном n{\displaystyle n} производящей функцией последовательности чисел сочетаний (n0){\displaystyle {\tbinom {n}{0}}}, (n1){\displaystyle {\tbinom {n}{1}}}, (n2){\displaystyle {\tbinom {n}{2}}}, … является:

∑k=0n(nk)xk=(1+x)n.{\displaystyle \sum _{k=0}^{n}{\binom {n}{k}}x^{k}=(1+x)^{n}.}

Двумерной производящей функцией чисел сочетаний является

∑n=0∞∑k=0n(nk)xkyn=∑n=0∞(1+x)nyn=11−y−xy.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}{\binom {n}{k}}x^{k}y^{n}=\sum _{n=0}^{\infty }(1+x)^{n}y^{n}={\frac {1}{1-y-xy}}.}

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз. В частности, количество монотонных неубывающих функций из множества {1,2,…,k}{\displaystyle \{1,2,\dots ,k\}} в множество {1,2,…,n}{\displaystyle \{1,2,\dots ,n\}} равно числу сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k}.

Число сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

C(n)k=((nk))=(n+k−1n−1)=(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!⋅(n−1)!.{\displaystyle C_{(n)}^{k}=\left(\!\!{\binom {n}{k}}\!\!\right)={\binom {n+k-1}{n-1}}={\binom {n+k-1}{k}}=(-1)^{k}{\binom {-n}{k}}={\frac {(n+k-1)!}{k!\cdot (n-1)!}}.}

Доказательство

Пусть имеется n{\displaystyle n} типов объектов, причём объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше k{\displaystyle k}) количество объектов каждого типа. Из этого ассортимента выберем k{\displaystyle k} объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через xj{\displaystyle x_{j}} количество выбранных объектов j{\displaystyle j}-го типа, xj≥0{\displaystyle x_{j}\geq 0}, j=1,2,…,n{\displaystyle j=1,2,\dots ,n}. Тогда x1+x2+⋯+xn=k{\displaystyle x_{1}+x_{2}+\dots +x_{n}=k}. Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд k{\displaystyle k} шаров и n−1{\displaystyle n-1} перегородок так, чтобы между (j−1){\displaystyle (j-1)}-й и j{\displaystyle j}-й перегородками находилось ровно xj{\displaystyle x_{j}} шаров. Но таких расстановок в точности (n+k−1k){\displaystyle {\tbinom {n+k-1}{k}}}, что и требовалось доказать.■

При фиксированном n{\displaystyle n} производящей функцией чисел сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} является:

∑k=0∞(−1)k(−nk)xk=(1−x)−n.{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}=(1-x)^{-n}.}

Двумерной производящей функцией чисел сочетаний с повторениями является:

∑n=0∞∑k=0∞(−1)k(−nk)xkyn=∑n=0∞(1−x)−nyn=1−x1−x−y.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}y^{n}=\sum _{n=0}^{\infty }(1-x)^{-n}y^{n}={\frac {1-x}{1-x-y}}.}

Р. Стенли. Перечислительная комбинаторика. — М.: Мир, 1990.

Порядок элемента — Википедия

Порядок элемента в теории групп — наименьшее положительное целое m{\displaystyle m}, такое что m{\displaystyle m}-кратное групповое умножение данного элемента g∈G{\displaystyle g\in G} на себя даёт нейтральный элемент:

gg…g⏟m=gm=e{\displaystyle \underbrace {gg\dots g} _{m}=g^{m}=e}.

Иными словами, m{\displaystyle m} — количество различных элементов циклической подгруппы, порождённой данным элементом. Если такого m{\displaystyle m} не существует (или, эквивалентно, число элементов циклической подгруппы бесконечно), то говорят, что g{\displaystyle g} имеет бесконечный порядок. Обозначается как ord(g){\displaystyle \mathrm {ord} (g)} или |g|{\displaystyle |g|}.

Изучение порядков элементов группы может дать сведения о её структуре. Несколько глубоких вопросов о связи порядка элементов и порядка группы содержатся в различных проблемах Бёрнсайда, некоторые из них остаются открытыми.

Порядок элемента равен единице тогда и только тогда, когда элемент является нейтральным.

Если всякий не нейтральный элемент в G{\displaystyle G} совпадает со своим обратным (то есть g2=e{\displaystyle g^{2}=e}), то ord(a)=2{\displaystyle \mathrm {ord} (a)=2} и G{\displaystyle G} является абелевой, поскольку ab=(ab)−1=b−1a−1=ba{\displaystyle ab=(ab)^{-1}=b^{-1}a^{-1}=ba}. Обратное утверждение в общем случае неверно: например, (аддитивная) циклическая группа Z6{\displaystyle \mathbb {Z} _{6}} целых чисел по модулю 6 — абелева, но число 2 имеет порядок 3:

2+2+2=6≡0(mod6){\displaystyle 2+2+2=6\equiv 0{\pmod {6}}}.

Для любого целого k{\displaystyle k} тождество gk=e{\displaystyle g^{k}=e} выполнено тогда и только тогда, когда ord(g){\displaystyle \mathrm {ord} (g)} делит k{\displaystyle k}.

Все степени элемента бесконечного порядка имеют также бесконечный порядок. Если g{\displaystyle g} имеет конечный порядок, то порядок gk{\displaystyle g^{k}} равен порядку g{\displaystyle g}, делённому на наибольший общий делитель чисел ord(g){\displaystyle \mathrm {ord} (g)} и k{\displaystyle k}. Порядок обратного элемента совпадает с порядком самого элемента (ord(g)=ord(g−1){\displaystyle \mathrm {ord} (g)=\mathrm {ord} (g^{-1})}).

Порядок любого элемента группы делит порядок группы. Например, в симметрической группе S3{\displaystyle S_{3}}, состоящей из шести элементов, нейтральный элемент e{\displaystyle e} имеет (по определению) порядок 1, три элемента, являющихся корнями из e{\displaystyle e} — порядок 2, а порядок 3 имеют два оставшихся элемента, являющихся корнями элементов порядка 2: то есть, все порядки элементов являются делителями порядка группы.

Частично обратное утверждение верно для конечных групп (теоретико-групповая теорема Коши): если простое число p{\displaystyle p} делит порядок группы G{\displaystyle G}, то существует элемент g∈G{\displaystyle g\in G}, для которого ord(g)=p{\displaystyle \mathrm {ord} (g)=p}. Утверждение не выполняется для составных порядков, так, четверная группа Клейна не содержит элемента порядка четыре.

В любой группе ord(ab)=ord(ba){\displaystyle \mathrm {ord} (ab)=\mathrm {ord} (ba)}.

Не существует общей формулы, связывающей порядок произведения ab{\displaystyle ab} с порядками сомножителей a{\displaystyle a} и b{\displaystyle b}. Возможен случай, когда и a{\displaystyle a}, и b{\displaystyle b} имеют конечные порядки, в то время как порядок произведения ab{\displaystyle ab} бесконечен, также возможно, что и a{\displaystyle a}, и b{\displaystyle b} имеют бесконечный порядок, в то время как ord(ab){\displaystyle \mathrm {ord} (ab)} конечен. Пример первого случая — в симметрической группе над целыми числами перестановки, задаваемые формулами a(x)=2−x,b(x)=1−x{\displaystyle a(x)=2-x,b(x)=1-x}, тогда ab(x)=x−1{\displaystyle ab(x)=x-1}. Пример второго случая — перестановки в той же группе a(x)=x+1,b(x)=x−1{\displaystyle a(x)=x+1,b(x)=x-1}, произведение которых является нейтральным элементом (перестановка ab(x)=id{\displaystyle ab(x)=\mathrm {id} }, оставляющая элементы на своих местах). Если ab=ba{\displaystyle ab=ba} то можно утверждать, что ord(ab){\displaystyle \mathrm {ord} (ab)} делит наименьшее общее кратное чисел ord(a){\displaystyle \mathrm {ord} (a)} и ord(b){\displaystyle \mathrm {ord} (b)}. Следствием этого факта является, что в конечной абелевой группе порядок любого элемента делит максимальный порядок элементов группы.

Для данной конечной группы G{\displaystyle G} порядка n{\displaystyle n}, число элементов с порядком d{\displaystyle d} (d{\displaystyle d} — делитель n{\displaystyle n}) кратно φ(d){\displaystyle \varphi (d)}, где φ{\displaystyle \varphi } — функция Эйлера, дающая число положительных чисел, не превосходящих d{\displaystyle d} и взаимно простых с ним. Например, в случае S3{\displaystyle S_{3}} φ(3)=2{\displaystyle \varphi (3)=2}, и имеется в точности два элемента порядка 3; при этом данное утверждение не даёт никакой полезной информации относительно элементов порядка 2, поскольку φ(2)=1{\displaystyle \varphi (2)=1}, и очень ограниченную информацию о составных числах, таких как d=6{\displaystyle d=6}, поскольку φ(6)=2{\displaystyle \varphi (6)=2}, и в группе S3{\displaystyle S_{3}} имеется нуль элементов порядка 6.

Гомоморфизмы групп имеют свойство понижать порядок элементов. Если f:G→H{\displaystyle f:G\to H} является гомоморфизмом, и g∈G{\displaystyle g\in G} — элемент конечного порядка, то ord(f(g)){\displaystyle \mathrm {ord} (f(g))} делит ord(g){\displaystyle \mathrm {ord} (g)}. Если f{\displaystyle f} инъективно, то ord(f(g))=ord(g){\displaystyle \mathrm {ord} (f(g))=\mathrm {ord} (g)}. Этот факт может быть использован для доказательства отсутствия (инъективного) гомоморфизма между двумя какими-либо заданными группами. (Например, не существует нетривиального гомоморфизма h:S3→Z5{\displaystyle h:S_{3}\to \mathbb {Z} _{5}}, поскольку любое число, за исключением нуля, в Z5{\displaystyle \mathbb {Z} _{5}} имеет порядок 5, а 5 не делит ни один из порядков 1, 2 и 3 элементов S3{\displaystyle S_{3}}.) Другим следствием является утверждение, что сопряжённые элементы имеют одинаковый порядок.

Курош А.Г. Теория групп. — Москва: Наука, 1967. — ISBN 5-8114-0616-9.
Мельников О. В., Ремесленников В. Н., Романьков В. А. . Глава II. Группы // Общая алгебра / Под общ. ред. Л. А. Скорнякова. — М.: Наука, 1990. — Т. 1. — С. 66—290. — 592 с. — (Справочная математическая библиотека). — 30 000 экз. — ISBN 5-02-014426-6.

Элемент х1 не будет стоять рядом с элементом х6 – Множество, состоящее из шести элементов х1-х6, упорядочили всеми возможными способами. Сколько таких способов?