II Градиент
Определение
2.Вектор, проекциями которого служат
частные производные функции
,
называется градиентом функции
.
Для
функции трёх переменных 
:
.
Связь градиента с производной по направлению даётся следующей теоремой.
Теорема 2.Производная функции по направлению есть проекция её градиента на это направление:
Доказательство.Проекция вектора на ось – это проекция вектора на орт оси. Проекцию же вектора на вектор можно найти, используя скалярное произведение:
.
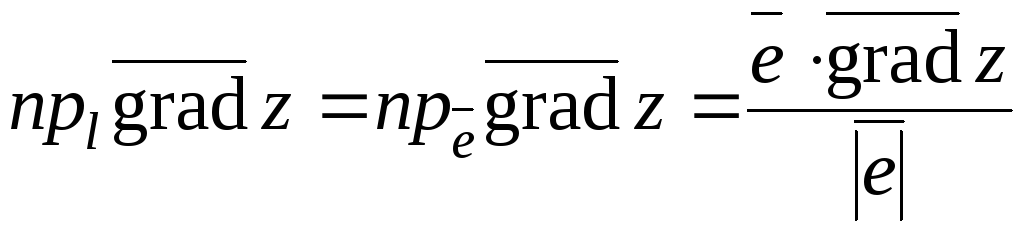Учитывая, что 
и
,
причём
,
получим:
.
Правая часть этого равенства в силу Теоремы 1 есть производная по направле-нию. Теорема доказана.
Следствие 1.Производная функции
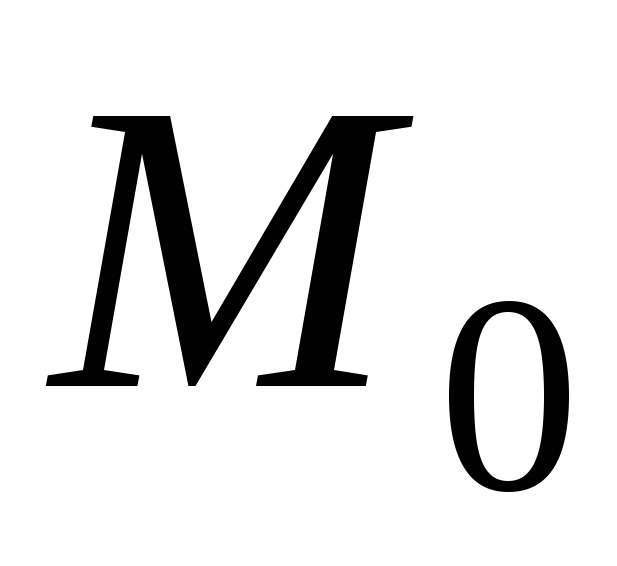по направлению оси
достигает максимума, когда это направление
совпадает с градиентом функции, причём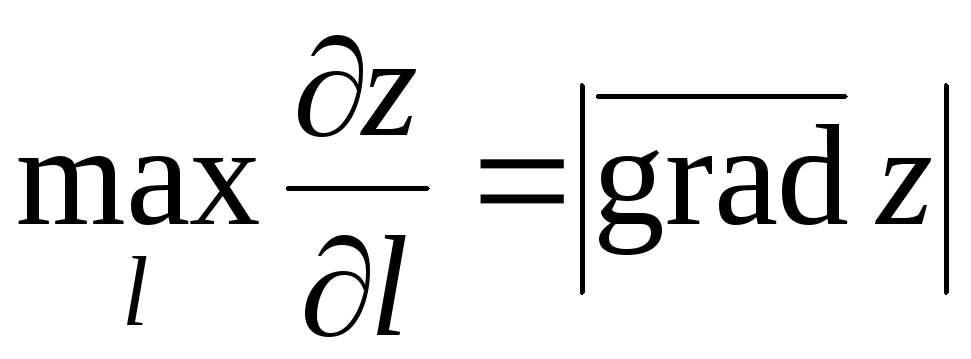 
.
Таким образом, градиент функции в данной точке характеризует направление и величину максимальной скорости возрастания функции в данной точке.
Следствие 2.Производная функции по направлению, перпендикулярному её градиенту, равна нулю.
III Линии и поверхности уровня
Очень часто, чтобы
яснее представить себе график функции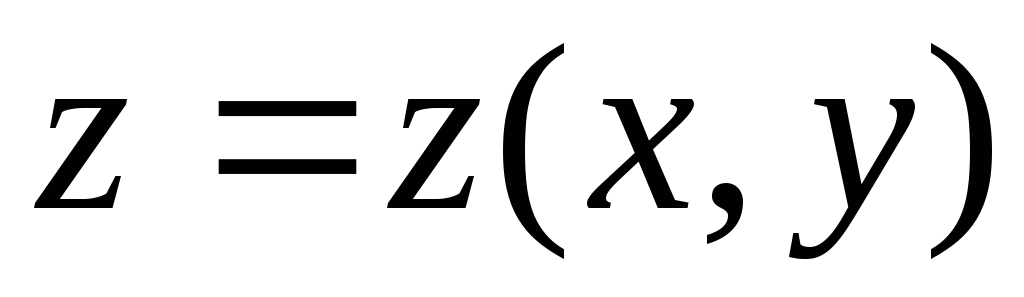 
(т.е. некоторую поверхность) используют
т.н. линии уровня.
Определение
2.Линией уровня функции
называют линию (в области определения
),
вдоль которой функция принимает
постоянное значение, т.е. линию, уравнение
которой имеет вид
,
где
– константа.
Например, для
функции 
,
линии уровня – это два семейства (
и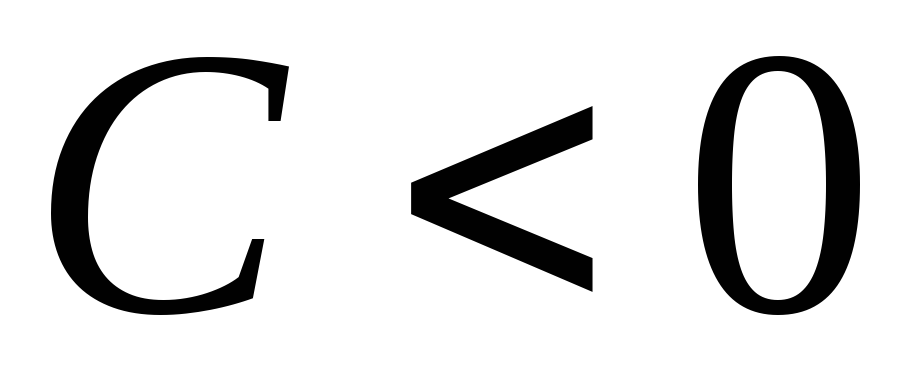
)
сопряжённых гипербол, а так же биссектрисы
координатных углов (
Для функции трёх
переменных 
аналогично вводится понятие поверхности
уровня, т.е. поверхности, определяемой
уравнением
.
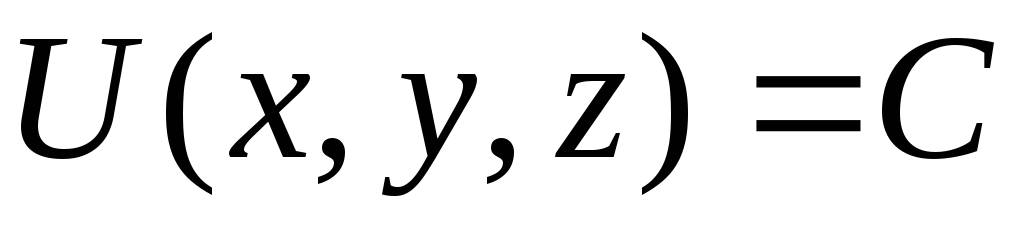Следствие 3.Градиент функции в заданной точке перпендикулярен линии (поверхности) уровня функции, проходящей через эту точку, т.е. направлен по нормали к линии (поверхности) уровня.
Доказательство.(Для функции двух переменных). Рассмотрим
уравнение линии уровня функции
:
Это уравнение
определяет неявную функцию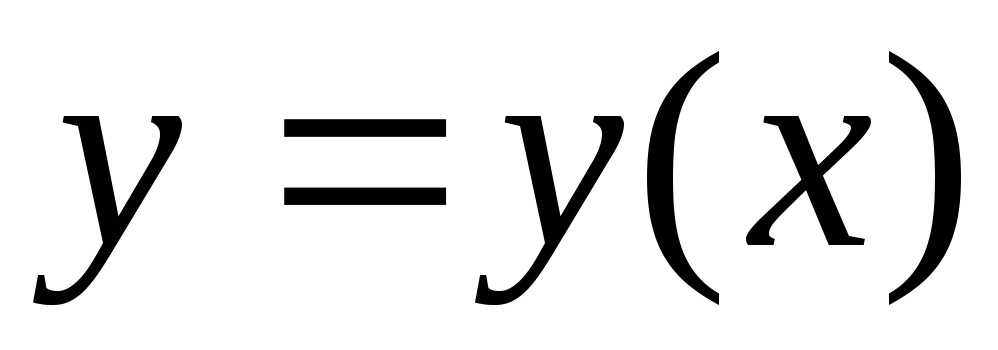 
и её производная имеет вид:
.
Уравнение нормали к графику
в точке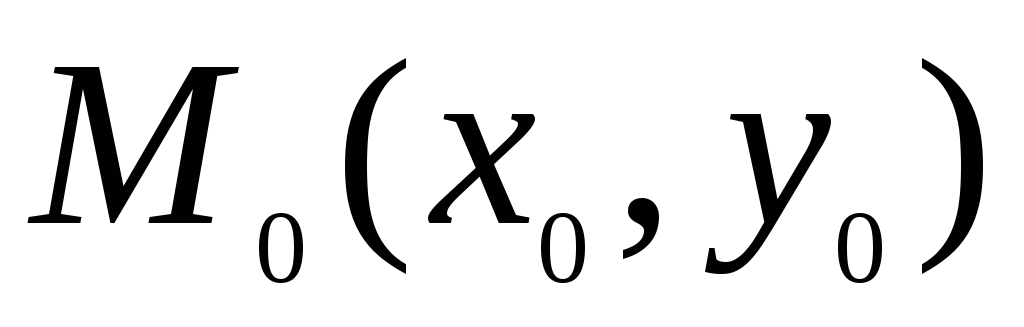
:
.
В нашем случае: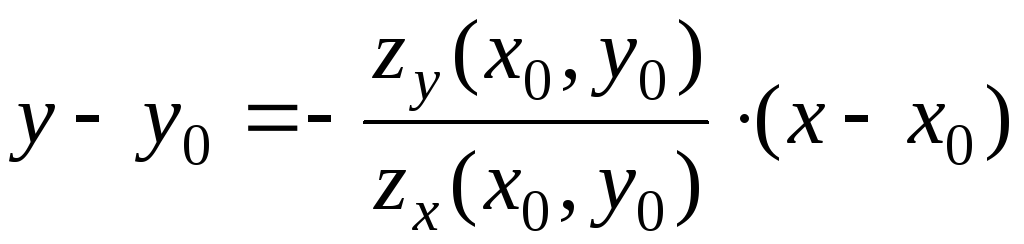 
.
Это уравнение легко переписать в
канонической форме:
.
Из которой следует, что направляющий вектор нормали . Это и означает, что градиент функции направлен по нормали к линии уровня этой функции.
Пример.Для функции
линии уровня :
– это семейство эллипсов
.
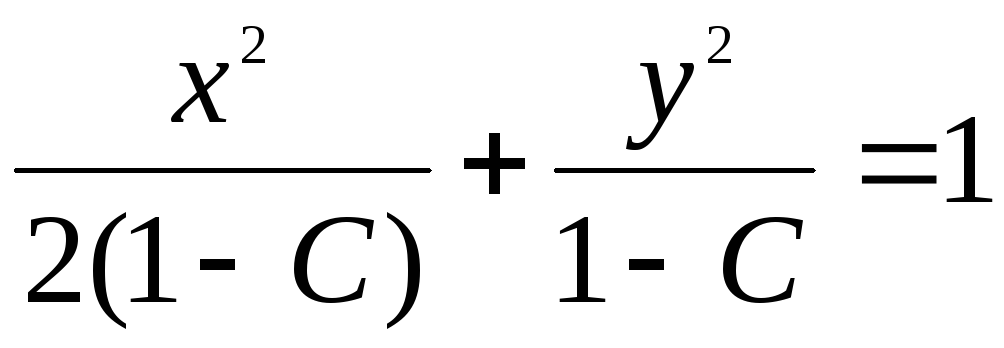Проверим, что
семейство парабол 
пересекает все эти эллипсы под прямым
углом. Дифференцируем уравнение эллипсов
по
:
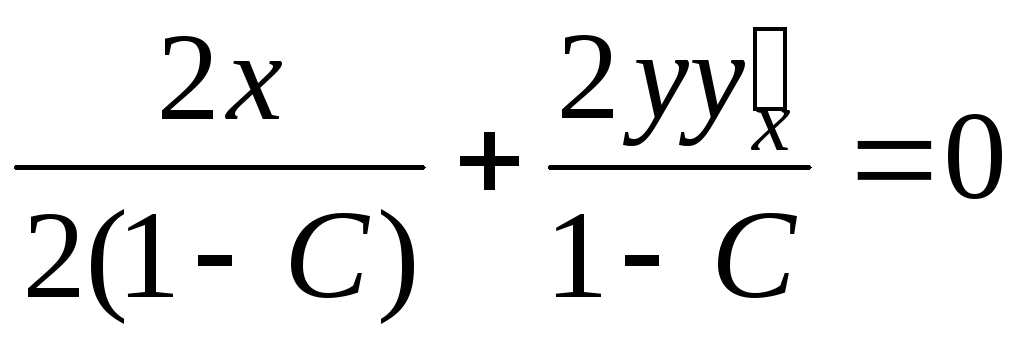
Отсюда угловой коэффициент касательной к эллипсу (в произвольной точке):
.Для параболы тот же коэффициент имеет вид:
.
Пусть 
– точка пересечения какого-либо эллипса
с некоторой параболой. Тогда
и произведение угловых коэффициентов
касательных в этой точке:
.
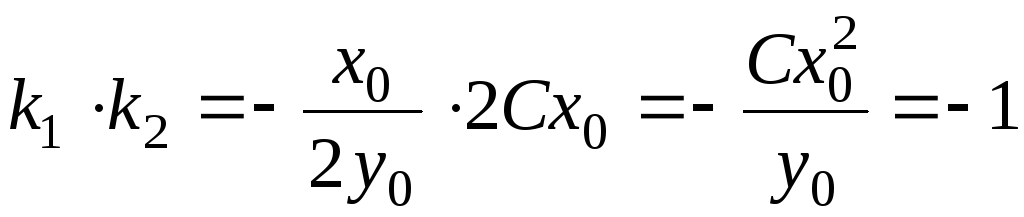Отсюда следует,
что касательные перпендикулярны, т.е.
рассмотренные семейства
взаимно-перпендикулярны. Градиент
функции 
в точке
,
которая проходит через
,
причём в сторону вершины параболы, ибо
начало координат – это абсолютный
максимум данной функции. Одна интерпретация
полученного результата. Поверхность,
определяемая рассмотренной функции, –
это эллиптический параболоид с вершиной
в точке 
,
расположенный ниже плоскости
.
Потоки воды с такой поверхности стекают
по траекториям, проекциями которых
служат параболы семейства
.
Градиент функции нескольких переменных | matematicus.ru
Градиентом функции называется вектор вида
для функции двух переменных формула градиента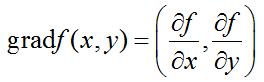
для функции трех переменных формула градиента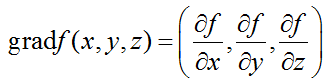
Величина градиента функции, в которой производная имеет наибольшее значение определяется по формуле:
для двух переменных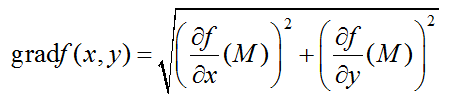
для трех переменных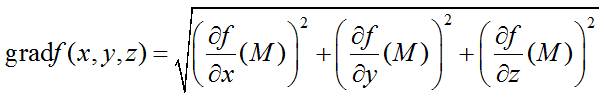
Градиент часто обозначается символом «перевернутого треугольника» — оператор Набла: ∇
Градиент дифференцируемого скалярного поля: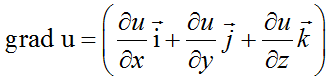
Градиент характеризует скорость изменения функции.
Пример
Найдите градиент функции двух переменных и величину градиента функции
f(x,y)=2y3+4x2
в точке M(2;1).
Решение
Найдем частные производные функции первого порядка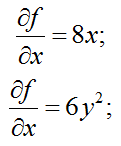
Найдем значение функции в точке M(2;1)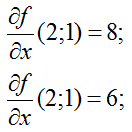
Найдем величину градиента функции в этой точке
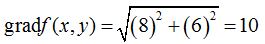
Градиент
Градиент
Производная по направлению. Градиент
Пусть в некоторой области задана функция и точка . Проведем из точки вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку , т.е. .
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется производной от функции
в точке по
направлению вектора и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: ,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции и обозначается
или
(читается «набла у»): .
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
.
Свойства градиента
1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно .
2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.
Примеры решения задач
Пример 1. Найти производную от функции в точке по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
.
Следовательно, для направляющих косинусов вектора получим следующие значения:
.
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна .
Пример 2. Найти градиент функции в точке .
Решение.
Поскольку градиентом функции называется вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, то для решения задачи сначала найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке :
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен .
Пример 3. Найти производную функции в точке по направлению градиента функции в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
В данном случае вектор совпадает
с градиентом функции
в точке :
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: .
Найдем направляющие косинусы вектор по формулам:
.
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке по
направлению градиента функции
в той же точке равна 1.
Задания для самостоятельной работы
1. Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке .
Ответ: .
5. Найти градиент функции
в точке .
Ответ: .
6. Найти градиент функции
в точке .
Ответ: .
Градиент — это… Что такое Градиент?
Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.
Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве.
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным.
Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Стандартные обозначения:
или, с использованием оператора набла,
— вместо может быть любое скалярное поле, обозначенное любой буквой, например — обозначения градиента поля V.
Определение
Для случая трёхмерного пространства градиентом скалярной функции координат , , называется векторная функция с компонентами
- , , .
Или, использовав для единичных векторов по осям прямоугольных декартовых координат :
Если — функция переменных , то её градиентом называется -мерный вектор
компоненты которого равны частным производным по всем её аргументам.
- Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.
- Оператором градиента (обозначаемым обычно, как говорилось выше, или ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто «градиентом».
Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена , то есть линейную (в случае общего положения она же главная) часть изменения при смещении на . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:
или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Пример
Например, градиент функции будет представлять собой:
В физике
В различных отраслях физики используется понятие градиента различных физических полей.
Например, напряженность электростатического поля есть минус градиент электрического потенциала, напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Сила в классической механике есть минус градиент потенциальной энергии.
В естественных науках
Понятие градиента находит применение не только в физике, но и в смежных и даже сравнительно далеких от физики науках (иногда это применение носит количественный, а иногда и просто качественный характер).
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по какому-то направлению температуры среды и т. д.
Градиент таких величин может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз.
Геометрический смысл
Рассмотрим семейство линий уровня функции :
Нетрудно показать, что градиент функции в точке перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности , то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъема в данной точке.
Связь с производной по направлению
Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции по направлению равняется скалярному произведению градиента на единичный вектор :
Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.
Градиент в ортогональных криволинейных координатах
где — коэффициенты Ламе.
Полярные координаты (на плоскости)
Коэффициенты Ламе:
Отсюда:
Цилиндрические координаты
Коэффициенты Ламе:
Отсюда:
Сферические координаты
Коэффициенты Ламе:
- .
Отсюда:
См. также
Литература
1. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Учебное пособие для физико-математических специальностей университетов, 1986. стр.30