градиент калькулятор онлайн
Вы искали градиент калькулятор онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и градиент найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «градиент калькулятор онлайн».
.jpg)
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как градиент калькулятор онлайн,градиент найти,градиент онлайн калькулятор,градиент функции в точке онлайн калькулятор,градиент функции онлайн,калькулятор онлайн градиент,найти градиент,найти градиент функции в точке онлайн,найти градиент функции в точке онлайн калькулятор,онлайн калькулятор градиент. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и градиент калькулятор онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, градиент онлайн калькулятор).
Где можно решить любую задачу по математике, а так же градиент калькулятор онлайн Онлайн?
Решить задачу градиент калькулятор онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| Основные функции
модуль x: abs(x)
| 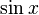 : sin[x] или Sin[x] : sin[x] или Sin[x]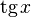 : tan[x] или Tan[x] : tan[x] или Tan[x] : cot[x] или Cot[x] : cot[x] или Cot[x]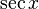 : sec[x] или Sec[x] : sec[x] или Sec[x]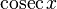 : csc[x] или Csc[x] : csc[x] или Csc[x]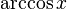 : ArcCos[x] : ArcCos[x]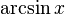 : ArcSin[x] : ArcSin[x]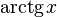 : ArcTan[x] : ArcTan[x]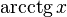 : ArcCot[x] : ArcCot[x]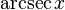 : ArcSec[x] : ArcSec[x]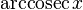 : ArcCsc[x] : ArcCsc[x]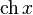 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 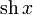 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]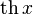 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]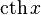 : coth[x] или Coth[x] : coth[x] или Coth[x] : sech[x] или Sech[x] : sech[x] или Sech[x]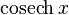 : csch[x] или Csch[е] : csch[x] или Csch[е]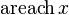 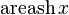 : ArcSinh[x] : ArcSinh[x]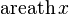 : ArcTanh[x] : ArcTanh[x]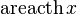 : ArcCoth[x] : ArcCoth[x] : ArcSech[x] : ArcSech[x]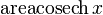 : ArcCsch[x] : ArcCsch[x] |
Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
4. Тригонометрический калькулятор онлайн — примеры
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце — знак равенства.

- [Inv] – обратная функция для sin, cos, tan, переключает интерфейс на другие функции
- [Ln] – натуральный логарифм по основанию «e»
- [ ( ] и [ ) ] — вводит скобки
- [Int] – отображает целую часть десятичного числа
- [Sinh] — гиперболический синус
- [Sin] – синус заданного угла
- [X2] – возведение в квадрат (формула x^2)
- [n!] — вычисляет факториал введенного значения — произведение n последовательных чисел, начиная с единицы до самого введенного числа, например 4!=1*2*3*4, то есть 24
- [Dms] – переводит из десятичного вида в формат в градусы, минуты, секунды.
- [Cosh] — гиперболический косинус
- [Cos] – косинус угла
- [xy] – возведение икса в степ. игрик (формула x^y)
- [y√x] – извлечение корня в степени y из икс
- [Pi] – число Пи, выдает значение Pi для расчетов
- [tanh] — гиперболический тангенс
- [tan] – тангенс угла онлайн, tg
- [X3] — помогает возвести в степень 3, в куб (формула x^3)
- [3√x] — извлечь корень кубический
- [F – E] — переключает ввод чисел в экспоненциальном представлении и обратно
- [Exp] — позволяет вводить данные в экспоненциальном представлении.
- [Mod] — позволяет нам вычислить остаток от деления одного числа на другое
- [Log] – рассчитывает десятичный логарифм
- [10^x] – возведение десяти в произвольную степень
- [1/X] — подсчитывает обратную величину
- [e^x] – Возведение числа Эйлера в степень
- [Frac] – отсекает целую часть, оставляет дробную
- [sinh-1] – обратный гиперболический синус
- [sin-1] – арксинус или обратный синус, arcsin или 1/sin
- [deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее
- [cosh-1] — обратный гиперболический косинус
- [cos-1] – аркосинус или обрат. косинус arccos или 1/cos
- [2*Pi] – рассчитывает число Пи, помноженное на два
- [tanh-1] – обрат. гиперболический тангенс
- [tan-1] – арктангенс или обратный тангенс, arctg
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерах
Как возвести в степень
Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[xy] «икс в степени игрик», [X2] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Найти градиент, дивергенцию, ротор | UpByte.Net
В области \(V\) задано скалярное поле, если каждой точке \(M\) из \(V\) поставлено в соответствие число \(u\left(M \right)\). Скалярное поле \(u\left(M \right)\) называется дифференцируемым в точке \(M_{0}\) из области \(V\), если приращение поля \(\Delta u\) в этой точке можно представить в виде: \(\Delta u=g\cdot \Delta r+o\left(\rho \right)\), где \(\rho =\rho \left(M_{0},M \right)\) — расстояние между точками \(M_{0}\) и \(M\), \(\Delta u=u\left(M \right)-u\left(M_{0} \right)\). Вектор \(g\left(M_{0} \right)\) называется градиентом дифференцируемого в точке \(M_{0}\) скалярного поля. В декартовой системе координат \[grad u=\frac{\partial u}{\partial x}i+\frac{\partial u}{\partial y}j+\frac{\partial u}{\partial z}k\] Если каждой точке \(M\) из области \(V\) поставлен в соответствие некоторый вектор \(F\left(M \right)\), то говорят, что в \(V\) задано векторное поле. Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля. Оператор дивергенции, примененный к полю \(F\), обозначается \(divF\) или \(\bigtriangledown \cdot F\). \[div F=\lim_{V\rightarrow 0}\frac{P_{F}}{V}\] где \(P_{F}\)-поток векторного поля \(F\) через сферическую поверхность площадью \(S\), ограничивающую объем \(V\). Ротор — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Обозначается \(rot\) или \(curl\), вычисляется по формуле \(rot F = \bigtriangledown \times F\).С помощью нашего решебника вы можете вычислить градиент, дивергенцию, ротор векторного поля, выполнить другие операции векторного анализа. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку «Решить».
Вычислить градиент функции
grad sin(x^2 y)
del z e^(x^2+y^2)
grad of a scalar fieldВычислить градиент функции в полярных координатах
grad sqrt(r) cos(theta)Вычислить дивергенцию векторного поля
div (x^2-y^2, 2xy)
div [x^2 sin y, y^2 sin xz, xy sin (cos z)]
divergence calculatorВычислить ротор векторного поля
curl [-y/(x^2+y^2), -x/(x^2+y^2), z]
rotor operatorВычислить Лапласиан функции
Laplace e^x sin y
Laplace x^2+y^2+z^2
laplacian calculatorВычислить выражения
div (grad f)
curl (curl F)
grad (F . G)
Инженерный калькулятор онлайн
Современный уклад жизни требует постоянной динамики. Производя расчеты на калькуляторе, мы заметно экономим свое время, не рискуем в чем-то ошибиться и получаем точный результат. Благодаря изобретению данного устройства, многие люди забыли что такое недостачи и погрешности в расчетах. Однако калькулятор калькулятору рознь, и если примитивные вычислительные функции можно сделать на математической модели, то сложнейшие расчеты возможно совершить только при помощи инженерной. Отныне приобретать данное чудо современной техники не нужно – достаточно обратиться за помощью к нашему инженерному калькулятору онлайн! Программа работает без дополнительной установки – достаточно зайти на электронную страницу и начать действовать.
Функции инженерного калькулятора онлайн
Калькулятор математического типа поможет вам совершить только примитивные расчеты. С его помощью можно сделать то, чему нас учили в начальных классах средней школы:
- сложение;
- вычитание;
- деление;
- умножение;
- вычитание процентов;
- возведение числа в степень;
- нахождение корня квадратного.
Инженерный калькулятор онлайн включает в себя все эти и дополнительные функции, которые необходимы для проведения сложных расчетов. Теперь вам не придется тратить дополнительные деньги на покупку этого устройства, ведь сделать вычисления можно на нашем сайте.
Помимо вышеперечисленных, наш универсальный калькулятор поможет вам выполнить такие расчеты:
Нахождение:
- синуса угла;
- тангенса;
- косинуса;
- котангенса;
- арксинуса;
- арктангенса;
- арккосинуса;
- арккотангенса.
Интерфейс инженерного калькулятора онлайн
Выполнить все вышеперечисленные расчеты достаточно просто. Наш инженерный калькулятор онлайн обладает понятным интерфейсом, а потому работать с ним весьма удобно. По своему виду он полностью имитирует настоящий калькулятор, поэтому долгого изучения функций вам не потребуется. Несмотря на это мы прилагаем подробную инструкцию и описание каждой клавиши.
Пользоваться нашей программой выгодно еще и потому, что расчеты производятся моментально – вам не нужно обновлять страницу сайта, ведь калькулятор работает во флеш-режиме. Ежедневно нашей программой пользуется огромное количество людей. Среди них ученики высших заведений, преподаватели, архитекторы-проектировщики, ученые и другие люди, заинтересованные в точности расчетов. Инженерный калькулятор онлайн не требует скачивания и установки дополнительных плагинов, а потому вы можете начать пользоваться им прямо сейчас!
Градиент и производная по направлению. Контрольные онлайн
Градиент и производная по направлению
Даны скалярное поле точки , .
Найти:
а) градиент поля в точке ;
б) производную функции в точке по направлению от точки к точке . Решение а) Градиент поля в точке вычисляется по формуле .
Найдем частные производные данной функции и их значения в точке :
,
,
.
Следовательно, .
б) Производная скалярного поля по направлению вектора в точке вычисляется по формуле , где , , .
Для решаемой задачи , , ,
, , , . Следовательно, .


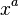 : x^a
: x^a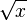 : Sqrt[x]
: Sqrt[x]![\sqrt[n]{x}](/800/600/https/upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n)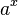 : a^x
: a^x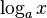 : Log[a, x]
: Log[a, x]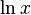 : Log[x]
: Log[x]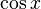 : cos[x] или Cos[x]
: cos[x] или Cos[x]