Градиент — 15 Сентября 2015 — Примеры решений задач
Определение. Вектор с координатами называется градиентом функции u=f(x,y,z) и обозначается
С помощью оператора Гамильтона ( или набла-оператора)
можно кратко записать градиент функции:
Градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.
Модуль градиента определяет крутизну наибольшего ската или подъема поверхности u=f(x,y,z).
Пример 1. Найти градиент grad z, модуль градиента |grad z| для функции z=7-5x2-10y2 в точке M(-5;7)
Решение. Для функции двух переменных градиент находим по формуле
1) Находим частные производные (см. калькулятор частных производных)
2) Подставляем в формулу, получаем градиент функции в произвольной точке
Найти градиент функции можно также с помощью калькулятора
3) Подставляем координаты точки M(-5;7), получаем
4) Находим модуль градиента в точке M(-5;7) по формуле:
Вывод: Если движение происходит в направлении градиента функции (50;-140), то получаем скорость максимального изменения функции 148,66 в точке M(-5;7).
Если движение будет происходить в других направлениях, то скорость будет меньше. Покажем это на примере.
Пример 2. Найти скорость изменения функции z=7-5x2-10y2 в точке M(-5;7) по направлению вектора l(2;-3).
Решение. Пункты 1),2) и 3) совпадают с решением примера 1.
4) Скорость изменения функции z=7-5x2-10y2 в точке M(-5;7) по направлению вектора l(2;-3) находим по формуле производной по направлению:
Lection15
Лекция 15. «Дифференцирование функции нескольких переменных»Градиент функции двух переменных и производная по направлению.
Определение. Градиентом функции

называется вектор
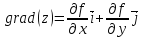 .
.
Иначе, этот вектор может быть записан следующим образом:
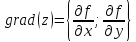
или

или

Как видно из определения градиента функции, компонентами вектора градиента являются частные производные функции.
Пример. Вычислить градиент функции

в точке A(2,3).
Решение. Вычислим частные производные функции.


В общем виде градиент функции имеет вид:
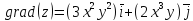 =
= 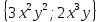
Подставим координаты точки A(2,3) в выражения частных производных


В градиент функции в точке A(2,3) имеет вид:
 =
= 
Аналогично можно определить понятие градиента функции трех переменных:
Определение. Градиентом функции от трех переменных

называется вектор
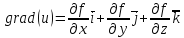
Иначе, этот вектор может быть записан следующим образом:

Определение производной по направлению.
Пусть задана функция двух переменных

и произвольный вектор

Рассмотрим приращение этой функции, взятое вдоль данного вектора

Т.е.
вектор 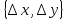 коллинеарный по отношению к вектору
коллинеарный по отношению к вектору  .
Длина приращения аргумента
.
Длина приращения аргумента
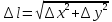
Производной по некоторому направлению называется предел отношения приращения функции вдоль данного направления на длину приращения аргумента, когда длина приращения аргумента стремиться к 0.

Формула для вычисления производной по направлению.
Исходя из определения градиента, производную функции по направлению, можно посчитать следующим образом.
Пусть

некоторый вектор. Вектор с тем же направлением, но единичной длины назовем

Координаты этого вектора вычисляются следующим образом:

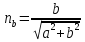
Из
определения производной по направлению  ,
производная по направлению
,
производная по направлению 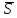

Правая часть этой формулы представляет собой скалярное произведение двух векторов

И

Поэтому, производную по направлению можно представить в виде следующей формулы:

Из этой формулы следует несколько важных свойств вектора градиента.
Производная в данной точке по направлению вектора S имеет наибольшее значение, если направление вектора S совпадает с направлением градиента; это наибольшее значение производной равно |
|.
Производная по направлению вектора, перпендикулярного к вектору
 равна нулю.
равна нулю.
Первое свойство градиента следует из того очевидного факта, что скалярное произведение двух векторов принимает наибольшее значение, когда вектора совпадают по направлению. Второе свойство следует из того, что скалярное произведение перпендикулярных векторов равно нулю. Кроме того, из первого свойства следует геометрический смысл градиента – градиент это вектор, вдоль направления, которого производная по направлению наибольшая. Так как производная по направлению определяет тангенс угла наклона касательной к поверхности функции, то градиент направлен вдоль наибольшего наклона касательной.
Пример 2.

Вычислить
производную по направлению 
в точке A(2,3).
Решение.
Для вычисления производной по направлению
надо вычислить вектор градиента в
указанной точке и единичный вектор
направления  (т.е.
нормализовать вектор
(т.е.
нормализовать вектор  ).
).
Вектор градиента был вычислен в примере 1:

Вычисляем единичный вектор направления:

Вычисляем производную по направлению:

#2. Максимум и минимум функции нескольких переменных.
Определение. Функция 
Имеет
максимум в точке  (т. е. при
(т. е. при  и
и  ),
если
),
если

для
всех точек  ,
достаточно близких к точке
,
достаточно близких к точке 
Определение. Совершенно аналогично говорят, что
функция 
Имеет
минимум в точке 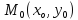 (т. е. при
(т. е. при  и
и 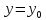 ),
если
),
если

для
всех точек  ,
достаточно близких к точке
,
достаточно близких к точке  и отличных от нее.
и отличных от нее.
Максимум и минимум функции называются экстремумами функции, т. е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.
Например, функция

Имеет очевидный минимум z = -1 при x = 1 и y = 2.

Функция

Имеет
максимум в точке 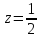 при x
= 0 и y
= 0.
при x
= 0 и y
= 0.

Теорема. (необходимые условия экстремума).
Если
функция 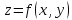 достигает экстремума при
достигает экстремума при  ,
, 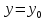 ,
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.
,
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.
Замечание. Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции. Можно привести примеры функций, которые в некоторых точках имеет нулевые частные производные, но не имеет экстремума в этих точка.
Пример. Функции, которая имеет нулевые частные производные, но не имеет экстремума.

В
точке  .
.
В самом деле:



Достаточные условия экстремума.
Теорема. Пусть в некоторой области, содержащей
точку 
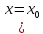 ,
,  функция
функция  имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка
имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка  является
критической точкой функции
является
критической точкой функции 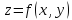 ,
т.е.
,
т.е.
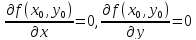
Тогда
при 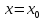 ,
, 
 имеет максимум,
если
имеет максимум,
если

 имеет минимум,
если
имеет минимум,
если

 не имеет ни
минимума, ни максимума, если
не имеет ни
минимума, ни максимума, если
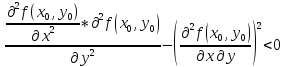
 может иметь
экстремум, а может и не иметь — требуется
дополнительное исследование, если
может иметь
экстремум, а может и не иметь — требуется
дополнительное исследование, если

Пример 3.2. Исследовать на максимум и на минимум функцию

Решение.
Найдем критические точки, т.е. точки, в которых первые частные производные равны нулю или не существуют.
Сначала вычисляем сами частные производные.


Приравниваем частные производные нулю и решаем следующую систему линейных уравнений

 = 0
= 0
Умножаем второе уравнение на 2 и складываем с первым. Получится уравнение только от y.

Находим  и подставляем
в первое уравнение
и подставляем
в первое уравнение

Преобразуем

Находим 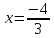
Следовательно,
точка ( )
является критической.
)
является критической.
Вычислим вторые производные второго порядка и подставим в них координаты критической точки.
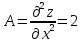


В нашем случае, подставлять значения критических точек не надо, так как вторые производные являются числами.
В итоге имеем:
Следовательно, найденная критическая точка, является точкой экстремума. Более того, так как

то эта точка минимума.
| Основные функции
модуль x: abs(x)
| 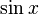 : sin[x] или Sin[x] : sin[x] или Sin[x]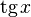 : tan[x] или Tan[x] : tan[x] или Tan[x] : cot[x] или Cot[x] : cot[x] или Cot[x]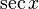 : sec[x] или Sec[x] : sec[x] или Sec[x]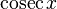 : csc[x] или Csc[x] : csc[x] или Csc[x]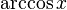 : ArcCos[x] : ArcCos[x]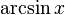 : ArcSin[x] : ArcSin[x]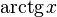 : ArcTan[x] : ArcTan[x]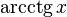 : ArcCot[x] : ArcCot[x]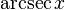 : ArcSec[x] : ArcSec[x]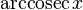 : ArcCsc[x] : ArcCsc[x]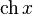 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 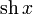 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]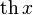 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]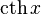 : coth[x] или Coth[x] : coth[x] или Coth[x] : sech[x] или Sech[x] : sech[x] или Sech[x]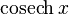 : csch[x] или Csch[е] : csch[x] или Csch[е] : ArcCosh[x] : ArcCosh[x] : ArcSinh[x] : ArcSinh[x] : ArcTanh[x] : ArcTanh[x] : ArcCoth[x] : ArcCoth[x] : ArcSech[x] : ArcSech[x]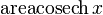 : ArcCsch[x] : ArcCsch[x] |
L_12gradient
4
Скалярные и векторные поля.
Определение 1. Скалярным полем точки М называется
скалярная функция  точки М вместе с областью ее определения.
точки М вместе с областью ее определения.
В пространственной
системе координат Oxyz
для каждой точки с координатами  ,
скалярное поле является функцией этих
координат:
,
скалярное поле является функцией этих
координат:  .
.
Примерами скалярных полей являются поле температуры атмосферы, поле плотности массы и т.д.
В дальнейшем будем предполагать, что скалярные поля являются однозначными, непрерывными и дифференцируемыми достаточное число раз.
Если частные
производные одновременно не равны нулю,
то уравнение 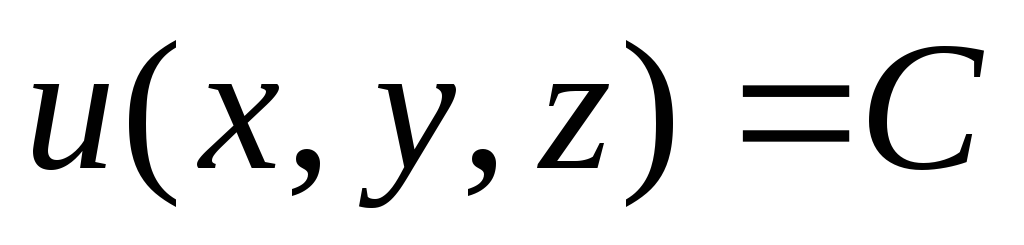 (С= const)
определяет поверхность, вдоль которой
функция
(С= const)
определяет поверхность, вдоль которой
функция  сохраняет постоянное значение; такая
поверхность называется поверхностью
уровня функции
сохраняет постоянное значение; такая
поверхность называется поверхностью
уровня функции  .
Очевидно, что рассматриваемая область
Т заполнена поверхностями уровня и
через каждую точку проходит одна и
только одна такая поверхность. Очевидно
также, что поверхности уровня не
пересекаются между собой. Аналогично
определяются линии уровня
.
Очевидно, что рассматриваемая область
Т заполнена поверхностями уровня и
через каждую точку проходит одна и
только одна такая поверхность. Очевидно
также, что поверхности уровня не
пересекаются между собой. Аналогично
определяются линии уровня  непрерывно дифференцируемой функции
непрерывно дифференцируемой функции  ,
заданной в области
,
заданной в области  .
.
Аналогично
определяются линии уровня  непрерывно дифференцируемой функции
непрерывно дифференцируемой функции  ,
заданной в области
,
заданной в области  .
.
Производная по направлению
Рассмотрим единичный
вектор  произвольного направления, где
произвольного направления, где  — углы, образуемые вектором
— углы, образуемые вектором  с осями координат.
с осями координат.
Параметрические
уравнения прямой , проходящей через
точку  в направлении вектора
в направлении вектора 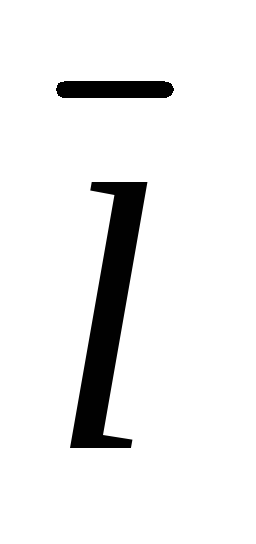 ,
имеют вид
,
имеют вид
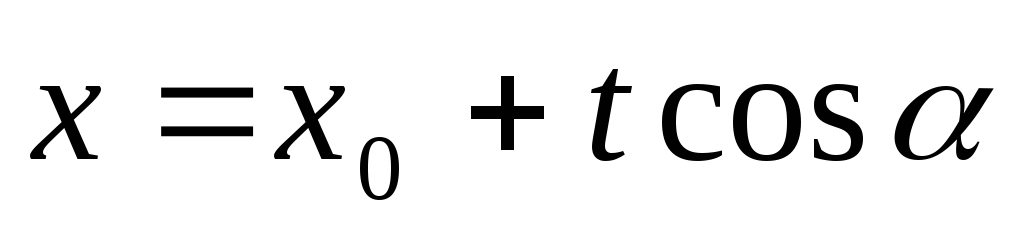 ,
,
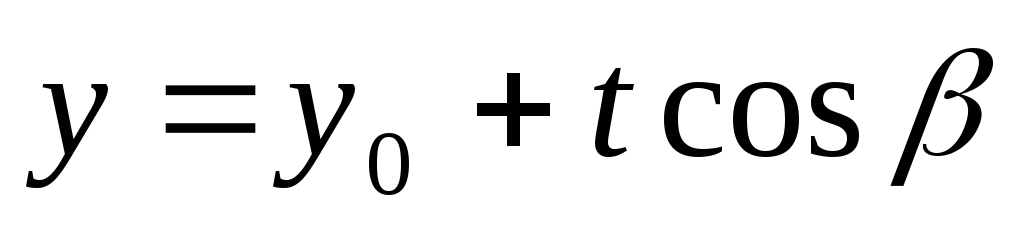 ,
(1)
,
(1)
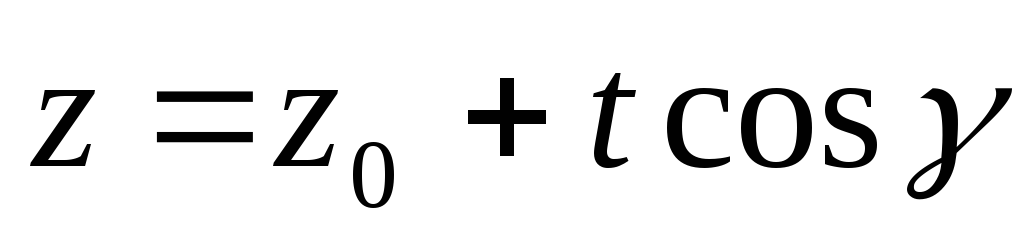 .
.
Тогда для точек
этой прямой функция  является функцией
является функцией  одной переменной
одной переменной 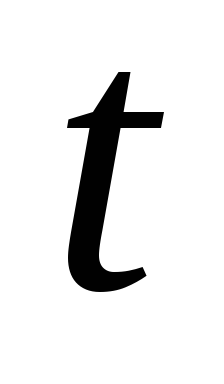 :
:
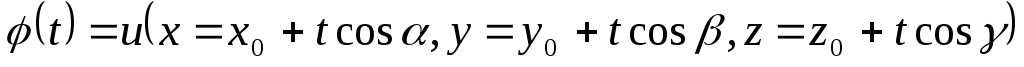 (2)
(2)
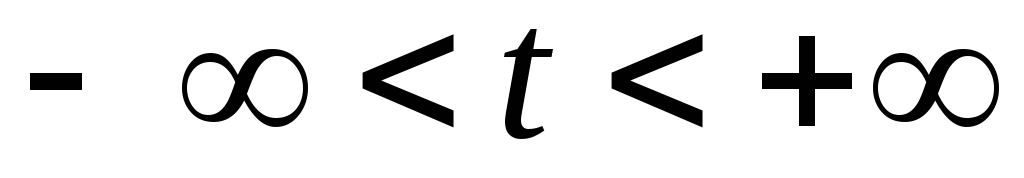
Определение 3. Производной
скалярного поля  в точке
в точке 
 по направлению
по направлению  называется производная функции
называется производная функции  по
по  при
при  ,
если она существует, и обозначается
,
если она существует, и обозначается  .
.
Можно сказать, что
производная по направлению  есть скорость изменения скалярного
поля по отношению к величине перемещения
точки М вдоль выбранного направления.
есть скорость изменения скалярного
поля по отношению к величине перемещения
точки М вдоль выбранного направления.
Дифференцируя
правую часть равенства (2) по  ,
получаем
,
получаем
 (3)
(3)
где  — направляющие косинусы вектора
— направляющие косинусы вектора 
 .
.
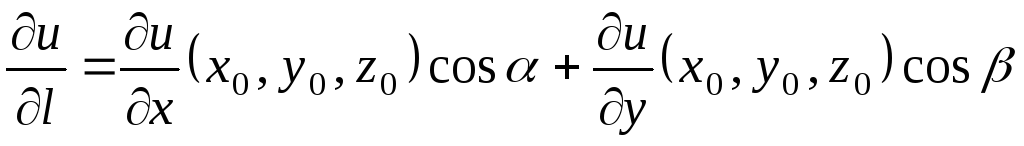
Пример 1. Вычислить производную функции  в точке
в точке  по направлению вектора
по направлению вектора  ,
где
,
где  .
.
Решение. Определим
единичный вектор  заданного направления
заданного направления 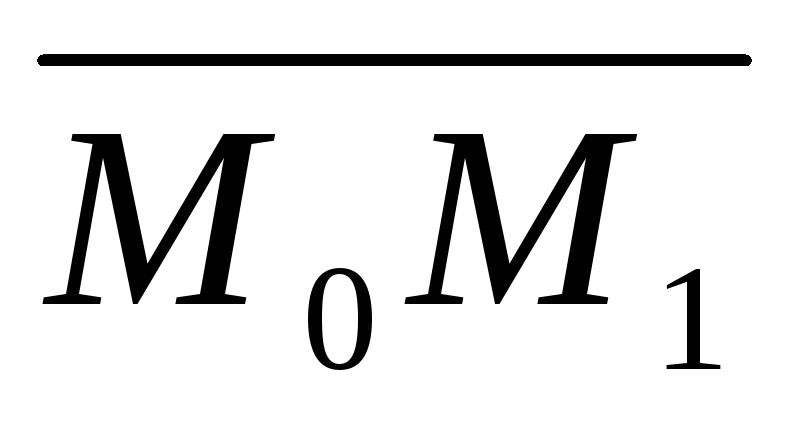 .
Имеем
.
Имеем  .
. 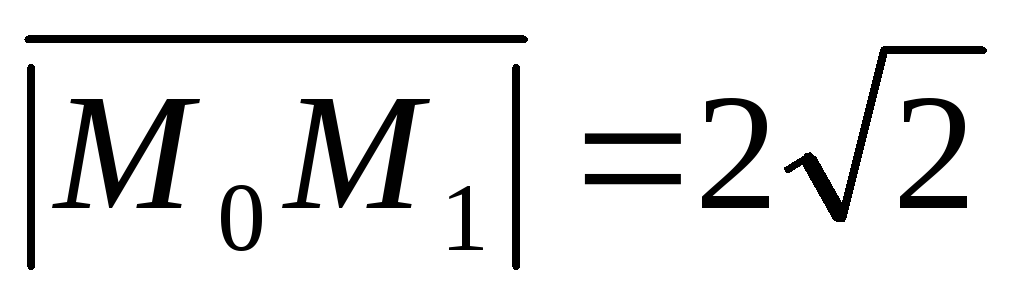 ,
,
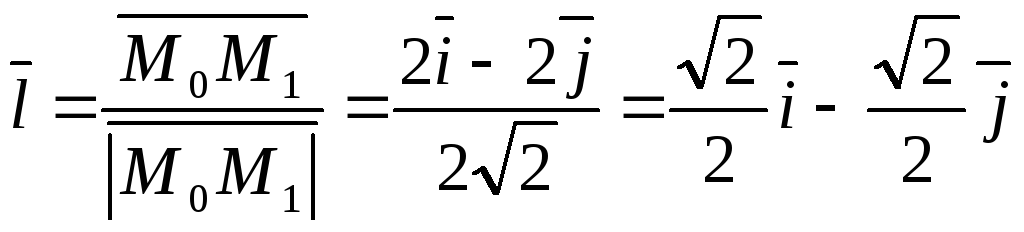 .
.
Отсюда 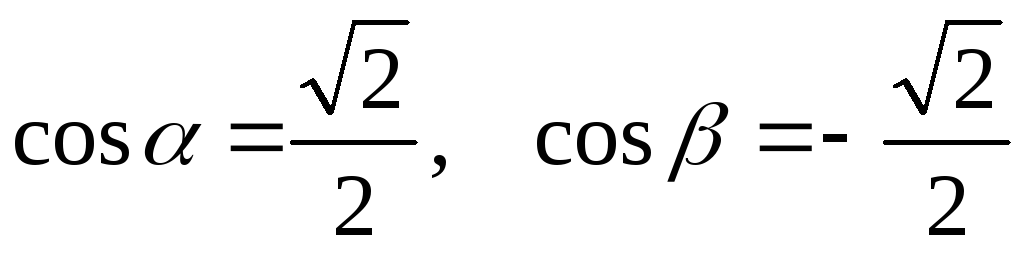 .
Найдем частные производные функции в
точке
.
Найдем частные производные функции в
точке  :
:
 ,
,
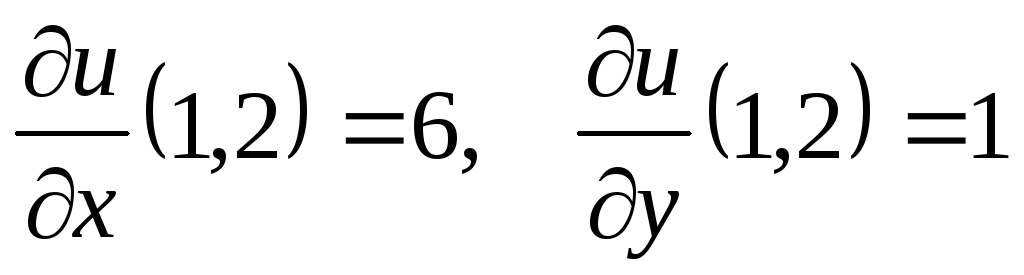 .
.
 .
.
3. Градиент
Определение 4. Градиентом
дифференцируемого скалярного поля 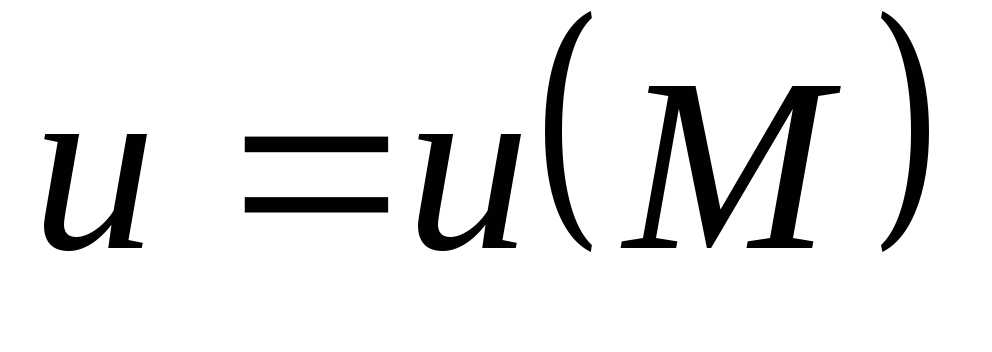 называется векторное поле точки М,
обозначаемое
называется векторное поле точки М,
обозначаемое  и определяемое формулой
и определяемое формулой
 (4)
(4)
Градиентами некоторых скалярных полей являются поле сил тяготения, поле заряда и т.д.
Пользуясь известными формулами для нахождения модуля вектора, получим
 ,
,
(5)
 ,
,  ,
, 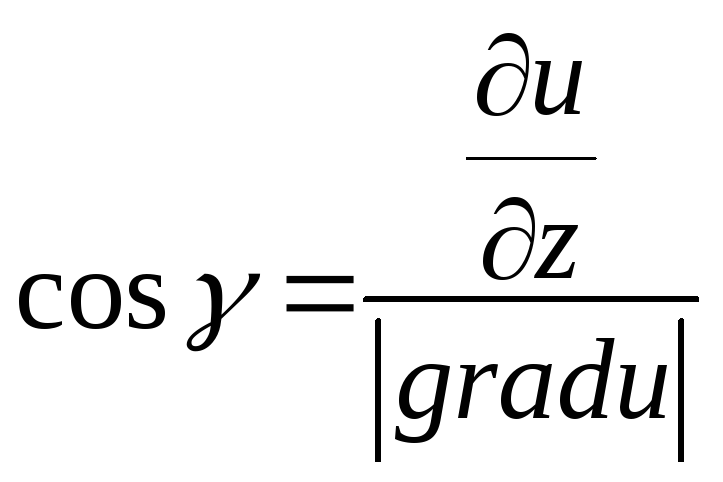 .
.
Используя понятие
градиента и формулу для скалярного
произведения, представим формулу (3) в
виде скалярного произведения векторов  и
и  :
:
 (6)
(6)
 (7)
(7)
Из (7) следует, что
в каждой точке, не являющейся особой,
градиент направлен в сторону максимального
возрастания функции, а модуль градиента
равен величине скорости этого возрастания.
Действительно. В случае 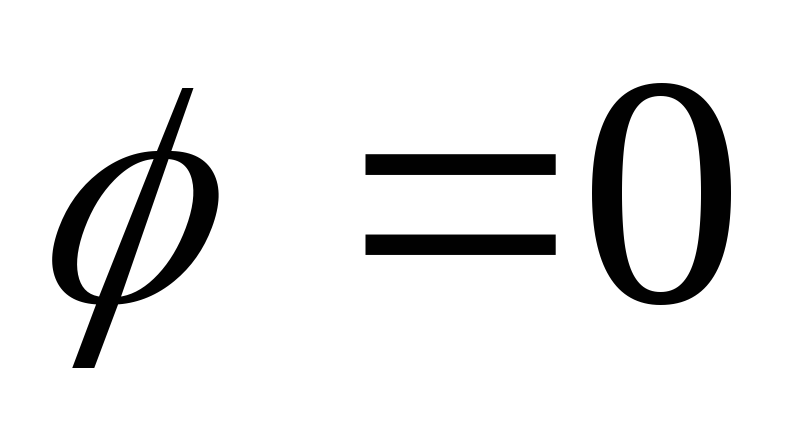 вектор
вектор  имеет то же направление, что и
имеет то же направление, что и 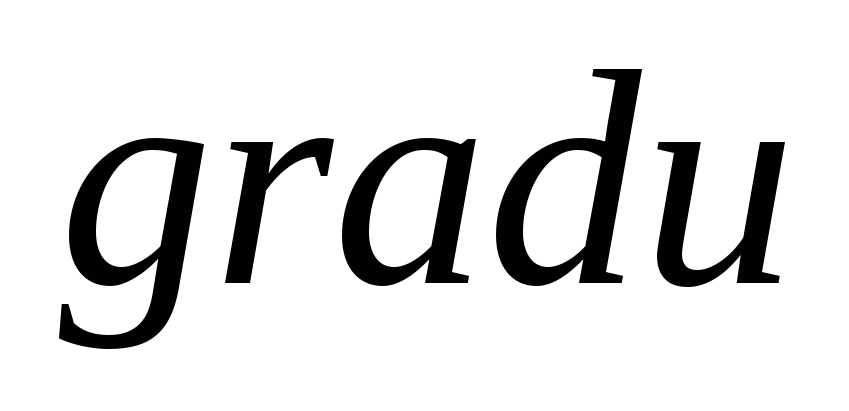 ,
и тогда
,
и тогда
 . (8)
. (8)
Формула (8) позволяет вместо предыдущего определения градиента, в котором используется система координат, дать другое, инвариантное определение.
Определение 5. Градиентом скалярного поля  называется вектор, характеризующий
наибольшую (по модулю и направлению)
скорость изменения этого скалярного
поля.
называется вектор, характеризующий
наибольшую (по модулю и направлению)
скорость изменения этого скалярного
поля.
Это определение градиента инвариантно, т.е. не зависит от выбора системы координат.
Если  ,
то производная по направлению является
наименьшей, равной
,
то производная по направлению является
наименьшей, равной  .
Если же
.
Если же 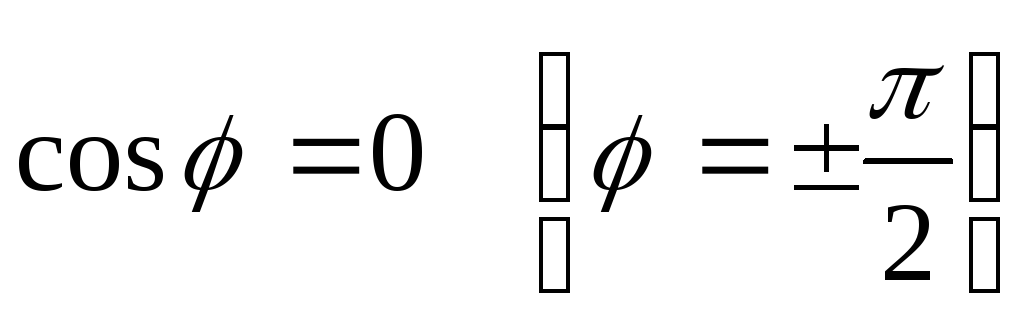 ,
то производная по направлению равна
нулю. Направление градиента совпадает
с направлением нормали к поверхности
уровня
,
то производная по направлению равна
нулю. Направление градиента совпадает
с направлением нормали к поверхности
уровня  .
.
Пример 2. Найти градиент скалярного поля 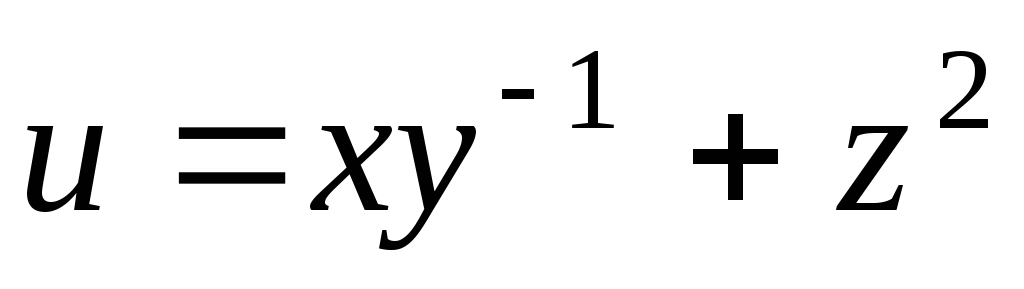 в точке
в точке  .
Вычислить его величину и направление.
.
Вычислить его величину и направление.
Решение: Имеем  ,
,  ,
Следовательно
,
Следовательно 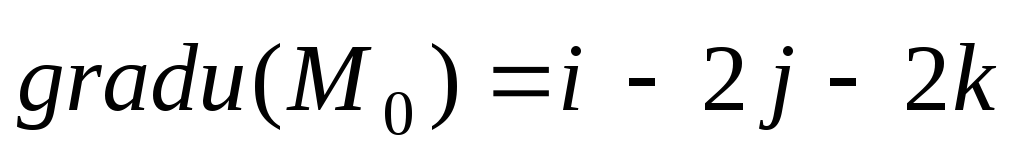 ;
;  ;
;  ,
,  ,
,  .
.
3.2. Градиент функции | Решение задач по математике и другим предметам!!
При изучении скалярных полей наряду с функций рассматривается некоторый вектор, тесно связанный с этой функцией, — градиент скалярного поля.
Градиентом в точке скалярного поля, заданного дифференцируемой функцией , называется вектор, равный
.
Таким образом, каждой точке скалярного поля, заданного дифференцируемой функцией , соответствует не только значение этой функции, но и вполне определенный вектор .
Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.
Теорема. Проекция вектора На единичный вектор равна производной функции по направлению :
.
Доказательство. Пусть . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.
Так как , , то
.
Учитывая, что производная по направлению выражает скорость изменения скалярного поля в этом направлении, можно сказать, что проекция на вектор равна скорости изменения поля в направлении вектора .
Обозначим через угол между единичным вектором и . Тогда .
Поэтому .
Если направления векторов и совпадают (), то производная по направлению имеет, очевидно, наибольшее значение, равное .
Таким образом, есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.
Рассмотрим кривую , лежащую на поверхности уровня и проходящую через точку . Градиент функции в точке обладает следующими свойствами: перпендикулярен к вектору , направленному по касательной к кривой в точке .
В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных , градиент определяется формулой
.
Его связь с производной по направлению выражается равенством
,
Где — угол между единичным вектором и . Вектор перпендикулярен к касательной, проведенной к линии уровня в точке .
Пример 16. Найти наибольшую скорость возрастания функции
в точке .
Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции :
,
.
В точке имеем .
Тогда наибольшая скорость возрастания функции равна
.
Пример 17. Найти скорость изменения скалярного поля, определяемого функцией в точке в направлении касательной, проведенной к параболе в этой точке в сторону возрастания координаты , и наибольшую скорость изменения поля в этой точке.
Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля по направлению вектора , задающего направление.
,
Где ; — направляющие косинусы вектора , . Вектор возьмем на касательной к параболе в , для чего составим уравнение касательной
,
,
— уравнение касательной.
На найденной касательной возьмем точку с любой координатой (), например . Тогда
.
Найдем значения производной по направлению в точке :
,
.
Тогда .
Наибольшая скорость изменения поля в точке есть .
Так как , то
.
Величина наибольшей скорости
.
| < Предыдущая | Следующая > |
|---|
Градиент | Наука | Fandom
Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.
Градиент (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, показывающий направление наискорейшего возрастания некоторой величины $ \varphi $, значение которой меняется от одной точки пространства к другой (скалярного поля). Например, если взять в качестве $ \varphi $ высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма». Величина (модуль) вектора градиента равна скорости роста $ \varphi $ в этом направлении.
Термин впервые появился в метеорологии, а в математику был введен Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Для случая трёхмерного пространства, градиентом называется векторная функция с компонентами $ \frac {\partial \varphi} {\partial x} $, $ \frac {\partial \varphi} {\partial y} $, $ \frac {\partial \varphi} {\partial z} $, где $ \varphi $ — некоторая скалярная функция координат $ x $, $ y $, $ z $.
Если $ \varphi $ — функция $ n $ переменных $ x_1,\;\ldots,\;x_n $, то её градиентом называется $ n $-мерный вектор
- $ \left(\frac{\partial \varphi}{\partial x_1},\;\ldots,\;\frac{\partial \varphi}{\partial x_n}\right), $
компоненты которого равны частным производным $ \varphi $ по всем её аргументам.
Градиент обозначается $ \mathrm{grad}\,\varphi $ или, с использованием оператора набла, $ \nabla \varphi $.
Из определения градиента следует, что:
$ \mathrm{grad}\,\varphi = \nabla \varphi = \frac {\partial \varphi} {\partial x} \vec e_x + \frac {\partial \varphi} {\partial y} \vec e_y + \frac {\partial \varphi} {\partial z} \vec e_z. $
Смысл градиента любой скалярной функции $ f $ в том, что его скалярное произведение с бесконечно малым вектором перемещения $ d\mathbf{x} $ дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена $ f $, то есть линейную (в случае общего положения она же главная) часть изменения $ f $ при смещении на $ d\mathbf{x} $. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
$ df = \frac {\partial f} {\partial x_1}\,dx_1 + \frac {\partial f} {\partial x_2}\,dx_2 + \frac {\partial f} {\partial x_3}\,dx_3 + \ldots = \sum_i \frac {\partial f} {\partial x_i}\,dx_i = (\mathrm{grad}\,\mathbf{f} \cdot d\mathbf x). $
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат $ x_i $, то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку $ d\mathbf{x} $ — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:
$ d f = \sum_i (\partial_i f)\,dx^i $
или, опуская по правилу Эйнштейна знак суммы,
$ df=(\partial_i f)\,dx^i $
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Например, градиент функции $ \varphi(x,\;y,\;z)=2x+3y^2-\sin z $ будет представлять собой:
- $ \nabla \varphi = \left(\frac{\partial \varphi}{\partial x},\;\frac{\partial \varphi}{\partial y},\;\frac{\partial \varphi}{\partial z}\right)=(2,\;6y,\;-\cos z) $
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по направлению температуры среды и т. д. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
Геометрический смысл Править
Рассмотрим семейство линий уровня функции $ \varphi $:
- $ \gamma(h)=\{(x_1,\;\ldots,\;x_n)\mid \varphi(x_1,\;\ldots,\;x_n)=h\}. $
Нетрудно показать, что градиент функции $ \varphi $ в точке $ \vec{x}{\,}^0 $ перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности $ \vec{x}{\,}^0 $, то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъема в данной точке.
Связь с производной по направлению Править
Используя
II Градиент
Определение
2.Вектор, проекциями которого служат
частные производные функции ,
называется градиентом функции
,
называется градиентом функции
 .
.
Для
функции трёх переменных  :
:
 .
.
Связь градиента с производной по направлению даётся следующей теоремой.
Теорема 2.Производная функции по направлению есть проекция её градиента на это направление:
 .
.
Доказательство.Проекция вектора на ось – это проекция вектора на орт оси. Проекцию же вектора на вектор можно найти, используя скалярное произведение:
 .
.
Учитывая, что  и
и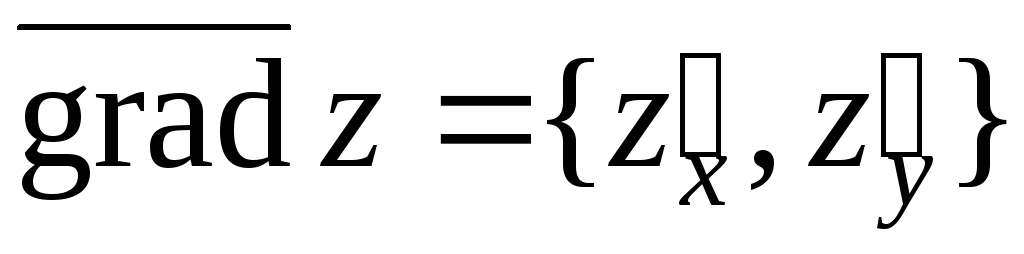 ,
причём
,
причём ,
получим:
,
получим:
 .
.
Правая часть этого равенства в силу Теоремы 1 есть производная по направле-нию. Теорема доказана.
Следствие 1.Производная функции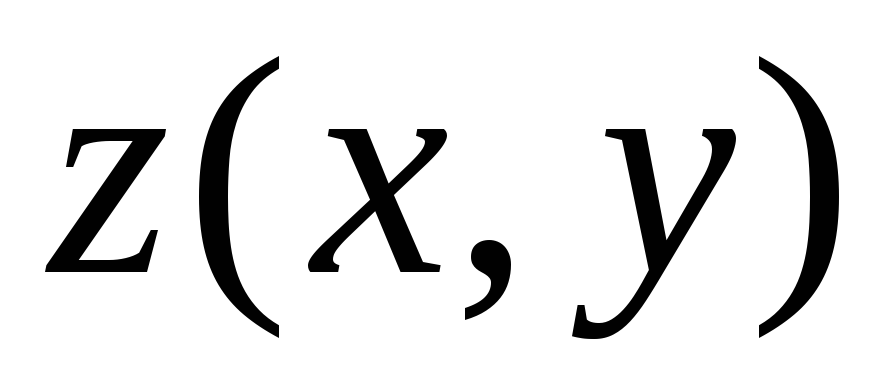 в точке
в точке по направлению оси
по направлению оси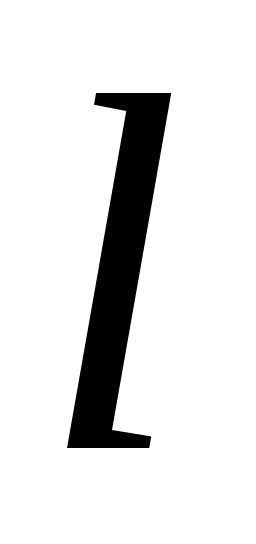 достигает максимума, когда это направление
совпадает с градиентом функции, причём
достигает максимума, когда это направление
совпадает с градиентом функции, причём
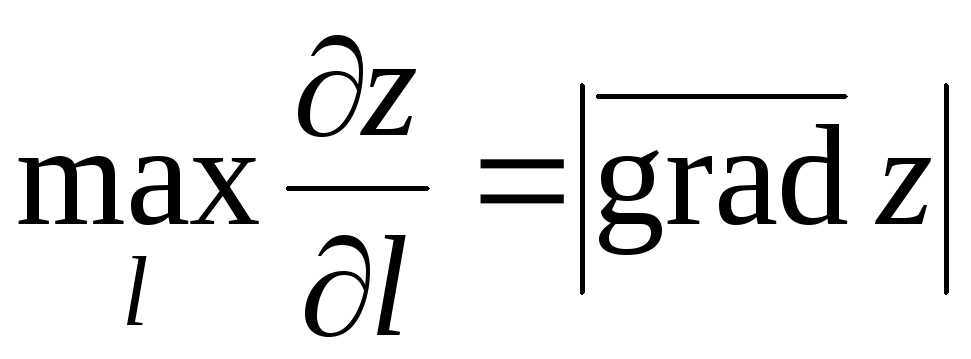 .
.
Таким образом, градиент функции в данной точке характеризует направление и величину максимальной скорости возрастания функции в данной точке.
Следствие 2.Производная функции по направлению, перпендикулярному её градиенту, равна нулю.
III Линии и поверхности уровня
Очень часто, чтобы
яснее представить себе график функции 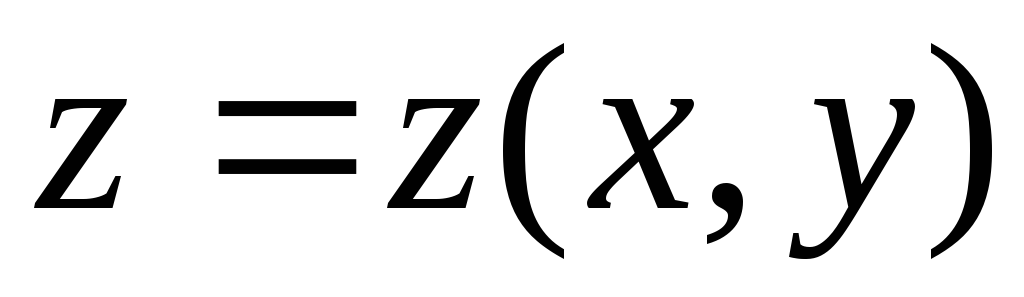 (т.е. некоторую поверхность) используют
т.н. линии уровня.
(т.е. некоторую поверхность) используют
т.н. линии уровня.
Определение
2.Линией уровня функции называют линию (в области определения
называют линию (в области определения ),
вдоль которой функция принимает
постоянное значение, т.е. линию, уравнение
которой имеет вид
),
вдоль которой функция принимает
постоянное значение, т.е. линию, уравнение
которой имеет вид ,
где
,
где – константа.
– константа.
Например, для
функции  ,
линии уровня – это два семейства (
,
линии уровня – это два семейства ( и
и )
сопряжённых гипербол, а так же биссектрисы
координатных углов (
)
сопряжённых гипербол, а так же биссектрисы
координатных углов (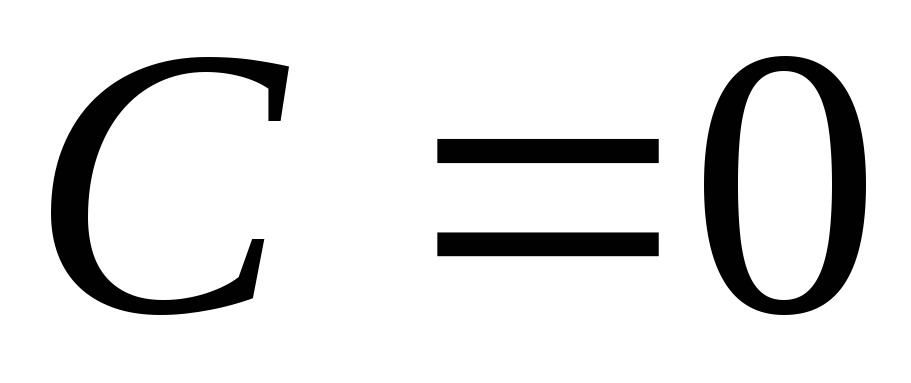 ).
).
Для функции трёх
переменных  аналогично вводится понятие поверхности
уровня, т.е. поверхности, определяемой
уравнением
аналогично вводится понятие поверхности
уровня, т.е. поверхности, определяемой
уравнением
 .
.
Следствие 3.Градиент функции в заданной точке перпендикулярен линии (поверхности) уровня функции, проходящей через эту точку, т.е. направлен по нормали к линии (поверхности) уровня.
Доказательство.(Для функции двух переменных). Рассмотрим
уравнение линии уровня функции :
:
 .
.
Это уравнение
определяет неявную функцию  и её производная имеет вид:
и её производная имеет вид: .
Уравнение нормали к графику
.
Уравнение нормали к графику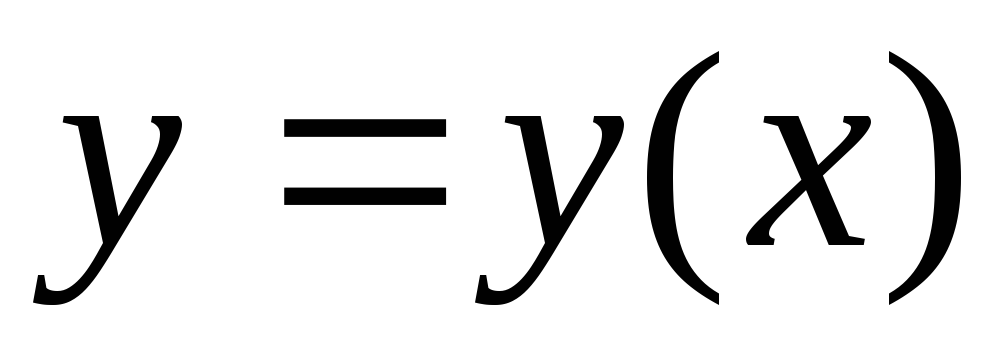 в точке
в точке :
:
 .
.
В нашем случае:  .
Это уравнение легко переписать в
канонической форме:
.
Это уравнение легко переписать в
канонической форме:
 .
.
Из которой следует,
что направляющий вектор нормали 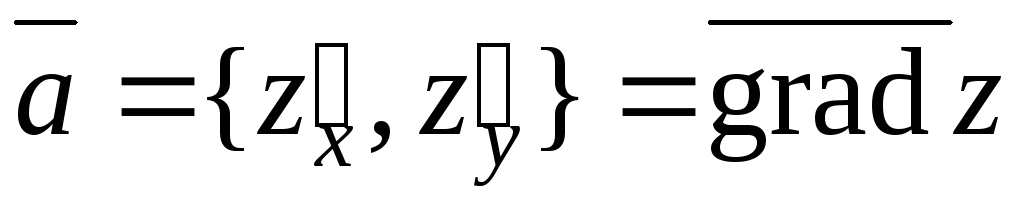 .
Это и означает, что градиент функции
направлен по нормали к линии уровня
этой функции.
.
Это и означает, что градиент функции
направлен по нормали к линии уровня
этой функции.
Пример.Для функции линии уровня :
линии уровня : – это семейство эллипсов
– это семейство эллипсов
 .
.
Проверим, что
семейство парабол  пересекает все эти эллипсы под прямым
углом. Дифференцируем уравнение эллипсов
по
пересекает все эти эллипсы под прямым
углом. Дифференцируем уравнение эллипсов
по :
:
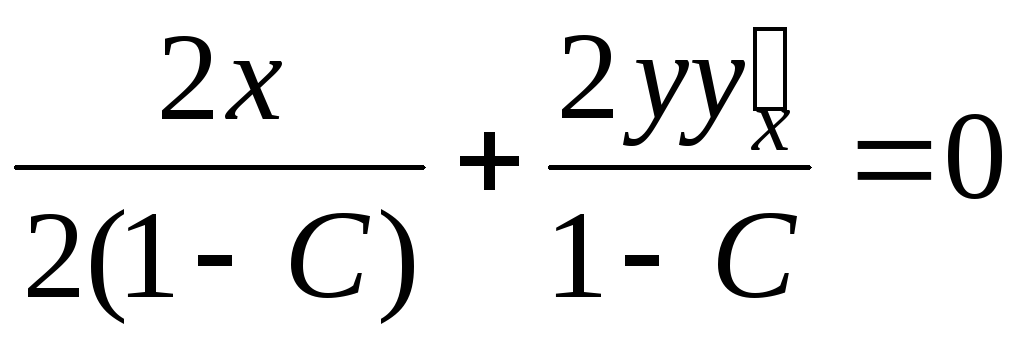
Отсюда угловой коэффициент касательной к эллипсу (в произвольной точке):
 .
.
Для параболы тот же коэффициент имеет вид:
 .
.
Пусть 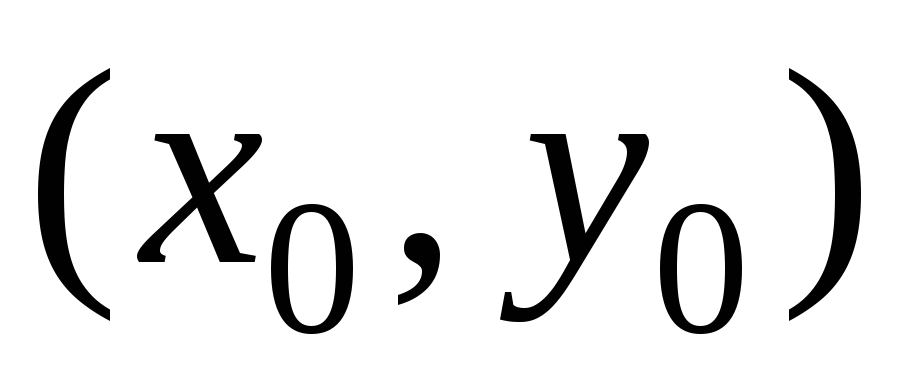 – точка пересечения какого-либо эллипса
с некоторой параболой. Тогда
– точка пересечения какого-либо эллипса
с некоторой параболой. Тогда и произведение угловых коэффициентов
касательных в этой точке:
и произведение угловых коэффициентов
касательных в этой точке:
 .
.
Отсюда следует,
что касательные перпендикулярны, т.е.
рассмотренные семейства
взаимно-перпендикулярны. Градиент
функции  в точке
в точке направлен по касательной к той параболе
из семейства
направлен по касательной к той параболе
из семейства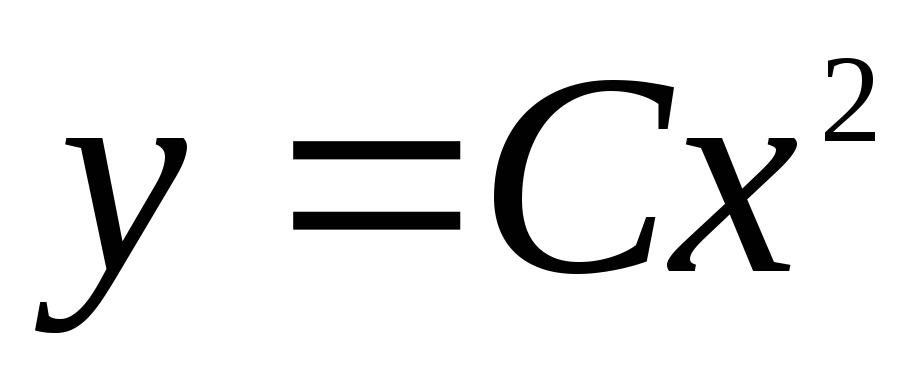 ,
которая проходит через
,
которая проходит через ,
причём в сторону вершины параболы, ибо
начало координат – это абсолютный
максимум данной функции.
,
причём в сторону вершины параболы, ибо
начало координат – это абсолютный
максимум данной функции.
Одна интерпретация
полученного результата. Поверхность,
определяемая рассмотренной функции, –
это эллиптический параболоид с вершиной
в точке 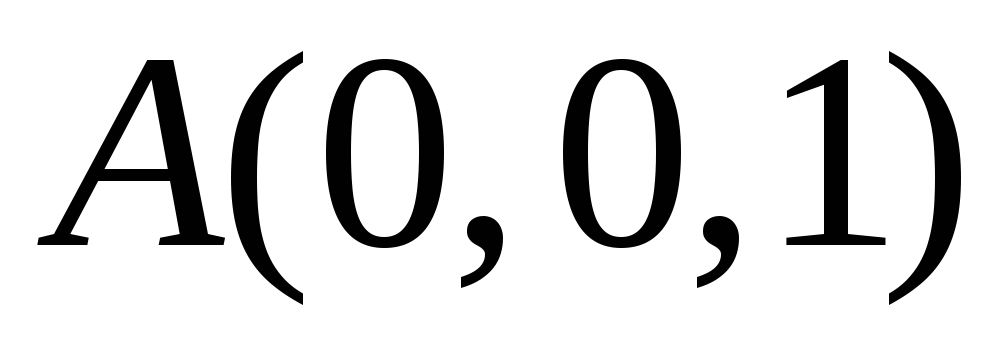 ,
расположенный ниже плоскости
,
расположенный ниже плоскости .
Потоки воды с такой поверхности стекают
по траекториям, проекциями которых
служат параболы семейства
.
Потоки воды с такой поверхности стекают
по траекториям, проекциями которых
служат параболы семейства .
.


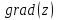 равна нулю.
равна нулю. имеет максимум,
если
имеет максимум,
если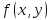 имеет минимум,
если
имеет минимум,
если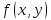 не имеет ни
минимума, ни максимума, если
не имеет ни
минимума, ни максимума, если может иметь
экстремум, а может и не иметь — требуется
дополнительное исследование, если
может иметь
экстремум, а может и не иметь — требуется
дополнительное исследование, если
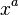 : x^a
: x^a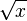 : Sqrt[x]
: Sqrt[x]![\sqrt[n]{x}](/800/600/https/upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n)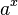 : a^x
: a^x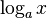 : Log[a, x]
: Log[a, x]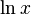 : Log[x]
: Log[x]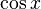 : cos[x] или Cos[x]
: cos[x] или Cos[x]