Высота длина широта – в какой последовательности правильно писать ширину высоту глубину и как правильно пишиться, наведите пример например

Измерение расстояний с помощью градусной сетки — урок. География, 5 класс.

С помощью градусной сетки на географической карте и глобусе можно определять расстояния. Все меридианы — одинаковой длины, поэтому известно, что длины их дуг величиной \(1°\) составляют \(111,3\) км.

Длины дуг величиной \(1°\) для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. Для расчётов используют таблицу значений длин дуг \(1°\) параллелей для разных широт:

Определение расстояний по параллели

Длины дуг величиной \(1°\) для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам.

\(А =\) (\(д1\)\(+\) \(д2\)) \(·\) \(104,6\) (длина \(1°\) на широте \(20°\)) \(=\) (\(10° +\) \(20°\)) \(·\) \(104,6 =\) \(30°\) \(·\) \(104,6 =\) \(3 138\) км.

\(Б =\) (\(д1\) \(–\) \(д2\)) \(·\) \(109,6 =\) (\(20° –\) \(10°\)) \(·\) \(109,6 =\) \(10° ·\) \(109,6 =\) \(1 096\) км.

\(В =\) (\(д2\) \(–\) \(д1\)) \(·\) \(96,5 =\) (\(90° –\) \(60°\)) \(·\) \(96,5 =\) \(30° ·\) \(96,5 =\) \(2 895\) км.

Определение расстояний по меридиану

Длина дуги \(1°\) меридиана приблизительно равна \(111,3\) км (\(20 000\) км \(:\) \(180° =\) \(111,3\) км).

\(А =\) (\(ш1\)\(+\) \(ш2\)) \(·\) \(111,3 =\) (\(20° +\) \(10°\)) \(·\) \(111,3 =\) \(30° ·\) \(111,3 =\) \(3 339\) км.

\(Б =\) (\(ш1\) \(–\) \(ш2\)) \(·\) \(111,3 =\) (\(40° –\) \(10°\)) \(·\) \(111,3 =\) \(30° ·\) \(111,3 =\) \(3 339\) км.

\(В =\) (\(ш2\) \(–\) \(ш1\)) \(·\) \(111,3 =\) (\(30° –\) \(10°\)) \(·\) \(111,3 =\) \(20° ·\) \(111,3 =\) \(2 226\) км.

Высота (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.

Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.

Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:

EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}

(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)

Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.

2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.

3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.

Конспект «Градусная сеть. Координаты» — УчительPRO

Градусная сеть. Географические координаты

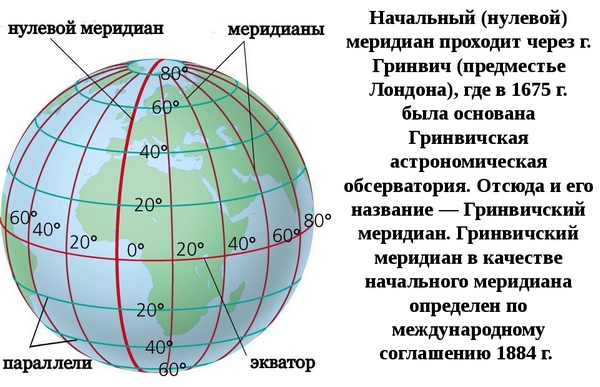
Градусная сеть Земли – система меридианов и параллелей на географических картах и глобусах, служащая для отсчета географических координат точек земной поверхности – долгот и широт – или нанесения на карту объектов по их координатам.

Для создания градусной сети необходимы определенные точки отсчета. Шарообразная форма Земли определяет существование на земной поверхности двух неподвижных точек – полюсов. Через полюсы проходит воображаемая ось, вокруг которой вращается Земля.

 Основные элементы градусной сетки карты — по­люсы, экватор, меридианы и параллели.

Географические полюсы – математически высчитанные точки пересечения воображаемой оси вращения Земли с земной поверхностью.

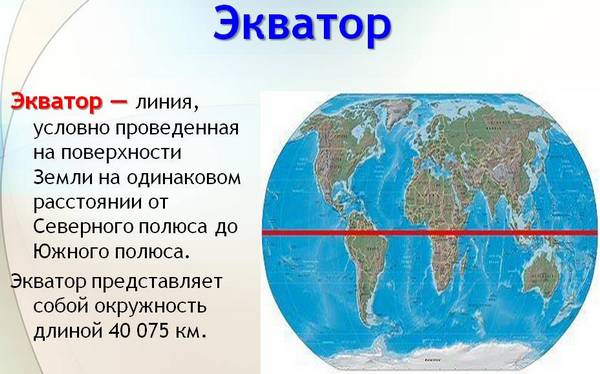
Экватор – воображаемая линия на земной поверхности, полученная при мысленном рассечении эллипсоида на две равные части (Северное и Южное полушарие).

Все точки экватора равноудалены от полюсов. Плоскость экватора перпендикулярна оси вращения Земли и проходит через ее центр. Полушария мысленно разделены еще множеством плоскостей, параллельных плоскости экватора.

Линии их пересечения с поверхностью эллипсоида называются параллелями .

Все они, как и плоскость экватора, перпендикулярны оси вращения планеты. Параллелей на карте и глобусе можно провести сколько угодно, но обычно на учебных картах их проводят с интервалом 10—20°. Параллели всегда ориентированы с запада на восток. Длина окружности параллелей уменьшается от экватора к полюсам. На экваторе она самая большая, а на полюсах равна нулю.

При пересечении земного шара воображаемыми плоскостями, проходящими через ось Земли перпендикулярно плоскости экватора, образуются большие окружности – меридианы .

Меридианы также можно провести через любые точки эллипсоида. Все они пересекаются в точках полюсов. Меридианы ориентированы с севера на юг. Средняя длина дуги 1° меридиана: 40 008,5 км : 360° = 111 км. Длина всех меридианов одинакова. Направление местного меридиана в любой точке можно определить в полдень по тени от любого предмета. В Северном полушарии конец тени всегда показывает направление на север, в Южном – на юг.

Градусная сеть необходима для отсчета географических координат точек земной поверхности – широты и долготы.

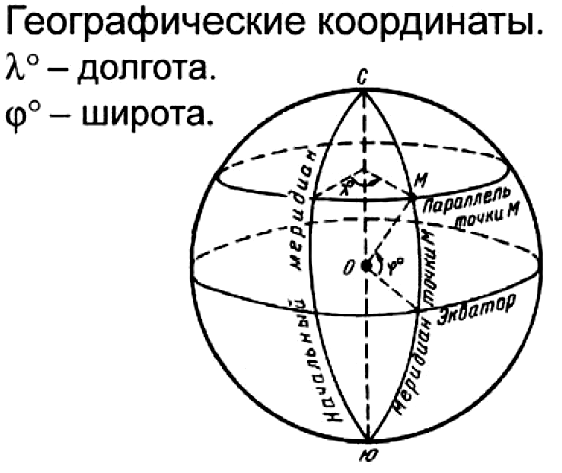
Географические координаты.

Географические координаты — это географическая широта и долгота.

Географическая широта – расстояние вдоль меридиана в градусах от экватора до какой-либо точки на поверхности Земли.

Началом отсчета является экватор. Широта всех точек на нем равна 0. На полюсах широта составляет 90°. К северу от экватора отсчитывают северную широту, к югу – южную.

Географическая долгота – расстояние вдоль параллели в градусах от начального меридиана до какой-либо точки земной поверхности.

Все меридианы равны по длине, поэтому для отсчета необходимо было выбрать один из них. Им стал Гринвичский меридиан, проходящий недалеко от Лондона (там, где расположена Гринвичская обсерватория). Долгота отсчитывается от 0° до 180°. К востоку от нулевого меридиана до 180° отсчитывается восточная долгота, к западу – западная. Таким образом, используя градусную сеть, можно точно определить географические координаты – величины, определяющие положение точки на земной поверхности относительно экватора и нулевого меридиана.

Например, географические координаты мыса Челюскин (крайней северной точки Евразии) – 78° с. ш. и 104° в. д.

Глобус

Глобус (от лат. globus, «шар») — это обобщенная модель Земли [или другой планеты, а также модель небесной сферы (небесный глобус)], приведённая из её реальной формы к упрощенной и уменьшенной форме сферы. Обычно на глобусах в уменьшенном виде изображают поверхность Земли: очертания суши и водных объектов, рельеф материков и дна Мирового океана, реки, а также границы государств, города.

Глобус наиболее точно отражает облик Земли. Глобус обладает целым рядом геометрических свойств:

• равномасштабность изображения — любой отрезок линии на поверхности земного шара изображается на глобусе с одинаковым уменьшением, т. е. его масштаб всюду постоянен;
• равноугольность — горизонтальные углы, измеренные на земной поверхности, равны соответствующим углам на глобусе, а изображение любого географического объекта на глобусе подобно его действительным очертаниям на местности;
• равновеликость — глобус сохраняет правильное соотношение площадей.

На глобусе правильно переданы очертания, размеры, взаимное расположение материков и океанов. Есть и другие отличия глобуса от географической карты.

---

Закрепить теорию практикой !

(пройти тесты с проверкой ответа сразу и объяснением правильного ответа)

тренажер: Географическая координаты. Высоты и глубины.

---

 

Следующая тема: Масштаб. Определение расстояний

 

Длина — это… Что такое Длина?

Длина

Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине). В физике термин «длина» обычно используется как синоним «расстояния» и обозначается или .

Размерность длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из фундаментальных единиц измерения, на основе которых образуются другие единицы. В международной системе единиц (СИ) за единицу длины принят метр.

Единицы измерения длины

Относительные размеры
объектов, м.

-20 —

–

-18 —

–

-16 —

–

-14 —

–

-12 —

–

-10 —

–

-8 —

–

-6 —

–

-4 —

–

-2 —

–

0 —

–

2 —

–

4 —

–

6 —

–

8 —

–

10 —

–

12 —

–

14 —

–

16 —

–

18 —

–

20 —

–

22 —

–

24 —

–

26 —

–

28 —

–

30 —

Метрическая система

Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Париже. Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.

Британская/Американская система

Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.

Старорусская система

В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие^[1].

В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.

[2]

См. также

Древнегреческая система

Мусульманская система

• Ангушт или Асба (аналог дюйма)
• Пай (аналог фута)
• Ба или кама, равная приблизительно 2 м
• Касаба или наб
• Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
• Барид, равный четырём фарсахам^[3]

Типографическая система

Морская система

Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Ее численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.

Международная морская миля составляет 1852 м, в отличие от морской мили Британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м).^[4]

Единицы, применяемые в астрономии

Измерительные инструменты и меры

Измерительные приборы

Другие средства

• Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
• Очень маленькие расстояния измеряются с помощью измерительных микроскопов

См. также

Примечания

Категории:

• Физические величины по алфавиту
• Метрология

Wikimedia Foundation. 2010.

высокие широты — это… Что такое высокие широты?



высокие широты

high latitudes

Большой англо-русский и русско-английский словарь. 2001.

• высокие частоты
• высокий

Смотреть что такое «высокие широты» в других словарях:

• высокие широты — Условное название приполярных областей земного шара, ограниченных примерно 65° северной и южной широты …   Словарь по географии

• Высокие широты — (high latitudes)High latitudes, термин, которым часто называют околополюсные широты к С. и Ю. от 60о …   Страны мира. Словарь

• Климат — (от греч. klíma, родительный падеж klímatos, буквально наклон; подразумевается наклон земной поверхности к солнечным лучам)         многолетний режим погоды, свойственный той или иной местности на Земле и являющийся одной из ее географических… …   Большая советская энциклопедия

• Земля (планета) — Земля (от общеславянского зем пол, низ), третья по порядку от Солнца планета Солнечной системы, астрономический знак Å или, ♀. I. Введение З. занимает пятое место по размеру и массе среди больших планет, но из планет т. н. земной группы, в… …   Большая советская энциклопедия

• Земля — I Земля (от общеславянского зем пол, низ)         третья по порядку от Солнца планета Солнечной системы, астрономический знак ⊕ или, ♀.          I. Введение          З. занимает пятое место по размеру и массе среди больших планет, но из планет т …   Большая советская энциклопедия

• Климат — (греч. κλίμα, κλίματος означает наклон солнца, иначе сказать, полуденную высоту солнца). Древние географы делили Землю на климатические пояса в зависимости от этого явления и длины дня, принимая в расчет так называемые астрономические климаты,… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• климат — а; м. [от греч. klima (klimatos) наклон (солнечных лучей)] 1. Многолетний режим погоды, свойственный той или иной местности на Земле и являющийся одной из её географических характеристик. Изменение климата. Жаркий, умеренный, континентальный,… …   Энциклопедический словарь

• Арктика — сев. полярная обл. Земли. Название от греч. арктикос северный, полярный из греч. арктос медведь сев. полярная обл. находится непосредственно под созвездием Большой Медведицы. Географические названия мира: Топонимический словарь. М: АСТ. Поспелов… …   Географическая энциклопедия

• Узкозубая акула — Научная класс …   Википедия

• КООРДИНАТНАЯ СЕТКА — в топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора большой окружности,… …   Энциклопедия Кольера

• координатная сетка — в топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора – большой окружности,… …   Географическая энциклопедия

Книги

• Высокие широты. 100 фотографий, Хворостов Сергей Николаевич. «Высокие широты. 100 фотографий»-книга посвящена Арктике и Антарктике, экстремальным экспедициям, обитателям полярных широт и всем тем, кто связал свою жизнь с полюсами. Есть на Земле такие… Подробнее  Купить за 1771 руб
• Высокие широты. 100 фотографий, Хворостов С.. «Высокие широты. 100 фотографий»-книга посвящена Арктике и Антарктике, экстремальным экспедициям, обитателям полярных широт и всем тем, кто связал свою жизнь с полюсами. Есть на Земле такие… Подробнее  Купить за 1450 руб
• Высокие широты, Образцов П.А.. Книга повествует об открытии и освоении Арктики и Антарктики, этих двух полюсов холода и мужества, об отважных героях, благодаря которым человечество узнало о природе, животном мире самых… Подробнее  Купить за 591 руб

Другие книги по запросу «высокие широты» >>