Js битовые операции: Побитовые операторы

javascript — Побитовый сдвиг влево, проблемка

Переписываю некий код с яваскрипта на пхп, должен работать идентично.

Eже разобрался с побитовым ИЛИ, яваскрипт сравнивает числа в 32-битном представлении. Теперь проблемка с побитовым сдвигом влево.

js 30 << 30 возвращает -2147483648
php 30 << 30 возвращает 32212254720

Хорошо, первые 32 бита, 32212254720 % (2 ** 32), получим 2147483648, почти похоже на результат js.

Пытаюсь воссоздать логику js, число 30 в двоичном представлении

11110
00000000000000000000000000011110

Сдвигаю влево на 30 бит, получаю

00000000000000000000000000011110000000000000000000000000000000

Оставляю 32 бита

10000000000000000000000000000000

Конвертирую в десятичное

2147483648

Но откуда в js берется знак минус?

PS

Всем спасибо за помощь, написал 3 функции | << >>>, а потом нашел готовую библиотеку https://github.

com/simaguo/javascript-bitwise-operators

• javascript
• php
• битовые-операции

3

Из курса дискретной математики, помню:

Для записи чисел в памяти компьютера используется различная система двоичных кодов… Существует 3 вида:

1)Прямой 2)Обратный 3)Дополнительный (Коды)

Ваш компьютер использует для записи чисел — дополнительный код. Это не обычный двоичный код, в нем если первый знак является 1, то это отрицателеное число(то есть числа начинающиеся со знака 1, отрицательные числа)

Кстати Вы встретились с очень полезной ошибкой, в плане ваших знаний) Теперь знаете больше, мой совет кроме изучения языков, рассмотрите как работает ваш компьютер (это не в коем случае не наставления, просто совет))) Удачи!

1

Побитовые операторы в JavaScript работают с 32-битными целыми числами в их двоичном представлении.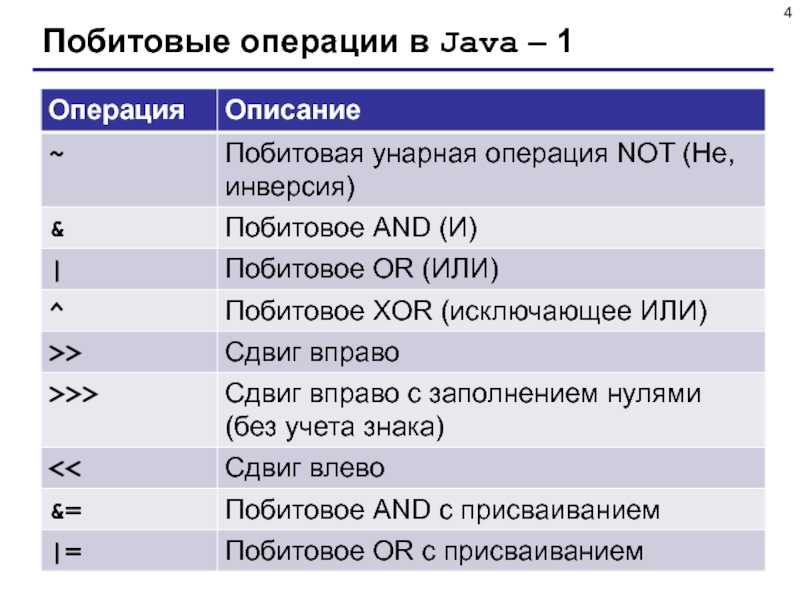

Число 30 в двоичной форме это 0b00000000000000000000000000011110 (0b — это просто префикс, говорящий о том, что данное за ним число записано в двоичной форме. Так вот, в тридцати двух битном представлении крайняя левая цифра 0 (сразу после 0b и тридцать вторая если считать справа!) — что соответствует знаку + числа идущего за префиксом).

Сдвигаем это число на 30 позиций влево 30 << 30 получаем в десятичном виде -2147483648, а двоичном (32-х битном) 0b10000000000000000000000000000000, где старшая цифра (после префикса 0b) единица, что соответствует знаку минус.

2

Ты осуществляешь операции над целыми числами со знаком. Первый бит отвечает за знак. В джаваскрипте операция js 30 << 30 возвращает 10000000000000000000000000000000 — это число в обратном коде (тебе написали выше) соответствует -2147483648 в десятичной.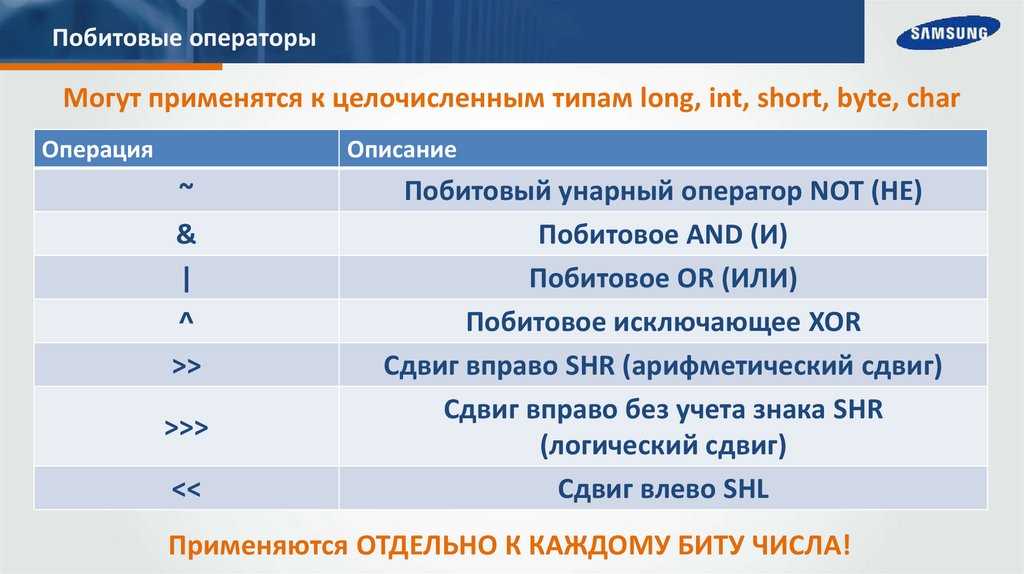 В пхп у тебя 64-битное слово, поэтому ты получается двоичное число с нулем в первом бите 000000000000000000000000000011110000000000000000000000000000000 что соответствует 32212254720 в десятичной.

Чтбы перепроверить удобно использовать программисткий калькулятор виндовс.

Если ты хочешь выполнить такую операцию на джаваскрипте — тебе нужно 64-битное целое. Используй node-int64 или goog.math.Long.html из closure-library

1

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

javascript — Точность вычислений побитовых операций

Вопрос задан 6 лет 9 месяцев назад

Изменён 6 лет 9 месяцев назад

Просмотрен 127 раз

Почему результаты разные?

PHP:

10010057100 >> 12; // 2443861

JavaScript:

10010057100 >>  12; // 346709
10010057100 >>> 12; // 346709

• javascript

5

цитата с mdn:

Битовые операции обращаются со своими операндами как с 32-х разрядными последовательностями нулей и единиц, а не как с десятичными, восьмеричными или шестнадцатиричными числами.

Таким образом все что выше — обрежется.

И немного спецификации

ShiftExpression : ShiftExpression >> AdditiveExpression

1. Let lref be the result of evaluating ShiftExpression. — lref ссылка на результат вычисления ShiftExpression
2. Let lval be GetValue(lref). — получение значения вычисления
3. ReturnIfAbrupt(lval). — проверка значения
4. Let rref be the result of evaluating AdditiveExpression. — rref ссылка на результат вычисления AdditiveExpression
5. Let rval be GetValue(rref). — получение значения вычисления
6. ReturnIfAbrupt(rval). — проверка значения
7. Let lnum be ToInt32(lval). — перевод значения левой части к Int32
8. ReturnIfAbrupt(lnum).
9. Let rnum be ToUint32(rval). — перевод значения правой части к Uint32
10. ReturnIfAbrupt(rnum).
11. Let shiftCount be the result of masking out all but the least significant 5 bits of rnum, that is,
    compute rnum & 0x1F. — shiftCount, значение на которое будет сдвинуто число, вычисляется наложением маски на rnum, отсекающей все кроме младших 5 бит
12. Return the result of performing a sign-extending right shift of lnum by shiftCount bits. The most significant bit is propagated. The result is a signed 32-bit integer. — возвращает результат знакового сдвига вправо числа lnum на shiftCount бит. Возвращаемое значение знаковое 32-х битное целое.

4

Все оказалось несколько неожиданно: Исходное число 10010057100 — 1001010100101001010101100110001100 (34 бита). PHP и в самом деле корректно посчитал: результат 1001010100101001010101 соответствует всем старшим битам.

Результат JS — 1010100101001010101 соответствует отбрасыванию трех (или двух) старших бит.

Что интересно, сложение на таких больших числах в JS работает корректно. PS. Если у кого есть PHP не под виндой — было бы интересно посмотреть на результаты сложения для 10010057100

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

побитовых операций JavaScript.

Побитовые операторы обрабатывают свои операнды… | by sonia dumitru

Побитовые операторы обрабатывают свои операнды как последовательность из 32 битов (нули и единицы), а не как десятичные, шестнадцатеричные или восьмеричные числа .

Например, десятичное число «» имеет двоичное представление 101 . Побитовые операторы выполняют свои операции над такими двоичными представлениями, но возвращают стандартные числовые значения JavaScript.

Побитовые операторы JavaScript:

Примеры:

JavaScript хранит числа как 64-битные числа с плавающей запятой, но все побитовые операции выполняются над 32-битными двоичными числами. Перед выполнением побитовой операции JavaScript преобразует числа в 32-битные целые числа со знаком. После выполнения побитовой операции результат преобразуется обратно в 64-битные числа JavaScript.

В приведенных выше примерах используются 4-битные двоичные числа без знака. Из-за этого ~ 5 возвращает 10 .

Поскольку JavaScript использует 32-битные целые числа со знаком, он не вернет 10. Он вернет -6.

00000000000000000000000000000101101 (5)

1111111111111111111111101010 (~ 5 = -6)

В целом используется самый левый бит в качестве знака минус.

Побитовое И

Когда побитовое И выполняется для пары битов, возвращается 1, если оба бита равны 1.

Один бит против 4 битов

Побитовое ИЛИ

Когда выполняется побитовое ИЛИ для пары битов, возвращается 1, если один из битов равен 1:

Один бит против 4 битов

Побитовое XOR

Когда побитовое XOR выполняется для пары битов, возвращается 1 если биты разные:

Один бит против 4 бит

JavaScript Побитовое И (&)

Побитовое И возвращает 1, только если оба бита равны 1:

Попробуйте сами:

JavaScript Побитовое ИЛИ (|)

Побитовое ИЛИ возвращает 1, если один из битов равен 1:

JavaScript Побитовое XOR (^)

Побитовое исключающее ИЛИ возвращает 1, если биты отличаются:

JavaScript Побитовое НЕ (~)

JavaScript (заполнение нулями) Побитовый сдвиг влево (

<<)

Это сдвиг влево с заполнением нулями. Один или несколько нулевых битов вставляются справа, а крайние левые биты отбрасываются:

JavaScript (сохранение знака) Побитовый сдвиг вправо (>>)

Это знак, сохраняющий сдвиг вправо. Копии крайнего левого бита вставляются слева, а крайние правые биты отбрасываются:

JavaScript (заполнение нулями) Shift Right (>>>)

Двоичные числа с одним набором битов легко понять:

Установка еще нескольких битов раскрывает двоичный шаблон:

Двоичные числа JavaScript хранятся в дополнительном коде до двух формат.

Это означает, что отрицательное число является побитовым НЕ числа плюс 1:

Источник :

W3Schools Online Web Tutorials

: голубой;} h2 {…

www.w3schools.com

MDN Web Docs

Сайт MDN Web Docs предоставляет информацию об открытых веб-технологиях, включая HTML, CSS и API для обоих веб-сайтов…

developer.mozilla.org

Bit Манипуляции в JavaScript.

Структуры данных и алгоритмы Серия 4 | Ханна Рейцель Ривера | CodeX

Манипуляции с битами — это метод изменения или работы с фактическими битами данных, представленными другим типом данных, чаще всего целым числом. Для целого числа, такого как 7, биты, которые оно представляет, записываются в двоичном виде, то есть в виде ряда слева направо из единиц и нулей, представляющих степени двойки, которые в сумме составляют целое число.

 7 = 4 + 2 + 1, что означает 
 7 = 2**2 + 2**1 + 2**0, поэтому в двоичном виде 
  7 = 111 

Возьмем другой пример, можно представить еще большие числа. как биты в двоичном формате. Нули в двоичном формате представляют степени двойки, которые не включены в сумму, читаются справа налево и начинаются с нулевой степени.

 645 = 2**9 + 2**7 + 2**2 + 2**0 
 645 = 1010000101 

Существует ограничение на то, насколько большое число может быть сохранено в виде двоично-битового кодирования. Без сомнения, переход с 32-битной на 64-битную во многих операционных системах знаком — это относится к максимальной емкости хранилища.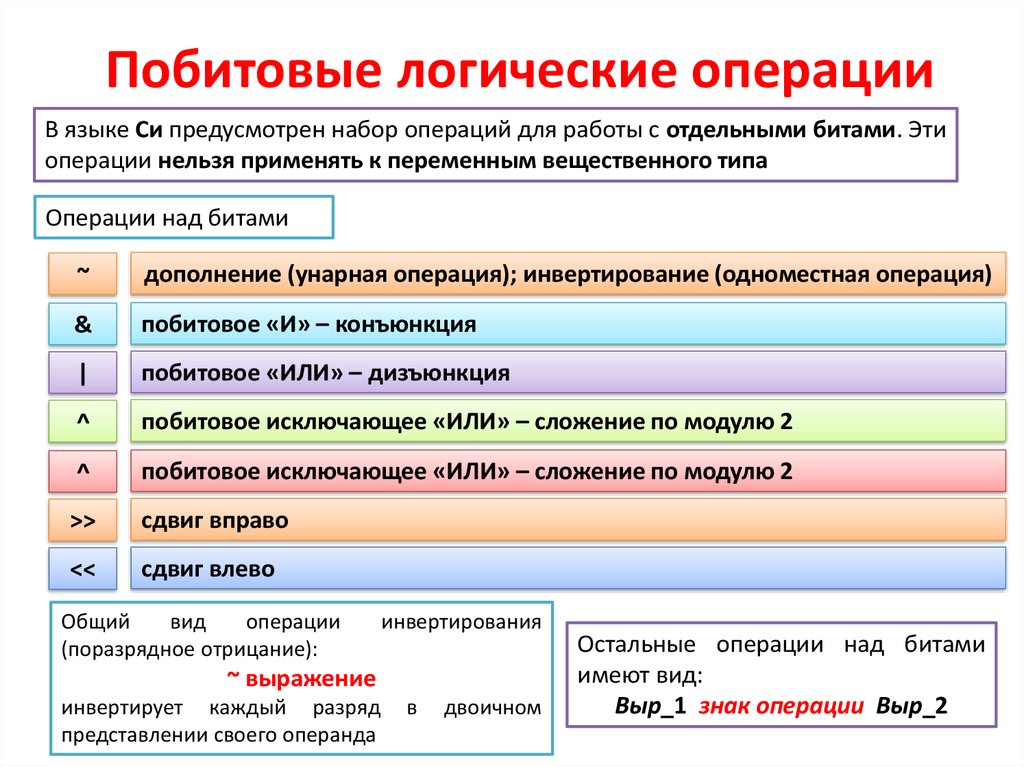 Было бы легко предположить, что наибольшее число, которое JavaScript может закодировать в двоичном виде, будет равно 64-й степени двойки (плюс 63-я степень, плюс 62-я степень…). Однако, поскольку JavaScript технически представляет все числа как числа с плавающей запятой двойной точности за кулисами, и один бит должен использоваться для представления знака, максимальное и минимальное числа, которые можно безопасно закодировать, равны 9.0007

  2**53 - 1, или MAX_SAFE_INTEGER 9 007 199 254 740 991 
 -(2**53 - 1) или MIN_SAFE_INTEGER -9 007 199 254 740 991 

Имея в виду всю эту математическую информацию, для чего мы можем использовать битовую манипуляцию? Некоторые распространенные применения помимо вопросов по кодированию на собеседовании включают сжатие и шифрование, поскольку побитовые методы с использованием алгоритмов или ключей могут использоваться для «вталкивания» данных в меньшие кадры или для преобразования битов незашифрованных данных таким образом, чтобы их можно было распознать только при наличии соответствующего шифра. .

Для выполнения битовых манипуляций у нас есть ряд готовых операторов. За некоторыми исключениями, до недавнего времени они были совершенно новыми для меня, так что обзор будет полезен всем.

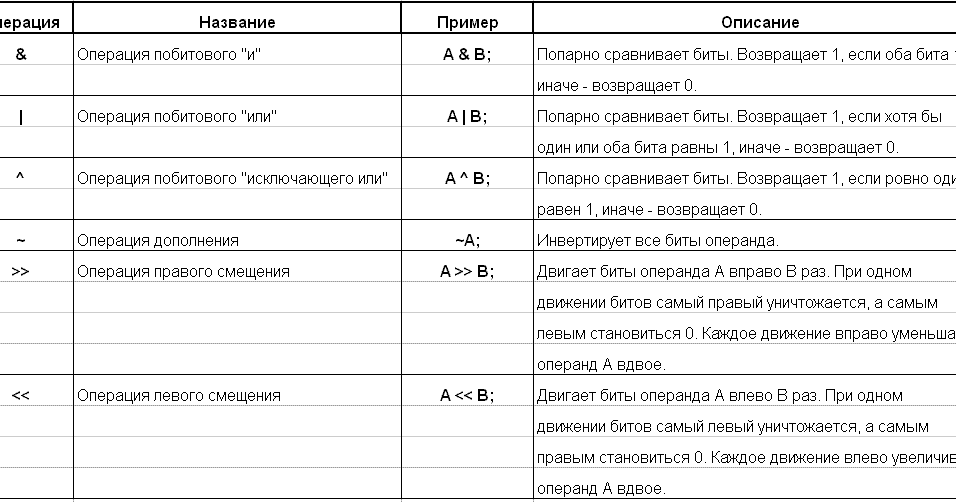
 ~ НЕ -> инвертирует каждый бит на противоположный (например, 1 -> 0) 
 & И -> сравнивает два битовых шаблона одинаковой длины; возвращает единицу в позициях, где оба шаблона имеют единицы, иначе возвращает ноль 
 | ИЛИ -> также сравнивает два битовых шаблона одинаковой длины; возвращает единицу, если какой-либо шаблон имеет единицу в этой позиции, иначе ноль 9XOR -> также сравнивает два шаблона одинаковой длины; возвращает единицу только в позициях, где шаблоны различны 
 << LEFT SHIFT -> сдвигает шаблон на определенное количество битов (указывается после оператора) и добавляет нули в конец; эквивалентно умножению начального числа на 2**n, где n — число для сдвига 
 >> ПРАВЫЙ СДВИГ -> сдвиг шаблона на определенное количество битов вправо и добавление единицы в конце; эквивалентно делению на 2**n, где n — число, которое нужно сдвинуть на 

Это не все побитовые операторы; чтобы узнать больше, ознакомьтесь с документацией здесь.

Наиболее распространенная проблема манипулирования битами, вероятно, заключается в проверке того, является ли число степенью двойки (на Leetcode есть легкодоступный вариант). Решение выглядит простым, но на самом деле его довольно сложно понять поначалу.

 const isPowerOfTwo = n => { 
 return (n && !(n & (n - 1))) 
 } 

Что это значит? Мы знаем, что возвращаем логическое значение. Первая половина возврата проверяет истинность n; то есть ненулевое. Это заботится о проверке, является ли ноль степенью двойки. Во второй части используется наш побитовый оператор И для сравнения двух битовых шаблонов одинаковой длины: n и n-1. Давайте посмотрим на эту вторую часть немного яснее на некоторых примерах.

 8 - известная степень 2 
 8 проходит первый тест; это правда, так как это не ноль 
 А как насчет 8 и 7? Давайте посмотрим на них как на двоичный код 
 8 = 1000 (2**3 + 0 + 0 + 0) 
 7 = 0111 (0 + 2**2 + 2**1 + 2**0) 
 Итак, операция 8 и 7 приводят к 0000 (ложь) 
 Следовательно, выполнение !(8 и 7) дает нам истинное значение 
 Наша функция возвращает истину! 8 это степень двойки! 

Вот как работает тест: все степени двойки будут иметь только одну единицу в своем двоичном представлении — место, в котором они являются степенью двойки. Однако вычитание единицы из степени двойки приводит к числу со многими другими экземплярами числа один, что приводит к тому, что результат побитового оператора И для обоих шаблонов всегда возвращает ложь. Поскольку мы проверяем, является ли это ложным, мы получаем логическое значение true, когда наш ввод является степенью двойки.

Другая распространенная проблема манипулирования битами — подсчет количества единиц в двоичном представлении числа. Это также известно как гиря Хэмминга, которую я нахожу бесконечно восхитительной, потому что она вызывает в воображении образы окружных ярмарок, где вместо молота и колокола силач поднимает огромную свинью с голубой лентой. Я отвлекся. Опять же, у надежного Leetcode есть готовый пример.

 const hammingWeight = n => { 
 let count = 0; 
 в то время как (n){ 
 n = n & (n - 1) 
 count++ 
 } 
 return count 
 } 

Снова кажущееся простым решение, которое на самом деле довольно сложно понять. Давайте снова разберем это на нескольких примерах.

 Найдите вес Хэмминга 103 
 Во-первых, мы видим, что наш счет равен 0 
 Затем, в то время как n -> означает всякий раз, когда n не равно нулю 
 Затем мы устанавливаем n равным n & (n - 1), а затем увеличиваем наша переменная счета 
. Для 103 двоичное представление равно 2**6 + 2**5 + 2**2 + 2**1 + 2**0, или 1100111 
 Для 102, наше начальное n - 1, двоичный код будет 1100110 
 Таким образом, в первом цикле n & (n - 1) будет 1100110, и наш счетчик повторяется для 1, который был в 2 ** 0 разряде На следующем цикл: 
 n = 1100110 (102) 
 n - 1 = 1100101 (101) 
 n = n & (n - 1) = 1100100 (100) -> счетчик теперь до 2Следующий цикл: 
 n = 1100100 (100) 
 n - 1 = 1100011 (99) 
 n = n & (n - 1) = 1100000 (96) -> счетчик теперь равен 3 Следующий цикл: 
 n = 1100000 (96) 
 n - 1 = 1011111 (95) 
 n = n & (n - 1) = 1000000 (64) -> счетчик теперь до 4 Последний цикл: 
 n = 1000000 (64) 
 n - 1 = 0111111 (63) 
 n = n & (n - 1) = 0 -> счетчик теперь до 5 Пока цикл останавливается, потому что while(n) больше недействителен 
 Счетчик возвращается (5) -> проверка на точность 
 103 было 1100111 -> 5 единиц! 

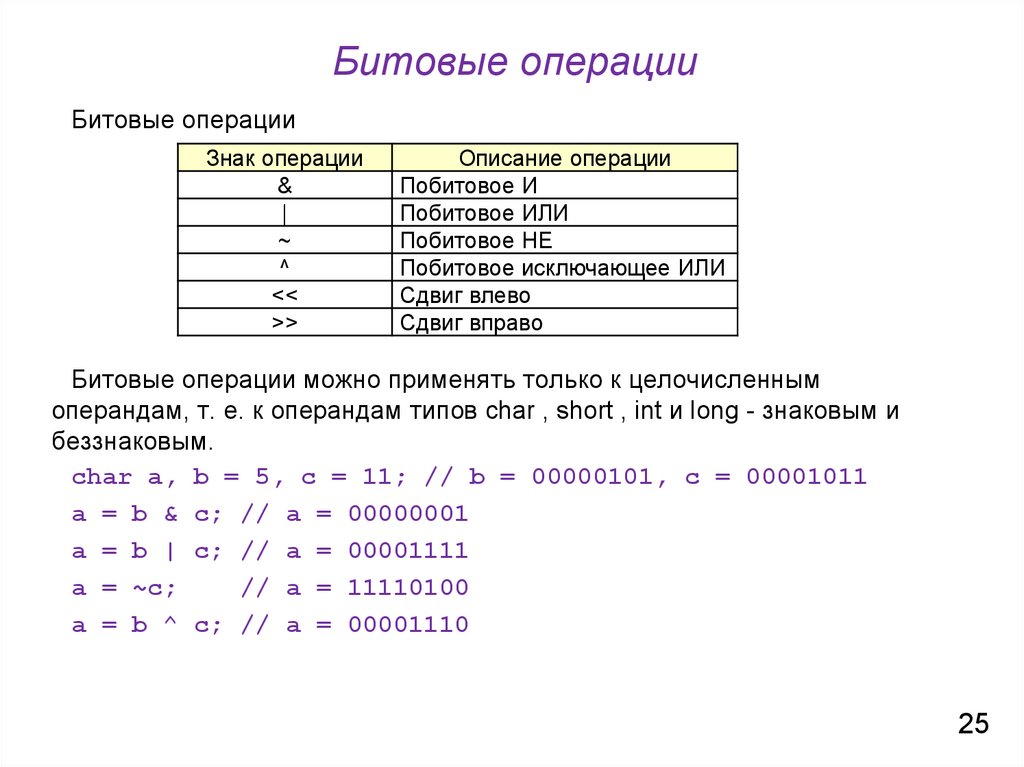
Основная идея этого метода заключается в том, что установка числа в результат побитового оператора И для предыдущего значения числа и его декремент «переворачивает» все биты справа от каждого места в числе постепенно, пока это число не станет равным нулю.