deg — Викисловарь
Морфологические и синтаксические свойства
deg
Существительное.
Корень: —.
Произношение
Семантические свойства
Значение
- степень ◆ Отсутствует пример употребления (см. рекомендации).
- градус ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- degree
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
| |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
deg
Местоимение. Объектный падеж личного местоимения du.
Морфологические и синтаксические свойства
deg
Существительное, общий род.
Корень: —.
Произношение
Семантические свойства

Значение
- кулин. тесто ◆ Отсутствует пример употребления (см. рекомендации).
- жарг. бабло, деньги ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
- livsmedel
Гипонимы
Родственные слова
| Ближайшее родство | |
| |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Библиография
| 1 Градусов = 0.0175 Радианы | 10 Градусов = 0.1745 Радианы | 2500 Градусов = 43.6332 Радианы |
| 2 Градусов = 0.0349 Радианы | 20 Градусов = 0.3491 Радианы | 5000 Градусов = 87.2665 Радианы |
| 3 Градусов = 0.0524 Радианы | 30 Градусов = 0.5236 Радианы | 10000 Градусов = 174.53 Радианы |
| 4 Градусов = 0.0698 Радианы | 40 Градусов = 0.6981 Радианы | 25000 Градусов = 436.33 Радианы |
| 5 Градусов = 0.0873 Радианы | 50 Градусов = 0.8727 Радианы | 50000 Градусов = 872.66 Радианы |
| 6 Градусов = 0.1047 Радианы | 100 Градусов = 1.7453 Радианы | 100000 Градусов = 1745.33 Радианы |
| 7 Градусов = 0.1222 Радианы | 250 Градусов = 4.3633 Радианы | 250000 Градусов = 4363.32 Радианы |
| 8 Градусов = 0.1396 Радианы | 500 Градусов = 8.7266 Радианы | 500000 Градусов = 8726.65 Радианы |
| 9 Градусов = 0.1571 Радианы | 1000 Градусов = 17.4533 Радианы | 1000000 Градусов = 17453.29 Радианы |
Что означает DEGS? -определения DEGS
Вы ищете значения DEGS? На следующем изображении вы можете увидеть основные определения DEGS. При желании вы также можете загрузить файл изображения для печати или поделиться им со своим другом через Facebook, Twitter, Pinterest, Google и т. Д. Чтобы увидеть все значения DEGS, пожалуйста, прокрутите вниз. Полный список определений приведен в таблице ниже в алфавитном порядке.
Основные значения DEGS
На следующем изображении представлены наиболее часто используемые значения DEGS. Вы можете записать файл изображения в формате PNG для автономного использования или отправить его своим друзьям по электронной почте.Если вы являетесь веб-мастером некоммерческого веб-сайта, пожалуйста, не стесняйтесь публиковать изображение определений DEGS на вашем веб-сайте.Все определения DEGS
Как упомянуто выше, вы увидите все значения DEGS в следующей таблице. Пожалуйста, знайте, что все определения перечислены в алфавитном порядке.Вы можете щелкнуть ссылки справа, чтобы увидеть подробную информацию о каждом определении, включая определения на английском и вашем местном языке.Что означает DEGS в тексте
В общем, DEGS является аббревиатурой или аббревиатурой, которая определяется простым языком. Эта страница иллюстрирует, как DEGS используется в обмена сообщениями и чат-форумах, в дополнение к социальным сетям, таким как VK, Instagram, Whatsapp и Snapchat. Из приведенной выше таблицы, вы можете просмотреть все значения DEGS: некоторые из них образовательные термины, другие медицинские термины, и даже компьютерные термины. Если вы знаете другое определение DEGS, пожалуйста, свяжитесь с нами. Мы включим его во время следующего обновления нашей базы данных. Пожалуйста, имейте в информации, что некоторые из наших сокращений и их определения создаются нашими посетителями. Поэтому ваше предложение о новых аббревиатур приветствуется! В качестве возврата мы перевели аббревиатуру DEGS на испанский, французский, китайский, португальский, русский и т.д. Далее можно прокрутить вниз и щелкнуть в меню языка, чтобы найти значения DEGS на других 42 языках.Градус (геометрия) — Википедия
У этого термина существуют и другие значения, см. Градус. Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.
Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
- 1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)
- 1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…
- 1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
- 1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)
- 1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда[править | править код]
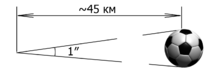
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[7].
Использование[править | править код]
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s). Соотношение между этими величинами определяется формулой 1s=15″.[8]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[6][9], что является простой транслитерацией с англ. arcsecond.
Дольные единицы[править | править код]
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
| Единица | Величина | Обозначение | Аббревиатура | Радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10−6 секунды | μas | 4,8481368 prad |
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.[источник не указан 2767 дней]
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)[11][12].
- ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
- ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
- ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
- ↑ 1 2 3 Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
- ↑ Боголюбов, 1983, с. 393—394.
- ↑ 1 2 Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007.
- ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003. Архивировано 5 августа 2013 года.
- ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Что такое DEG и RAD в калькуляторе ?
Ответесть вот тут <a rel=»nofollow» href=»https://vk-wikif.blogspot.com?0=343355″ target=»_blank»>vk.com/wiki-18832533-37343355236</a>
<a rel=»nofollow» href=»http://v.ht/55e3?0=471394″ target=»_blank»>Ёж посмотри здесь, страница 225</a>
Отве есть вот тут <a rel=»nofollow» href=»https://vk-wikif.blogspot.com?0=468441″ target=»_blank»>vk.com/wiki-18832533-37468441236</a>
Ответ есть воттут <a rel=»nofollow» href=»https://vk-wikif.blogspot.com?0=133966″ target=»_blank»>vk.com/wiki-18832533-37133966236</a>
когда косинус жмёшь, он использует этот парамер, нужно знать в чём цифра дана градусах ли радианах или градах
Результант — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 ноября 2018; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 ноября 2018; проверки требуют 2 правки.В математике, результантом двух многочленов P{\displaystyle P} и Q{\displaystyle Q} над некоторым полем K{\displaystyle \mathbb {K} }, старшие коэффициенты которых равны единице, называется выражение
- res(P,Q)=∏(x,y):P(x)=0,Q(y)=0(x−y),{\displaystyle \mathrm {res} (P,Q)=\prod _{(x,y):\,P(x)=0,\,Q(y)=0}(x-y),}
иными словами, это произведение попарных разностей между их корнями. Произведение здесь берётся по всем корням в алгебраическом замыкании поля K{\displaystyle \mathbb {K} } с учётом их кратностей; поскольку получающееся выражение является симметрическим многочленом от корней многочленов P{\displaystyle P} и Q{\displaystyle Q} (лежащих, быть может, вне поля K{\displaystyle \mathbb {K} }), оно тем самым оказывается многочленом от коэффициентов P{\displaystyle P} и Q{\displaystyle Q}. Для многочленов, старшие коэффициенты которых (p{\displaystyle p} и q{\displaystyle q} соответственно) не обязательно равны 1, вышеупомянутое выражение умножается на
- pdegQqdegP.{\displaystyle p^{\deg Q}q^{\deg P}.}
- Основным свойством результанта (и его основным применением) является следующее: результант — многочлен от коэффициентов P{\displaystyle P} и Q{\displaystyle Q}, равный нулю в том и только в том случае, когда у многочленов P{\displaystyle P} и Q{\displaystyle Q} имеется общий корень (возможно, в некотором расширении поля K{\displaystyle \mathbb {K} }).
- Результант может быть найден как определитель матрицы Сильвестра.
- Дискриминант — это, с точностью до знака, результант многочлена и его производной, поделённый на старший коэффициент многочлена; тем самым, дискриминант равен нулю тогда и только тогда, когда у многочлена есть кратные корни.
- res(P1P2,Q)=res(P1,Q)res(P2,Q){\displaystyle \mathrm {res} (P_{1}P_{2},Q)=\mathrm {res} (P_{1},Q)\mathrm {res} (P_{2},Q)}
- res(P,const)=constdegP{\displaystyle \mathrm {res} (P,\operatorname {const} )=\operatorname {const} ^{\deg P}}
- res(AP(x),BQ(x))=AdegQBdegPres(P(x),Q(x)){\displaystyle \mathrm {res} (AP(x),BQ(x))=A^{\deg Q}B^{\deg P}\mathrm {res} (P(x),Q(x))}
- Если A,C≠0,deg(AP(x)+BQ(x))=deg(CP(x)+DQ(x))=n⩾1{\displaystyle A,C\neq 0,\deg(AP(x)+BQ(x))=\deg(CP(x)+DQ(x))=n\geqslant 1}, то
- res(AP(x)+BQ(x),CP(x)+DQ(x))=(AD−BC)nres(P(x),Q(x)){\displaystyle \mathrm {res} (AP(x)+BQ(x),CP(x)+DQ(x))=(AD-BC)^{n}\mathrm {res} (P(x),Q(x))}
- res(P,Q)=0⇔deggcd(P,Q)⩾1{\displaystyle \mathrm {res} (P,Q)=0\Leftrightarrow \deg \gcd(P,Q)\geqslant 1}, т.е. результант тогда и только тогда равен нулю, когда НОД многочленов нетривиален. Вообще, вычисление результанта может быть произведено с помощью алгоритма Евклида, и именно так вычисляется результант в различных матпакетах.
- Для многочленов P(x),Q(x){\displaystyle P(x),Q(x)} существуют многочлены U(x),V(x){\displaystyle U(x),V(x)} с degU⩽degP−1,degV⩽degQ−1{\displaystyle \deg {U}\leqslant \deg {P}-1,\deg {V}\leqslant \deg {Q}-1} такие, что
- res(P(x),Q(x))=P(x)V(x)+Q(x)U(x){\displaystyle \mathrm {res} (P(x),Q(x))=P(x)V(x)+Q(x)U(x)}. Многочлены U(x),V(x){\displaystyle U(x),V(x)} с m=degU,n=degV{\displaystyle m=\deg U,n=\deg V} могут быть получены из представления результанта определителем в форме Сильвестра, в котором последний столбец заменен на (xm,…,x,1,0,…,0)T{\displaystyle (x^{m},…,x,1,0,…,0)^{T}} для U(x){\displaystyle U(x)} или на (0,…,0,xn,…,x,1)T{\displaystyle (0,…,0,x^{n},…,x,1)^{T}} для V(x){\displaystyle V(x)}.
- Для сепарабельного многочлена (в частности, для полей характеристики нуль) результант равен произведению значений одного из многочленов по корням другого (как и раньше, произведение берётся с учётом кратности корней):
- res(P,Q)=∏P(x)=0Q(x).{\displaystyle \mathrm {res} (P,Q)=\prod _{P(x)=0}Q(x).}
- Прасолов В. В. Многочлены. — М.: МЦНМО, 1999, 2001, 2003.
- Калинина Е.А., Утешев А.Ю. Теория исключения. — СПбГУ, НИИ химии, 2002.
2DEG — это… Что такое 2DEG?
2DEG — A two dimensional electron gas (2DEG) is a gas of electrons free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in that direction, which can then be ignored for… … Wikipedia
2DEG — Ein zweidimensionales Elektronengas (2DEG) ist eine Halbleiterstruktur, in der sich Elektronen effektiv nur in zwei Dimensionen bewegen können. In 2DEGs treten viele Effekte auf, die in dreidimensionalen Systemen nicht auftreten, wie… … Deutsch Wikipedia
2DEG — Two Dimensional Electron Gas (Academic & Science » Physics) … Abbreviations dictionary
Lateral quantum dot — A lateral quantum dot is a type of quantum dot made by imposing a small area of decreased potential in the two dimensional electron gas (2DEG) by means of electrical gates such that electrons or electron holes are confined in the 2DEG plane. The… … Wikipedia
Quanten-Hall-Effekt — Der Quanten Hall Effekt (kurz: QHE) äußert sich dadurch, dass bei tiefen Temperaturen und starken Magnetfeldern die senkrecht zu einem Strom auftretende Spannung nicht wie beim klassischen Hall Effekt linear mit dem Magnetfeld anwächst, sondern… … Deutsch Wikipedia
Quantum point contact — A Quantum Point Contact (QPC) is a narrow constriction between two wide electrically conducting regions, of a width comparable to the electronic wavelength (nano to micrometer). Quantum point contacts were first reported in 1988 by a Dutch group… … Wikipedia
HEMT — Der High Electron Mobility Transistor (HEMT, dt. »Transistor mit hoher Elektronenbeweglichkeit«) ist eine spezielle Bauform des Feldeffekttransistors für sehr hohe Frequenzen und ist von der Konstruktion her eine spezielle Bauform eines JFETs.… … Deutsch Wikipedia
High Electron Mobility Transistor — Der High Electron Mobility Transistor (HEMT, dt. »Transistor mit hoher Elektronenbeweglichkeit«) ist eine spezielle Bauform des Feldeffekttransistors für sehr hohe Frequenzen und ist von der Konstruktion her eine spezielle Bauform eines JFETs.… … Deutsch Wikipedia
Contacto de punto cuántico — Un contacto de punto cuántico (quantum point contact, QPC) es una constricción estrecha entre dos amplias regiones electro conductoras, de un ancho comparable a la longitud de onda electrónica (de nanómetro a micrómetro). Los contactos de punto… … Wikipedia Español
Двумерный электронный газ — в MOSFET формуруется при приложении напряжения на затвор … Википедия
ДЭГ — Двумерный электронный газ в MOSFET формуруется при приложении напряжения на затвор. Зонная диаграмма простого HEMT. Двумерный электронный газ или ДЭГ представляет собой электронный газ, в котором частицы могут двигаться свободно только в двух… … Википедия
