Циклы в с – Циклы в Си. Циклы с постусловием, предусловием, Цикл for со счётчиком.

Циклы в языке программирования С (Си) для микроконтроллеров AVR

В данной статье будут рассмотрены циклы в языке программирования Си для микроконтроллеров AVR. Будут рассмотрены циклы типа «для» (for) и циклы типа «пока» (while), будет показано как осуществить принудительное прерывание цикла и организовать бесконечный цикл. Рассмотрены вопросы вложенных циклов и формирования длительных временных задержек.

Для того чтобы несколько раз повторить какую-либо последовательность действий, применяют алгоритмические конструкции, называемые циклами. Саму последовательность действий при этом называют телом цикла.

В языке С есть две разновидности циклов: циклы со счетчиком (типа «для» или for) и цикл с условием (типа «пока» или while). В других языках программирования, например Pascal, циклы с условием разделялись на циклы с предусловием (типа while) и циклы с пост условием (типа repeat until), но в современных языках программирования циклы с пост условием постепенно отмирают.

Циклы типа «для» (for)

Циклы типа «для» (for) применяются в ситуациях, в которых заранее известно количество повторений цикла. Поэтому в составе подобного цикла всегда есть так называемый «счетчик повторений» или «переменная цикла». Пример использования цикла for в языке представлен на следующем рисунке.

В данном примере тело цикла повторится столько раз, сколько значений «пробежит» переменная цикла i от своего начального значения, задаваемого операцией присваивания i = a, до конечного значения, задаваемого условием i < b. Изменение переменной i определяется условием присваивания вида i = i + c. Но чаще всего в циклах типа for в языке С переменная цикла изменяется за одно повторение цикла на +1 или -1, поэтому используется запись вида i++ (инкремент переменной цикла) или i— (декремент переменной цикла). В рассмотренном примере при i = b цикл завершается и выполняется оператор, следующий за закрывающей скобкой цикла.

Рассмотрим пример цикла for, приведенный на следующем рисунке.

В этом примере на первом шаге цикла переменная i будет равна 1, перед вторым шагом произойдет ее увеличение на 1 в результате инкремента (i++) и она станет равной 2. На третьем шаге значение переменной цикла i будет равно 3. И так до тех пор, пока на пятом шаге цикла она не станет равной 5. В результате следующей операции инкрементирования (i++) переменная цикла получит значение 6, но условие i <= 5 уже не будет истинным, поэтому цикл завершится. Таким образом, тело цикла будет выполнено 5 раз.

Язык С допускает инициализацию переменной цикла в его оглавлении как показано на следующем рисунке.

Но начинающим лучше производить инициализацию переменной цикла в начале функции вместе с остальными инициализируемыми переменными – более подробно читайте об этом в статье про переменные в языке С.

Усовершенствуем программу управления миганием светодиода, рассмотренную в статье про программирование портов микроконтроллеров AVR, с помощью цикла типа «для» (for). Заставим светодиод мигать 10 раз.

Пример подобной программы представлен на следующем рисунке.

Циклы типа «пока» (while)

Цикл типа while («пока») повторяется до тех пор, пока истинно условие цикла. Поэтому часто его называют циклом с условием. В простейшем виде запись данного цикла выглядит следующим образом:

while (условие)
{
// тело_цикла
}

Циклы с условием необходимы в тех случаях, когда заранее не известно число повторений цикла. Подобный цикл будет работать до тех пор, пока выполняется условие.

Чтобы цикл завершился, внутри него (в его теле) должно происходить изменение какой-либо переменной, которая входит в условие цикла.

Пример:

int y;

y = 50;

while (y > 0)
{
y = y — 1;
}

В этом примере тело цикла будет повторено (выполнится) 50 раз, до тех пор пока переменная y будет больше нуля. На каждом шаге цикла значение переменной y будет уменьшаться на 1. И когда оно станет равным 0, цикл завершится.

Оператор break

С помощью данного оператора можно в любой момент завершить цикл (прервать его выполнение). Обычно это делается при наступлении каких-нибудь особых условий.

В большинстве случаев он используется следующим образом:

if (условие1) break;

Данную последовательность операторов можно записать в любом месте цикла. Но опытные программисты стараются все таки избегать использования данного оператора – для улучшения читаемости и отладки программы желательно в условии цикла прописывать все ситуации, при которых будет нужен выход из цикла.

Бесконечные циклы

Бесконечный цикл в языке программирования С можно осуществить как с помощью цикла «для» (for), так и с помощью цикла «пока» (while). Синтаксис подобных циклов выглядит следующим образом.

for(;;)
{
// тело_цикла
}

или

while (1)
{
// тело_цикла
}

Чаще применяется способ с циклом типа while – он более нагляден. Выйти из подобных циклов можно единственным образом – применив рассмотренный в предыдущем разделе оператор break.

Бесконечные циклы находят широкое распространение в программах для микроконтроллеров, потому что данные программы должны, как правило, работать постоянно до тех пор, пока устройство не обесточат. Много примеров подобных программ вы можете найти на нашем сайте в рубрике «схемы и устройства на микроконтроллерах AVR«.

Вложенные циклы

В большинстве известных в настоящее время языках программирования (и язык Си этому не исключение) допускается использование вложенных циклов – то есть когда один цикл выполняется в теле другого. Пример использования такой конструкции приведен на следующем рисунке:

Рассмотрим пример двух вложенных друг в друга циклов «для». Тело вложенного цикла в общей сложности будет повторено 200 раз.

В этом примере тело вложенного цикла будет выполнено 200 раз.

Формирование задержки

Аппаратные средства микроконтроллеров AVR не могут формировать длительные задержки – но это, собственно говоря, не очень и нужно потому что сколь угодно длительную задержку можно организовать с помощью циклов (лишь бы имелась возможность формирования хотя бы небольшой задержки). Пример организации задержки длительностью 10 минут с помощью цикла и функции _delay_ms() представлен на следующем рисунке:

Менструальный цикл — Википедия

Изменения уровней гормонов и гистологических особенностей эндометрия матки в ходе менструального цикла

Менструа́льный цикл (от лат. menstruus «месячный «цикл»; ежемесячный») — это регулярное естественное изменение, которое происходит в женской репродуктивной системе (особенно в матке и яичниках), что делает беременность возможной

[1]^[2]. Цикл необходим для производства ооцитов и для подготовки матки к беременности^[1]. Менструальный цикл происходит из-за подъема или падения гормонов^[3]. Этот цикл приводит к утолщению слизистой оболочки матки и росту яйцеклетки (что необходимо для беременности)^[3]. Яйцо выпускается из яичника около четырнадцатого дня в цикле; утолщенная слизистая оболочка матки обеспечивает питательные вещества для эмбриона после имплантации^[3]. Если беременность не наступает, подкладка выпущена, что известно как менструация^[3].

До 80% женщин сообщают о наличии некоторых симптомов в течение одной-двух недель до менструации^[4]. Общие симптомы включают прыщи, вздутие живота, чувство усталости, раздражительность и изменения настроения^[5]. Эти симптомы мешают нормальной жизни и поэтому квалифицируются как предменструальный синдром у 20-30% женщин. У 3-8% они тяжелые

[4].

Первый период обычно начинается в возрасте от двенадцати до пятнадцати лет, момент, известный как менархе^[6]. Он может иногда начинаться уже в восемь, и такое начало все еще может быть нормальным^[3]. Средний возраст первого периода, как правило, позже в развивающихся странах и раньше в развитых странах. Типичная продолжительность времени между первым днем одного периода и первым днем следующего составляет от 21 до 45 дней у молодых женщин и от 21 до 35 дней у взрослых (в среднем 28 дней)^[3][7]. Менструация прекращается после менопаузы, которая обычно происходит в возрасте от 45 до 55 лет^[8]. Кровотечение обычно длится от 3 до 7 дней^[3].

Менструальный цикл зависит от гормональных изменений^[3]. Эти изменения меняют с помощью гормональной контрацепции, чтобы предотвратить беременность

[9]. Каждый цикл можно разделить на три фазы в зависимости от событий в яичнике (цикл яичников) или в матке (цикл матки)^[1]. Яичниковый цикл состоит из фолликулярной фазы, овуляции и лютеиновой фазы, тогда как маточный цикл делится на менструацию, пролиферативную фазу и секреторную фазу.

Менструальный цикл характерен для человека, некоторых других приматов^[10], китов.

Менструальный цикл включает три фазы: менструальную, пролиферативную и секреторную

.^[11].

Длительность менструального цикла женщины (в среднем) 28^[12]±7 суток.

Продолжительность цикла определяется физиологическими процессами в организме женщины.

Менархе — первый менструальный цикл — является центральным событием в период полового развития, указывающим на способность женского организма к размножению. У женщин средним возрастом наступления менархе считаются 12-14 лет, с нормой от 9 до 15 лет: 9 лет — ранняя менархе, после 15 лет — первичная аменорея. Время наступления первого менструального кровотечения зависит от таких факторов, как наследственность, питание, общее состояние здоровья.

Нарушения периода менструального цикла могут быть вызваны различными факторами: от подростковых гормональных колебаний, беременности и других естественных причин до различных внешних и внутренних стрессов.

Прекращение менструаций происходит в возрасте 40—58 лет (в среднем, в 47—50 лет), в период климакса происходит угасание репродуктивной функции. Время наступления менопаузы (климакс — период, характеризующийся нерегулярностью или полным прекращением менструаций) зависит в большей степени от наследственности, однако некоторые заболевания и врачебные вмешательства могут вызвать раннее наступление менопаузы.

Процессы в яичнике в течение менструального цикла:
1 Менструация
2 Созревающий фолликул
3 Граафов фолликул
4 Овуляция
5 Жёлтое тело
6 Жёлтое тело прекращает функционировать

Процессы, происходящие в течение менструального цикла, могут быть описаны как фазы, соответствующие изменениям в яичниках (фолликулярная, овуляторная и лютеиновая), и в эндометрии (менструальная, пролиферативная и секреторные фазы).

Фолликулярная/менструальная фаза[править | править код]

Менструальная фаза представляет собой кровотечение из полости матки в результате отторжения слоя эндометрия, которое происходит в конце овариального цикла, если не было оплодотворения яйцеклетки. Началом фолликулярной фазы яичника или менструальной фазы матки считается первый день менструации. Длительность фолликулярной фазы, во время которой происходит окончательное созревание доминантного фолликула, индивидуальна для каждой женщины: от 7 до 22 дней, в среднем 14 дней.

Фолликулярная фаза (а вместе с ней и овариальный цикл) начинается с выделения гонадолиберина гипоталамусом, который стимулирует аденогипофиз к секреции небольших количеств фолликулостимулирующего и лютеинизирующего гормонов (фоллитропина и лютропина соответственно). Низкий уровень секреции эстрадиола подавляет секрецию фоллитропина и лютропина, оставляя уровень их секреции относительно невысоким. Тем не менее, под действием фоллитропина в яичниках начинают развиваться несколько фолликулов, из которых становится доминантным фолликул, имеющий наибольшее число рецепторов к фолликулотропину и наиболее интенсивно синтезирующий эстрадиол, остальные же подвергаются атрезии. Постепенно уровень эстрадиола растёт, но, хотя низкая концентрация эстрадиола подавляет секрецию гонадотропинов, высокая концентрация эстрадиола, напротив, стимулирует секрецию гонадотропинов, так как она приводит к увеличению выделения гонадолиберина гипоталамусом. Особенно этот эффект заметен для лютропина, поскольку высокая концентрация эстрадиола увеличивает чувствительность к гонадолиберину клеток аденогипофиза, выделяющих лютропин. Кроме того, фолликулы сильнее реагируют на лютропин из-за большего числа рецепторов к этому гормону. Таким образом, в этом случае имеет место регуляция по принципу положительной обратной связи. Итак, фолликул увеличивается в размерах до тех пор, пока не произойдёт резкий выброс лютропина из аденогипофиза. На этом фолликулярная фаза заканчивается и начинается овуляторная фаза^[13][14].

Овуляторная/пролиферативная фаза[править | править код]

Приблизительно к седьмому дню цикла определяется доминантный фолликул, который продолжает расти и секретирует увеличивающееся количество эстрадиола, в то время как остальные фолликулы подвергаются обратному развитию. Достигнувший зрелости и способный к овуляции фолликул называется граафовым пузырьком. Во время овуляторной фазы, которая длится около трёх дней, происходит выброс лютеинизирующего гормона (ЛГ). В течение 36—48 ч происходит несколько волн высвобождения ЛГ, значительно увеличивается его концентрация в плазме. Выброс ЛГ завершает развитие фолликула, стимулирует продукцию простагландинов и протеолитических ферментов, необходимых для разрыва стенки фолликула и высвобождения зрелой яйцеклетки (собственно овуляция). В то же время снижается уровень эстрадиола, что иногда сопровождается овуляторным синдромом. Овуляция обычно происходит в ближайшие 24 ч после наиболее крупной волны выброса ЛГ (от 16 до 48 ч). Во время овуляции высвобождается 5—10 мл фолликулярной жидкости, в которой содержится яйцеклетка^[13][14].

Лютеиновая/секреторная фаза[править | править код]

Промежуток времени между овуляцией и началом менструального кровотечения называется лютеиновой фазой цикла (также известна как фаза жёлтого тела). В отличие от фолликулярной фазы, длительность лютеиновой более постоянная — 13—14 дней (± 2 дня). После разрыва граафова пузырька стенки его спадаются, его клетки накапливают липиды и лютеиновый пигмент, это придаёт ему жёлтый цвет. Трансформированный граафов фолликул теперь называется жёлтым телом. Продолжительность лютеиновой фазы зависит от периода функционирования (10—12 дней) жёлтого тела, в это время жёлтое тело секретирует прогестерон, эстрадиол и андрогены. Повышенный уровень эстрогена и прогестерона изменяет характеристику двух наружных слоев эндометрия. Железы эндометрия созревают, пролиферируют и начинают секретировать (секреторная фаза), матка готовится к имплантации оплодотворенной яйцеклетки. Уровень прогестерона и эстрогена достигают пика в середине лютеиновой фазы, и в ответ на это снижается уровень ЛГ и ФСГ.

При наступлении беременности жёлтое тело начинает вырабатывать прогестерон до тех пор, пока плацента не разовьётся и не станет секретировать эстроген и прогестерон.

Если беременность не происходит, жёлтое тело прекращает функционировать, снижается уровень эстрогенов и прогестерона, что приводит к отечности и некротическим изменениям эндометрия. Снижение уровня прогестерона также усиливает синтез простагландинов. Если яйцеклетка не оплодотворяется, то через некоторое время жёлтое тело подвергается лютеолизу^[en], то есть лизису или структурному разрушению, и более неспособно синтезировать прогестерон и эстрадиол. Регулятором лютеолиза является простагландин PGF₂^—[en]. Из-за лютеолиза секреция фоллитропина и лютропина более не подавляется, поскольку более нет отрицательной обратной связи, и секреция этих гормонов начинает возрастать, стимулируя развитие нового фолликула. Уменьшение уровня эстрогена и прогестерона также способствует возобновлению синтеза ЛГ и ФСГ, начинается новый менструальный цикл^[13][14].

1. ↑ ^{1 2 3} Silverthorn, Dee Unglaub. Human Physiology: An Integrated Approach (неопр.). — 6th. — Glenview, IL: Pearson Education (англ.)русск., 2013. — С. 850—890. — ISBN 978-0-321-75007-5.
2. ↑ Sherwood, Laurelee. Human Physiology: From Cells to Systems (неопр.). — 8th. — Belmont, California: Cengage (англ.)русск., 2013. — С. 735—794. — ISBN 978-1-111-57743-8.
3. ↑ ^{1 2 3 4 5 6 7 8} Menstruation and the menstrual cycle fact sheet (неопр.). Office of Women’s Health, USA (23 декабря 2014). Дата обращения 25 июня 2015. Архивировано 26 июня 2015 года.
4. ↑ ^{1 2} Biggs, WS; Demuth, R. H. Premenstrual syndrome and premenstrual dysphoric disorder (англ.) // American Family Physician (англ.)русск. : journal. — 2011. — 15 October (vol. 84, no. 8). — P. 918—924. — PMID 22010771.
5. ↑ Premenstrual syndrome (PMS) fact sheet (неопр.). Office on Women’s Health, USA (23 декабря 2014). Дата обращения 23 июня 2015. Архивировано 28 июня 2015 года.
6. ↑ Women’s Gynecologic Health (неопр.). — Jones & Bartlett Publishers (англ.)русск., 2011. — С. 94. — ISBN 9780763756376.
7. ↑ American Academy of Pediatrics Committee on, Adolescence; American College of Obstetricians and Gynecologists Committee on Adolescent Health, Care; Diaz, A; Laufer, MR; Breech, L. L. Menstruation in girls and adolescents: using the menstrual cycle as a vital sign (англ.) // Pediatrics (англ.)русск. : journal. — American Academy of Pediatrics (англ.)русск., 2006. — November (vol. 118, no. 5). — P. 2245—2250. — DOI:10.1542/peds.2006-2481. — PMID 17079600.
8. ↑ Menopause: Overview (неопр.). NIH (28 июня 2013).
9. ↑ Klump K. L., Keel P. K., Racine S. E., Burt S. A., Burt A. S., Neale M., Sisk C. L., Boker S., Hu J. Y. The interactive effects of estrogen and progesterone on changes in emotional eating across the menstrual cycle (англ.) // J Abnorm Psychol (англ.)русск. : journal. — 2013. — February (vol. 122, no. 1). — P. 131—137. — DOI:10.1037/a0029524. — PMID 22889242.
10. ↑ Campbell, 2011, p. 1010.
11. ↑ Ткаченко, 2009, с. 469—470.
12. ↑ Losos, Jonathan B.; Raven, Peter H.; Johnson, George B.; Singer, Susan R. (2002lkmnlnl). Biology. New York: McGraw-Hill. pp. 1207-09. ISBN 0-07-303120-8.
13. ↑ ^{1 2 3} Ткаченко, 2009, с. 466—469.
14. ↑ ^{1 2 3} Campbell, 2011, p. 1008—1009.

• Ткаченко Б. И., Брин В. Б., Захаров Ю. М., Недоспасов В. О., Пятин В. Ф. . Физиология человека. Compendium / Под ред. Б. И. Ткаченко. — М.: ГЭОТАР-Медиа, 2009. — 496 с. — ISBN 978-5-9704-0964-0.
• Campbell N. A., Reece J. B., Urry L. A. e. a. . Biology. 9th ed. — Benjamin Cummings, 2011. — 1263 p. — ISBN 978-0-321-55823-7.

Циклические соединения — Википедия

Материал из Википедии — свободной энциклопедии

Циклические соединения — химические соединения, в которых присутствует три или более связанных атомов, образующие кольцо^[1]. Соединение, кольцо которого включает 9 и более атомов, называется макроциклическим.

По атомарному составу:

По количеству циклов:

По наличию ароматическое кольца:

Отдельно выделяют соединения с топологической связью: катенаны и ротаксаны, — а также циклофаны.

• 

  Пирролидин, алициклическое гетероциклическое соединение.

• 

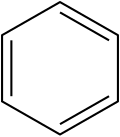
  Бензол, ароматическое карбоциклическое соединение.

• 

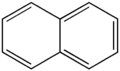
  Нафталин, полициклическое карбоциклическое соединение.

• 

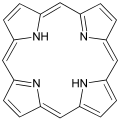
  Порфин, макроциклическое карбоциклическое соединение.

• 

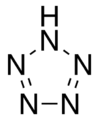
  Пентазол, неорганическое циклическое соединение.

Реакции циклизации и раскрытия цикла[править | править код]

Конденсация Дикмана

Органическая реакция, приводящая к формированию циклической структуры в одном или нескольких продуктах называется циклизацией, реакция же с разрывом кольца называется раскрытием цикла.

Разновидность циклизации, при которой к существующей циклической системе достраивается карбо- или гетероцикл, называется аннелированием.

Примеры реакций циклизации:

Примеры реакций с раскрытием цикла:

Цикл (теория графов) — Википедия

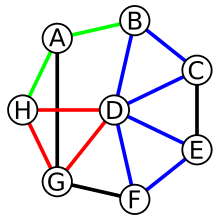Граф с окрашенными рёбрами для иллюстрации пути H-A-B, замкнутого пути или обхода с повторением вершин B-D-E-F-D-C-B и цикла без повторения рёбер или вершин H-D-G-H

В теории графов два типа объектов обычно называются циклами.

Один тип циклов, чаще называющиеся замкнутым обходом, состоит из последовательности вершин, начинающейся и заканчивающейся в той же самой вершине, и каждые две последовательные вершины в последовательности смежны. Другой тип циклов, иногда называемых простыми циклами, — это замкнутые обходы без повторного прохода по ребру или посещения вершины дважды, за исключением начальной и конечной вершин. Простые циклы можно описать набором рёбер, в отличие от замкнутых обходов, в которых наборы рёбер (с возможным повторением) не определяют однозначно порядок вершин. Ориентированный цикл в орграфе — это последовательность вершин, начинающаяся и завершающаяся в той же самой вершине, и в этой последовательности для любых двух последовательных вершин существует дуга из более ранней в более позднюю. Такое же различие между простыми циклами и обходами, как выше, можно определить и для ориентированных графов^[1].

Цикл без хорд в графе, также называемый дырой или порождённым циклом, — это цикл, в котором никакие две вершины цикла не соединены ребром, разве что это ребро само принадлежит циклу. Антидыра — это дополнение дыры. Графы без хорд можно использовать для описания совершенных графов — согласно строгой теореме о совершенных графах^[en] граф является совершенным в том и только в том случае, когда он не содержит дыр и антидыр с нечётным числом вершин больше трёх. Хордальный граф — это специальный тип совершенных графов, в котором нет дыр размером больше трёх.

Обхват графа — это длина наименьшего цикла. Этот цикл обязательно не будет иметь хорд. Клетки — это наименьшие регулярные графы с заданной степенью вершин и обхватом.

Периферийный цикл — это цикл в графе со свойством, что любые два ребра, не принадлежащие циклу, можно соединить путём внутренние точки которого не принадлежат циклу. В графе, не образованном добавлением одного ребра к циклу, периферийный цикл должен быть порождённым циклом.

Понятие цикл может также относиться к элементам пространства циклов^[en] графа. Оно состоит из множеств рёбер, которые имеют чётную степень для каждой вершины. Множества образуют векторное пространство над конечным полем из двух элементов. Используя методы алгебраической топологии его можно обобщить до векторных пространств или модулей над другими кольцами, такими как целые числа, вещественные числа и т. д. По теореме Веблена любой элемент пространства циклов можно получить путём комбинирования простых циклов. База циклов графа — это множество простых циклов, которые образуют базис пространства циклов^[2][3].

Неориентированный граф имеет цикл в том и только в том случае, когда поиск в глубину (DFS) находит ребро, которое приводит к уже посещённой вершине (обратная дуга)^[4]. Таким же образом, все обратные рёбра, которые алгоритм DFS обнаруживает, являются частями циклов^[5]. Для неориентированных графов требуется только время O(n) для нахождения цикла в графе с n вершинами, поскольку максимум n − 1 рёбер могут быть рёбрами дерева.

Ориентированный граф имеет цикл в том и только в том случае, когда DFS находит обратную дугу. Дуги вперёд и поперечные дуги не обязательно говорят о цикле. Многие алгоритмы топологических сортировок также обнаруживают циклы, поскольку они мешают существованию топологического порядка. Если ориентированный граф разделён на компоненты сильной связности, циклы существуют только в компонентах, но не между ними, поскольку циклы сильно связаны^[5].

Приложения алгоритмов нахождения циклов включают графы ожидания для нахождения взаимных блокировок в системах с параллельными потоками^[6].

В работе 1736 года о проблеме семи мостов Кёнигсберга, общепринято считающейся днём рождения теории графов, Леонард Эйлер доказал, что для того, чтобы конечный неориентированный граф имел замкнутый обход всех рёбер ровно по одному разу, необходимо и достаточно, чтобы он был связан и имел чётную степень всех вершин. Соответствующее описание существования замкнутого обхода каждого ребра ровно один раз в ориентированном графе состоит в требовании, чтобы граф был сильно связан и каждая вершина имела одинаковое число входящих и исходящих дуг. В обоих случаях полученный путь известен как эйлеров цикл. Если конечный неориентированный граф имеет чётную степень каждой вершины, независимо от того, связан он или нет, можно найти множество простых циклов, которые покрывают каждое ребро ровно раз — это Теореме Веблена^[7]. Если связный граф не удовлетворяет условиям теоремы Эйлера, замкнутый обход минимальной длины, покрывающий все рёбра по меньшей мере один раз может быть найден, тем не менее, за полиномиальное время путём решения задачи об инспекции дорог^[en].

Задача поиска простого цикла, проходящего через каждую вершину ровно один раз, в отличие от покрытия рёбер, намного сложнее. Такие циклы известны как гамильтоновы циклы, и задача определения существуют ли такие циклы NP-полна^[8]. Опубликовано множество исследований относительно классов графов, заведомо содержащих гамильтоновы циклы. Примером может служить теорема Оре о том, что гамильтонов цикл может быть найден в графе всегда, если при сложении степеней любой пары несмежных вершин получим по меньшей мере общее число вершин графа^[9].

Гипотеза о двойном покрытии циклами утверждает, что для любого графа без мостов существует мультимножество простых циклов, покрывающих каждое ребро графа в точности два раза. Доказательство гипотезы, либо контрпример пока не найдены^[10].

Некоторые важные классы графов можно определить или описать их циклами. Это:

1. ↑ V. K. Balakrishnan. Schaum’s outline of theory and problems of graph theory. — McGraw-Hill, 2005. — ISBN 978-0070054899.
2. ↑ Jonathan L. Gross, Jay Yellen. 4.6 Graphs and Vector Spaces // Graph Theory and Its Applications. — 2nd. — CRC Press, 2005. — С. 197—207. — ISBN 9781584885054.
3. ↑ Reinhard Diestel. 1.9 Some linear algebra // Graph Theory. — Springer, 2012. — Т. 173. — С. 23—28. — (Graduate Texts in Mathematics).. Перевод: Рейнгард Дистель. 1.9 Немного линейной алгебры // Теория графов. — Новосибирск: Издательство Института математики, 2002. — С. 35—40. — ISBN 5-86134-101-X..
4. ↑ Alan Tucker. Chapter 2: Covering Circuits and Graph Colorings // Applied Combinatorics. — 5th. — Hoboken: John Wiley & sons, 2006. — С. 49. — ISBN 978-0-471-73507-6.
5. ↑ ^{1 2} Robert Sedgewick. Graph algorithms. — Addison-Wesley, 1983. — ISBN 0-201-06672-6.
6. ↑ Abraham Silberschatz, Peter Galvin, Greg Gagne. Operating System Concepts. — John Wiley & Sons, INC., 2003. — С. 260. — ISBN 0-471-25060-0.
7. ↑ Oswald Veblen. An Application of Modular Equations in Analysis Situs // Annals of Mathematics. — 1912. — Т. 14, вып. 1. — С. 86—94.
8. ↑ Richard M. Karp. Complexity of Computer Computations / R. E. Miller and J. W. Thatcher. — New York: Plenum, 1972. — С. 85—103.
9. ↑ Ø. Ore. Note on Hamilton circuits // American Mathematical Monthly. — 1960. — Т. 67, вып. 1. — С. 55.
10. ↑ F. Jaeger. Annals of Discrete Mathematics 27 — Cycles in Graphs. — 1985. — Т. 27. — С. 1—12. — (North-Holland Mathematics Studies). — DOI:10.1016/S0304-0208(08)72993-1.

Циклы Китчина — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 марта 2013; проверки требуют 17 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 марта 2013; проверки требуют 17 правок.

Циклы Китчина — краткосрочные экономические циклы с характерным периодом 2-4 года, открытые в 1920-е годы английским экономистом Джозефом Китчином^[1]. Сам Джозеф объяснял существование краткосрочных циклов колебаниями мировых запасов золота^[2], однако в наше время такое объяснение не может считаться удовлетворительным. В современной экономической теории механизм генерирования этих циклов обычно связывают с запаздываниями по времени (временными лагами) в движении информации, влияющими на принятие решений коммерческими фирмами.

На улучшение конъюнктуры фирмы реагируют полной загрузкой мощностей, рынок наводняется товарами, через какое-то время на складах образуются чрезмерные запасы товаров, после чего принимается решение о снижении загрузки мощностей, но с определенным запаздыванием, так как информация о превышении предложения над спросом сама обычно поступает с определенным запаздыванием, кроме того требуется время на то, чтобы эту информацию проверить; определенное время требуется и на то, чтобы принять и утвердить само решение. Кроме того наблюдается определенное запаздывание между принятием решения и актуальным уменьшением загрузки мощностей (на проведение решения в жизнь тоже требуется время). Наконец, ещё один временной лаг существует между моментом начала снижения уровня загрузки производственных мощностей и актуальным рассасыванием избыточных запасов товаров на складах. В отличие от циклов Китчина в рамках циклов Жюгляра мы наблюдаем колебания не просто в уровне загрузки существующих производственных мощностей (и, соответственно, в объеме товарных запасов), но и колебания в объемах инвестиций в основной капитал^[3].

Например, объемы добычи нефти на сланцевых формациях в США существенно зависят от динамики цены нефти марки WTI. Примерно через полгода после изменения цены меняется буровая активность (инвестиции в основной капитал), а вместе с ней и объемы добычи. Эти изменения и их ожидания столь значительны, что сами влияют на цену нефти и значит на объемы добычи в будущем.

Эти закономерности на математическом языке описываются дифференциальным уравнением добычи со смещенным аргументом^[4].

Типичным примером цикла Китчина является краткосрочный экономический подъём между не менее краткосрочными спадами Финансово-экономическим кризисом в России (2008—2010) и Валютным кризисом в России (2014—2015) в совокупности укладывающиеся в периодичность циклов Жюгляра и являющиеся его подфазой. Определяющиеся как мало значительные, на фоне циклов Кузнеца и совсем не значительные на фоне циклов Кондратьева.

цикл — Викисловарь

Морфологические и синтаксические свойства[править]

цикл

Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -цикл- ^{[Тихонов, 1996]}.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. повторяющаяся во времени последовательность событий, процессов или явлений ◆ Я узнал, что кольца деревьев указывают на какую-то пульсацию климата, на какие-то циклы жизнедеятельности планеты, не совпадающие ни с периодом солнечной активности, ни с чем иным. Ю. О. Домбровский, «Хранитель древностей» (цитата из Национального корпуса русского языка, см. Список литературы)
2. совокупность взаимосвязанных дисциплин, работ или произведений, образующих законченную стройную систему ◆ В поэтическом цикле автор обычно знает или чувствует, какое именно стихотворение задаёт тональность всему циклу. Вадим Крейд, «Георгий Иванов в Йере», 2003 г. (цитата из Национального корпуса русского языка, см. Список литературы) ◆ Она позволяет себе петь всё: джаз и спиричуэлз, вокальные циклы, оперные арии, — и всё это с необыкновенным достоинством настоящей королевы. С. З. Спивакова, «Не всё», 2002 г. (цитата из Национального корпуса русского языка, см. Список литературы)
3. матем. в теории графов — замкнутая последовательность смежных рёбер графа ◆ Отсутствует пример употребления (см. рекомендации).
4. хим. конфигурация атомов в сложной молекуле, при которой линии связи между атомами образуют замкнутую ломаную линию ◆ Но для сложных терпеноидов, содержащих в своей структуре полизамещенные циклы, и в особенности — для среднециклических производных, стабильные конформации молекулы далеко не всегда в точности соответствуют заторможенным конформациям по всем подвижным фрагментам, и внутрициклические торсионные углы для стабильных конформаций могут принимать практически любые значения в интервале f=0-180°, в зависимости от структуры молекулы. А. Ткачёв, «Химия возобновляемого растительного сырья: исследование терпеноидов растений Сибири и Дальнего Востока» (цитата из Национального корпуса русского языка, см. Список литературы)
5. геол. последовательность смены режима накопления осадков, которая повторяется в ходе геологического развития территории ◆ Отсутствует пример употребления (см. рекомендации).
6. то же, что оборот ◆ Отсутствует пример употребления (см. рекомендации).
7. матем., теория гомологий цепь, граница которой равна 0 ◆ Отсутствует пример употребления (см. рекомендации).
8. матем. тип перестановки ◆ Отсутствует пример употребления (см. рекомендации).
9. информ. разновидность управляющей конструкции в высокоуровневых языках программирования, предназначенная для организации многократного исполнения набора инструкций; любая многократно исполняемая последовательность инструкций, организованная любым способом ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

1. частичн.: круг, оборот
2. частичн.: сборник, серия
3. —
4. —
5. осадочный цикл, седиментационный цикл
6. круг
7. —
8. —
9. —

Антонимы[править]

1. —

Гиперонимы[править]

1. последовательность

Гипонимы[править]

1. круговорот; фотоцикл; микроцикл
2. производственный цикл
3. гиперцикл
4. макроцикл, карбоцикл
5. мезоцикл, мегацикл
6. —
7. орцикл
8. —
9. —

Родственные слова[править]

Ближайшее родство
существительные: бицикл, трицикл, тетрацикл, квадроцикл, биоцикл, квазицикл, рецикл, онтоцикл, филоцикл прилагательные: циклический, цикличный, цикловый, цикловой, цикломатический

Список всех слов с корнем «-цикл-»
существительные: гетероцикл, гипоциклоида, гомоцикл, полицикл, полуцикл, цикл, циклизация, цикличность, циклоалкан, циклобутадиен, циклобутан, циклование, циклогексан, циклогексанол, циклогексанон, циклогенез, циклогераниол, циклограмма, циклограф, циклография, циклодегидратация, циклодегидрирование, циклодекстрин, циклодиализ, циклодиатермия, циклодром, циклоида, циклоинвертор, циклокаучук, циклоконденсация, циклокриотерапия, циклолиз, цикломер, циклометр,циклометрия, цикломорфоз, циклон, циклопарафин, циклопентан, циклополимер, циклополимеризация, циклоприсоединение, циклопропан, циклорама, циклорезекция, циклоскопия, циклоспорин, циклоспоровые, циклотимия, циклотрон-инжектор, циклотрон, циклотронный, циклофилин, циклофрения, эпициклоида прилагательные: алициклический, гетероциклический, гомоциклический, полициклический, полуциклический, циклизованный, цикличный, циклический, цикловой, циклографический, циклоидальный, циклоидный, циклометрический глаголы: зацикливать, зацикливаться, зациклить, зациклиться; циклизировать, циклизироваться, циклизовать, циклизоваться; цикловать, цикловаться наречия: циклически, циклично, циклографически, циклоидально

Этимология[править]

Происходит от др.-греч. κύκλος «круг; окружность» (восходит к праиндоевр. *qwel-, *qwol- «вращать», см. русск. колесо). В ряде европейских языков слово заимств. через лат. cyclus. Русск. цикл (также стар. цыклус) зафиксировано при Петре I; заимств. через польск. cykl или нем. Zyklus — то же из лат. Использованы данные словаря М. Фасмера. См. Список литературы.

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Для улучшения этой статьи желательно: Добавить примеры словоупотребления для всех значений с помощью {{пример}} Добавить все семантические связи (отсутствие можно указать прочерком, а неизвестность — символом вопроса) Добавить хотя бы один перевод для каждого значения в секцию «Перевод»

Предельный цикл — Википедия

Материал из Википедии — свободной энциклопедии

Предельный цикл — это один из возможных вариантов стационарного состояния системы в теории динамических систем и дифференциальных уравнений; предельным циклом векторного поля на фазовой плоскости или, более обобщённо, на каком-либо двумерном многообразии называется замкнутая (периодическая) траектория этого векторного поля, в окрестности которой нет других периодических траекторий. Эквивалентным является утверждение, что всякая достаточно близкая к предельному циклу траектория стремится к нему либо в прямом, либо в обратном времени.

Теоремы Пуанкаре — Бендиксона и Андронова — Понтрягина утверждают, что типичная система с непрерывным временем на плоскости (физически говоря — состояние которой задаётся двумя вещественными параметрами, скажем, напряжением и током, или положением и скоростью точки на прямой) может стремиться только к положению равновесия или к предельному циклу.

Динамика в окрестности предельного цикла[править | править код]

Как следует из определения, с каждой из сторон предельный цикл является либо отталкивающим, либо притягивающим. Если поведение с обеих сторон одинаково — цикл называется соответственно отталкивающим или притягивающим. Если же с одной стороны происходит притяжение, а с другой отталкивание — говорят о полуустойчивом цикле.

Поведение траекторий, близких к предельному циклу, описывается отображением Пуанкаре на отрезке, трансверсальном к циклу, — для этого отображения точка, соответствующая циклу, является неподвижной. Так, цикл является притягивающим или отталкивающим тогда и только тогда, когда эта точка соответственно притягивающая или отталкивающая. Цикл называется гиперболическим, если соответствующая неподвижная точка гиперболична — то есть, имеет производную, отличную от ±1{\displaystyle \pm 1}. В этом случае, если производная по модулю больше 1, цикл неустойчив, если меньше — устойчив.

Стоит отметить, что обычно — в частности, для динамики на плоскости или на сфере (вообще, исключая только случай динамики на неориентируемом многообразии) — отображение Пуанкаре сохраняет ориентацию, поэтому часто говорят просто о производной отображения Пуанкаре, не оговаривая отдельно взятие её модуля.

Гиперболические предельные циклы не разрушаются малыми возмущениями — если у исходного векторного поля был гиперболический предельный цикл, то у любого поля, C1{\displaystyle C^{1}}-близкого к нему, также найдётся близкий к исходному гиперболический предельный цикл.

Седлоузловая бифуркация[править | править код]

Наиболее простой бифуркацией, связанной с предельными циклами, является седлоузловая бифуркация: два гиперболических предельных цикла, отталкивающий и притягивающий, сближаются. В момент бифуркации они сливаются, образуя один полуустойчивый цикл, который при дальнейшем изменении параметра исчезает.

С точки зрения комплексификации (в случае аналитического векторного поля) эта бифуркация может рассматриваться как уход предельного цикла в комплексную область.

Катастрофа голубого неба[править | править код]

Однако на бутылке Клейна или при рассмотрении комплексифицированных предельных циклов возможна и более сложная бифуркация — так называемая катастрофа голубого неба. А именно, при стремлении параметра к критическому значению длина (одного!) предельного цикла начинает нарастать, стремясь к бесконечности, и поэтому он не продолжается на сам момент бифуркации.

Физический пример: осциллятор Ван дер Поля[править | править код]

Вторая часть 16-й проблемы Гильберта касается возможного количества и расположения предельных циклов полиномиальных векторных полей на плоскости. В отличие от первой — алгебраической — части, требующей описать расположение овалов алгебраической кривой заданной степени, даже для квадратичных векторных полей неизвестно существование равномерной оценки сверху на число предельных циклов.

• Каток А. Б., Хассельблат Б. Введение в современную теорию динамических систем с обзором последних достижений / Пер. с англ. под ред. А. С. Городецкого. — М.: МЦНМО, 2005. — 464 с. — ISBN 5-94057-063-1.
• Ю. С. Ильяшенко, Динамические системы и философия общности положения, М.:МЦНМО, 2007, ISBN 978-5-94057-353-1
• Yu. Ilyashenko, Centennial history of Hilbert 16th problem, Bull. Amer. Math. Soc. 39 (2002), 301-354