Циклы в с: C# и .NET | Циклы — Вебджем.рф | Создание и продвижение сайтов

Содержание

Цикл for

Очень часто возникает необходимость выполнить одну и ту же последовательность действий несколько раз: например, для вычисления выражения aⁿ необходимо выполнить n-1 раз умножение на величину a. Для этого используются циклы. В данном листочке речь пойдет о цикле for, который, как правило, используется для повторения определенной последовательности действий заданное количество раз.

Рассмотрим задачу вычисления суммы всех натуральных чисел от 1 до n. Для этого заведем переменную Sum и к ней будем прибавлять значение переменной i, где i будет принимать все значения от 1 до n. На языке C++ это можно сделать при помощи цикла for следующим образом:

int n, Sum, i;
cin >> n;
Sum = 0;
for (i = 1; i <= n; ++i)
{
    Sum = Sum + i;
}
cout << Sum << endl;

В этом примере последовательность инструкций в блоке, то есть инструкция

s = s + i будет выполнена многократно для всех значений переменной i от 1 до n, то есть в результате переменная s будет равна сумме всех натуральных чисел от 1 до n.

При использовании цикла for необходимо задать три выражения-параметра (в круглых скобках через точку с запятой).

Первый параметр – начальное значение переменной, задается в виде присваивания переменной значения, в нашем случае – i = 1. Более формально — первый параметр содержит произвольное выражение, которое вычисляется один до выполнения тела цикла, и как правило первый параметр используется для инициализации переменной цикла. Первый параметр может отсутствовать, тогда вместо него ничего не пишется, а просто ставится точка с запятой.

Второй параметр – конечное значение переменной, задается в виде условия на значение переменной, в нашем случае условие

i <= n означает, что переменная i будет принимать значения до n включительно. Более формально — второй параметр содержит произвольное выражение. Цикл будет исполняться, пока значение второго параметра истинно (или ненулевое, если это — целочисленное выражение).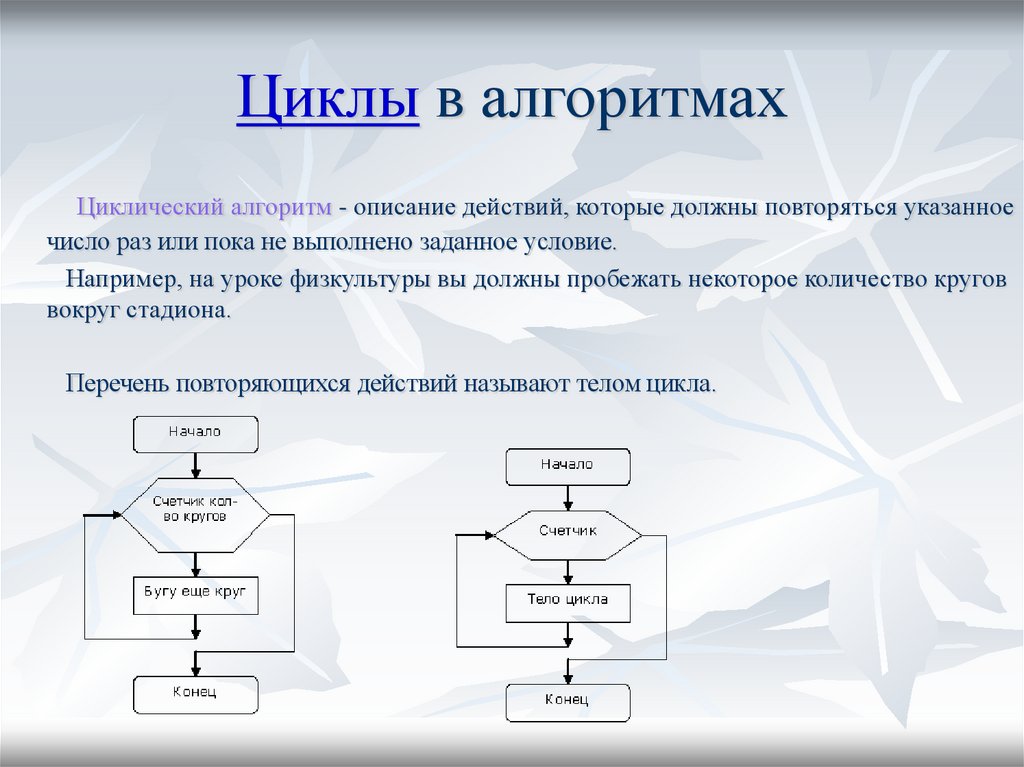

Третий параметр – шаг изменения переменной. Запись ++i равнозначна записи i = i + 1 и означает, что переменная i будет увеличиваться на 1 с каждым новым исполнением цикла, запись --i равнозначна записи i = i - 1 и означает, что переменная i будет уменьшатся на 1. Более формально, третий параметр — это произвольное выражение, которые вычисляется после выполнения тела цикла, но до проверки условия его окончания. Как правило, в третьем параметре изменяется значение переменной, записанной в первых двух параметрах. Если хочется, чтобы значение переменной в цикле менялось не на 1, а на большую величину, то это можно сделать, например, так:

i = i + 2 или i = i - 3.

В нашем примере мы могли бы сделать цикл, в котором переменная i принимала бы все значения от n до 1, уменьшаясь при этом:

for (i = n; i > 0; --i)

Циклы в Ruby— Ruby Rush

В этом уроке мы познакомимся с циклами, научимся их создавать и совершать действия с каждым элементом массива.

Мы научимся создавать с помощью конструкций while и for-in, узнаем, что такое тело цикла, а также научимся поочерёдно обрабатывать в цикле элементы массива, вводить данные с консоли и узнаем о команде break.

План урока

Что такое циклы, какие бывают, как их создавать и зачем они нужны
Работа с массивами и переменными в циклах

Что такое циклы

Если вспомнить наш образ дороги из 6-го урока, то иногда на нашей дороге машину нужно пустить по кругу. Например, если нам надо, чтобы грузовик загрузился углём в одном месте, доехал до другого и разгрузилась там и потом повторил всё это, скажем, 7 раз.

Более бытовой пример, с яйцами: вы купили в магазине десяток яиц, принесли их домой и вам нужно разложить их по специальным ячейкам на дверце вашего холодильника, для этого вам нужно будет взять каждое яйцо и положить его в нужную ячейку.

Именно для таких повторяющихся действий в программах используются циклы.

Цикл «while»

Оператор while нужен для того, чтобы сделать самый простой и универсальный цикл. Такой оператор есть в любом языке программирования.

Все, что он делает — повторяет указанный набор инструкций столько раз, сколько нужно. А сколько именно — зависит от условия цикла.

В этом смысле while очень похож на if, но в отличие от if условие будет проверяться каждый раз перед выполнением очередного повторения.

Сейчас вы все поймете на наглядном примере:

count = 1
while count <= 5 do
  puts count
  count += 1
  sleep 0.5
end
puts "я иду искать!"

Наша программа запишет в переменную count целое число 1 и приступит к циклу.

Сначала программа проверит условие (count <= 5, клювик-равно означает «меньше или равно»), которое конечно будет выполнено, ведь в count сейчас лежит 1.

Так как условие выполнено, программа «войдёт» в цикл и начнёт выполнять всё, что написано между while и end. Этот блок называется «тело цикла».

Оператор += (сложение с присваиванием)

В теле цикла появился новый для нас оператор +=:

count += 1

Это очень простая штука. Эта запись эквивалентна записи

count = count + 1

То есть, оператор += говорит «сложить текущее значение переменной с тем, что следует за мной, и записать новое значение в ту же переменную». В нашем случае за оператором идёт единица.

Итак, после выполнения действий в теле цикла в первый раз, программа выведет на экран текущее значение count (1), увеличит это значение на 1 и потом «заснёт» на полсекунды.

А после этого снова проверит условие цикла. Теперь count равен 2 и поэтому условие снова выполнится. Так будет происходить 5 раз для значений count 1,2,3,4,5 и в последнем заходе count станет равным шести, а это уже больше пяти и условие в шестой раз не выполнится.

Программа выйдет из цикла и пойдёт дальше после слова end.

И выведет на экран строчку "Я иду искать!"

Бесконечный (слепой) цикл

Будьте очень аккуратны с циклами! Если вы в предыдущей программе случайно перепутаете условие, поставив например,

while count > 0

то условие цикла всегда будет выполнено и программа будет «крутиться» вечно. Если вдруг такое произошло, чтобы выйти из программы, нажмите в консоли во время её выполнения комбинацию клавиш Ctrl+C.

Эта комбинация досрочно прерывает любую программу, которая в данный момент выполняется в командной строке (или терминале).

Цикл «for in»

Циклы очень удобны для выполнения повторяющихся операций с массивами. С массивами настолько часто работают с помощью циклов, что во многих языках придумали отдельный специальный цикл.

ОН делается с помощью конструкции «for in» и его главное предназначение — перебирать все элементы какого-нибудь массива.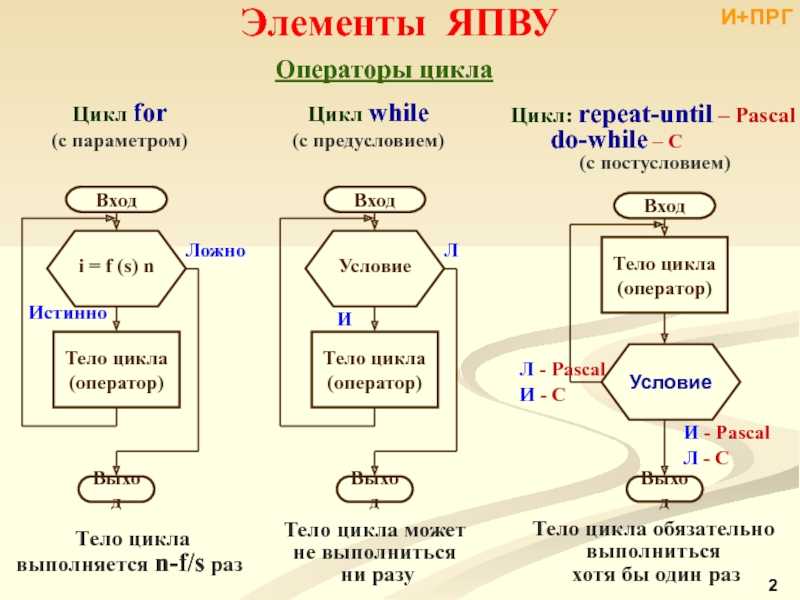

Цикл «for in» устроен следующим образом:

array = [1,2,3,4,5]
for item in array do
  puts item
end

Разберём каждое слово в этой конструкции.

Начнём с for. Это служебное слово, которое говорит программе, что мы начинаем описывать цикл, в любой программе цикл «for in» будет начинаться с этого слова.

item — это особый ярлычок, так называемая внутренняя переменная цикла. Рассматривайте ее как обычную переменную, с той важной разницей, что видна она только в теле цикла (внутри цикла). За пределами цикла она не видна (ее как будто не существует) и использовать её вне цикла нельзя.

Так же как и обычная переменная имя этой вы можете задать сами (вместо item можно написать element и т. п.).

И как для обычных переменных — следите, чтобы имя этой внутренней переменной цикла не пересекалось с другими переменными вашей программы. Будьте аккуратны с выбором названий переменных. Это общее правило для всех ваших программ.

Вернемся к нашему циклу. На каждой итерации (каждом повторении) цикл будет брать каждый элемент из массива array, и по очереди, начиная с нулевого (помним, что в массивах нумерация начинается с нуля) — записывать в переменную item этот элемент.

Следующее слово в нашем цикле тоже служебное in, после него идёт тот самый массив, элементы которого циклу предстоит поочерёдно перебирать.

И наконец, дальше идёт переменная array, в которой содержится массив. Именно из этого массива будут браться элементы для поочерёдного укладывания их в переменную item, которая в теле цикла будет выводится на экран с помощью команды puts item.

Ну и, наконец,

end заканчивает тело цикла точно также, как это было в цикле «while».

Если «перевести» это на русский язык, получится как-то так:

Для штуки в массиве
  выведи штуку
закончи

Согласитесь, довольно наглядно

Ввод данных в цикле

Продемонстрируем всю мощь циклов и массивов с помощью простого примера — сбора данных в цикле. Напишем программку «Кто такая Элис?».

Задача программы — обыграть сюжет известной песни «А кто такая Элис?»: спросить у пользователя в цикле массив имен и затем вывести поочередно эти имена в определенных фразах. Но прерваться, если встретится имя Элис и расспросить пользователя подробнее о том, кто же она такая.

https://youtube.com/watch?v=C0-4U2nTYFQ

Для начала как обычно в папке урока lesson7 создадим файлик alice.rb.

В нем создадим пустой массив

names и воспользуемся знакомыми нам по урокам 5 и 6 командами gets и push, чтобы наполнять массив данными, которые пользователь введёт с помощью консоли.

names = []
user_input = nil
while user_input != "" do
  user_input = gets.encode("UTF-8").chomp
  names << user_input
end

Как только пользователь введёт пустое имя (дважды нажмёт Enter), мы будем считать, что пользователь закончил ввод имён (это условие стоит после слова while в описании нашего цикла).

После этого мы переберём все введённые имена с помощью цикла «for in» и выведем их на экран в виде песенки:

С нами Миша
С нами Вадим
..

А если вдруг увидим слово «Элис» (именно такое условие стоит в условии оператора if), удивимся и спросим: «Элис?? Кто такая Элис?».

for item in names do
  puts "C нами " + item
  sleep 1
  if (item == "Элис")
    puts "Элис??? Кто такая Элис?"
    sleep 1
    break
  end
end
puts "Что это за девочка и где она живет?"
sleep 1
puts "А вдруг она не курит? А вдруг она не пьёт?"
sleep 1
puts "А мы с такими рожами возьмем да и припрёмся к Элис... :)"

Команда break

Обратите внимание, что в блоке «if-end» стоит команда break. Эта команда говорит программе, что пора выйти из цикла, какими бы ни были его условия.

break — очень полезная команда для досрочного выхода из цикла. Если нет возможности дождаться окончания текущей итерации, чтобы заново проверилось условие цикла.

Чтобы запустить нашу программу alice.rb, нужно перейти в вашей консоли в папку урока и запустить её с помощью привычных нам команд:

cd c:\rubytut\lesson7
ruby alice.rb

Итак, в этом уроке мы научились создавать циклы, разобрали создание циклов с помощью конструкций «while» и «for in». Научились в цикле работать с массивами, вводить данные с консоли и узнали о команде break.

В следующем уроке с использованием всех полученных ранее данных мы напишем игрушку тест на ревнивость и научимся ещё одному способу ввода данных в программу.

теория групп — Нахождение порядка произведения непересекающихся циклов в $S_n$.

Я начал с того этапа, на котором застрял в доказательстве приведенной выше леммы. Легко показать, что я только что упомянул в редактировании: $\text {Ord}\ (ab)\ \big |\ \text {lcm}\ \left (\text {Ord}\ (a), \text {Ord}\ (b) \right ).$ Чтобы доказать равенство, нужно доказать обратное, что неверно для произвольных конечных групп, даже если $a$ и $b$ коммутируют.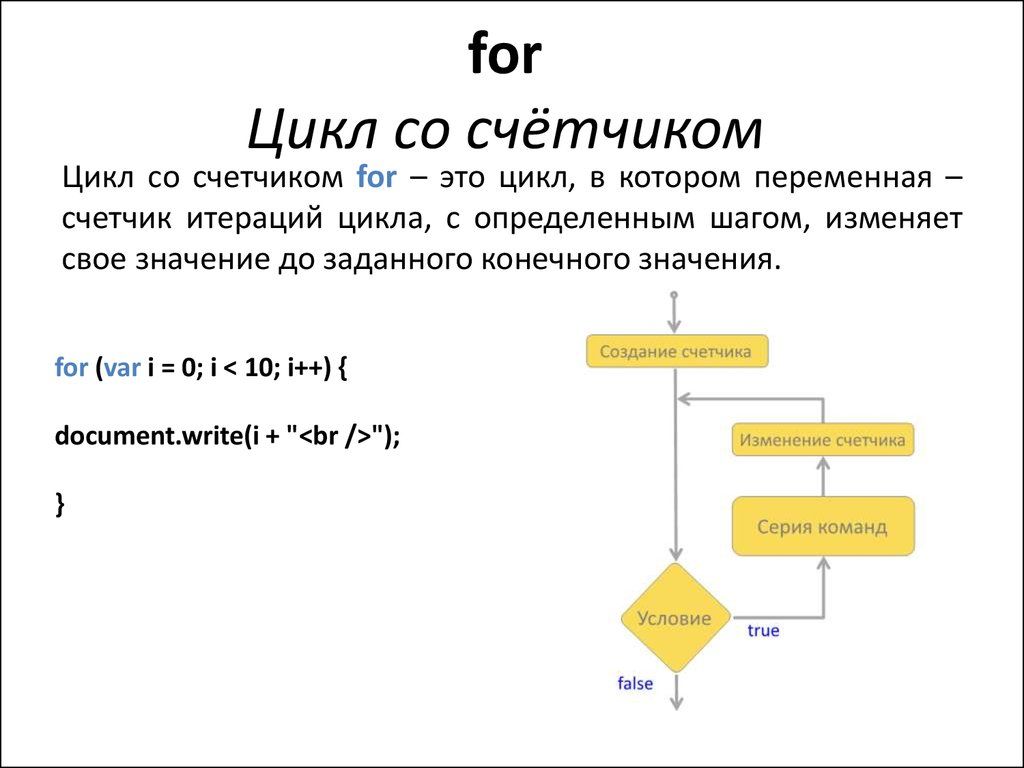 Нам так повезло, что другая часть верна для нашего случая. Почему? Давайте обсудим.

Перед доказательством требуемого результата я заметил, что если мы сможем доказать следующую лемму, мы закончим.

Лемма $:$ Пусть $\sigma, \tau \in S_n$ — два непересекающихся цикла. Тогда $\text {Ord}\ (\sigma \tau ) = \text {lcm}\ \left (\text {Ord}\ (\sigma), \text {Ord}\ (\tau) \right ).$

Для доказательства равенства в лемме введем сначала следующее определение.

Пусть $\rho = (a_1,a_2, \cdots , a_r) \in S_n$ — $r$-цикл. Тогда носитель $\rho$ обозначается $\text {Supp}\ (\rho)$ и определяется как $\text {Supp}\ (\rho) = \{a_1,a_2, \cdots , a_r \}.$ Таким образом, $\text {Supp}\ (\rho)$ состоит из тех точек в $\{1,2, \cdots, n \}$, которые возмущены операцией $\rho.$

Наблюдение $:$ Если $\rho,\rho’ \in S_n$ — два цикла, обратных друг другу, то $\text {Supp}\ (\rho) = \text {Supp}\ (\rho’ ).$ (Поскольку обратные циклы фиксируют одни и те же точки). m) = \varnothing.\ \ \ \ (*)$ 9m = \text {id}.$ Отсюда следует $\text {Ord}\ (\sigma)\ \big |\ m$ и $\text {Ord}\ (\tau)\ \big |\ m.$ Но это означает, что $\text {lcm}\ \left ( \text {Ord}\ (\sigma),\text {Ord}\ (\tau) \right )\ \bigg |\ m,$ что противоречит наше предположение, что $m < \text {lcm}\ \left (\text {Ord}\ (\sigma), \text {Ord}\ (\tau) \right ).$ Следовательно, наше предположение неверно. Итак, $m \geq \text {lcm}\ \left (\text {Ord}\ (\sigma), \text {Ord}\ (\tau) \right ).$ Но поскольку $m\ \bigg |\ \ text {lcm}\ \left (\text {Ord}\ (\sigma), \text {Ord}\ (\tau) \right )$ следует, что $m \leq \text {lcm}\ \left (\ text {Ord}\ (\sigma), \text {Ord}\ (\tau) \right ).$ Отсюда, объединяя эти два неравенства, получаем $m = \text {lcm}\ \left (\text {Ord} \ (\sigma), \text {Ord}\ (\tau) \right ).$

QED

Обозначение цикла ‣ Свойства ‣ Глава 26 Комбинаторный анализ

𝔖n обозначает множество перестановок {1,2,…,n}. σ∈𝔖n является взаимно однозначным и на отображение из {1,2,…,n} самому себе.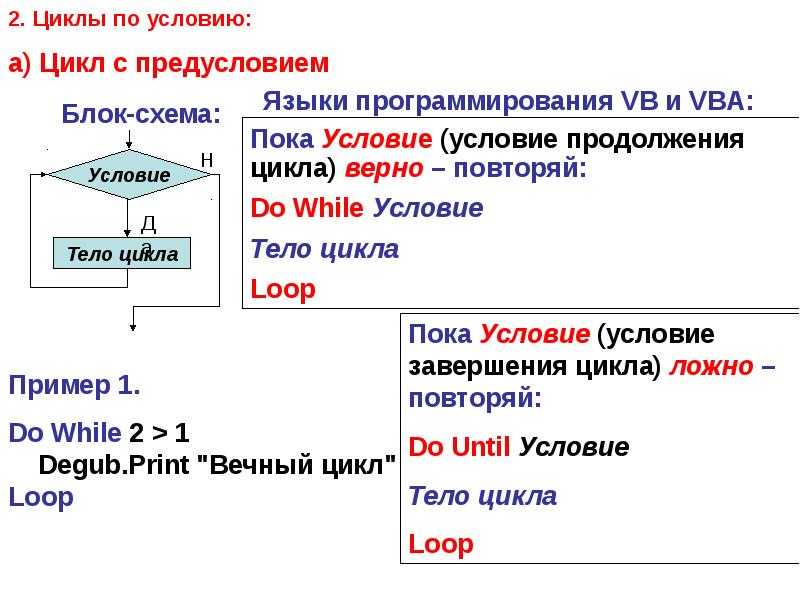 Явное представление σ может быть задано матрицей 2 × n:

26.13.1		[123⋯nσ⁡(1)σ⁡(2)σ⁡(3)⋯σ⁡(n)].

В записи цикла элементы каждого цикла заключаются в круглые скобки, упорядочены так, что σ⁡(j) следует сразу за j или, если j является последним перечисленный элемент цикла, то σ⁡(j) является первым элементом цикл. Перестановка

26.13.2		[1234567835247816]

равно (1,3,2,5,7)⁢(4)⁢(6,8) в циклической записи. Циклы длины один фиксированных точек . Они часто исключаются из обозначения цикла. В следствие, (26.13.2) также можно записать в виде (1,3,2,5,7)⁢(6,8).

Элемент 𝔖n с a1 неподвижными точками, a2 циклами длина 2,…,циклы длины n, где n=a1+2⁢a2+⋯+n⁢an, как говорят, имеет тип цикла (а1,а2,…,ан).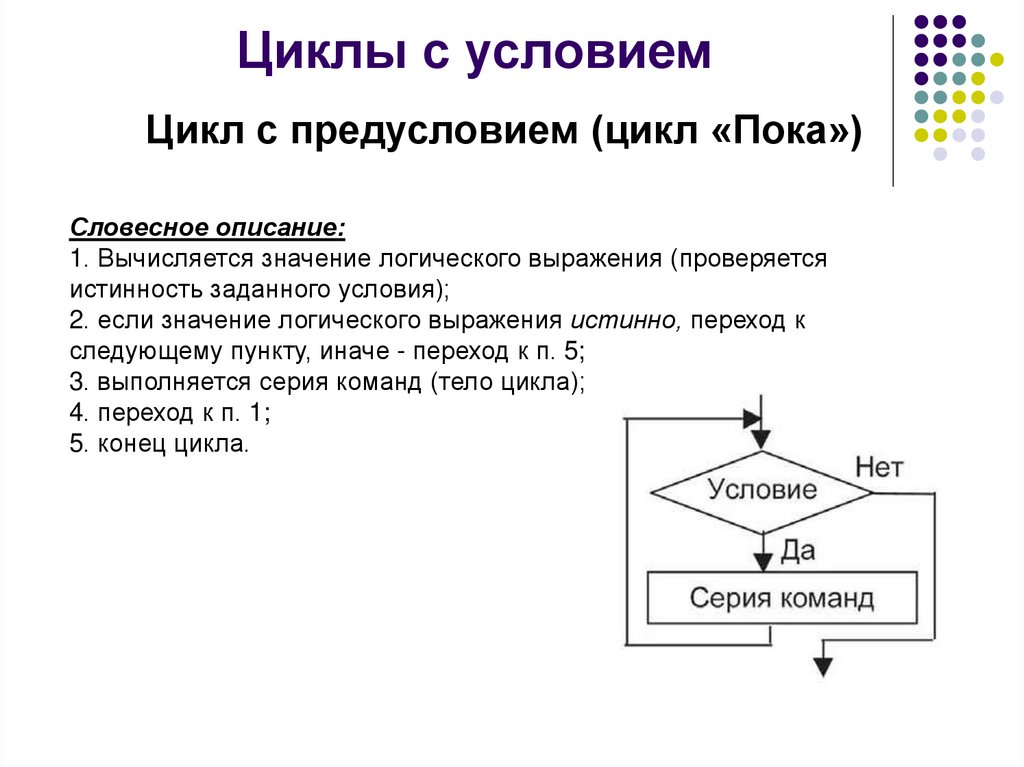 Количество элементов 𝔖n с циклическим типом (a1,a2,…,an) определяется выражением (26.4.7).

Цикл Стирлинга нумерует первого рода, обозначаемого [нк], подсчитайте количество перестановок {1,2,…,n} ровно с k циклами. Они связаны со Стирлингом. числа первого рода по

26.13.3		[nk]=\|s⁡(n,k)\|.

См. §26.8 для производящих функций, рекуррентных соотношений, тождества и асимптотические приближения.

расстройство — это перестановка без фиксированных точек. номер расстройства , d⁡(n), количество элементов 𝔖n без фиксированных точек:

26.13.4		d⁡(n)=n!⁢∑j=0n(−1)j⁢1j!=⌊n!+e−2e⌋.

Транспозиция — это перестановка, состоящая из одного цикла длина два. Смежная транспозиция представляет собой транспозицию двух последовательные целые числа. Перестановка, состоящая из одного цикла длины k можно записать как композицию k−1 двухциклов (читать справа налево). слева):

26.13.5		(j1,j2,…,jk)=(j1,j2)⁢(j2,j3)⁢⋯⁢(jk−2,jk−1)⁢(jk−1,jk).

Каждая перестановка есть произведение транспозиций. Перестановка с циклом типа (a1,a2,…,an) можно записать как произведение a2+2⁢a3+⋯+(n−1)⁢an=n−(a1+a2+⋯+an) транспозиций и не меньше. Для примера (26.13.2) это разложение определяется как (1,3,2,5,7)⁢(6,8)=(1,3)⁢(2,3)⁢(2,5)⁢(5,7)⁢(6,8 ).

Перестановка четный или нечетный в зависимости от четности количество транспозиций. Знак перестановки равен +, если перестановка четная, − если нечетная.

Каждая транспозиция является произведением смежных транспозиций. Если j

26.

Циклы в с: C# и .NET | Циклы