Деление нацело javascript: Как поделить число нацело в javascript?

Содержание

Число — JavaScript — Дока

Кратко

Секция статьи «Кратко»

Тип данных «число» (number) содержит числа с плавающей точкой в диапазоне от -(2⁵³ − 1) до 2⁵³ − 1, а также специальные значения Infinity, -Infinity и NaN.

Для этого типа данных определены стандартные арифметические операции сложения +, вычитания -, умножения *, деления /, взятия остатка от целочисленного деления %, сравнения >, <, >=, <=, ==, ===, !=, !==.

В JavaScript отсутствует отдельный тип данных для целых чисел, для целых чисел также используется тип number.

Как пишется

Секция статьи «Как пишется»

Для записи чисел используются цифры, для разделения целой и десятичной части используется точка:

const int = 4const decimal = 0. 101const sameDecimal = .101
          const int = 4
const decimal = 0.101
const sameDecimal = .101

Можно использовать экспоненциальную запись. Например, один миллион в экспоненциальной записи:

const scientific = 1e6
          const scientific = 1e6

Числа так же могут быть представлены в двоичном, восьмеричном или шестнадцатеричном виде. Такие числа начинаются с приставки 0b, 0o, 0x соответственно. При выводе на экран они будут преобразованы в десятичную систему счисления:

const binary = 0b11console.log(binary)// 3const octal = 0o77console.log(octal)// 63const hexadecimal = 0xFFconsole.log(hexadecimal)// 255
          const binary = 0b11
console.log(binary)
// 3
const octal = 0o77
console.log(octal)
// 63
const hexadecimal = 0xFF
console.log(hexadecimal)
// 255

Как понять

Секция статьи «Как понять»

Число с плавающей точкой

Секция статьи «Число с плавающей точкой»

Число в JavaScript представлено в виде 64-битного формата IEEE-754. Формат хранит произвольное число в виде трёх значений: 1 бит на знак числа, 52 бита значения числа и ещё 11 бит местоположения точки. С таким подходом можно эффективно хранить значения в большом диапазоне от -(2⁵³ − 1) до 2⁵³ − 1.

Из-за того, что положение точки в числе хранится отдельным значением, формат и называется числом с плавающей точкой (floating point number).

Проблема этого представления в том, что оно не может представить числа абсолютно точно, а только с некоторой погрешностью.

Неточные вычисления

Секция статьи «Неточные вычисления»

В десятичной системе счисления есть числа, которые не могут быть записаны точно. Например, треть ¹⁄₃ записывается как бесконечная дробь 0.33(3).

Компьютер хранит данные в двоичном виде — наборе нулей и единиц. В этой системе счисления тоже есть дроби, которые не могут быть записаны точно. В этом случае формат округляет значение до ближайшего представимого. При арифметических операциях эти неточности складываются и приводят к эффектам, подобным этому:

console. log(0.2 + 0.7)// 0.8999999999999999
          console.log(0.2 + 0.7)
// 0.8999999999999999

Это не ошибка JavaScript, а фундаментальная особенность хранения дробных чисел в памяти компьютера, с ней нужно уметь работать. Для уменьшения эффекта используется комбинация подходов — использовать как можно меньше дробных значений, а когда этого невозможно избежать — округлять числа, тем самым сбрасывая накопившийся остаток.

Например, если ваша система работает с деньгами, то лучше хранить цены в копейках или центах. Это позволит избежать большого количества операций с дробями. Для вывода цен можно пользоваться методом toFixed, который округлит число до указанного разряда:

const priceInCents = 15650const discount = priceInCents * 0.33const total = (priceInCents - discount) / 100console.log(total.toFixed(2))// 104.86
          const priceInCents = 15650
const discount = priceInCents * 0.33
const total = (priceInCents - discount) / 100
console. log(total.toFixed(2))
// 104.86

Похожую проблему можно наблюдать при сравнении очень маленьких и очень больших чисел. В таких случаях из-за округления точность теряется и различные числа компьютер представляет одинаковыми:

const small = 0.11111111111111111const smaller = 0.11111111111111110console.log(small.toFixed(20))// 0.11111111111111110494console.log(smaller.toFixed(20))// 0.11111111111111110494console.log(small === smaller)// true
          const small = 0.11111111111111111
const smaller = 0.11111111111111110
console.log(small.toFixed(20))
// 0.11111111111111110494
console.log(smaller.toFixed(20))
// 0.11111111111111110494
console.log(small === smaller)
// true

Специальные значения

Секция статьи «Специальные значения»

Стандарт IEEE-754 определяет три специальных значения. Эти значения принадлежат типу number, но не работают, как обычные числа:

бесконечность Infinity;
минус бесконечность -Infinity;
не число (not a number) NaN.

Бесконечности используются, чтобы определить результат некоторых арифметических операций. Например, деление на ноль в JavaScript вернёт бесконечность:

console.log(5 / 0)// Infinityconsole.log(-3 / 0)// -Infinity
          console.log(5 / 0)
// Infinity
console.log(-3 / 0)
// -Infinity

Если попытаться создать число, которое находится вне диапазона доступных чисел, результатом будет тоже бесконечность:

console.log(1e999)// Infinity
          console.log(1e999)
// Infinity

Значение NaN используется, чтобы сообщить об операции, результатом которой оказалось не число. В JavaScript существует пять операций, которые могут вернуть NaN:

ошибка парсинга числа (например, при попытке превратить строку в число parseInt('привет')).
результат математической операции не находится в полей действительных чисел (например, взятие корня от -1).
один из операндов в арифметической операции — NaN (5 + NaN).
результат арифметической операции не определён для переданных операндов (undefined + undefined).
арифметическая операция со строкой, кроме сложения ('привет' * 5)

Согласно спецификации, NaN не равен самому себе. Проверить, что в переменной хранится NaN простым сравнением не получится:

const result = NaNconsole.log(result === NaN)// false
          const result = NaN
console.log(result === NaN)
// false

Для проверки на NaN пользуйтесь функцией Number.isNaN()

, которая возвращает true если переданное значение — NaN:

const result = NaNconsole.log(Number.isNaN(result))// true
          const result = NaN
console.log(Number. isNaN(result))
// true

Для проверки, что значение в переменной является конечным числом, а не специальным значением, пользуйтесь функцией Number.isFinite(), она возвращает true, если переданный аргумент — число.

const inf = Infinityconst nan = NaNconst num = 99999console.log(Number.isFinite(inf))// falseconsole.log(Number.isFinite(nan))// falseconsole.log(Number.isFinite(num))// true
          const inf = Infinity
const nan = NaN
const num = 99999
console.log(Number.isFinite(inf))
// false
console.log(Number.isFinite(nan))
// false
console.log(Number.isFinite(num))
// true

Операции с числами

Секция статьи «Операции с числами»

С числами можно выполнять стандартные математические операции, для определения приоритета операций пользуются скобками:

const a = 5const b = 10console.log(-a)// -5console.log(a + b)// 15console.log(a - b)// -5console. log(a / b)// 0.5console.log(a * b)// 50console.log((a + b) / 10)// 1.5
          const a = 5
const b = 10
console.log(-a)
// -5
console.log(a + b)
// 15
console.log(a - b)
// -5
console.log(a / b)
// 0.5
console.log(a * b)
// 50
console.log((a + b) / 10)
// 1.5

Существует оператор взятия остатка от деления нацело %:

console.log(5 % 2)// 1, потому что 5 = 2 * 2 + 1console.log(5 % 3)// 2, потому что 5 = 1 * 3 + 2console.log(5 % 5)// 0, потому что 5 = 5 * 1 + 0
          console.log(5 % 2)
// 1, потому что 5 = 2 * 2 + 1
console.log(5 % 3)
// 2, потому что 5 = 1 * 3 + 2
console.log(5 % 5)
// 0, потому что 5 = 5 * 1 + 0

Возведения в степень **:

console.log(2 ** 4)// 16
          console.log(2 ** 4)
// 16

Для округления, взятия корней и других математических операций в JavaScript существует отдельный модуль Math.

Операторы сравнения, возвращают булевое значение:

console. log(5 > 10)// falseconsole.log(5 >= 10)// falseconsole.log(5 < 10)// trueconsole.log(10 <= 10)// trueconsole.log(5 == 10)// falseconsole.log(5 === 10)// falseconsole.log(5 != 10)// trueconsole.log(5 !== 10)// true
          console.log(5 > 10)
// false
console.log(5 >= 10)
// false
console.log(5 < 10)
// true
console.log(10 <= 10)
// true
console.log(5 == 10)
// false
console.log(5 === 10)
// false
console.log(5 != 10)
// true
console.log(5 !== 10)
// true

☝️

Строгое === и нестрогое == сравнение работает одинаково, когда оба сравниваемых значения имеют тип «число». В других случаях их поведение отличается.

Числовой разделитель

Секция статьи «Числовой разделитель»

В спецификации EcmaScript 2021 года (ES12) появилась возможность добавлять в числа разделители. Например:

const number = 1_000_000_000console.log(number)// 1000000000
          const number = 1_000_000_000
console. log(number)
// 1000000000

Разделители делают большие числа более читаемыми, внешне выделяя разряды чисел.

const integer = 1_234_567_890const float = 0.123_456_789
          const integer = 1_234_567_890
const float = 0.123_456_789

Разделители доступны для чисел других счислений и BigInt:

const binary = 0b0101_1111_0001const hex = 0x12_AB_34_CDconst bigInt = 1_234_567_890n
          const binary = 0b0101_1111_0001
const hex = 0x12_AB_34_CD
const bigInt = 1_234_567_890n

Дополнительные методы

Секция статьи «Дополнительные методы»

Сам по себе примитивный тип «число» не имеет методов. Когда происходит вызов метода у числа, оно автоматически оборачивается в специальную обёртку, которая и содержит методы:

const num = 99.99console.log(num.toFixed(1))// 100.0
          const num = 99.99
console.log(num.toFixed(1))
// 100.0

Часто используемые методы обёртки, такие как toFixed(), toString() и toLocaleString(), описаны в отдельной статье.

На собеседовании

Секция статьи «На собеседовании»

Это партнёрская рубрика, мы выпускаем её совместно с сервисом онлайн-образования Яндекс Практикум. Приносите вопрос, на который не знаете ответа, в задачи, мы разложим всё по полочкам и опубликуем. Если знаете ответ, присылайте пулреквест на GitHub.

❓

Как проверить, что значение переменной (например, possiblyWrongNumber) не является NaN? Предполагаем что typeof possiblyWrongNumber === 'number'

Секция статьи «Как проверить, что значение переменной (например, possiblyWrongNumber) не является NaN? Предполагаем что typeof possiblyWrongNumber === ‘number'»

Редакция

Полина Гуртовая отвечает

Секция статьи «Редакция Полина Гуртовая отвечает»

Ответ очень простой – нужно воспользоваться специальной функцией Number. isNan(). В качестве аргумента нужно передать проверяемую переменную.

Вас может запутать формулировка вопроса: typeof possiblyWrongNumber === 'number'. Это же not a number, подумаете вы. Дело в том, что NaN используется для обозначения результатов вычислений, в которых «что-то пошло не так». Можете думать о NaN так: «Тут должно быть число, но вычисление сломалось». Это может произойти, если захотите вычислить квадратный корень из -1. В результате получится комплексное число, с которым наш браузер из коробки работать не умеет.

Неправильным ответом на этот вопрос будет вот такая проверка:

possiblyWrongNumber === NaN
          possiblyWrongNumber === NaN

Однако в ней уже содержится ответ на более хитрый дополнительный вопрос:

❓ Представим себе, что функции Number. isNan() не существует. Как в таком случае проверить, что значение переменной 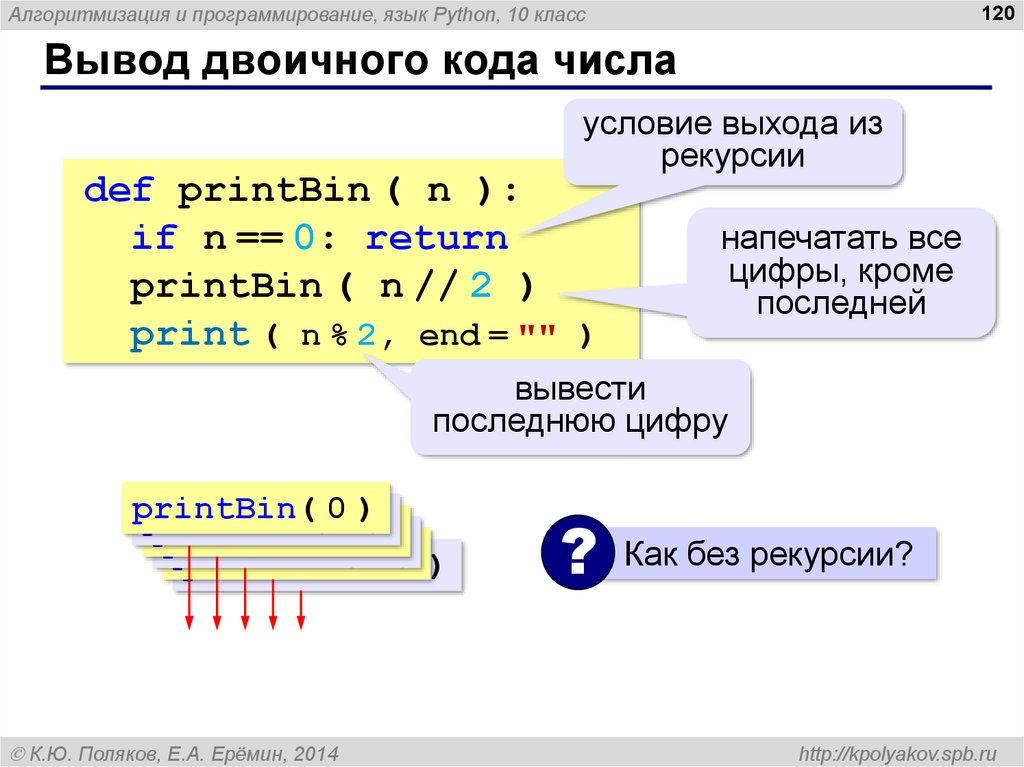possiblyWrongNumber не является NaN? Условие typeof possiblyWrongNumber === 'number' по-прежнему выполняется.

Ответ такой: просто нужно сравнить значение переменной possiblyWrongNumber с самим собой. Если они равны, значит в переменной не NaN:

possiblyWrongNumber === possiblyWrongNumber
          possiblyWrongNumber === possiblyWrongNumber

Сумма цифр трехзначного числа. Решение задачи на Python

Вводится трехзначное число. Написать программу, которая вычисляет сумму его цифр.

(Это задача на линейные алгоритмы, если требуется найти сумму цифр числа произвольной длины с помощью цикла см. задачу «Сумма и произведение цифр числа».)

Например, если было введено 349, программа должна вывести на экран число 16, так как 3 + 4 + 9 = 16.

Как извлечь отдельные цифры из числа? Если число разделить нацело на десять, в остатке будет последняя цифра этого числа. Например, если 349 разделить нацело на 10, то получится частное 34 и остаток 9. Если потом 34 разделить также, получится частное 3 и остаток 4; далее при делении 3 на 10 получим частное 0 и остаток 3.

В языках программирования почти всегда есть две операции:

1) нахождение целого при делении нацело,

2) нахождение остатка при делении нацело.

В языке программирования Python первая операция обозначается // (двумя знаками деления), а вторая — % (знаком процента). Например:

>>> 34 // 10
3
>>> 34 % 10
4

Примечание. Операции деления нацело и нахождения остатка с точки зрения арифметики применимы только к целым числам.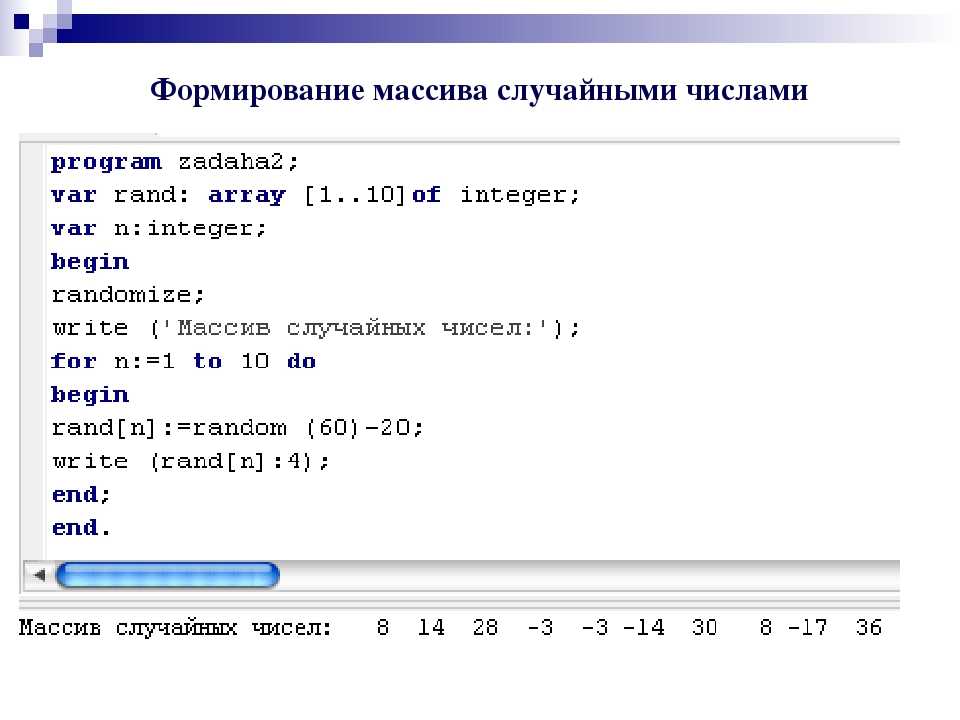 Но в Python их можно использовать и по отношению к дробным числам:

>>> 34.5 % 10
4.5
>>> 34.5 // 10
3.0
>>> 34.5 // 12.9
2.0

Алгоритм нахождения суммы цифр трехзначного числа abc (где a — сотни, b — десятки и c — единицы) можно описать так:

Найти остаток от деления abc на 10, записать его в переменную d1. Это будет цифра c.
Избавиться от цифры c в числе abc, разделив его нацело на 10.
Найти остаток от деления ab на 10, записать его в переменную d2. Это будет цифра b.
Избавиться от цифры b в числе ab, разделив его нацело на 10.
Число a однозначное. Это еще одна цифра исходного числа.
Сложить оставшееся число a со значениями переменных d1 и d2.

n = input("Введите трехзначное число: ")
n = int(n)
 
d1 = n % 10
n = n // 10
d2 = n % 10
n = n // 10
 
print("Сумма цифр числа:", n + d2 + d3)

Пример выполнения программы:

Введите трехзначное число: 742
Сумма цифр числа: 13

Однако, если нам известно, что число состоит из трех разрядов (цифр), есть немного другой способ извлечения цифр из числа:

Остаток от деления на 10 исходного числа дает последнюю цифру числа.
Если найти остаток от деления на 100 исходного числа, то мы получи последние две цифры числа. Далее следует разделить полученное двухзначное число нацело на 10, и у нас окажется вторая цифра числа.
Если исходное трехзначное число разделить нацело на 100, то получится первая цифра числа.

n = input("Введите трехзначное число: ")
n = int(n)
 
d1 = n % 10
d2 = n % 100 // 10
d3 = n // 100
 
print("Сумма цифр числа:", d1 + d2 + d3)

В Python данную задачу можно решить без использования арифметических действий, а путем извлечения из исходной строки отдельных символов с последующим их преобразованием к целому.

n = input("Введите трехзначное число: ")
 
# Извлекается первый[0] символ строки, 
# преобразуется к целому.
# Аналогично второй[1] и третий[2].
a = int(n[0])
b = int(n[1])
c = int(n[2])
 
print("Сумма цифр числа:", a + b + c)

Задача может быть усложнена тем, что число вводится не пользователем с клавиатуры, а должно быть сгенерировано случайно. Причем обязательно трехзначное число.

В этом случае надо воспользоваться функциями randint(), randrange() или random() из модуля random. Первым двум функциям передаются диапазоны: randint(100, 999), randrange(100, 1000). Получить трехзначное число, используя random() немного сложнее:

# Функция random генерирует
# случайное дробное число от 0 до 1
from random import random
 
# При умножении на 900 получается случайное
# число от 0 до 899.(9).
# Если прибавить 100, то получится
# от 100 до 999.(9).
n = random() * 900 + 100
 
# Отбрасывается дробная часть, 
# число выводится на экран
n = int(n)
print(n)
 
# Извлекается старший разряд числа
# путем деления нацело на 100
a = n // 100
 
# Деление нацело на 10 удаляет 
# последнюю цифру числа.
# Затем нахождение остатка при 
# делении на 10 извлекает последнюю цифру,
# которая в исходном числе была средней.
b = (n // 10) % 10
 
# Младший разряд числа находится
# как остаток при делении нацело на 10. 
c = n % 10
 
print(a+b+c)

Больше задач в PDF

javascript — Как убедиться, что целочисленное деление дает правильные результаты?

Задавать вопрос

спросил 7 лет, 2 месяца назад

Изменено 2 года, 9 месяцев назад

Просмотрено 1к раз

Я знаю, что вычисления с плавающей запятой могут быть неточными. Например:

 вар х = 100*0,333;

Здесь x устанавливается равным 33.300000000000004 , а не 33 . Это может показаться незначительной проблемой, но становится серьезной, если используется округление. Например, Math.ceil(x) будет неправильным — вместо 33 будет получено 34 .

Проблема в том, что мне сказали, что JS не делает большой разницы между целыми числами и числами с плавающей запятой. Поэтому я начинаю беспокоиться, есть ли способ убедиться в правильности интегрального деления.

Обычная формула целочисленного деления в JS выглядит так: Math.floor(n/m) , где n , m — целые числа. Теперь допустим, что м делит на поровну. Поскольку JS обрабатывает каждое число как число с плавающей запятой, n/m вернет число с плавающей запятой. Если это число с плавающей запятой не является точным, но даже немного меньше фактического результата вычисления, то Math.floor(n/m) будет округлено до одного целого числа меньше, чем должно.

Для иллюстрации: если, например, 9/3 дает 2.999999999999999 , а не 3 , то Math.floor(9/3) неправильно даст 1.3 3 2 89018 Ну, на самом деле, Math.floor(9/3) действительно выдает правильные результаты, но это, конечно, только пример; замените 9 и 3 любым неудачным выбором целых чисел.

Может ли случиться такой сценарий? Если да, то есть ли способ обеспечить правильные результаты?

javascript
точность с плавающей запятой
целочисленное деление

Может ли случиться такой сценарий?

Нет. Если это целые числа (т.е. числа с плавающей запятой без дробной части) и делятся нацело, то результат будет точным и снова целым числом.
Если делить не нацело, результат всегда будет больше, чем точный результат целочисленного деления. Вы никогда не получите 2.9999999… номер, который должен был быть 3 . Результаты с плавающей запятой настолько точны, насколько это возможно, округление не разрушает общий предварительный порядок.

, если вы хотите получить точный результат целочисленного деления. Затем сделайте это

 Math. round((m - m%n)/n)

Если значение деления двух чисел должно быть 3, то так и будет. Если значение должно быть 2,999999999999, оно будет таким. Java не делает какого-то странного скрытого округления вверх или вниз. Если вам ВСЕГДА нужно округлить значение в меньшую сторону, используйте Floor (x/y), даже если значение равно 2,9.99999999999999999999999999999999999 он все равно вернется как 2. Вот что делает Флор. То же самое и с потолком. если значение равно 3.0000000000000000000001, то оно будет установлено на 4. Я учу этому в колледже, так оно и должно работать, и оно работает.

Зарегистрируйтесь или войдите

Зарегистрироваться с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Целочисленная математика в JavaScript | Джеймс Дарпиниан

Возможно, вы знаете, что все числа в JavaScript являются 64-битными значениями с плавающей запятой двойной точности. Иногда это удобно, и это работает довольно хорошо по умолчанию для начинающих программистов, которых часто смущает целочисленная математика, и это справедливо, когда 1 / 2 = 0 . К сожалению, это замедляет работу. Двойники занимают много памяти, а математика с плавающей запятой медленнее, чем математика с целыми числами на процессорах. Это также неудобно, если вы хотите перенести существующий код на JavaScript, потому что существующий код обычно предполагает использование целочисленной математики.

К счастью, есть способ заставить JavaScript выполнять целочисленные вычисления, и он работает на удивление хорошо!

TL;DR

Добавить | 0 после каждой математической операции для получения 32-битного целого числа со знаком и >>> 0 для 32-битного целого числа без знака. И храните все свои числа в типизированных массивах вместо массивов JavaScript.

Фон

В JavaScript есть полный набор инструкций по обработке битов. Побитовые операторы и/или/xor/not/shift такие же, как в C, и я понятия не имею, почему они изначально были в JavaScript, потому что они не кажутся очень полезными для веб-разработки. Кроме того, это странно, когда все числа имеют двойную точность с плавающей запятой, верно? Никто не выполняет побитовые операции над числами с плавающей запятой. И JavaScript тоже. На самом деле, JavaScript (концептуально) сначала округлит ваш 64-битный тип double до 32-битного целого числа со знаком, выполнит побитовую операцию, а затем преобразует его обратно в значение двойной точности. Странный!

Все эти преобразования звучат дорого! И, вероятно, так оно и было, еще до asm.js. Разработчики asm.js переносили код C на JavaScript, и странное приведение типов, выполняемое странными побитовыми операторами JavaScript, было как раз тем, что им было нужно для эмуляции целочисленной арифметики C.

Хитрость

Если в C x и y являются целыми числами, то x / y будет выполнять целочисленное деление, округляя результат в меньшую сторону. В JavaScript x/y всегда будет делением с плавающей запятой с результатом с плавающей запятой. Но если вы примените побитовый оператор сразу после этого, то результат будет округлен в меньшую сторону, преобразован в целое число, и вы получите то же число, что и C! С большим количеством работы. Конечно, вы не хотите, чтобы ваш побитовый оператор изменил результат, поэтому вы можете выполнить побитовую операцию без операций, например >> 0 или | 0 . No-op в C, конечно, но не в JavaScript из-за целочисленного преобразования.

Как только asm.js начал делать | 0 везде, люди начали очень интересоваться его оптимизацией. Очевидно, что вы можете просто пропустить выполнение инструкции ИЛИ , так как она ничего не делает. Но настоящая работа заключается во всех этих медленных преобразованиях в числа с плавающей запятой и обратно. Получается, что если добавить | 0 после каждой операции ваш JIT-компилятор JavaScript также может пропускать избыточные преобразования и просто все время сохранять ваши числа как целые числа. Когда известно, что входные данные для деления являются целыми числами, и | 0 снова преобразует его в целое число, затем вместо двух преобразований в число с плавающей запятой, инструкции деления с плавающей запятой, а затем преобразования в целое число, JIT может выдать одну команду целочисленного деления, как это сделал бы компилятор C, без вообще изменить результат. Это довольно чудесно!

Подробнее

Все побитовые операторы JavaScript, унаследованные от C, преобразуют свои операнды и результаты в 32-битные целые числа со знаком. Но есть трюк и для целых чисел без знака. В JavaScript есть один дополнительный побитовый оператор, которого нет в C: >>> . По сути, это оператор «беззнакового сдвига вправо», и он особенный, поскольку его результатом является 32-разрядное целое число без знака. Поэтому, когда вам нужно целое число со знаком, вы добавляете | 0 после ваших арифметических операций, а для беззнаковых вы используете >>> 0 .

Все это прекрасно работает для 32-битных целочисленных вычислений, как со знаком, так и без знака. А другие размеры? К сожалению, если вам нужна 64-битная целочисленная математика, вам не повезло. Эти трюки работают для 32-битных чисел, потому что с плавающей запятой двойной точности можно точно представить каждое 32-битное целое число, и выполнение деления с плавающей запятой двух целых чисел меньше 2 ³², а затем преобразование результата в целое число дает точно такой же результат, как инструкция целочисленного деления в каждом случае. Но полный диапазон 64-битных целых чисел не может быть представлен с плавающей запятой двойной точности. Целые числа, превышающие 2 ⁵³, могут быть представлены неточно, и числа JavaScript всегда должны вести себя так, как если бы они были представлены значениями с плавающей запятой двойной точности, даже если это не так. Компилятор JIT не может просто незаметно выполнять 64-битные целочисленные вычисления и притворяться, что это числа с плавающей запятой, потому что он получит другие результаты, когда целые числа достаточно велики.

К сожалению, умножение двух 32-битных чисел может дать результат до 2 ⁶⁴ . Когда результат больше 2 ⁵³, умножение двойной точности с плавающей запятой может давать ответы, отличные от умножения целых чисел, даже если оно впоследствии усекается до 32-битного целого числа. Это не позволяет JavaScript JIT использовать инструкции целочисленного умножения. Для решения этой проблемы был введен Math.imul() . Поэтому для целочисленного умножения вы должны использовать это вместо * оператор, за которым следует | 0 .

ОК, 64-битная версия не работает, как насчет 16-битной и 8-битной? Ну, с одной стороны, вы тоже не можете этого сделать, вся ваша целочисленная математика будет иметь ширину 32 бита. Но, с другой стороны, это не так уж и плохо, потому что ЦП складывает 32-битные числа так же быстро, как и 8-битные. Там, где меньшие типы действительно , дело в использовании памяти. Если вам нужен массив байтов, но вместо этого вы используете массив JavaScript для хранения чисел JavaScript, он будет использовать в 8 раз больше памяти (и в 8 раз больше пропускной способности памяти, и в 8 раз больше места в кэше), потому что каждое число JavaScript составляет 8 байтов. К счастью, в JavaScript есть решение и для этого: типизированные массивы. Типизированные массивы могут содержать 8-битные, 16-битные и 32-битные значения как со знаком, так и без знака. Дополнительным преимуществом является то, что, поскольку типизированные массивы не могут содержать ссылки на объекты, сборщику мусора не нужно сканировать их содержимое, что также повышает производительность.

Дополнительный вопрос: как насчет 32-битной плавающей запятой? Это быстрее, чем 64-битные вычисления с плавающей запятой, и часто используется в 3D-графике. Можем ли мы использовать аналогичный трюк, чтобы JIT-компилятор JavaScript выдавал 32-битные математические инструкции с плавающей запятой? Ответ — да, есть функция Math.fround , используемая для этой цели asm.js. Я никогда не пробовал использовать его сам.

Собираем все вместе

Asm.js использует эти методы для преобразования кода C в JavaScript и приближается к производительности собственных компиляторов C.

Число — JavaScript — Дока

Кратко

Как пишется

Как понять

Число с плавающей точкой

Неточные вычисления

Специальные значения

Операции с числами

Числовой разделитель

Дополнительные методы

На собеседовании

Редакция

Сумма цифр трехзначного числа. Решение задачи на Python

javascript — Как убедиться, что целочисленное деление дает правильные результаты?

Зарегистрируйтесь или войдите

Опубликовать как гость

Опубликовать как гость

Целочисленная математика в JavaScript | Джеймс Дарпиниан

TL;DR

Фон

Хитрость

Подробнее

Собираем все вместе

Добавить комментарий Отменить ответ

Рубрики

Деление нацело javascript: Как поделить число нацело в javascript?

Число — JavaScript — Дока

Кратко

Как пишется

Как понять

Число с плавающей точкой

Неточные вычисления

Специальные значения

Операции с числами

Числовой разделитель

Дополнительные методы

На собеседовании

Редакция

Сумма цифр трехзначного числа. Решение задачи на Python

javascript — Как убедиться, что целочисленное деление дает правильные результаты?

Зарегистрируйтесь или войдите

Опубликовать как гость

Опубликовать как гость

Целочисленная математика в JavaScript | Джеймс Дарпиниан

TL;DR​

Фон

Хитрость

Подробнее

Собираем все вместе

Добавить комментарий Отменить ответ

Рубрики

TL;DR