Длина высоты: Все формулы высоты треугольника

Высота треугольника

Урок содержит описание свойств и формулы нахождения высоты треугольника, а также примеры решения задач. Если Вы не нашли решение подходящей задачи — пишите про это на форуме. Наверняка, курс будет дополнен. 

ВЫСОТА ТРЕУГОЛЬНИКА Высота треугольника – опущенный из вершины треугольника перпендикуляр, проведенный на противолежащую вершине сторону или на ее продолжение. Свойства высоты треугольника: Если в треугольнике две высоты равны, то такой треугольник — равнобедренный В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащих на двух сторонах, непараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины этой стороны всегда можно провести окружность В остроугольном треугольнике две его высоты отсекают от него подобные треугольники Минимальная высота в треугольнике всегда проходит внутри этого треугольника Ортоцентр треугольника Все три высоты треугольника (проведенные из трех вершин) пересекаются в одной точке, которая называется ортоцентром. Для того, чтобы найти точку пересечения высот, достаточно провести две высоты (две прямые пересекаются только в одной точке). Расположение ортоцентра (точка О) определяется видом треугольника. У остроугольного треугольника точка пересечения высот находится в плоскости треугольника. (Рис.1). У прямоугольного треугольника точка пересечения высот совпадает с вершиной прямого угла (Рис.2). У тупоугольного треугольника точка пересечения высот находится за плоскостью треугольника (Рис. 3). У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают. У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

ВИСОТА ТРИКУТНИКА Висота трикутника — опущений з вершини трикутника перпендикуляр, проведений на протилежну вершині бік або на її продовження. Всі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром. Для того, щоб знайти точку перетину висот, досить провести дві висоти (дві прямі перетинаються тільки в одній точці). Розміщення ортоцентра (точка О) визначається видом трикутника. У гострокутного трикутника точка перетину висот знаходиться в площині трикутника. (Мал.1). У прямокутного трикутника точка перетину висот збігається з вершиною прямого кута (Мал.2). У тупоугольного трикутника точка перетину висот знаходиться за площиною трикутника (Мал.3). У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються. У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються.

 

Формулы нахождения высоты треугольника

Рисунок приведен для облегчения восприятия формул нахождения высоты треугольника. Общее правило — длина стороны обозначена маленькой буквой, лежащей напротив соответствующего угла. То есть сторона a лежит напротив угла A.
Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена.

Другие обозначения:
a,b,c — длины сторон треугольника
h_a — высота треугольника, проведенная к стороне a из противолежащего угла
h_b — высота, проведенная к стороне b
h_c — высота, проведенная к стороне c
R — радиус описанной окружности
r — радиус вписанной окружности

Пояснения к формулам.
Высота треугольника равна произведению длины стороны, прилежащей к углу, из которой опущена эта высота на синус угла между этой стороной и стороной, на которую такая высота опущена (Формула 1)
Высота треугольника равна частному от деления удвоенной величины площади треугольника на длину стороны, к которой опущена эта высота (Формула 2)
Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).

Высоты сторон в треугольнике соотносятся между собой в той же самой пропорции, как соотносятся между собой обратные пропорции длин сторон этого же треугольника, а также в той же самой пропорции между собой относятся произведения пар сторон треугольника, которые имеют общий угол (Формула 5). 
Сумма обратных значений высот треугольника равна обратному значению радиуса вписанной в такой треугольник окружности (Формула 6)
Площадь треугольника можно найти через длины высот этого треугольника (Формула 7)
Длину стороны треугольника, на которую опущена высота, можно найти через применение формул 7 и 2.

В прямоугольном треугольнике ABC (угол C = 90⁰) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см

Решение.

Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).

Прямоугольные треугольники — единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.

Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)

Треугольники ABC и CBD подобны. Значит:

AD/DC = DC/BD, то есть

DC²=AD*BD

DC²=9*16

DC=12 см

Задача на применение теоремы Пифагора. 

Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см.  Разность отрезков BD-AD=5 см. 

Найти: Стороны треугольника ABC. 

Решение.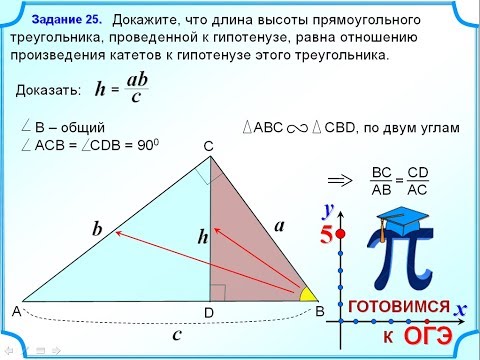  

1.Составим систему уравнений согласно теореме Пифагора

CD²+BD²=BC²

CD²+AD²=AC²

поскольку CD=6

36+BD²=BC²

36+AD²=AC²

Поскольку BD-AD=5, то

BD = AD+5, тогда система уравнений принимает вид

36+(AD+5)²=BC²

36+AD²=AC²

Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой — равенство не будет нарушено. Получим: 

36+36+(AD+5)²+AD²=AC²+BC²

72+(AD+5)²+AD²=AC²+BC²

2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:

AC²+BC²=AB²

Поскольку AB=BD+AD, уравнение примет вид: 

AC²+BC²=(AD+BD)²

Поскольку BD-AD=5, то BD = AD+5, тогда

AC²+BC²=(AD+AD+5)² 

3.  Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:

72+(AD+5)²+AD²=AC²+BC²

AC²+BC²=(AD+AD+5)²

Они имеют общую часть AC²+BC² . Таким образом, приравняем их друг к другу.

72+(AD+5)²+AD²=(AD+AD+5)²

72+AD²+10AD+25+AD²=4AD²+20AD+25

-2AD²-10AD+72=0 

В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:

х₁=-3,5

x₂=4 

Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.

AD=4

Соответственно

BD = AD + 5 = 9

AB = BD + AD = 4 + 9 = 13

По теореме Пифагора находим остальные стороны треугольника:

AC = корень из (52)

BC = корень из (117).

0  

 Треугольник (Трикутник) | Описание курса | Сумма углов треугольника 

   

Уравнение высоты треугольника

Длина сторон треугольника:
|AB| = 15
|AC| = 11.18
|BC| = 14.14
Расстояние d от точки M: d = 10
Даны координаты вершин треугольника: A(-5,2), B(7,-7), C(5,7).
2) Длина сторон треугольника
Расстояние d между точками M₁(x₁; y₁) и M₂(x₂; y₂) определяется по формуле:




8) Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями:

Уравнение прямой AB
Каноническое уравнение прямой: или
или y = ^-3/₄x ^-7/₄ или 4y + 3x +7 = 0
Уравнение прямой AC
Каноническое уравнение прямой: или
или y = ¹/₂x + ⁹/₂ или 2y -x — 9 = 0
Уравнение прямой BC
Каноническое уравнение прямой: или
или y = -7x + 42 или y + 7x — 42 = 0
3) Угол между прямыми
Уравнение прямой AB:y = ^-3/₄x ^-7/₄
Уравнение прямой AC:y = ¹/₂x + ⁹/₂
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k₁x + b₁ и y₂ = k₂x + b₂, вычисляется по формуле:

Угловые коэффициенты данных прямых равны ^-3/₄ и ¹/₂. Воспользуемся формулой, причем ее правую часть берем по модулю:

tg φ = 2
φ = arctg(2) = 63.44⁰ или 1.107 рад.
9) Уравнение высоты через вершину C
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:


y = ⁴/₃x + ¹/₃ или 3y -4x — 1 = 0
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB.
Уравнение AB: y = ^-3/₄x ^-7/₄, т.е. k₁ = ^-3/₄
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1.
Подставляя вместо k₁ угловой коэффициент данной прямой, получим :
^-3/₄k = -1, откуда k = ⁴/₃
Так как перпендикуляр проходит через точку C(5,7) и имеет k = ⁴/₃,то будем искать его уравнение в виде: y-y₀ = k(x-x₀).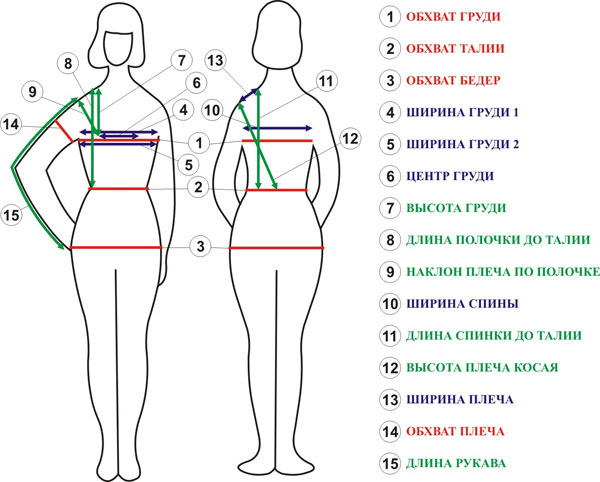
Подставляя x₀ = 5, k = ⁴/₃, y₀ = 7 получим:
y-7 = ⁴/₃(x-5)
или
y = ⁴/₃x + ¹/₃ или 3y -4x — 1 = 0
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
4y + 3x +7 = 0
3y -4x — 1 = 0
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем: x = -1; y = -1
D(-1;-1)
9) Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины:

Найдем расстояние между точкой C(5;7) и прямой AB (4y + 3x +7 = 0)


Длину высоты можно вычислить и по другой формуле, как расстояние между точкой C(5;7) и точкой D(-1;-1).
Расстояние между двумя точками выражается через координаты формулой:

5) уравнение окружности, для которой высота CD есть диаметр;
Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:
(x-a)² + (y-b)² = R²
Так как CD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:


Следовательно, Е(2;3) и R = CD / 2 = 5. Использую формулу, получаем уравнение искомой окружности: (x-2)² + (y-3)² = 25

6) система линейных неравенств, определяющих треугольник АВС.
Уравнение прямой AB: y = ^-3/₄x ^-7/₄
Уравнение прямой AC : y = ¹/₂x + ⁹/₂
Уравнение прямой BC : y = -7x + 42

Система линейных неравенств:
y ≥ ^-3/₄x ^-7/₄ или y + ³/₄x ≥ ^-7/₄ или 3x + 4y ≥ -7
y ≤ ¹/₂x + ⁹/₂ или y — ¹/₂x ≤ ⁹/₂ или — x + 2y ≤ 9
y ≤ -7x + 42 или y + 7x ≤ 42 или 7x + y ≤ 42

Разница между высотой и длиной

13 сентября 2016 г. Автор: Hasa

Ключевое отличие — высота и длина
 

Высота и длина являются важными измерениями, которые используются для определения размера объекта. Высота — это расстояние от основания объекта до его вершины; он измеряет высоту чего-либо. Длина — это измерение самой длинной стороны объекта; он измеряет, как долго что-то. Ключевое отличие между высотой и длиной заключается в том, что высота является вертикальным измерением, тогда как длина является горизонтальным измерением.

Что такое высота?

Высота может быть определена как измерение кого-то или чего-то от головы до ног или от основания до макушки. Это мера вертикального расстояния. Другими словами, высота измеряет, насколько что-то высокое или как высоко оно находится. Он измеряет расстояние от основания до вершины объекта. Рост — это измерение, которое также используется для людей. У людей рост описывает, насколько высок человек.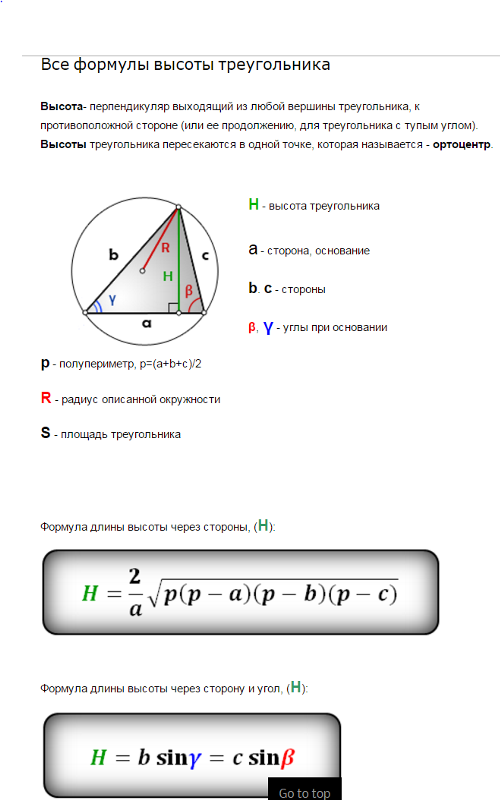 Мы также используем это измерение, чтобы увидеть, насколько высоки деревья, здания и памятники.

Но высота некоторых объектов также может указывать на то, насколько они выше стандартного уровня земли. Например, он может описывать, насколько высока вершина горы от уровня моря, но эту высоту часто называют высотой.

На следующем изображении показана приблизительная высота различных известных статуй.

Будда Весеннего Храма, Статуя Свободы, Родина-мать зовет, Христос-Искупитель, Статуя Давида 

Что такое длина?

Длина – это измерение или протяженность самой длинной стороны объекта. Он описывает длину объекта. В математике термин длина может использоваться для описания размера одномерного, двухмерного или трехмерного объекта. Длина является единственным измерением одномерных объектов. Измерение самой длинной стороны двумерного объекта может быть определено как длина. Короткая сторона известна как ширина или широта. В трехмерных объектах длина — это самая длинная горизонтальная сторона объекта.

Однако, если вы измените положение объекта, эти измерения могут измениться; высота может стать длиной и наоборот. Следующее изображение поможет вам понять разницу между высотой, длиной и шириной.

В чем разница между высотой и длиной?

Определение:

Высота — это измерение чего-либо от основания до вершины.

Длина — это размер или длина самой длинной стороны объекта.

По вертикали и по горизонтали:

Высота измеряет расстояние по вертикали.

Длина измеряет расстояние по горизонтали.

Одномерные объекты:

Высота не является термином, обычно используемым для обозначения измерения одномерных объектов.

Длина — это общий термин, используемый для обозначения измерения одномерных объектов.

Функция:

Высота используется для измерения высоты чего-либо.

Длина используется для измерения длины чего-либо.

Изображение предоставлено:

«Сравнение высоты известных статуй». Анна Фродезиак — собственная работа, CC0) через Commons Wikimedia

; переданы в Commons пользователем: Sreejithk2000 с использованием CommonsHelper. (Общественное достояние) через Commons Wikimedia

Высота и длина | Справочник по физическим измерениям

Фильтр поиска панели навигации Oxford Academic Handbook of Physical MeasurementsClinical GeneticsBooksJournals Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford Academic Handbook of Physical MeasurementsClinical GeneticsBooksJournals Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

CITE

Gripp, Karen W. и др.,

‘Высота и длина’

,

Справочник по физическим измерениям

(

New York,

;

Online EDN,

Oxford Academic

;

Online EDN,

Oxford Academic

;

Online EDN,

Oxford Academic.

, 1 февраля 2014 г.

), https://doi.org/10.1093/med/9780199935710.003.0004,

, по состоянию на 17 декабря 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford Academic Handbook of Physical MeasurementsClinical GeneticsBooksJournals Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford Academic Handbook of Physical MeasurementsClinical GeneticsBooksJournals Термин поиска на микросайте

Advanced Search

Abstract

Длина — это расстояние между макушкой головы и подошвой стопы, когда человек лежит. Это типичный показатель, измеряемый у младенцев. Высота — это расстояние от самой высокой точки головы до подошвы пищевода в срединно-сагиттальной плоскости человека, стоящего в вертикальном положении, измерение, полученное у пожилого человека. Длина и высота изменяются за счет продольного роста. Стандарты были разработаны для международных когорт, этнических когорт и для многих синдромальных состояний.

Ключевые слова: длина тела по возрасту, длина тела по полу, международные стандарты, скорость роста, прогноз роста

Субъект

Клиническая генетика

Отказ от ответственности

Издательство Оксфордского университета не делает заявлений, явных или подразумеваемых, о том, что дозировки лекарств, указанные в этой книге, верны. Поэтому читатели должны всегда… Более Издательство Оксфордского университета не делает заявлений, явных или подразумеваемых, о том, что дозировки лекарств, указанные в этой книге, верны.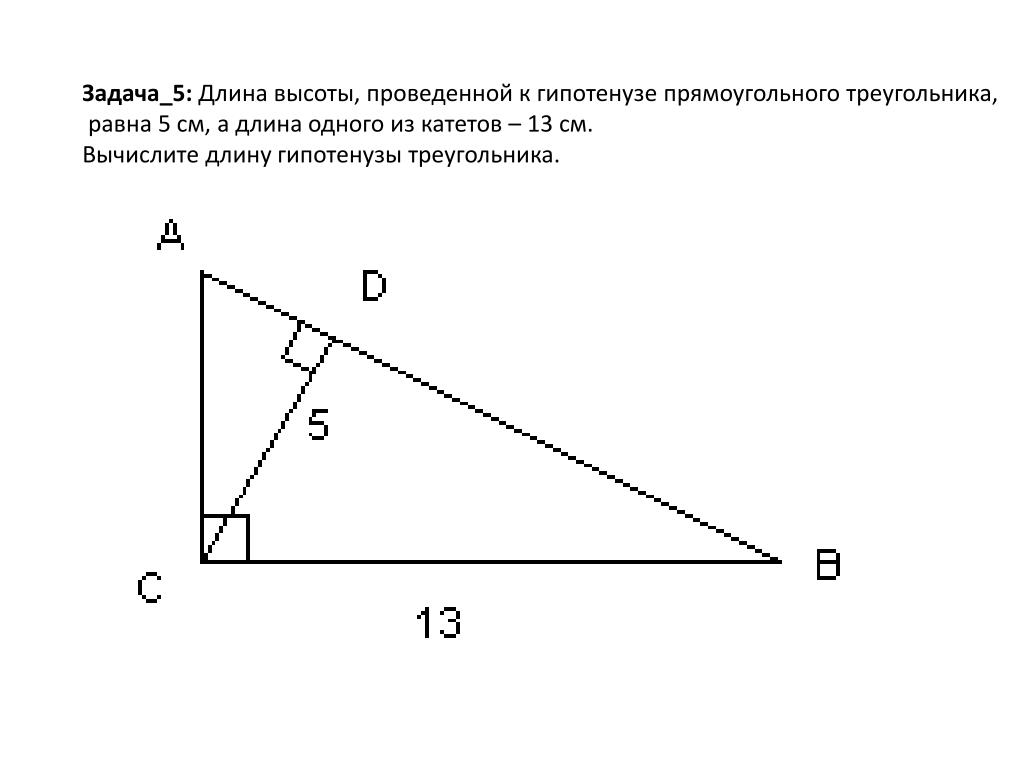 Поэтому читатели должны всегда проверять информацию о продукте и клинических процедурах с самой последней опубликованной информацией о продукте и таблицами данных. предоставленных производителями, а также самые последние кодексы поведения и правила техники безопасности. Авторы и издатели не несут ответственности и юридическую ответственность за любые ошибки в тексте или за неправильное использование или неправильное применение материала в этой работе. Если не указано иное, дозы препаратов и рекомендации для небеременных взрослых, которые не кормят грудью.

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.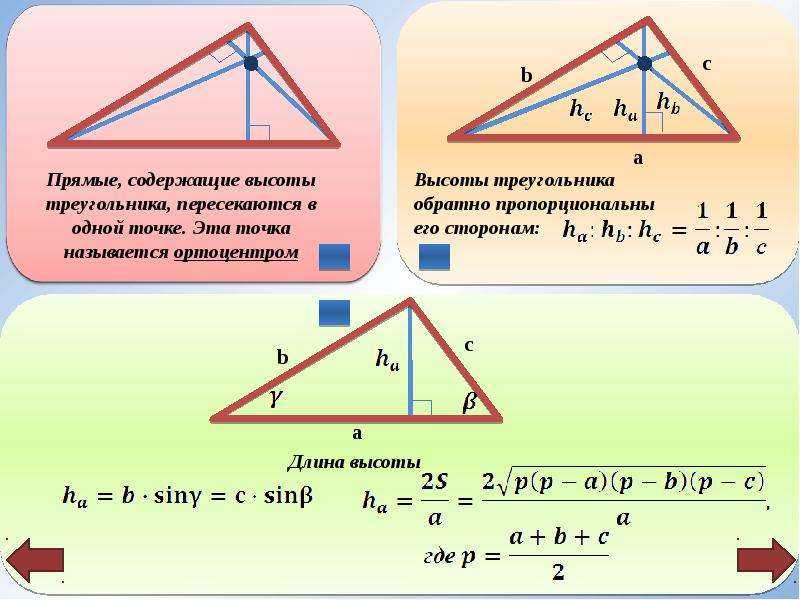 Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа в систему.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.