ГРАДИЕНТ — это… Что такое ГРАДИЕНТ?
— одно из основных понятий векторного анализа и теории нелинейных отображений.
Градиентом скалярной функции 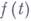 векторного аргумента
векторного аргумента  из евклидова пространства Е n наз. производная функции f(t).по векторному аргументу t, то есть n-мерный вектор с компонентами
из евклидова пространства Е n наз. производная функции f(t).по векторному аргументу t, то есть n-мерный вектор с компонентами  ,
, 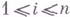 . Существуют следующие обозначения Г. функции f(t) в точке
. Существуют следующие обозначения Г. функции f(t) в точке 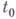 :
:
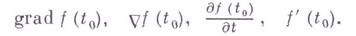
Г. представляет собой ковариантный вектор: компоненты Г., вычисленные в двух различных координатных системах 
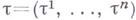 , связаны соотношениями:
, связаны соотношениями: 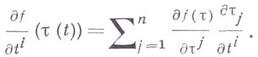
Вектор 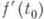 , начало к-рого помещено в точку
, начало к-рого помещено в точку 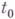 , указывает направление наискорейшего роста функции
, указывает направление наискорейшего роста функции  , ортогональное линии или поверхности уровня функции
, ортогональное линии или поверхности уровня функции 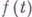 , проходящей через точку
, проходящей через точку  .
.
Производная функции в точке 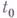
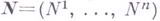 равна проекции Г.
функции на это направление:
равна проекции Г.
функции на это направление: 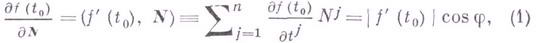
где 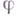 — угол между
— угол между 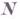 и
и  . Максимум производной достигается при
. Максимум производной достигается при  , т. е. в направлении Г., и равен длине Г.
, т. е. в направлении Г., и равен длине Г.
Понятие Г. тесно связано с понятием дифференциала функции. В случае дифференцируемости 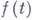 в точке
в точке 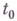
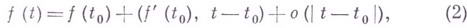
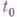
то есть 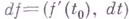 . Существование в точке t0 Г. функции
. Существование в точке t0 Г. функции 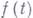 не достаточно для справедливости формулы (2).
не достаточно для справедливости формулы (2).
Точка 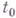 , в к-рой
, в к-рой 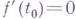 , наз. стационарной (критической или экстремальной) точкой функции
, наз. стационарной (критической или экстремальной) точкой функции 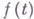 . Такой точкой является, напр., точка локального экстремума функции
. Такой точкой является, напр., точка локального экстремума функции 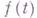
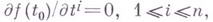 используется для нахождения экстремальной точки t0.
используется для нахождения экстремальной точки t0. При вычислении значения Г. справедливы формулы:
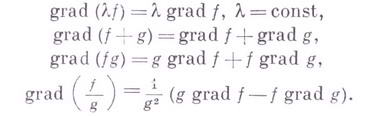
Г. 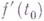 есть производная в точке
есть производная в точке 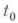 по объему векторной функции объема
по объему векторной функции объема
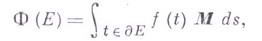
где Е — область с границей  — элемент площади
— элемент площади  , а
, а 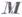
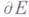 . Другими словами
. Другими словами 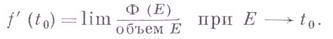
Формулы (1), (2) и перечисленные выше свойства Г. указывают на инвариантный относительно выбора системы координат характер понятия Г.
В криволинейной системе координат 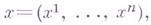 в к-рой квадрат длины элемента
в к-рой квадрат длины элемента
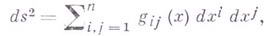
компоненты Г. функции 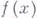 , отнесенного к ортам, касающимся координатных линий в точке х, равны
, отнесенного к ортам, касающимся координатных линий в точке х, равны
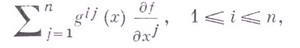
где матрица 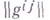
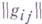 .
. Понятие Г. для более общих векторных функций векторного аргумента вводится при помощи равенства (2), означающего, что Г. есть линейный оператор, действием к-рого на приращение 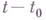 аргумента получается главная линейная часть приращения
аргумента получается главная линейная часть приращения 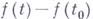 вектор-функции
вектор-функции 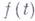 . Напр., если
. Напр., если 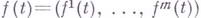 есть m-мерная вектор-функция аргумента
есть m-мерная вектор-функция аргумента  , то ее Г. в течке
, то ее Г. в течке 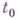
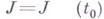 с компонентами
с компонентами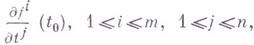
причем
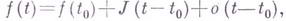
где 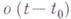 — m-мерный вектор, длина к-рого есть
— m-мерный вектор, длина к-рого есть 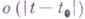 . Матрица
. Матрица 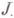 определяется при помощи предельного перехода
определяется при помощи предельного перехода
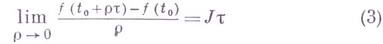
с любым фиксированным n-мерным вектором 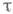 .
.
В бесквнечномерном гильбертовом пространстве определение (3) равносильно определению дифференцируемости по Фреше и Г. при этом совпадает с производной Фреше.
В случае, когда f(t).лежит в бесконечномерном векторном пространстве, возможны различные типы предельного перехода в (3) (см., напр., Гато производная). В теории тензорных полей, заданных в области n-мерного аффинного пространства связности, при помощи Г. описывается главная линейная часть приращения компонент тензора при соответствующем связности параллельном перенесении. Г. тензорного поля

типа (p,q) есть тензор типа (p,q+1) с компонентами
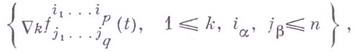
где 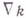 — оператор абсолютного (ковариантного) дифференцирования.
— оператор абсолютного (ковариантного) дифференцирования.
Понятие Г. широко применяется в различных задачах математики, механики и физики. Многие физич. поля могут быть рассматриваемы как градиентные поля (см.
Лит.:[1] Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9 изд., М., 1965: [2] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд , М 1967. л. П. Купцов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Градиент — это… Что такое Градиент?
ГРАДИЕНТ — (от лат. gradiens шагающий) вектор g, показывающий направление наискорейшего изменения данного скалярного поля ? (Р), где Р точка пространства, обозначается g = grad ? (Р). Примеры: градиент температуры, градиент давления, градиент потенциала … Большой Энциклопедический словарь
ГРАДИЕНТ — (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка
ГРАДИЕНТ — [от лат. gradiens (gradientis) шагающий], мера изменения какой либо физической величины в пространстве на единицу длины (расстояния) в том направлении, в котором она убывает наиболее быстро. Понятием градиента широко пользуются в метеорологии,… … Экологический словарь
ГРАДИЕНТ — векторная величина, характеризующая скорость изменения физ. поля по направлению (напр., температурный градиент, вертикальный градиент силы тяжести и т. п.). Г. можно получить расчетным путем (в простейшем случае как разность значений поля в двух… … Геологическая энциклопедия
градиент — Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. [http://www.oceanographers.ru/index.php?option=com… … Справочник технического переводчика
градиент — 1. Изменение значения любой переменной величины, чаще всего используется в метеорологии, например, градиент температуры, барометрический градиент. 2. Крутизна склона, выраженная в градусах, процентах или как отношение … Словарь по географии
градиент — вектор Словарь русских синонимов. градиент сущ., кол во синонимов: 2 • вектор (5) • … Словарь синонимов
градиент — а, м. gradient m., лат. gradiens. Мера возрастания или убывания в пространстве какой л. физической величины при перемещении на единицу длины. БАС 2. Лекс. Брокг.: градиент; Уш. 1935: градие/нт; БСЭ 2: градие/нтный ветер; БСЭ 3: градиентоме/тр,… … Исторический словарь галлицизмов русского языка
ГРАДИЕНТ — ГРАДИЕНТ, в метеорологии и геофизике быстрота изменения некоторого элемента (температуры, давления, электрич. поля) в направлении, перпендикулярном к поверхностям уровня (т. е. поверхностям равных температур, равных давлений и пр.). Градиент… … Большая медицинская энциклопедия
градиент — закономерное количественное изменение, отражающее убывание или возрастание некоего свойства или показателя, например, градиент раздражителя (см. таксис). Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия
ГРАДИЕНТ — ГРАДИЕНТ, градиента, муж. (от лат. gradiens восходящий) (научн.). Изменение какой нибудь величины на какую нибудь единицу длины. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Значение слова «Градиент» в 10 онлайн словарях Даль, Ожегов, Ефремова и др.
Поделиться значением слова:Ударение: градие́нт м.
- Мера возрастания или убывания в пространстве какой-л. физической величины при перемещении на единицу длины.
ГРАДИЕ́НТ, градиента, ·муж. (от ·лат. gradiens — восходящий) (научн.). Изменение какой-нибудь величины на какую-нибудь единицу длины.
вектор
(от лат. gradiens — шагающий), вектор g, показывающий направление наискорейшего изменения данного скалярного поля ? (Р), где Р — точка пространства, обозначается g = grad ? (Р). Примеры: градиент температуры, градиент давления, градиент потенциала.
(лат. gradiens, gradientis шагающий, движущийся) в биологии величина, отражающая количественное изменение каких-либо морфологических или функциональных (в т. ч. физико-химических) свойств вдоль одной из осей тела, органа или клетки.
вектор, микроградиент
градие́нт,
градие́нты,
градие́нта,
градие́нтов,
градие́нту,
градие́нтам,
градие́нт,
градие́нты,
градие́нтом,
градие́нтами,
градие́нте,
градие́нтах
{иэ}, а, м.
1. мат. Вектор, показывающий направление наискорейшего возрастания некоторой функции.
2. физ. Мера возрастания или убывания в пространстве какой-нибудь физической величины на единицу длины. Градиентный — относящийся к градиенту, градиентам. Геотермический градиент (геол.) — ве-личина повышения температуры Земли с углублением на единицу длины. Горизонтальный бариче-ский градиент (физ.) — изменение давления на единицу расстояния по нормали к изобарической по-верхности или изобаре. Вертикальный градиент температуры (метеор.) — изменение температуры в атмосфере с высотой.

Градиент — это… Что такое Градиент?
ГРАДИЕНТ — (от лат. gradiens шагающий) вектор g, показывающий направление наискорейшего изменения данного скалярного поля ? (Р), где Р точка пространства, обозначается g = grad ? (Р). Примеры: градиент температуры, градиент давления, градиент потенциала … Большой Энциклопедический словарь
ГРАДИЕНТ — (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка
ГРАДИЕНТ — [от лат. gradiens (gradientis) шагающий], мера изменения какой либо физической величины в пространстве на единицу длины (расстояния) в том направлении, в котором она убывает наиболее быстро. Понятием градиента широко пользуются в метеорологии,… … Экологический словарь
ГРАДИЕНТ — векторная величина, характеризующая скорость изменения физ. поля по направлению (напр., температурный градиент, вертикальный градиент силы тяжести и т. п.). Г. можно получить расчетным путем (в простейшем случае как разность значений поля в двух… … Геологическая энциклопедия
градиент — Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. [http://www.oceanographers.ru/index.php?option=com… … Справочник технического переводчика
градиент — 1. Изменение значения любой переменной величины, чаще всего используется в метеорологии, например, градиент температуры, барометрический градиент. 2. Крутизна склона, выраженная в градусах, процентах или как отношение … Словарь по географии
градиент — вектор Словарь русских синонимов. градиент сущ., кол во синонимов: 2 • вектор (5) • … Словарь синонимов
градиент — а, м. gradient m., лат. gradiens. Мера возрастания или убывания в пространстве какой л. физической величины при перемещении на единицу длины. БАС 2. Лекс. Брокг.: градиент; Уш. 1935: градие/нт; БСЭ 2: градие/нтный ветер; БСЭ 3: градиентоме/тр,… … Исторический словарь галлицизмов русского языка
ГРАДИЕНТ — ГРАДИЕНТ, в метеорологии и геофизике быстрота изменения некоторого элемента (температуры, давления, электрич. поля) в направлении, перпендикулярном к поверхностям уровня (т. е. поверхностям равных температур, равных давлений и пр.). Градиент… … Большая медицинская энциклопедия
градиент — закономерное количественное изменение, отражающее убывание или возрастание некоего свойства или показателя, например, градиент раздражителя (см. таксис). Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия
ГРАДИЕНТ — ГРАДИЕНТ, градиента, муж. (от лат. gradiens восходящий) (научн.). Изменение какой нибудь величины на какую нибудь единицу длины. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Градиент | Математика | Fandom
Файл:Градиент холма.gifГрадиент (от , род. падеж gradientis — шагающий болт ) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.
Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами $ \frac {\partial \phi} {\partial x} $, $ \frac {\partial \phi} {\partial y} $, $ \frac {\partial \phi} {\partial z} $, где φ — некоторая скалярная функция координат x, y, z.
Если $ \phi $ — функция n переменных $ x_1,\ldots,x_n $, то её градиентом будет n-мерный вектор
- $ \left(\frac{\partial \phi}{\partial x_1},\ldots,\frac{\partial \phi}{\partial x_n}\right) $,
компоненты которого равны частным производным $ \phi $ по всем её аргументам.
Градиент обозначается $ \mathrm{grad}\phi $ или, с использованием оператора набла, $ \nabla \phi $.
Из определения градиента следует, что:
$ \mathrm{grad}\phi = \nabla \phi = \frac {\partial \phi} {\partial x} \vec e_x + \frac {\partial \phi} {\partial y} \vec e_y + \frac {\partial \phi} {\partial z} \vec e_z $
Свойства
Для любого постоянного числа $ c\in\R $ и скалярных полей $ \vec{u}, \vec{v}:\R^n\to\R $ справедливо следующее:
- $ \operatorname{grad}\,c=\vec{0} $
Линейность
- $ \operatorname{grad}\,(c\cdot \vec{u})=c\cdot\operatorname{grad}\,\vec{u} $
- $ \operatorname{grad}\,(\vec{u}+\vec{v})=\operatorname{grad}\,\vec{u}+\operatorname{grad}\,\vec{v} $
Правило Лейбница
- $ \operatorname{grad}\,(\vec{u}\cdot \vec{v}) = \vec{u}\cdot\operatorname{grad}\,\vec{v} + \vec{v}\cdot\operatorname{grad}\,\vec{u} $, где $ \vec{u}\cdot\vec{v} $ — скалярное произведение векторов $ \vec u $ и $ \vec v $.
Пример
Например, градиент функции $ \phi(x,y,z)=2x+3y^2-sin(z) $ будет представлять собой:
- $ \nabla \phi = \begin{pmatrix} {\frac{\partial \phi}{\partial x}}, {\frac{\partial \phi}{\partial y}}, {\frac{\partial \phi}{\partial z}} \end{pmatrix} = \begin{pmatrix} {2,} { 6y,} { -cos(z)} \end{pmatrix} $
В физике
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по направлению температуры среды и т.д.. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
Связь с производной по направлению
Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции $ \phi $ по направлению $ \vec{e}=(e_1,\ldots,e_n) $ равняется скалярному произведению градиента $ \phi $ на единичный вектор $ \vec{e} $:
- $ \frac{\partial \phi}{\partial \vec e}=\frac{\partial \phi}{\partial x_1} e_1+\cdots+\frac{\partial \phi}{\partial x_n} e_n = (\nabla\!\phi,\vec e) $
Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть набор всех её частных производных.
Градиент в ортогональных криволинейных координатах
- $ \operatorname{grad} U(q_1, q_2, q_3) = \frac{1}{H_1}\frac{\partial U}{\partial q_1}\vec i + \frac{1}{H_2}\frac{\partial U}{\partial q_2}\vec j + \frac{1}{H_3}\frac{\partial U}{\partial q_3}\vec k $,
где Hi — коэффициенты Ламе.
Цилиндрические координаты
Коэффициенты Ламе:
- $ \begin{matrix}H_1 = 1 \\ H_2 = r \\ H_3 = 1 \end{matrix} $.
Отсюда:
- $ \operatorname{grad} U(r, \theta, z) = \frac{\partial U}{\partial r}\vec r + \frac{1}{r}\frac{\partial U}{\partial \theta}\vec \theta + \frac{\partial U}{\partial z}\vec z $.
Сферические координаты
Коэффициенты Ламе:
- $ \begin{matrix}H_1 = 1 \\ H_2 = r \\ H_3 = r\sin{\theta} \end{matrix} $.
Отсюда:
- $ \operatorname{grad} U(r, \theta, \phi) = \frac{\partial U}{\partial r}\vec r + \frac{1}{r}\frac{\partial U}{\partial \phi}\vec \phi + \frac{1}{r\sin{\theta}}\frac{\partial U}{\partial\theta }\vec \theta $.
См. также
cs:Gradienthe:גרדיאנטnl:Gradiënt pl:Gradient (matematyka)sl:Gradient sv:Gradient uk:Градієнт
Градиент (компьютерная графика) — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 июля 2018; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 июля 2018; проверки требует 1 правка. Эта статья о виде заливки в компьютерной графике; о векторе см. Градиент. Логотип, созданный с применением градиента.
Логотип, созданный с применением градиента.Градие́нт (англ. Gradient) — вид заливки в компьютерной графике, которая по заданным параметрам цвета в ключевых точках рассчитывает промежуточные цвета остальных точек. При этом создаются плавные переходы из одного цвета в другой. Обычно в градиенте можно использовать более двух цветов и дополнительно указывать настройки прозрачности и смещения границы цветов.
Кроме того, для удобства обозначения, градиентом часто называют сами цвета отправных точек, относительно которых происходит расчет заливки. При этом слово градиент имеет смысловую окраску «максимальная градация цвета» или «максимальный уклон, отклонение» достигнутое цветом в этой точке.
Основные виды градиентов:
- Линейный — ключевые точки располагаются на одной прямой.
- Круговой — относительно первой ключевой точки строятся концентрические окружности, цвет которых зависит от расположения остальных ключевых точек.
- Угловой (конусный) — ключевые точки располагаются по кругу.
- Отражённый — похож на линейный, составляется из двух частей: линейного градиента и его воображаемого отражения в зеркале.
- Ромбовидный (алмазный) — напоминает собой алмаз.
Градиенты используются как в растровой, так и в векторной графике. Широкое применение они нашли в дизайне (в частности, в веб-дизайне).
Что такое градиент
Содержание статьи:
Определение понятия
Градиент – это одно из часто использующихся понятий, которое может обозначать очень много разнообразных вещей. Оно используется в разнообразных науках и направлениях деятельности. Именно поэтому очень важно понимать все его значения, чтобы корректно употреблять данное слово в своей речи.
Градиент в переводе с латыни означает «тот, который идет, растет». В словарях обозначение этого понятие дано совершенно различное. В настоящее время можно найти следующие определения данного термина:
- вектор, что указывает направление роста той или иной величины;
- увеличение или уменьшение показателя на единицу и др.
Градиент может обозначать, как количественные изменения каких-либо величин, так и качественные. Используется данное понятие в математике, физике, метеорологии, географии, медицине, экономике, дизайне, маникюрном деле и рукоделии.
Математика
В математических науках под градиентом специалисты подразумевают вектор, который указывает направление увеличения функции в скалярном поле от одного показателя к другому. Для того чтобы рассчитать его величину, используются нахождения значений отдельных производных.
С целью определения наиболее быстрого изменения исследуемой функции, математики выбирают на имеющемся графике 2 точки. После этого обозначается начально и конечное положение вектора. В данной ситуации скоростью роста значения считается собственно сам размер градиента.
Физика
В различных областях физики градиент может обозначать разнообразные понятия. Такой термин используется при описании оптических явлений, скорости, давления и температурных изменений. В каждом из этих случаев под градиентом подразумевается увеличение или уменьшение какого-либо показателя на одну единицу.
Отдельно стоит выделить такое понятие, как градиент потенциала. Последний используется для определения скорости изменения величины по отношению к силовой линии. Осуществляется данное действие при помощи вычисления при наличии известного напряжения посредством вектора напряженности.
География
Впервые термин градиент использовали метеорологи. Под ним подразумевалось направление изменения какой-либо величины или показателей. Это касалось прежде всего температуры, атмосферного давления и значений ветрового воздействия.
Лишь через определенный период времени градиент начали использовать в математике. Первым это сделал Максвелл.
В зависимости от анализируемых климатических условий, градиент в метеорологии может быть, как горизонтальным, так и вертикальным.
Отдельно стоит отметить, что градиентом могут обозначать величину или же угол уклону. Для этого высоту определенного участка делят на продолжительность его проекции на плоскость, выражая полученное число в процентах.
Медицина
В медицине существует несколько терминов, связанным со словом «градиент», таких как:
- Градиент температурный. Он характеризует разницу в аналогичных показателях внутренних систем и кожных покровов тела.
- Градиент физиологический. Он обозначает те или иные изменения в какой-либо системе органов или же организме в целом.
- Градиент метаболический. Под ним подразумевается интенсивность обменных процессов.
- Градиент давления. Он используется для обозначения разницы артериального давления в двух связанных друг с другом частях сердца.
- Убывающий градиент автоматии. Это понятие характеризует автоматическое снижение частотности возбуждения сердечной мышцы.
- Амплитуда градиента пульса. Данный показатель применяется для обозначения поражения сосуда и определения его степени посредством анализа разницы амплитуд систолических волн на кардиограмме.
Таким образом, понятие градиента в медицине может иметь массу разнообразных отличающихся друг от друга значений.
Экономика
В экономике термин градиент обрел не очень значительное распространение. Его используется преимущественно в тех случаях, когда специалисты определяют функцию полезности.
Она предполагает возможность представить предпочтения какого-либо ограниченного круга потребителей при наличии нескольких альтернативных вариантов выбора.
Градиент характеризует в экономике найденные оптимальные для конкретной группы человек потребительские наборы.
Дизайн
В дизайне под градиентом подразумевается не количественное, а качественное изменения показателя цвета. Это понятие используют для обозначения плавного и продолжительного перехода определенного оттенка в иной.
Существуют следующие примеры градиентов в дизайне:
- В стиле омбре часто используется переход более светлого цвета в темный или же тусклый.
- В линзах очков нередко используется специальная технология производства линзы, когда ее низ практически прозрачный, а верх – полностью окрашен в темный цвет.
Отдельно стоит отметить, что в программах для веб-дизайна существует функция градиента для создания большого количества различных эффектов. Такая опция присутствует в Photoshop, CorelDraw, Paint и т.д. Эффект, который создает градиент, напрямую зависит от его типа.
Сфера красоты
В салонах красоты мастера под градиентом подразумевают цветовые переходы. Чаще всего речь идет о покраске волосы или же маникюре.
Техника, которая характеризует постепенный переход светлого цвета в темный, называется омбре.
В салонах можно сделать, как горизонтальный, так и вертикальный градиент волос. К тому же существует возможность заказать смену цвета с переходом.
Рукоделие
В рукоделии градиентом именуют несколько различных техник, таких как:
- Создание предметов в стиле декупаж с нанесением на них узора посредством трафарета, имея при этом в качестве фона градиент цвета.
- Пошив и проектирование одежды, на которое отображается постепенный переход определенного оттенка в другой.
Таким образом, можно сделать вывод о том, что градиент – это очень многозначный термин, который использоваться может в самых разнообразных сферах – от науки для рукоделия. Именно поэтому использовать данное понятие необходимо только лишь с четким пониманием его значения.





