высота, ширина, длина. Ширина — Мир Окон 🏠
Содержание
Обозначение: высота, ширина, длина. Ширина
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.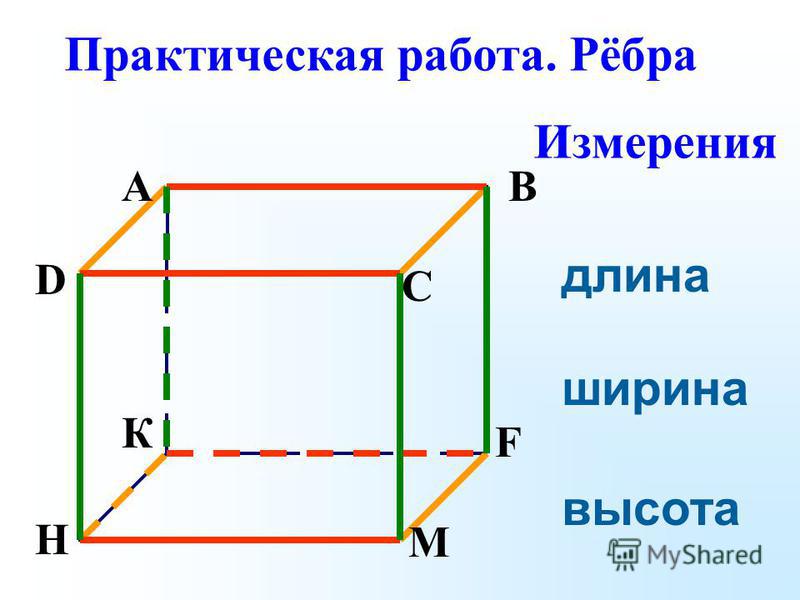
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.
Высота ширина длина — латинские обозначения: как правильно пишутся размеры и чем отличаются величины
Решая геометрические задачи, ученики сталкиваются с вопросом: как правильно обозначить те или иные части чертежа? Например, высоту треугольника, ширину прямоугольника, размеры бассейна. Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила.
Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила.
Как обозначаются различные параметры
В единой системе измерения используется обозначение латинскими буквами:
- длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А;
- высоту или глубину – h;
- ширину – В.
Что такое система СИ, ученики узнают лишь в средней школе, поэтому обычно в младших классах специального обозначениям для этих величин не вводят.
Как обозначить глубину?
Почему же для высоты и глубины применяется одна и та же буква? Если вы построите чертеж параллелепипеда, то здесь вы отметите высоту фигуры.
А если составить чертеж прямоугольного бассейна того же размера, что и параллелепипед, то обозначается глубина. Таким образом, можно сказать, высота и глубина в этом случае будут одной величиной.
Таким образом, можно сказать, высота и глубина в этом случае будут одной величиной.
[warning]Внимание! Высота и глубина – две величины, которые обозначают один и тот же перпендикуляр, соединяющий две противоположные плоскости.[/warning]
Понятие «глубина» встречается и в географии. На картах она отображается цветом. Если речь идет о водных просторах, то чем темнее синий, цвет, тем больше глубина, а если речь идет о суше, то низменности обозначаются темно-зеленым цветом.
В черчении эта величина обозначается литерой S. Она позволяет создать полное восприятие объекта иногда даже с одним видом.
Что бывает длинным
Что же такое длина и как обозначается этот показатель? Она указывает расстояние от точки до точки, то есть размер отрезка. В геометрических задачах его принято обозначать как А. В стереометрии ее могут обозначать и А, и l (например, в задачах, где встречается прямая, пересекающая плоскость).
В физике же длина маятника, плеча рычага и т. д. в «Дано» обозначается буквой l, так как речь идет об отдельной прямой.
д. в «Дано» обозначается буквой l, так как речь идет об отдельной прямой.
Отличие длины от высоты
Длина – это величина, которая характеризует протяженность линии.
А высота – это перпендикуляр, опущенный на противолежащую плоскость.
То есть можно сделать вывод, что длина от высоты отличается тем, что является частью фигуры, совпадая с ее гранью, а высота получается в результате дополнительного построения на чертеже.
Высоту проводят для того, чтобы получить новые данные для решения задач, а также новых фигур в составе исходной.
Вот такой ширины
Ширина предмета необходима для того, чтобы понять форму как двумерного, так и трехмерного объекта. Как правило, она обозначается буквой В.
Измеряется ширина в метрах (по СИ). Но если предмет слишком мал, то для удобства используют более мелкие единицы измерения:
- дециметры,
- сантиметры,
- миллиметры,
- микрометры и т.
 д.
д.
А если предмет слишком крупный, то пишутся такие приставки:
- Кило- (10³),
- Мега- (106),
- Гига- (109),
- Тера- (1012) и т.д.
Разумеется, такие крупные единицы измерения необходимы, например, для астрономии. Также они применяются в квантовой физике, микробиологии и так далее.
В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.
Это значит, что стороны, образующие углы различны.
Как правило, более длинную сторону прямоугольника называют длиной, а ширина прямоугольника — это его короткая сторона.
[stop]Важно! Зная такие данные, как длина и ширина прямоугольника, можно найти его периметр, площадь, длину диагоналей и угол между ними. Вокруг прямоугольника всегда можно описать окружность. Эти свойства работают и в обратном направлении. [/stop]
В чем измеряются размеры длины, ширины и высоты по СИ
По единой системе измерения длина, высота и ширина измеряются в метрах. Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.
Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.
Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать
значения приставок.- Дека — 101,
- Гекто — 102,
- Кило — 103,
- Мега — 106,
- Гига — 109,
- Деци – 10-1,
- Санти – 10-2,
- Милли – 10-3,
- Микро — 10-6,
- Нано – 10-9.
После подсчетов эти единицы должны быть переведены в метры.
Существуют также внесистемные единицы, но они встречаются очень редко:
- миля – 1,6 км;
- фут – 12 дюймов – 0,3048 м;
- ярд – 36 дюймов – 91,44 мм;
- дюйм – 25,4 мм и т. д.
При решении задач такие единицы должны быть переведены в метры.
При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы
(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).
А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.
Обозначения длины, ширины, высоты в геометрии
Измеряем геометрические параметры
Вывод
Теперь вы знаете, какой буквой обозначается длина, в чем измеряется ширина прямоугольника, и сможете сами объяснить любому, как обозначаются различные параметры.
Это интересно! Легкие правила округления чисел после запятой
геометрия — Найдите идеальную ширину и высоту n одинаковых прямоугольников внутри прямоугольника
спросил
Изменено
2 года, 8 месяцев назад
Просмотрено
132 раза
$\begingroup$
У меня есть прямоугольник, его ширина a и его высота b
Я хочу покрыть максимальную поверхность этого прямоугольника n прямоугольников, эти прямоугольники должны иметь одинаковые размеры и соблюдать соотношение w к h
как можно Я вычисляю размеры n прямоугольников?
Я пробовал следующее
$$c = \sqrt{a*b* w/h \over n}$$
$$width = c * w$$
$$height = c * h$$
Но это не совсем работает, потому что это ищет покрытие всего прямоугольника (поэтому в некоторых случаях результирующие размеры делают прямоугольник больше, чем прямоугольник ab
- геометрия
- площадь
- поверхности
- соотношение
$\endgroup$
$\begingroup$
Если на Рис. 1 не показан пример того, что вы ожидаете, не читайте дальше, так как приведенное ниже описание основано на нем.
1 не показан пример того, что вы ожидаете, не читайте дальше, так как приведенное ниже описание основано на нем.
Предполагается, что заданы $a$, $b$, $h$, $w$ и $n$. Пусть высота маленьких прямоугольников равна $k$. Тогда ширина маленьких прямоугольников равна $k\frac{w}{h}$. Теперь мы можем узнать, сколько маленьких прямоугольников нам нужно, чтобы покрыть большой прямоугольник, как показано ниже
$$\mathrm{Nr.\space of\space small\space прямоугольники\space on\space a\space column} =n_c= \Big\lfloor \frac{b}{k}\Big\rfloor \le \ frac{b}{k}\qquad\quad\space$$
$$\mathrm{Nr.\space of\space small\space прямоугольники\space on\space a\space row} = n_r=\Big\lfloor \frac{a}{k} \times \frac{h}{w}\Big\rfloor \le \frac{a}{k} \times \frac{h}{w}$$
$$\следовательно \quad n = n_c\times n_r = \Big\lfloor \frac{b}{k}\Big\rfloor \times \Big\lfloor \frac{a}{k} \times \frac{h}{w}\ Большой\rэтаж \le \frac{a}{k}\times \frac{b}{k}\times \frac{h}{w}.$$
Как видите, связь между $n$ и неизвестным $k$ была получена с помощью функций пола.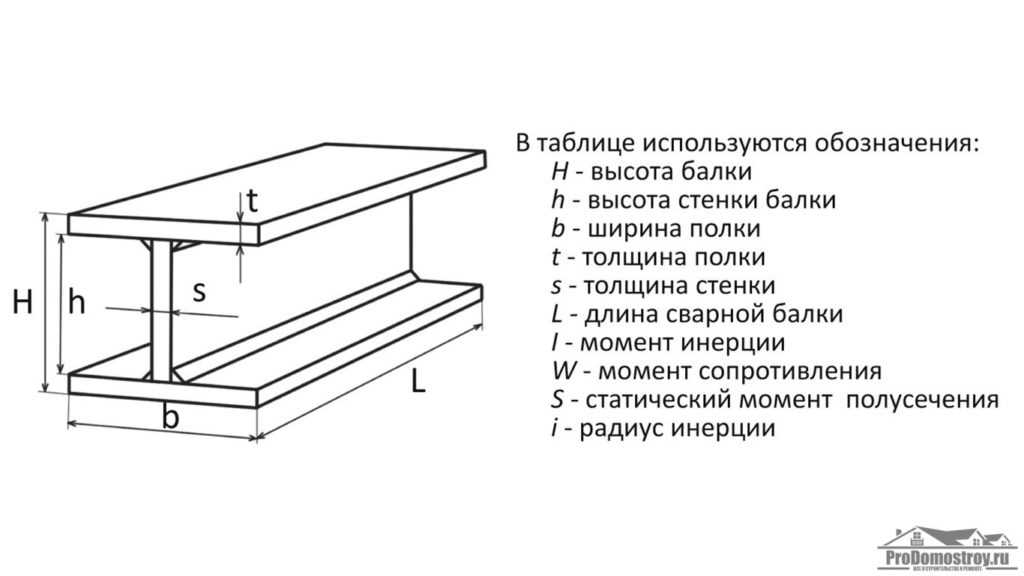 Эти функции не позволяют нам сделать $k$ предметом уравнения, которое нам нужно для определения высоты и ширины маленьких прямоугольников. Поэтому я думаю, что ваш вопрос не может быть решен математически. Однако можно найти решение экспериментальным путем.
Эти функции не позволяют нам сделать $k$ предметом уравнения, которое нам нужно для определения высоты и ширины маленьких прямоугольников. Поэтому я думаю, что ваш вопрос не может быть решен математически. Однако можно найти решение экспериментальным путем.
$\endgroup$
6
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
геометрия — высота/ширина обрезанного круга с учетом радиуса и углов, лежащих в центре
Просто подумайте о терминах расстояния. Вам нужно найти размер наименьшего прямоугольника, который мог бы содержать ваш обрезанный диск.
Вы берете два угла $\theta_1$ и $\theta_2$. Я предполагаю, что:
$$180° \geq \theta_1 \geq \theta_2 \geq -180°$$
Вычислим $h = y_{\mathrm{max}}-y_{\mathrm{min}}$ и $w=x_{\mathrm{max}}-x_{\mathrm{min}}$, поэтому у вас есть разные возможности:
$\bullet $, если $\theta_1\geq 0 \geq \theta_2$, то $x_{ \mathrm{max}} = r$ и $x_{\mathrm{min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\})$
$\bullet $ если $0>\theta_1 \geq \theta_2$, то $x_{\mathrm{max}} = \mathrm{max}(r \cos \theta_1, 0)$ и $x_{\mathrm{min}} = \mathrm {мин}(\{0,r \cos \theta_1,r \cos \theta_2\})$
$\bullet $ если $\theta_1 \geq \theta_2>0$, то $x_{\mathrm{max}} = \mathrm{max}(r \cos \theta_2, 0)$ и $x_{\mathrm{ min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\})$
Мы можем суммировать это как:
$x_{\mathrm{min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) $
Если $\theta_1 \theta_2 \geq 0$, то $x_{\mathrm{max}} = \mathrm {max}(\{0,r \cos \theta_1,r \cos \theta_2\})$ else $x_{\mathrm{max}} = r$
Следовательно:
$$ \boxed{w= \ влево \ {\ {начать массив} {ll}
\mathrm{max}(\{0,r \cos \theta_1,r \cos \theta_2\})-\mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) \ ; \mathrm{если} \; \theta_1 \theta_2 \geq 0 \\
r-\mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) \text{иначе} \\
\end{массив} \right.
Стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм «ЕвроЭксперт»
Главная \ Каталог \Лабораторная мебель «Эксперт» \Лабораторная мебель серии «ЕвроЭксперт» \ Островные столы «ЕвроЭксперт» \ Стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм «ЕвроЭксперт»
Особенности
- в основе стола – прочный металлический каркас с порошковым покрытием, обеспечивающий надежность конструкции;
- лицевой съемный экран для быстрого доступа к коммуникациям;
- допустимая распределенная нагрузка на рабочую поверхность до 500 кг;
- регулируемые опоры для компенсации неровностей пола.
| Характеристики | Значения | |||||
|---|---|---|---|---|---|---|
| Серия | ЕвроЭксперт | |||||
| Артикул | 21-15 | |||||
| Габаритные размеры, мм: | ||||||
| длина | 1200 | |||||
| глубина | 1500 | |||||
| высота | 900 | |||||
| Цвет/Текстура | Светло-серый, серый/ матовая в два цвета | |||||
| Материал | Металл | |||||
| Рабочая поверхность: | ламинат высокого давления | |||||
| керамогранит | ||||||
| дюркон | ||||||
| дюркон с бортиком | ||||||
| лабгрейд | ||||||
| искусственный кварцевый камень | ||||||
| бесшовный керамогранит | ||||||
| Комплектация: | открытый | |||||
| для работы стоя | ||||||
| для работы сидя | ||||||
| Дополнительно: | подвесная или мобильная тумба | |||||
|
установка сервисной или титровальной надстройки |
||||||
| установка электрического блока с розетками | ||||||
|
подвод/слив воды, подвод газовых коммуникаций |
||||||
| установка выдвижной полки для клавиатуры | ||||||
Купить стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм “ЕвроЭксперт”
Торговый дом «Лабор» уже много лет работает в сфере производства специализированной мебели для оснащения лабораторий. Мы реализуем прочные и практичные столы лабораторные островные для оптимизации пространства в помещении. Функциональные модели помогут организовать рабочий процесс даже в небольшой комнате.
Мы реализуем прочные и практичные столы лабораторные островные для оптимизации пространства в помещении. Функциональные модели помогут организовать рабочий процесс даже в небольшой комнате.
Работа в лаборатории трудная и выматывающая, ведь многие процессы приходится выполнять стоя. Чтобы обеспечить нормальные условия и повысить работоспособность, необходимо приобрести функциональную мебель. Мы предлагаем стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм. Благодаря высоте 90 см, за ним комфортно работать сидя или стоя.
В зависимости от предназначения, выбирается материал столешницы. Наша компания предлагает разные варианты для оснащения лабораторий любого типа.
Порочная, надежная конструкция выдержит любые испытания. В основе — металлический каркас. Поверхность покрыта специальной порошковой краской — эпоксидной. Чтобы обеспечить доступ к оборудованию, стол оснащен открывающимися экранами.
Стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм предназначен для продуктивной работы. Полки и ящики входят в комплектацию. В них можно хранить все необходимые материалы для лаборатории.
Полки и ящики входят в комплектацию. В них можно хранить все необходимые материалы для лаборатории.
Предлагаемая продукция отмечена сертификатами европейского образца ISO 9001:2015, поэтому может использоваться для любых работ, что подтверждается наличием сертификата по ГОСТ 16371-2014. Торговый дом «Лабор» предлагает проектирование, замер и изготовление мебели по индивидуальным параметрам. Доставка, монтаж и гарантийное обслуживание проводят наши мастера.
Закажите стол лабораторный островной длиной L=1200 мм, высотой H=900 мм, глубиной B=1500 мм в Торговом доме «Лабор» с доставкой!
ВАМ НЕОБХОДИМА ПОМОЩЬ В ПОДБОРЕ МЕБЕЛИ?
Позвоните нам или оставьте свой номер для звонка менеджера
8 (812) 509-60-85
Согласен на обработку персональных данных
Рекомендуем посмотреть
Надстройка лабораторная сервисная высотой H=900-1000 мм «ЕвроЭксперт»
Стол лабораторный островной длиной L=900 мм, высотой H=750 мм, глубиной B=1500 мм «ЕвроЭксперт»
Стол лабораторный островной высотой H=750-900 мм
Стол лабораторный островной длиной L=1800 мм, высотой H=900 мм, глубиной B=1500 мм «ЕвроЭксперт»
Стол лабораторный островной длиной L=1800 мм, высотой H=750 мм, глубиной B=1500 мм «ЕвроЭксперт»
Надстройка лабораторная титровальная высотой H=900-1000 мм «ЕвроЭксперт»
Калькулятор объема кубоида
Создано Adena Benn
Отзыв от Krishna Nelaturu
Последнее обновление: 02 ноября 2022 г.
- Определение прямоугольного параллелепипеда
- Как используйте наш калькулятор объема прямоугольного параллелепипеда
- Как найти объем прямоугольного параллелепипеда
- Подобные калькуляторы
- Часто задаваемые вопросы
У вас проблемы с математикой и вам нужна помощь расчет объема прямоугольного параллелепипеда ? Вы знаете объем, но нужна помощь нахождение измерения одного из ребер ? Вы пришли в нужное место. Наш калькулятор объема прямоугольного параллелепипеда прост в использовании и содержит много информации, которая поможет вам в математике.
В этой статье рассматриваются:
- Определение прямоугольного параллелепипеда;
- Объем формулы прямоугольного параллелепипеда;
- Как рассчитать объем прямоугольного параллелепипеда;
- Количество вершин и ребер прямоугольного параллелепипеда; и более.
Определение прямоугольного параллелепипеда
Прямоугольный параллелепипед — это трехмерная фигура, имеющая много общего с обычной коробкой 📦. Он имеет шести прямоугольных поверхностей. Его высота, ширина и длина имеют разные размеры.
Он имеет шести прямоугольных поверхностей. Его высота, ширина и длина имеют разные размеры.
🙋 Задумывались ли вы когда-нибудь сколько ребер у прямоугольного параллелепипеда ? Кубоид имеет двенадцать ребер, шесть граней и восемь вершин.
Как использовать наш калькулятор объема прямоугольного параллелепипеда
Чтобы использовать наш калькулятор объема параллелепипеда , вам просто нужно ввести длину, ширину и высоту данного прямоугольного параллелепипеда, и объем будет рассчитан для вас в режиме реального времени.
Кроме того, вы также можете ввести два из этих измерений (скажем, длину и высоту) вместе с объемом, и наш калькулятор вычислит измерение для неизвестной стороны .
В качестве бонуса наш калькулятор также дает вам диагональ прямоугольного параллелепипеда.
Как найти объем прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда , вам сначала нужно знать длину ( l ), ширину ( w ) и высоту ( h ) кубоид. 3
\end{выравнивание*}громкость=8×9×7 см=504 см3
3
\end{выравнивание*}громкость=8×9×7 см=504 см3
Похожие калькуляторы
Вас интересуют аналогичные калькуляторы? Ознакомьтесь с инструментами ниже:
- Калькулятор прямоугольной призмы;
- Площадь кубовидной поверхности; и
- Прямоугольный калькулятор.
Часто задаваемые вопросы
Как найти объем прямоугольного параллелепипеда, используя его длину, высоту и ширину?
Чтобы найти объем прямоугольного параллелепипеда по его длине, высоте и ширине , нам нужно:
- Получить формулу для вычисления объема параллелепипеда:
объем = д × ш × в - Подставьте значения длины, ширины и высоты, скажем, 5, 4 и 6 соответственно.
объем = 5 × 4 × 6 - Рассчитать объем:
объем = 120
Как найти высоту прямоугольного параллелепипеда по длине, ширине и объему?
Предположим, что длина, ширина и объем прямоугольного параллелепипеда равны 9, 8 и 360 дюймов соответственно.
Используя формулу объема прямоугольного параллелепипеда:
объем = л × ш × в кубических единицСделайте h предметом формулы:
h = объем/(l × w) кубических единицПодставить данные значения:
h = 360/(9 × 8) в 3Решите уравнение:
h = 6 in 3
Адена Бенн
Длина (л)
Ширина (ш)
Высота (в)
Объем
Диагональ (d)
Посмотреть 23 похожих калькулятора 3d геометрии 📦
Площадь полушарияCubeCube Calc: найти v, a, d… еще 20
Калькулятор площади поверхности
Используйте калькуляторы ниже для расчета площади поверхности из несколько распространенных форм.
Площадь поверхности шара
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь поверхности прямоугольного резервуара
| |||||||||
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
| |||||||||
Площадь поверхности усеченного конуса
| |||||||||
Площадь поверхности эллипсоида
| |||||||||
Площадь поверхности квадратной пирамиды
Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности тела
Площадь поверхности твердого тела является мерой общей площади, занимаемой поверхностью объекта. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах Калькулятор объема и Калькулятор площади. Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для более подробной информации о каждом отдельном объекте.
Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах Калькулятор объема и Калькулятор площади. Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для более подробной информации о каждом отдельном объекте.
Сфера
Площадь поверхности (SA) сферы можно рассчитать с помощью уравнения:
SA = 4πr 2
где r радиус
Ксаэль не любит ни с кем делиться своими шоколадными трюфелями. Когда она получает коробку трюфелей Lindt, она начинает вычислять площадь поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую ей нужно облизать, чтобы уменьшить вероятность того, что кто-нибудь попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйма 2
Конус
Площадь поверхности круглого конуса можно рассчитать, суммируя площади поверхности каждого из его отдельных компонентов. «Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
«Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
основание SA = πr 2
боковой SA = πr√r 2 + h 2
общая SA = πr(r + √r 2 + h 2 )
где r — радиус, а h — высота. в ряде стран Юго-Восточной Азии. Она решает сшить свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных ниш шкафа, в котором оно находится. Она определяет площадь поверхности материала, которая ей нужна для создания шляпы радиусом 1 фут и высотой 0,5 фута, следующим образом:
поперечная SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 фута 2
Куб
Площадь поверхности куба можно рассчитать суммированием общая площадь его шести квадратных граней:
СА = 6а 2
где a — длина ребра
Анна хочет подарить своему младшему брату кубик Рубика на день рождения, но знает, что у ее брата короткая продолжительность концентрации внимания и он легко расстраивается. Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический бак
Площадь поверхности закрытого цилиндра можно рассчитать, суммируя площади его основания и боковой поверхности:
основание SA = 2πr 2
боковой SA = 2πrh
общая СА = 2πr(r + h)
где r — радиус, а h — высота
У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну. Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 фута и радиусом 3,5 фута.
общая SA = 2π × 3,5(3,5 + 5,5) = 197,920 футов 2
Прямоугольный резервуар
Площадь поверхности прямоугольного резервуара равна сумме площадей каждой из его сторон:
СА = 2лв + 2лв + 2вч
где l — длина, w — ширина, h — высота
Банана, старшая дочь в длинной череде банановых фермеров, хочет научить свою избалованную гнилую младшую сестру, Банан-Хлеб, урок о надежде и ожиданиях. Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 фута 2
Капсула
Площадь поверхности капсулы можно определить, объединив уравнения площади поверхности шара и площади боковой поверхности цилиндра. Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь поверхности рассчитывается следующим образом:
СА = 4πr 2 + 2πrh
где r радиус и h высота
Горацио производит плацебо, предназначенное для оттачивания индивидуальности, критического мышления и способности объективно и логически подходить к различным ситуациям. Он уже протестировал рынок и обнаружил, что подавляющее большинство населения из выборки не обладает ни одним из этих качеств и очень готово покупать его продукт, еще больше укореняясь в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле r размером 0,05 дюйма и h размером 0,5 дюйма:
Он уже протестировал рынок и обнаружил, что подавляющее большинство населения из выборки не обладает ни одним из этих качеств и очень готово покупать его продукт, еще больше укореняясь в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле r размером 0,05 дюйма и h размером 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 дюйма 2
Сферический колпачок
Площадь поверхности сферического колпачка составляет в зависимости от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание колпачка в расчет площади поверхности, где общая площадь поверхности представляет собой сумму площади основания и площади боковой поверхности сферического колпачка.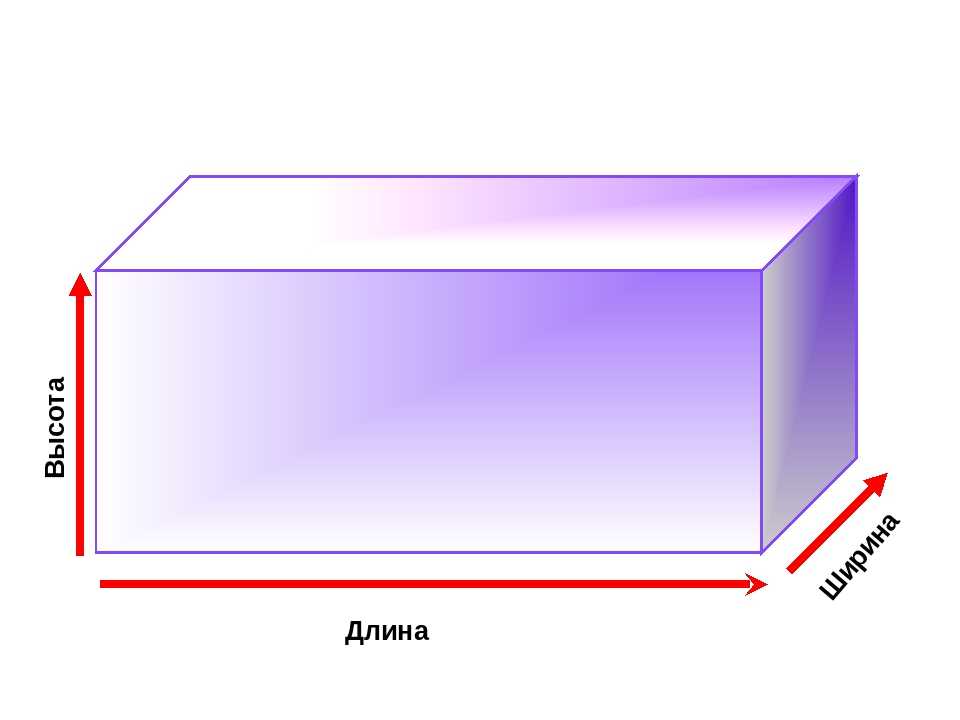 Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие:
Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие:
сферическая крышка SA = 2πRh
основание SA = πr 2
Общая твердая сфера SA = 2πRh + πr 2
где R — радиус сферического колпачка, r — радиус основания, h — высота
Дженнифер завидует глобусу, который ее старший брат Лоуренс получил на день рождения. Поскольку Дженнифер на две трети младше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с помощью 9.0402 R 0,80 фута и h 0,53 фута, как показано ниже:
SA = 2π × 0,80 × 0,53 = 2,664 фута 2
Усеченный конус
900 02 Площадь поверхности сплошного прямоконического усеченного конуса равна сумме площадей его двух круглых концов и площади его боковой поверхности: круглый конец SA = π(R 2 + r 2 )
боковой SA = π(R+r)√(R-r) 2 + h 2
общая SA = π(R 2 + r 2 ) + π(R+r)√(R-r) 2 + h 2
где R и r — радиусы концов, h — высота
Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки. Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде закрытого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R в 1 фут, r в 0,3 фута и h в 1,5 фута:
Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде закрытого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R в 1 фут, r в 0,3 фута и h в 1,5 фута:
всего SA = π(1 2 + 0,3 2 ) + π(1 + 0. 3) √(1 — 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Вычисление площади поверхности эллипсоида не имеет простой и точной формулы, такой как куб или другая более простая форма. Калькулятор выше использует приблизительную формулу, которая предполагает почти сферический эллипсоид:
SA ≈ 4π 1,6 √(a 1,6 b 1,6 + a 1,6 c 1,6 + b 1,6 c 1,6 )/3
где a , b и c — оси эллипса
Колтейн всегда любила готовить и недавно выиграла на конкурсе керамический нож. К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
SA ≈ 4π 1,6 √(0,1 1,6 0,2 1,6 + 0,1 1,6 0,35 1,6 + 0,2 1,6 0,35 1,6 )/3 = 0,562 дюйма 2
Квадратная пирамида
Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину ребра a , площадь поверхности можно рассчитать с помощью следующих уравнений:
база SA = 2
боковой SA = 2a√(a/2) 2 + h 2
всего SA = a 2 + 2a√(a/2) 2 + h 2
В классе Вонквайлы недавно завершилось строительство модели Великой пирамиды Гизы.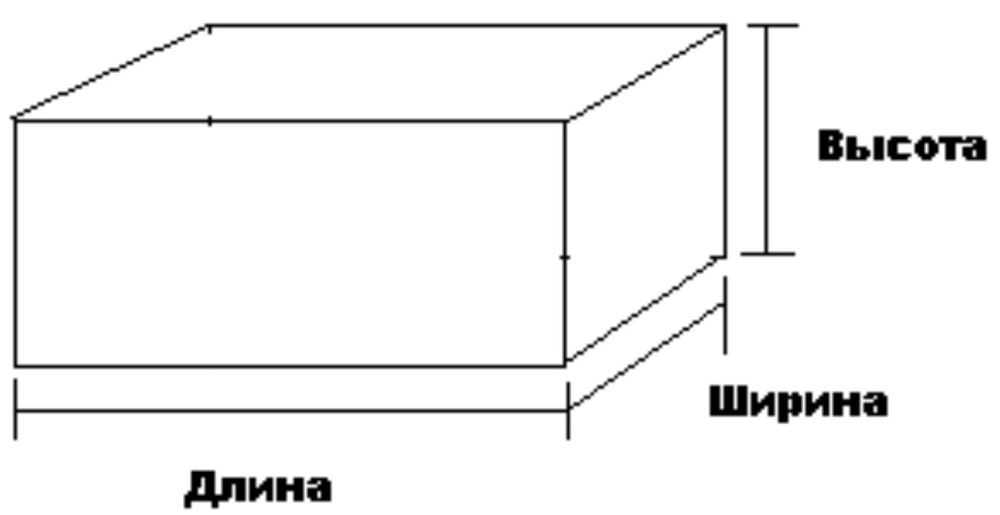

 д.
д.