Javascript целочисленное деление: Как поделить число нацело в javascript?

Содержание

Назначение деления (/=) Оператор присваивания division делит переменную на значение правого операнда присваивает результат Последнее изменение:Март 25,2022,автор MDN contributors

Деление (/)Оператор деления(/)образует коэффициент своих операндов,где левый операнд-делитель,а правый-делимое.

Оператор присваивания деления(/=)делит переменную на значение правого операнда и присваивает результат переменной.

Оператор /=сначала делит значение переменной или свойства (в левой части оператора)на значение выражения (в правой части оператора).Затем оператор присваивает переменной или свойству результат этой операции с плавающей точкой.

Присвоение (=)Простой оператор присваивания(=)используется для присвоения значения переменной.Операция присваивания оценивается по присвоенному значению.Для присвоения одного значения нескольким переменным можно использовать цепочку операторов присваивания.

Все числа в javascript являются двойными.Это означает,что по умолчанию целочисленное деление отсутствует.

Оператор присвоения деления ( /= ) делит переменную на значение правого операнда и присваивает результат переменной.

Try it

Syntax

x /= y // х = х / у

Examples

Использование задания на деление

// Предполагается, что следующая переменная и все операции выполняются по порядку
// бар = 5
bar /= 2     // 2.5
bar /= 2     // 1.25
bar /= 0     // Infinity
bar /= 'foo' // NaN

Specifications

Specification
Спецификация языка ECMAScript # sec-assignment-operators

Browser compatibility

	Desktop	Mobile	Server
	Chrome	Edge	Firefox	Internet Explorer	Opera	Safari	WebView Android	Chrome Android	Firefox для Android	Opera Android	Safari на IOS	Samsung Internet	Deno	Node. js
`Division_assignment`	1	12	1	3	3	1	4.4	18	4	10.1	1	1.0	1.0	0.10.0

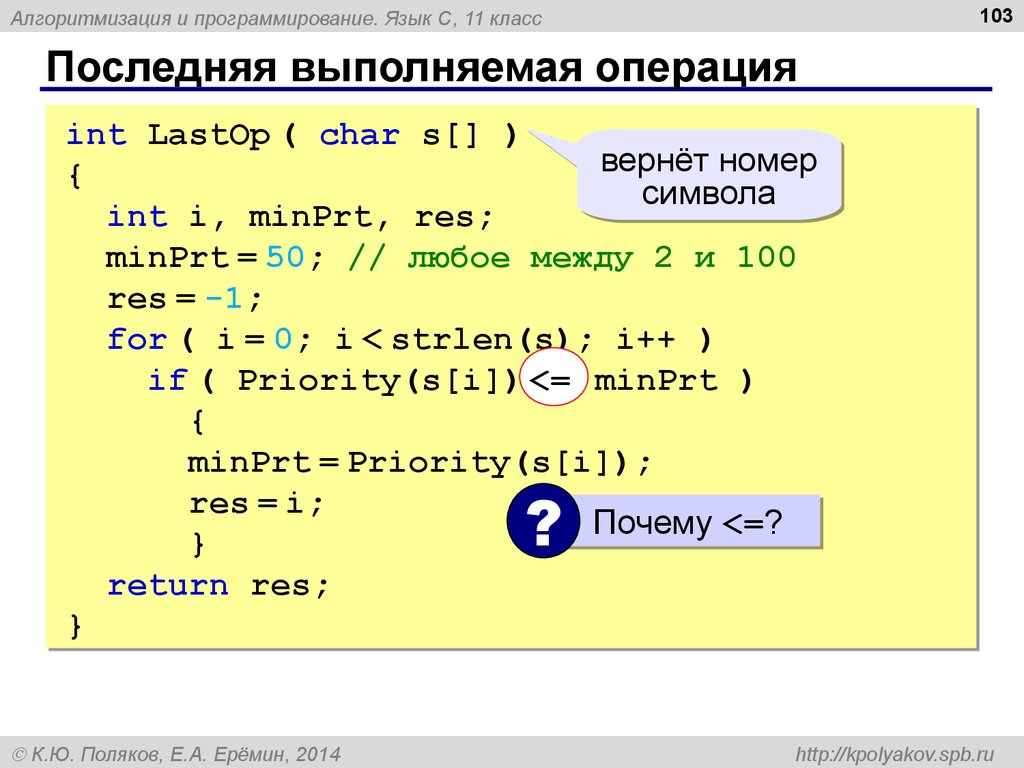
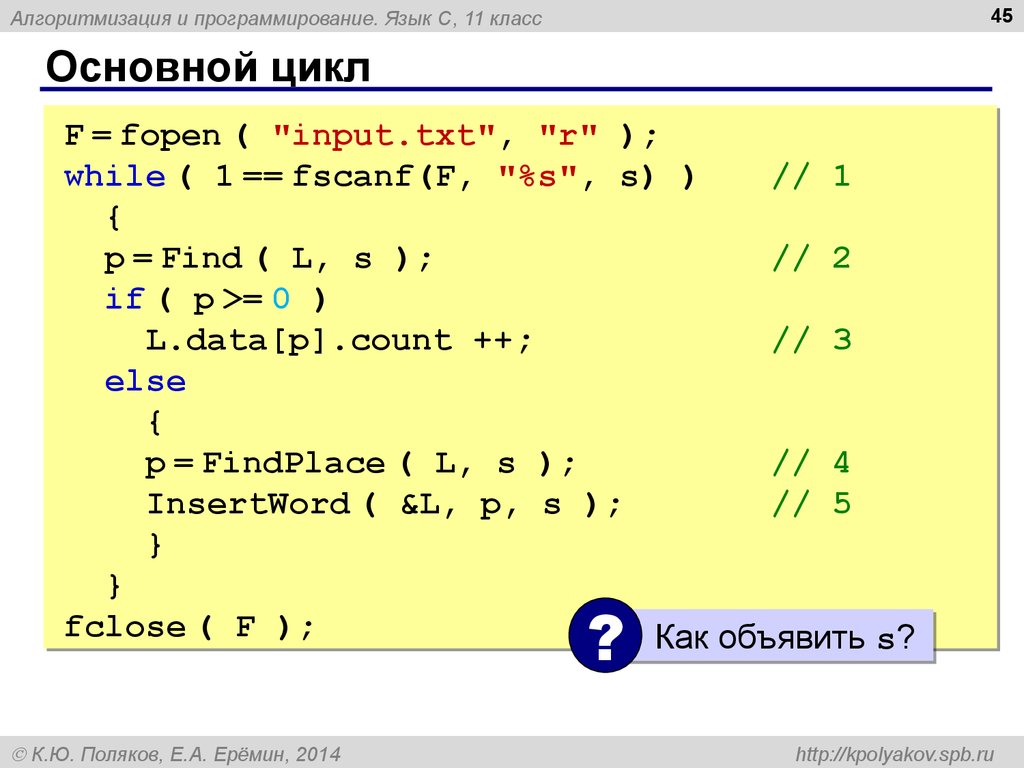
Операторы языка TRIK Studio — Руководство по работе с TRIK Studio

1
.
Бинарные операторы.
2
.
Унарные операторы.
3
.
Оператор присваивания.
4
.
Оператор возврата значения.
5
.
Пустой оператор.

Бинарные операторы

Title	Title	Title
	Сложение	Применимо к вещественным и целым значениям. Результат целый, если оба аргумента целые, иначе вещественный.
	Вычитание	Применимо к вещественным и целым значениям. Результат целый, если оба аргумента целые, иначе вещественный.
	Умножение	Применимо к вещественным и целым значениям. Результат целый, если оба аргумента целые, иначе вещественный.
	Деление	Применимо к вещественным и целым значениям. Результат вещественный.
	Целочисленное деление	Применимо к целым значениям. Результат целый.
	Возведение в степень	Применимо к вещественным и целым значениям. Результат вещественный.
	Остаток от деления	Применим к целым значениям. Результат целый.
	Побитовое «и»	Применимо к целым значениям. Результат целый.
	Побитовое «или»	Применимо к целым значениям. Результат целый.
>>, <<	Побитовые сдвиги вправо и влево	Применимы к целым значениям. Результат целый.
	Конкатенация	Применим к строковым значениям. Результат — строка.
>=, >, <, <=	Операции сравнения	Применимы к целым и вещественным значениям. Результат булевый.
	Операция проверки равенства	Применима к значениям любых типов. Результат булевый.
~=, !=, ‘~=’, ‘!=’	Операция проверки неравенства	Применима к значениям любых типов. Результат булевый. Альтернативные способы записи операции не различаются по смыслу.
and, &&	Логическое «и»	Применимо к целым, вещественным и булевым значениям. Результат булевый. Альтернативные способы записи операции по смыслу не различаются.
or, \|\|	Логическое «или»	Применимо к целым, вещественным и булевым значениям. Результат булевый. Альтернативные способы записи операции по смыслу не различаются.

Унарные операторы

Title	Title	Title
	Арифметический унарный минус	Применим к целым и вещественным значениям. Результат целый или вещественный (в зависимости от типа аргумента).
	Побитовое «не»	Применимо к целым значениям. Результат целый.
	Логическое «не»	Применимо к булевым, целым, вещественным и строковым значениям, результат булевый (0 или пустая строка считается false, всё остальное — true).
	Оператор взятия длины	Применим к строковым значениям. Результат целый.

Оператор присваивания

Имеет следующий вид:

переменная1, переменная2, …, переменнаяN = выражение1, выражение2, …, выражениеN

В самом простом виде переменная = выражение.

Оператор возврата значения

Записывается как обычное выражение и должен находиться в конце блока операторов.

Пустой оператор

Записывается как ;.

Пример

Блок операторов с двумя операторами присваивания и оператором возврата значения:

a, b = 1, 2; — оператор присваивания и пустой оператор

c = 3; — оператор присваивания и пустой оператор

a + b + c — оператор возврата значения

Python Integer Division [2-минутное руководство] — Finxter

Криса

5/5 — (1 голос)

Когда я начал изучать Python 3, меня смущала семантика деления двух целых чисел. Является ли результат значением с плавающей запятой или целым числом?

Причиной моего замешательства была неприятная ошибка Java, которую я однажды обнаружил в своем коде. Код должен был выполнять простое деление двух целых чисел, чтобы вернуть значение параметра между нулем и единицей. Но Java использует целочисленное деление, то есть пропускает остаток. Таким образом, значение всегда было либо нулем, либо единицей, но не промежуточным. Мне потребовались дни, чтобы понять это.

Сэкономьте время на отладку, раз и навсегда запомнив следующее правило.

Оператор с двойной обратной косой чертой // выполняет целочисленное деление, а оператор с одинарной обратной косой чертой

/ выполняет деление с плавающей запятой. Пример целочисленного деления: 40//11 = 3 . Пример деления с плавающей запятой: 40/11 = 3,6363636363636362 .

 >>> # Python 3
>>> 40//11
3
>>> 40/11
3,6363636363636362

Подробное описание Python Division

Посмотрите это видео на YouTube

Как работает целочисленное деление в Python?

Целочисленное деление состоит из двух шагов:

Выполнение нормального деления с плавающей запятой a / b.
Полученное число с плавающей запятой округлить до следующего целого числа.

Вот пример:

 х = 30 // 11
печать (х)
# 2

Целочисленное деление Python 2 vs 3

Python 2.x делит два целых числа на целочисленное деление , также известное как деление пола , потому что оно применяет функцию нижнего предела после обычного деления для «округления в меньшую сторону», поэтому оно оценивает выражение 5/2 до 2 . В Python 3 целочисленное деление выполняется с использованием двойной косой черты 5//2 , которая оценивается как 2 . Единственная передняя косая черта для деления пола «/» устарела в Python 2.2+ и Python 3.

Вот код для целочисленного деления в Python 2 с использованием оператора одиночной косой черты / :

 # Питон 2
печать(10/3)
# 3

А вот код целочисленного деления в Python 3 с использованием оператора двойной обратной косой черты // :

 # Python 3
печать(10//3)
# 3

Интерактивная оболочка + головоломка

Вы можете попробовать это в нашей интерактивной оболочке Python:

Упражнение : Что выводит этот фрагмент кода?

Хотя головоломка кажется простой, более двадцати процентов пользователей Finxter не могут ее решить. Вы можете проверить, правильно ли вы решили его здесь: Проверьте свои навыки прямо сейчас!

Арифметические операторы

Арифметические операторы — это синтаксические сокращения для выполнения основных математических операций над числами.

7 900

22

91015

8 **

Operator	Name	Description	Example
+	Addition	Calculating the sum of the two operands	`3 + 4 == 7`
–	Вычитание	Вычитание второго операнда из первого операнда	`4 - 3 == 1`
*	Multiplication	Multiplying the first with the second operand	`3 * 4 == 12`
/	Division	Dividing the first по второму операнду	`3 / 4 == 0,75`
%	Модуль	Вычисление остатка при делении первого на второй операнд
//	Целочисленное деление, напольное деление	Деление первого операнда на второй операнд и округление результата до следующего целого числа	`8 // 3 == 2`
Экспонента	Возведение первого операнда в степень второго операнда	`2 ** 3 == 8`

Крис

Май

Работая исследователем распределенных систем, доктор Кристиан нашел его любовь к обучению студентов информатики.

Чтобы помочь студентам достичь более высоких уровней успеха в Python, он основал образовательный веб-сайт по программированию Finxter.com. Он автор популярной книги по программированию Python One-Liners (NoStarch 2020), соавтор серии самостоятельно опубликованных книг Coffee Break Python, энтузиаст информатики, фрилансер и владелец одного из 10 крупнейших блогов Python в мире.

Его увлечения — писать, читать и программировать. Но его самая большая страсть — служить начинающим программистам через Finxter и помогать им повышать свои навыки. Вы можете присоединиться к его бесплатной академии электронной почты здесь.

Категории Информатика, Ежедневная головоломка Python, Структуры данных, Python, Операторы Python, Скрипты

Положительное число, деленное на отрицательное число

В этом видео-анимации и визуальных подсказках «Математика — это визуальная» мы концептуально исследуем отрицательное деление на целочисленное положительное деление с помощью конкретных и визуальных представлений! Мы также рассмотрим это с помощью двух подходов: квотного деления и партитивного деления!

Пока в целочисленном делении , мы взялись за следующие идеи:

Целое числовое деление и два типа деления: квотативный и партитивный
Деление целых чисел: отрицательное деление на отрицательное
Деление целых чисел: отрицательное деление на положительное

Если вы еще не просмотрели эти сообщения, обязательно вернитесь назад, прежде чем двигаться дальше, чтобы убедиться, что вы готовы понять наш последний шаг в серии «Деление целых чисел»: Положительное число, деленное на отрицательное число .

В этом видео мы рассмотрим деление положительного дивиденда на отрицательный делитель сначала с использованием долевого деления (или справедливой доли), а затем квотного (или измеренного) деления. Зрителю также будет предложено поставить видео на паузу и попробовать свое собственное, используя конкретные манипулятивы и/или визуальные эффекты.

См. приведенное ниже руководство, призванное помочь учителям и/или родителям использовать это задание со своими учениками/детями.

Визуальная подсказка №1: Раздел

В видео выше мы начинаем с деления негатива на негатив через разделительное деление:

8 ÷ (-2) = ___

прописью:

8 разделить на -2 группы дает результат ___ на группу

Итак, пусть зритель конкретно и/или визуально смоделирует следующее:

Мы можем приблизиться к этому, используя набор или пространственное разделение модели количество на 2 равные «отрицательно заряженные» группы и подсчет количества объектов в каждой группе. Мы можем думать об этом как о повторяющемся вычитании, если бы мы должны были честно разделить 1 объект за раз или 2 объекта за раз, до количества, которое учащийся может быстро заменить для распределения поровну между двумя группами.

Визуальная подсказка № 2: деление в кавычках

Теперь мы переходим к решению той же задачи с точки зрения партитивного деления:

0 3 ÷ (-900) = 1____
или
8 разделить на группы по -2 дает результат ____ групп.

Проблема, с которой мы здесь сталкиваемся, заключается в том, что мы хотим определить, сколько групп -2 мы можем создать из 8.

Это проблема, потому что мы не можем сделать группы из -2 (или так может показаться).

Если мы сначала определим, сколько групп +2 мы можем составить (всего 4), мы можем свести на нет отрицательное значение каждой группы, используя отрицательно заряженные группы: положительно заряженные группы +2, мы можем выразить эти группы как 4 отрицательно заряженные группы -2.

Другими словами, имеем:

-4 Группы -2

Другие возможные представления и стратегии:

Рассмотрим определение, сколько групп +2 мы можем « удалить », так как разделение представляет . Повторяемое подраздел . Как только мы узнаем, сколько групп +2 мы можем удалить, мы можем выразить эти группы отрицательно, чтобы создать отрицательные значения в группах:0003

Мы также можем подумать о том, сколько групп из -2 мы можем «сложить», чтобы получить 0:

Поскольку повторное сложение является операцией, противоположной многократному вычитанию, мы можем затем взять эти группы и «вычесть». их, отрицая группы:

Визуальная подсказка № 3: Ваша очередь!

Приостановите воспроизведение видео и позвольте зрителю применить свои знания о положительном числе, деленном на отрицательное число с использованием разделительное деление в следующей визуальной подсказке:

10 ÷ (-5) = ___
или
10, разделенных на -5 групп, дает результат ___ на группу.
Опять же, мы должны отметить, что мы хотим определить значение количества, которое будет разделено между 5 отрицательно заряженными группами или -5 группами.

При справедливом распределении 10 по -5 группам мы видим, что каждая группа будет содержать 2 отрицательных значения или -2.

Как насчет того, чтобы решить ту же задачу, используя деление в кавычках :
10 ÷ (-5) = ___
или
10 разделить на группы по -5 дает результат ___ групп

Используя наше концептуальное понимание, построенное с помощью предыдущих визуальных подсказок, мы теперь можем признать, что, поскольку существует 0 групп -5 мы можем создать из данных +10, мы должны использовать отрицательно заряженные группы.

Поскольку я могу создать 2 группы по +5, я знаю, что могу также представить те же две группы как -2 группы по -5.