Матрица перехода — Википедия
Материал из Википедии — свободной энциклопедии
В линейной алгебре базис векторного пространства размерности n{\displaystyle n} — это последовательность из n{\displaystyle n} векторов (α1,…,αn){\displaystyle (\alpha _{1},…,\alpha _{n})}, таких, что любой вектор пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов. При заданном базисе операторы представляются в виде квадратных матриц. Так как часто необходимо работать с несколькими базисами в одном и том же векторном пространстве, необходимо иметь правило перевода координат векторов и операторов из базиса в базис. Такой переход осуществляется с помощью матрицы перехода.
Если векторы b1,⋯,bn{\displaystyle \mathbf {b_{1}} ,\cdots ,\mathbf {b_{n}} } выражаются через векторы a1,⋯,an{\displaystyle \mathbf {a_{1}} ,\cdots ,\mathbf {a_{n}} } как:
- b1=α11a1+α12a2+…+α1nan{\displaystyle \mathbf {b} _{1}=\alpha _{11}\mathbf {a} _{1}+\alpha _{12}\mathbf {a} _{2}+\ldots +\alpha _{1n}\mathbf {a} _{n}}.
- b2=α21a1+α22a2+…+α2nan{\displaystyle \mathbf {b} _{2}=\alpha _{21}\mathbf {a} _{1}+\alpha _{22}\mathbf {a} _{2}+\ldots +\alpha _{2n}\mathbf {a} _{n}}.
- …{\displaystyle \ldots }.
- bn=αn1a1+αn2a2+…+αnnan{\displaystyle \mathbf {b} _{n}=\alpha _{n1}\mathbf {a} _{1}+\alpha _{n2}\mathbf {a} _{2}+\ldots +\alpha _{nn}\mathbf {a} _{n}}.
то матрица перехода от базиса (a1,⋯,an){\displaystyle (\mathbf {a_{1}} ,\cdots ,\mathbf {a_{n}} )} к базису (b1,⋯,bn{\displaystyle (\mathbf {b_{1}} ,\cdots ,\mathbf {b_{n}} }) будет:
- (α11α21…αn1α12α22…αn2…………α1nα2n…αnn){\displaystyle {\begin{pmatrix}\alpha _{11}&\alpha _{21}&…&\alpha _{n1}\\\alpha _{12}&\alpha _{22}&…&\alpha _{n2}\\…&…&…&…\\\alpha _{1n}&\alpha _{2n}&…&\alpha _{nn}\end{pmatrix}}}
При умножении матрицы, обратной к матрице перехода, на столбец, составленный из коэффициентов разложения вектора по базису a1,a2,…,an{\displaystyle a_{1},a_{2},\ldots ,a_{n}}, мы получаем тот же вектор, выраженный через базис b1,b2,…,bn{\displaystyle b_{1},b_{2},\ldots ,b_{n}}.
Пример[править | править код]
Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:
- [x′y′]=[cosθ−sinθsinθcosθ][xy]{\displaystyle {\begin{bmatrix}x’\\y’\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}
Найдём матрицу перехода от базиса a1=(12−1),a2=(−1−42),a3=(510){\displaystyle a_{1}={\begin{pmatrix}1\\2\\-1\end{pmatrix}},a_{2}={\begin{pmatrix}-1\\-4\\2\end{pmatrix}},a_{3}={\begin{pmatrix}5\\1\\0\end{pmatrix}}} к единичному базису b1=(100),b2=(010),b3=(001){\displaystyle b_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},b_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},b_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}} путём элементарных преобразований
(1−151002−41010−120001)→(1002−10−190101−5−9001012){\displaystyle \left({\begin{array}{ccc|ccc}1&-1&5&1&0&0\\2&-4&1&0&1&0\\-1&2&0&0&0&1\end{array}}\right)\rightarrow \left({\begin{array}{ccc|ccc}1&0&0&2&-10&-19\\0&1&0&1&-5&-9\\0&0&1&0&1&2\end{array}}\right)} следовательно Pa→b=(2−10−191−5−9012){\displaystyle P_{a\rightarrow b}={\begin{pmatrix}2&-10&-19\\1&-5&-9\\0&1&2\end{pmatrix}}}
Затерянная документация или transform: matrix3d [перевод] / Habr
Когда погружаешься в документацию о CSS3 transform: matrix3d, находишь короткое определение «Задает 3D трансформацию как матрицу 4х4.», сопровождаемое определением функции в виде:matrix3d(m00, m01, m02, m03,
m10, m11, m12, m13,
m20, m21, m22, m23,
m30, m31, m31, m33)
И если не являешься Богом математики, скорее всего, внутри возникает беспокойство о недостатке документации, за которым следует вопрос, как создать по-настоящему крутую штуку? Описанный подход не претендует называться математическим или полным — я всего лишь пытаюсь заполнить маленькую брешь документации.
демо | первоисточник
Немного линейной алгебры
Всякая комплексная трансформация может быть представленна тремя базовыми:
Поворот (rotate)
Масштабирование (scale)
Перемещение (translate)
Эти 3 базовых преобразования могут быть совмещены в одну огромную всеобъемлющую матрицу трансформации. Пока все просто, но как перейти от 3 базовых этапов к тому необузданному списку параметров, который нужен для matrix3d? Давайте начнем с самой простой матрицы в математике (чтобы упростить себе жизнь я использую Sylvester для математических операций с матрицами).
Единичная матрица
Эта матрица не делает ничего! Nil! Null! Nada! Ни один пиксель не пострадал! Я разделил эту матрицу на 2 секции. Красная секция это область где описываются Поворот (Rotate) и Масштабирование (Scale). В желтой секции описывается cдвиг или перемещение (translate). Остальные параметры используются очень редко, за исключением понастоящему странных FX демок в LSD стиле.
Мы начнем созданием матрицы масштабирования, умножив единичную матрицу на коэффициент масштабирования.
scaleMatrix = indentityMatrix.multiply(s)
Матрица масштабирования
scaleMatrix = $M([
[s,0,0,0],
[0,s,0,0],
[0,0,s,0],
[0,0,0,s]
])
Так как мы не хотим трансформировать координаты перемещения (translate), давайте заменим последний параметр масштабирования на 1:
scaleMatrix = $M([
[s,0,0,0],
[0,s,0,0],
[0,0,s,0],
[0,0,0,1]
])
Матрицы поворота (Rotate)
Поворот может осуществляться вокруг собственной оси X, Y, Z на заданный угол. Давайте примем значения углов для каждой оси как a, b, c. Соотвествующие матрицы, представляющие такую трансформацию:
rotationXMatrix = $M([
[1,0,0,0],
[0,Math.cos(a), Math.sin(-a), 0],
[0,0,0,1]
])
rotationYMatrix = $M([
[Math.cos( b), 0, Math.sin(b),0],
[0,1,0,0],
[Math.sin(-b), 0, Math.cos(b), 0],
[0,0,0,1]
])
rotationZMatrix = $M([
[Math.cos( c), Math.sin(-c), 0, 0],
[Math.sin( c), Math.cos( c), 0, 0],
[0,0,1,0],
[0,0,0,1]
])
Каждая матрица описывает поворот вокруг одной оси.
Матрица перемещения (translate)
translationMatrix = $M([
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[tx,ty,tz,1]
])
Матрица перемещения не затрагивает большенство пикселей, но добавляет значения tx, ty и tz к результирующему вектору направления.
Веселье
Да, математика может быть развлечением, а каждая из этих матриц может быть использованна в композиции. Итак, если нужно повернуть что-нибудь вокруг каждой оси и потом переместить это на несколько пикселей, просто перемножте эти матрицы. Вот и все:
.x(rotationYMatrix)
.x(rotationZMatrix)
.x(scaleMatrix)
.x(translationMatrix)
И в конце применим трансформацию к изображению:
s = «matrix3d(»
s += tM.e(1,1).toFixed(10) + «,» + tM.e(1,2).toFixed(10) + «,» + tM.e(1,3).toFixed(10) + «,» + tM.e(1,4).toFixed(10) + «,»
s += tM.e(2,1).toFixed(10) + «,» + tM.e(2,2).toFixed(10) + «,» + tM.e(2,3).toFixed(10) + «,» + tM.e(2,4).toFixed(10) + «,»
s += tM.e(3,1).toFixed(10) + «,» + tM.e(3,2).toFixed(10) + «,» + tM.e(3,3).toFixed(10) + «,» + tM.e(3,4).toFixed(10) + «,»
s += tM.e(4,1).toFixed(10) + «,» + tM.e(4,2).toFixed(10) + «,» + tM.e(4,3).toFixed(10) + «,» + tM.e(4,4).toFixed(10)
s += «)»
document.getElementById(‘darth-vader’).style[‘-webkit-transform’] = s
Предостережения
Первое — если погуглить линейную трансформацию и найти примеры таких матриц, можно удивится что матрицы немного отличаются. Дело в том, что CSS матрица транспонированная — вот так просто, выполните транспонирование матрицы и она должна работать. Второе — CSS не поддерживает научную форму числа (например 123е-15) в качестве параметров — поэтому нужно использовать toFixed(numberOfDigits) чтобы нормализовать их.
Среда разработки
Подход работает в -webkit- браузерах, таких как Chrome или Safari, Firefox 10+ и IE 10. Префиксы можно посмотреть здесь caniuse.com/transforms3d. Демо работает только в -webkit- и написанно на coffeescript который немного круче javascript — но скомплилированный код должен быть читабельным. Вы можете забрать весь урок и исходники на github.
Демо
Оригинал статьи
Facebook автора
Twitter автора
Потрясающая Javascript библиотека Sylvester
Статья о линейных трансформациях на Wikipedia
Матрица преобразований
Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.
Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме [x y 1]. Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.
Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:
Координатные преобразования выражаются в виде матричных умножений:
Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:
Единичная матрица
Единичной матрицей называется, та у которой значения матрицы a и d равны 1, а остальные равны 0. Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.
Масштабирование
Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.
Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.
Высчитываем новые координаты объекта:
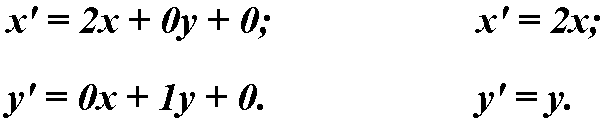
Отражение
Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1, по вертикали d = -1. Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.
Наклон
Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.
Например: Для наклона объекта по вертикали вверх установим значение b = 1
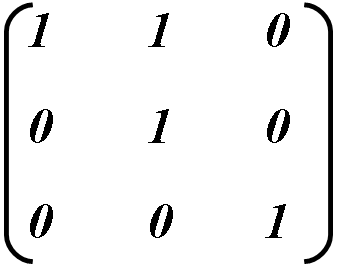
Высчитываем новые координаты объекта:
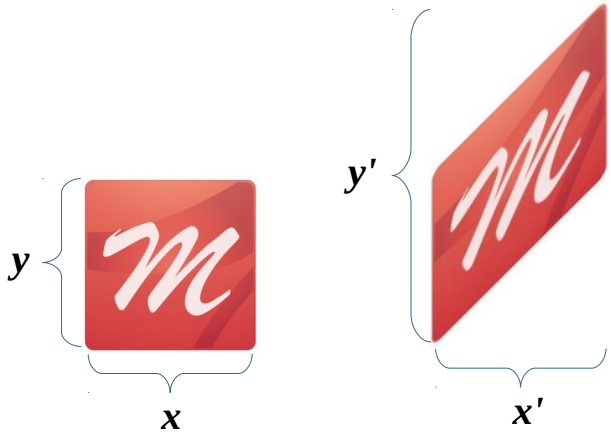
В итоге к наклону объекта приводит только координата y, которая увеличивается на значение x.
Поворот
Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.
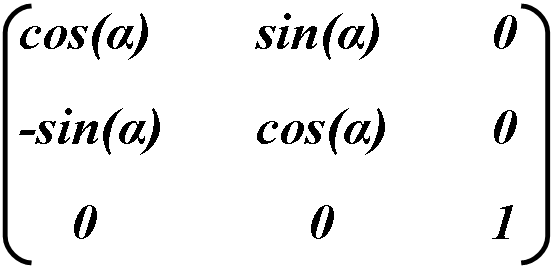
Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.
Перемещение
Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.
Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке Геометрия.
Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF [a b c d e f]. Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:
- Перемещения указываются как [1 0 0 1 tx ty], где tx и ty — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
- Масштабирование указывается как [sx 0 0 sy 0 0]. Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и sx и sy единиц в старой координатной системе соответственно.
- Повороты производятся матрицей [cosθ sinθ −sinθ cosθ 0 0], что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
- Наклон указывается как [1 tanα tanβ 1 0 0], что соответствует наклону оси x на угол α и оси y на угол β.
На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.
Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.
В таблице ниже приведены допустимые преобразования и значения матрицы.
Несмотря на все выше сказанное, матрица преобразований очень простой и эффективный инструмент для трансформации. Конечно, применять ее, например, для поворота нецелесообразно, так как во вкладке Геометрия имеется функция Поворот, но для отражения объекта она просто необходима.
Элементарные преобразования матрицы — Википедия
Материал из Википедии — свободной энциклопедии
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями строк называют:
- перестановку местами любых двух строк матрицы;
- умножение любой строки матрицы на константу k{\displaystyle k}, k≠0{\displaystyle k\neq 0}, при этом определитель матрицы увеличивается в k раз;
- прибавление к любой строке матрицы другой строки, умноженной на некоторую константу.
В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу k{\displaystyle k}, k≠0{\displaystyle k\neq 0} и прибавление к любой строке матрицы другой строки, умноженной на константу k{\displaystyle k}, k≠0{\displaystyle k\neq 0}.
Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение A∼B{\displaystyle A\sim B} указывает на то, что матрица A{\displaystyle A} может быть получена из B{\displaystyle B} путём элементарных преобразований (или наоборот).
Инвариантность ранга при элементарных преобразованиях[править | править код]
 | Теорема (об инвариантности ранга при элементарных преобразованиях). Если A∼B{\displaystyle A\sim B}, то rangA=rangB{\displaystyle \mathrm {rang} A=\mathrm {rang} B}. |
Эквивалентность СЛАУ при элементарных преобразованиях[править | править код]
- Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:
- перестановку уравнений;
- умножение уравнения на ненулевую константу;
- сложение одного уравнения с другим, умноженным на некоторую константу.
- То есть элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
| Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей. |
- Напомним, что две системы называются эквивалентными, если множества их решений совпадают.
Нахождение обратных матриц[править | править код]
Приведение матриц к ступенчатому виду[править | править код]
Просмотреть статью: Ступенчатый вид по строкам
- Введём понятие ступенчатых матриц:
- Матрица A{\displaystyle A} имеет ступенчатый вид, если:
- Все нулевые строки матрицы A{\displaystyle A} стоят последними;
- Для любой ненулевой строки матрицы A{\displaystyle A} (пусть для определённости её номер равен k{\displaystyle k}) справедливо следующее: если akj{\displaystyle a_{kj}} — первый ненулевой элемент строки k{\displaystyle k}, то ∀i,l:i>k,l≤jail=0{\displaystyle \forall i,l:\;i>k,\;l\leq j\quad a_{il}=0}.
- Все нулевые строки матрицы A{\displaystyle A} стоят последними;
- Тогда справедливо следующее утверждение:
| Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
Элементарная матрица. Матрица А является элементарной, если умножение на неё произвольной матрицы В приводит к элементарным преобразованиям строк в матрице В.
- Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
Разложение матрицы аффинного преобразования / Habr
Не так давно в процессе разработки редактора 2D-графики возникла задача разложить матрицу аффинного преобразования на плоскости, на произведение матриц простых преобразований с тем, чтобы отобразить их пользователю и предложить какую-то более-менее адекватную интерпретацию того, что произошло с объектом на канвасе. Честно говоря, эта задача вызвала у меня определенные трудности. Университет я закончил уже давно, и мне было непонятно, а возможно ли это сделать в принципе, учитывая, что исходная матрица могла быть результатом произвольной последовательности сдвигов, масштабов, поворотов, и переносов, причем каждое преобразование могло иметь свой произвольный центр. И, во-вторых, непонятно было, как найти семь параметров, имея всего шесть коэффициентов матрицы. Ключом к решению этой задачи оказалась статья «Разложение матрицы центроаффинного преобразования для нормализации изображения»¹, в которой рассматривается такая же задача, но без учета преобразования переноса и для преобразований относительно центра координат. Далее я фактически просто адаптирую результаты этой статьи с учетом переноса и для произвольного центра преобразований.Итак, пусть матрица, задающая произвольное преобразование на плоскости, имеет вид:
┌ ┐
│ a11 a12 0 │
M = │ a21 a22 0 │.
│ a31 a32 1 │
└ ┘Ее определитель
det = a11⋅a22 - a12⋅a21, det ≠ 0.Пусть точка на плоскости задается вектор-строкой вида (x, y, 1), а ее преобразование – умножением справа на матрицу преобразования:
┌ ┐
┌ ┐ │ a11 a12 0 │
p1 = p0 • M = │ x0 y0 1 │ • │ a21 a22 0 │
└ ┘ │ a31 a32 1 │
└ ┘В упомятнутой выше статье¹ утверждается, что произвольная матрица M центроаффинного преобразования может быть представлена как произведение матриц R поворота, матрицы Hx сдвига вдоль оси X и матрицы S масштабирования:
Mc = R • Hx • SЗдесь
┌ ┐
│ cos(α) sin(α) 0 │
R = │ -sin(α) cos(α) 0 │,
│ 0 0 1 │
└ ┘
┌ ┐
│ 1 hx 0 │
Hx = │ 0 1 0 │,
│ 0 0 1 │
└ ┘
┌ ┐
│ sx 0 0 │
S = │ 0 sy 0 │,
│ 0 0 1 │
└ ┘При разложении произвольной матрица аффинного преобразования необходимо привести центр трансформации к центру координат, а также учесть преобразование переноса:
M = T0 • S • H • R • T0⁻¹ • T,
┌ ┐
│ 1 0 0 │
T0 = │ 0 1 0 │,
│ -tx0 -ty0 1 │
└ ┘
┌ ┐
│ 1 0 0 │
T0⁻¹ = │ 0 1 0 │,
│ tx0 ty0 1 │
└ ┘
┌ ┐
│ 1 0 0 │
T = │ 0 1 0 │.
│ tx ty 1 │
└ ┘Подставив выражения для матриц простых преобразований получим следующие выражения для коэффициентов M:
a11 = sx⋅cos(α) - sx⋅hx⋅sin(α)
a12 = sx⋅hx⋅cos(α) + sx⋅sin(α)
a21 = -sy⋅sin(α)
a22 = sy⋅cos(α)
a31 = tx + tx0⋅(1 - (sx⋅cos(α) - sx⋅hx⋅sin(α))) + ty0⋅sy⋅sin(α)
= tx + tx0⋅(1 - a11) - ty0⋅a21
a32 = ty + ty0⋅(1 - cos(α)⋅sy) - tx0⋅(sx⋅hx⋅cos(α) + sx⋅sin(α))
= ty + ty0⋅(1 - a22) - tx0⋅a12Решая данные уравнения относительно sx, sy, α, hx, tx, ty, после некоторых упрощений, получим выражения для искомых параметров:
if a22=0
α = π/2,
sy = -a21
else
α = atan(-a21/a22),
sy = a22/cos(α),
sx = det(M)/sy,
hx = (a11⋅a21 + a12⋅a22)/det,
tx = a31 + ty0⋅a21 + tx0⋅(a11 - 1),
ty = a32 + tx0⋅a12 + ty0⋅(a22 - 1).Выражения для α, sx, sy, hx сооветствуют аналогичным в статье¹, хотя и несколько отличаются от них по форме. Кроме того мы получили формулы расчета параметров преобразования переноса tx и ty. Хочется также заметить, что даже если в оригинальной последовательности присутствовали сдвиги вдоль обеих осей, в разложении достаточно лишь сдвига вдоль одной из осей (здесь – вдоль оси X). Кроме того, поскольку угол поворота определен как результат функиции арктангенса, он принципиально ограничен значениями от -90˚ до +90˚. Учитывая также, что угол поворота на 180˚ соответсвует sx=-1 и sx=-1, мы имеем здесь некоторую неоднозначность. Например, изначально имея поворот на 120˚ при разложении по данному алгоритму мы получим -60˚ и sx=sy=-1.
¹) Путятин Е.П., Яковлева Е.В., Любченко В.А. «Разложение матрицы центроаффинного преобразования для нормализации изображения»
Развитие и трансформация матрицы
Вы уже знаете, что матрица способна измениться
И сегодня поговорим о том, как это происходит
Всего есть три варианта развития. Какой из них ваш — зависит от ресурса. А им могут стать сектора «характер», «долг», «труд» и «удача»
Именно они меняют привычки и картину мира в целом
.
Итак, правила перехода: 
11= 8 и наоборот 8 = 11 6 = 7 и наоборот 7 = 6
Классическая трансформация, когда «11» из вашего характера превращается в 8! Сразу оговорюсь, что в таком «переходе» редко участвуют характер 1 и 11. Как это происходит? Стресс, сложности в жизни, ранняя самостоятельность, рождение детей, одиночество и многое другое, что так или иначе влияет на нашу духовность, милосердие и сострадание.
Или же это возраст. Если есть ресурс (характер), матрица меняется с возрастом всегда! Поэтому в старости человек значительно добрее, на все смотрит с милосердием, умеет терпеть, всех понимает, растёт его духовность и желание быть ближе к религии.Даже наше отношение к смерти проще: если есть 88/888/8888, человек принимает эту мысль
Рост сознания. Переход из 6/66/666 в 7/77/777. Такой переход происходит в возрасте, который всем известен как «кризис среднего возраста» в 35 -38 лет. Старые установки теряют смысл и значение, зато открываются два новых пути!
Первый — понимание религии: вселенная вдруг становится проще, и вы резко понимаете, как в мире все устроено. Второй путь: совершая переход из сектора труд «6» в сектор удача 7, ослабляется сектор быт (1/2), и деньги перестают быть вашей целью
А сочетание 7 + 1/2 быт — это ещё и риск для развития зависимостей.
Обратное развитие. Когда вам не хватает амбиций, и вы это понимаете, когда однажды ваше милосердие начинает вам мешать, или вы попадаете в условия, в которых ваша «8» переходит в «11» в характере. Вообще, это каждый день происходит с нами само собой! Например, в моменты, когда мы отстаиваем свою точку зрения или хотим добиться цели любой ценой Но это состояние может стать и вашим естественным. Например, мужчина с характером 11 и долг 88 мог достигнет большего, если переведёт свои «8» в дополнительные 1111
Матрица поворота — Википедия
Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в двумерном пространстве[править | править код]
В двумерном пространстве поворот можно описать одним углом θ{\displaystyle \;\theta } со следующей матрицей линейного преобразования в декартовой системе координат:
- M(θ)=(cosθ∓sinθ±sinθcosθ){\displaystyle M(\theta )={\begin{pmatrix}\cos {\theta }&\mp \sin {\theta }\\\pm \sin {\theta }&\cos {\theta }\end{pmatrix}}}
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
- [x′y′]=[cosθ∓sinθ±sinθcosθ][xy].{\displaystyle {\begin{bmatrix}x’\\y’\\\end{bmatrix}}={\begin{bmatrix}\cos \theta &\mp \sin \theta \\\pm \sin \theta &\cos \theta \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}.}
Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:
- x′=xcosθ∓ysinθ,{\displaystyle x’=x\cos \theta \mp y\sin \theta ,}
- y′=±xsinθ+ycosθ.{\displaystyle y’=\pm x\sin \theta +y\cos \theta .}
Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).
Матрица поворота в трёхмерном пространстве[править | править код]
Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α{\displaystyle \alpha } в трёхмерном пространстве с неподвижной системой координат являются:
- Вращение вокруг оси x{\displaystyle x}:
- Mx(α)=(1000cosα−sinα0sinαcosα).{\displaystyle M_{x}(\alpha )={\begin{pmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{pmatrix}}.}
- Вращение вокруг оси y{\displaystyle y}:
- My(α)=(cosα0sinα010−sinα0cosα).{\displaystyle M_{y}(\alpha )={\begin{pmatrix}\cos \alpha &0&\sin \alpha \\0&1&0\\-\sin \alpha &0&\cos \alpha \end{pmatrix}}.}
- Вращение вокруг оси z{\displaystyle z}:
- Mz(α)=(cosα−sinα0sinαcosα0001).{\displaystyle M_{z}(\alpha )={\begin{pmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}.}
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси[2]. Например, при повороте на угол α=90∘{\displaystyle \alpha =90^{\circ }} вокруг оси z{\displaystyle z} ось x{\displaystyle x} переходит в y{\displaystyle y}: Mz(90∘)⋅ex=ey{\displaystyle M_{z}(90^{\circ })\cdot \mathbf {e} _{x}=\mathbf {e} _{y}}. Аналогично, My(90∘)⋅ez=ex{\displaystyle M_{y}(90^{\circ })\cdot \mathbf {e} _{z}=\mathbf {e} _{x}} и Mx(90∘)⋅ey=ez{\displaystyle M_{x}(90^{\circ })\cdot \mathbf {e} _{y}=\mathbf {e} _{z}}. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Матрица поворота в n{\displaystyle n}-мерном пространстве[править | править код]
Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.
Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.
Итак, совершенно аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.
Например:
- M1,2(α)=(cosα−sinα000sinαcosα000001000001000001){\displaystyle M_{1,2}(\alpha )={\begin{pmatrix}\cos \alpha &-\sin \alpha &0&0&0\\\sin \alpha &\cos \alpha &0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{pmatrix}}}
— матрица поворота в 5-мерном пространстве в плоскости x1x2{\displaystyle x_{1}x_{2}},
- M2,4(α)=(10000000cosα0−sinα00000100000sinα0cosα000000010000000100000001){\displaystyle M_{2,4}(\alpha )={\begin{pmatrix}1&0&0&0&0&0&0\\0&\cos \alpha &0&-\sin \alpha &0&0&0\\0&0&1&0&0&0&0\\0&\sin \alpha &0&\cos \alpha &0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\end{pmatrix}}}
— матрица поворота в 7-мерном пространстве в плоскости x2x4{\displaystyle x_{2}x_{4}}.
- При таком подходе знаки перед синусами расставлять даже легче, поскольку они определяются порядком перечисления осей плоскости вращения: какая названа первой, в той строке перед синусом минус.
- Легко видеть, что матрица поворота в плоскости x1x2{\displaystyle x_{1}x_{2}} совпадает (что естественно) с матрицей поворота в плоскости x2x1{\displaystyle x_{2}x_{1}} и т. д. с точностью до замены угла поворота на противоположный.
- Поэтому такие матрицы с переставленными индексами очевидно не независимы, и для получения произвольного поворота достаточно включить в композицию каждую плоскость только один раз, то есть, скажем, только M1,2(α1,2){\displaystyle M_{1,2}(\alpha _{1,2})}, а не M1,2(α1,2){\displaystyle M_{1,2}(\alpha _{1,2})} и M2,1(α2,1){\displaystyle M_{2,1}(\alpha _{2,1})}.
- Исходя из этого, нетрудно сосчитать их общее количество: n(n−1)/2{\displaystyle n(n-1)/2}, где n — размерность пространства.
Пусть M{\displaystyle \;M} — матрица поворота вокруг оси с ортом n{\displaystyle \;n} на угол α{\displaystyle \;\alpha }, M′{\displaystyle \;M’} — матрица поворота вокруг оси с ортом n′{\displaystyle \;n’} на тот же угол, причем
- n′=M″⋅n,{\displaystyle \;n’=M»\cdot \;n,}
где M″{\displaystyle \;M»} — матрица поворота, изменяющая орт оси поворота n{\displaystyle \;n}. Тогда
- M′=M″⋅M⋅M″T,{\displaystyle M’=M»\cdot M\cdot M»^{\;T},}
где M″T{\displaystyle \;M»^{\;T}} — транспонированная матрица M″{\displaystyle \;M»}.
Если M1{\displaystyle \;M_{1}} — матрица поворота вокруг оси с ортом n{\displaystyle \;n} на угол α{\displaystyle \;\alpha }, M2{\displaystyle \;M_{2}} — матрица поворота вокруг оси с ортом m{\displaystyle \;m} на угол β{\displaystyle \;\beta }, то M2⋅M1{\displaystyle M_{2}\cdot M_{1}} — матрица, описывающая поворот, являющийся результатом двух последовательно осуществленных поворотов (M1{\displaystyle \;M_{1}} и M2{\displaystyle \;M_{2}}), поскольку
- (M2⋅M1)⋅r=M2⋅(M1⋅r).{\displaystyle (M_{2}\cdot M_{1})\cdot r=M_{2}\cdot (M_{1}\cdot r).}
При этом последовательность поворотов можно поменять, видоизменив поворот M1{\displaystyle \;M_{1}}:
- M2⋅M1=M1′⋅M2,{\displaystyle M_{2}\cdot M_{1}=M’_{1}\cdot M_{2},}
где матрица M1′{\displaystyle \;M’_{1}} — матрица поворота на угол α{\displaystyle \;\alpha } вокруг оси c ортом n′,{\displaystyle \;n’,} повернутым с помощью поворота M2{\displaystyle \;M_{2}}:
- n′=M2⋅n,M1′=M2⋅M1⋅M2T,{\displaystyle n’=M_{2}\cdot n,\qquad M’_{1}=M_{2}\cdot M_{1}\cdot M_{2}^{T},}
поскольку M2T⋅M2=E{\displaystyle M_{2}^{T}\cdot M_{2}=E}, так как матрица поворота является ортогональной матрицей (E{\displaystyle \;E} — единичная матрица). Заметим, что коммутативности поворотов в обычном смысле нет, то есть
- M2⋅M1≠M1⋅M2.{\displaystyle M_{2}\cdot M_{1}\neq M_{1}\cdot M_{2}.}
Последовательные повороты около осей Z,X′,Z″{\displaystyle \;Z,X’,Z»} на угол прецессии (α{\displaystyle \alpha }), угол нутации (β{\displaystyle \beta }) и на угол собственного вращения (γ{\displaystyle \gamma }) приводят к следующему выражению для матрицы поворота:
- M(α,β,γ)=(cosαcosγ−sinαcosβsinγ−cosαsinγ−sinαcosβcosγsinαsinβsinαcosγ+cosαcosβsinγ−sinαsinγ+cosαcosβcosγ−cosαsinβsinβsinγsinβcosγcosβ).{\displaystyle M(\alpha ,\beta ,\gamma )={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &\sin \alpha \sin \beta \\\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &-\cos \alpha \sin \beta \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{pmatrix}}.}
Ось X′{\displaystyle \;X’} — ось X, повёрнутая первым поворотом (на α{\displaystyle \;\alpha }), Z″{\displaystyle \;Z»} — ось Z, повёрнутая первым и вторым поворотом (на α{\displaystyle \;\alpha } и β{\displaystyle \;\beta }). Вследствие перестановочности поворотов приведённая матрица соответствует поворотам на углы γ{\displaystyle \;\gamma }, β{\displaystyle \;\beta }, α{\displaystyle \;\alpha } вокруг осей Z, X, Z:
- M(α,β,γ)=MZ(α)⋅MX(β)⋅MZ(γ){\displaystyle M(\alpha ,\beta ,\gamma )=M_{Z}(\alpha )\cdot M_{X}(\beta )\cdot M_{Z}(\gamma )}.
В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:
- 1) Поворот около осей: X,Y,X{\displaystyle X,Y,X}
- 2) Соответственно: X,Y,Z{\displaystyle X,Y,Z}
- 3) X,Z,X{\displaystyle X,Z,X}
- 4) X,Z,Y{\displaystyle X,Z,Y}
- 5) Y,X,Y{\displaystyle Y,X,Y}
- 6) Y,X,Z{\displaystyle Y,X,Z}
- 7) Y,Z,X{\displaystyle Y,Z,X}
- 8) Y,Z,Y{\displaystyle Y,Z,Y}
- 9) Z,X,Y{\displaystyle Z,X,Y}
- 10) Z,X,Z{\displaystyle Z,X,Z}
- 11) Z,Y,X{\displaystyle Z,Y,X}
- 12) Z,Y,Z{\displaystyle Z,Y,Z}
Матрица поворота вокруг произвольной оси[править | править код]
Пусть ось вращения задана единичным вектором v^=(x,y,z){\displaystyle {\hat {\mathbf {v} }}=(x,y,z)}, а угол поворота θ{\displaystyle \theta }.
Тогда матрица поворота в декартовых координатах имеет вид:
- M(v^,θ)=(cosθ+(1−cosθ)x2(1−cosθ)xy−(sinθ)z(1−cosθ)xz+(sinθ)y(1−cosθ)yx+(sinθ)zcosθ+(1−cosθ)y2(1−cosθ)yz−(sinθ)x(1−cosθ)zx−(sinθ)y(1−cosθ)zy+(sinθ)xcosθ+(1−cosθ)z2){\displaystyle M({\hat {\mathbf {v} }},\theta )={\begin{pmatrix}\cos \theta +(1-\cos \theta )x^{2}&(1-\cos \theta )xy-(\sin \theta )z&(1-\cos \theta )xz+(\sin \theta )y\\(1-\cos \theta )yx+(\sin \theta )z&\cos \theta +(1-\cos \theta )y^{2}&(1-\cos \theta )yz-(\sin \theta )x\\(1-\cos \theta )zx-(\sin \theta )y&(1-\cos \theta )zy+(\sin \theta )x&\cos \theta +(1-\cos \theta )z^{2}\end{pmatrix}}}
Если задан кватернион q=(w,x,y,z){\displaystyle q=(w,x,y,z)}, то соответствующая матрица поворота имеет вид:
- Q=[1−2y2−2z22xy−2zw2xz+2yw2xy+2zw1−2×2−2z22yz−2xw2xz−2yw2yz+2xw1−2×2−2y2].{\displaystyle Q={\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}.}
Если M{\displaystyle \mathbf {M} } — матрица, задающая поворот вокруг оси n→{\displaystyle {\vec {n}}} на угол φ{\displaystyle \varphi }, то:
- |Mv→|=|v→|{\displaystyle |\mathbf {M} {\vec {v}}|=|{\vec {v}}|} ∀v→{\displaystyle \forall {\vec {v}}}