знак символ больше или равно, меньше или равно — Конреал
03:10 pm — знак символ больше или равно, меньше или равно
Замучился искать два знака, символа: больше или равно, меньше или равно.
Таки нашел: ≥ ≤ и много полезных других, прошу любить, жаловать и использовать по назначению.
Cимвол больше или равно, меньше или равно и др. специальные символы
Символ | ASCII-код / | Назначение |
Буквы и знаки препинания | ||
|   | Неразрывный пробел | |
| @ | @ | Коммерческое «эт» («собака») |
| & | & | Амперсенд |
| « | " | Простые кавычки |
| “ | “ | Открывающая кавычка («лапочка») |
| ” | ” | Закрывающая кавычка («лапочка») |
| « | « | Открывающая кавычка («елочка») |
| » | » | Закрывающая кавычка («елочка») |
| — | — | Длинное тире |
| – | – | Короткое тире |
| … | … | Многоточие |
| ¦ | ¦ | Вертикальная черта |
| ¤ | ¤ | «Солнышко» |
| § | § | Параграф (раздел) |
| ¶ | ¶ | Параграф |
Математические символы | ||
| < | &lt; | Знак «меньше» |
| > | &gt; | Знак «больше» |
| ≤ | &le; | Знак «меньше или равно» |
| ≥ | &ge; | Знак «больше или равно» |
| ≈ | &asymp; | Примерное равенство |
| ≠ | &ne; | Неравенство |
| ≡ | &equiv; | Тождество |
| − | &minus; | Знак минуса (аналог короткого тире) |
| × | &times; | Знак умножения |
| ÷ | &divide; | Знак деления |
| ± | &plusmn; | Плюс/минус |
| &not; | Логическое отрицание | |
| ¯ ‾ | &macr; &oline; | Надчеркивание (два варианта разной длины) |
| ° | &deg; | Градус |
| ƒ | &fnof; | Функция |
| ∑ | &sum; | Сумма |
| ∏ | &prod; | Произведение |
| ∫ | &int; | Интеграл |
| ∂ | &part; | Символ дифференциала |
| √ | &radic; | Знак радикала |
| ∞ | &infin; | Знак бесконечности |
| Ø | &Oslash; | Зачеркнутое «О» (в качестве «пустого множества») |
| ∩ | &cap; | Пересечение |
| µ | &micro; | Обозначение «10-6» (визуально отличается от греческой «мю») |
| ² ³ | &sup2; &sup3; | Квадрат и куб |
Греческие буквы | ||
| Α α | &Alpha; &alpha; | Альфа |
| Β β | &Beta; &beta; | Бета |
| Γ γ | &Gamma; &gamma; | Гамма |
| Δ δ | &Delta; &delta; | Дельта |
| Ε ε | &Epsilon; &epsilon; | Эпсилон |
| Ζ ζ | &Zeta; &zeta; | Дзета |
| &Eta; &eta; | Эта | |
| Θ θ | &Theta; &theta; | Тэта |
| Ι ι | &Iota; &iota; | Иота (йота) |
| Κ κ | &Kappa; &kappa; | Каппа |
| Λ λ | &Lambda; &lambda; | Лямбда (ламбда) |
| Μ μ | &Mu; &mu; | Мю (ми) |
| Ν ν | &Nu; &nu; | Ню (ни) |
| Ξ ξ | &Xi; &xi; | Кси |
| Ο ο | &Omicron; &omicron; | Омикрон |
| Π π | &Pi; &pi; | Пи |
| Ρ ρ | &Rho; &rho; | Ро |
| Σ σ | &Sigma; &sigma; | Сигма |
| Τ τ | &Tau; &tau; | Тау |
| Υ υ | &Upsilon; &upsilon; | Ипсилон |
| Φ φ | &Phi; &phi; | Фи |
| Χ χ | &Chi; &chi; | Хи |
| Ψ ψ | &Psi; &psi; | |
Неравенство — Википедия
Нера́венство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков[1].

Область допустимых решений («feasible region») в задачах линейного программирования
- Строгие неравенства
Неравенства a>b{\displaystyle a>b} и b<a{\displaystyle b<a} равносильны. Говорят, что знаки >{\displaystyle >} и <{\displaystyle <} противоположны; например, выражение «знак неравенства сменился на противоположный» означает, что <{\displaystyle <} заменено на >{\displaystyle >} или наоборот.
- Нестрогие неравенства
Русскоязычная традиция начертания знаков ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } отличается от принятой за рубежом, где обычно используются знаки ≤{\displaystyle \leq } и ≥{\displaystyle \geq }. Про знаки ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } также говорят, что они противоположны.
- Другие типы неравенств
Далее в данной статье, если не оговорено иное, понятие неравенства относится к первым 4 типам.
В элементарной математике изучают числовые неравенства. В общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы.
Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»).
Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:
- a<b<c{\displaystyle a<b<c} — это краткая запись пары неравенств: a<b{\displaystyle a<b} и b<c.{\displaystyle b<c.}
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных (x,y,…).{\displaystyle (x,y,\dots ).} Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство 18x<414{\displaystyle 18x<414} — алгебраическое первой степени, неравенство 2×3−7x+6>0{\displaystyle 2x^{3}-7x+6>0} — алгебраическое третьей степени, неравенство 2x>x+4{\displaystyle 2^{x}>x+4} — трансцендентное
Свойства[править | править код]
Свойства числовых неравенств в некоторых отношениях близки к свойствам уравнений[1]:
- К обеим частям неравенства можно прибавить одно и то же число.
- От обеих частей неравенства можно отнять одно и то же число. Следствие: как и для уравнений, любой член неравенства можно перенести в другую часть с противоположным знаком. Например, из a+b<c{\displaystyle a+b<c} следует, что a<c−b.{\displaystyle a<c-b.}
- Обе части неравенства можно умножить на одно и то же положительное число.
- Одноимённые неравенства можно складывать: если, например, a<b{\displaystyle a<b} и c<d,{\displaystyle c<d,} то a+c<b+d.{\displaystyle a+c<b+d.} Неравенства с противоположными знаками можно аналогично почленно вычитать.
- Если все четыре части двух неравенств положительны, то неравенства можно перемножить.
- Если обе части неравенства положительны, то их можно возвести в одну и ту же (натуральную) степень, а также логарифмировать с любым основанием (если основание логарифма меньше 1, то знак неравенства надо изменить на противоположный).
- Другие свойства
- (Транзитивность) Если a<b{\displaystyle a<b} и b<c,{\displaystyle b<c,} то a<c{\displaystyle a<c} и аналогично для прочих знаков.
- Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный: больше на меньше, больше или равно на меньше или равно и т. д.
Решение неравенств[править | править код]
Если неравенство содержит символы неизвестных, то решение его означает выяснение вопроса, при каких значениях неизвестных неравенство выполняется. Примеры:
- x2<4{\displaystyle x^{2}<4} выполняется при −2<x<2.{\displaystyle -2<x<2.}
- x2>4{\displaystyle x^{2}>4} выполняется, если либо x>2,{\displaystyle x>2,} либо x<−2.{\displaystyle x<-2.}
- x2<−4{\displaystyle x^{2}<-4} не выполняется никогда (решений нет).
- x2>−4{\displaystyle x^{2}>-4} выполняется при всех x{\displaystyle x} (тождество).
Внимание: если возвести в чётную степень неравенство, содержащее неизвестные, могут появиться «лишние» решения. Пример: если неравенство x>3{\displaystyle x>3} возвести в квадрат: x2>9,{\displaystyle x^{2}>9,} то появится ошибочное решение x<−3,{\displaystyle x<-3,} не удовлетворяющее исходному неравенству. Поэтому все полученные таким образом решения следует проверить подстановкой в исходное неравенство.
Неравенства первой степени[править | править код]
Неравенство первой степени имеет общий формат: ax>b{\displaystyle ax>b} или ax<b,{\displaystyle ax<b,} где a≠0{\displaystyle a\neq 0} (работа со знаками ⩾{\displaystyle \geqslant } и ⩽{\displaystyle \leqslant } аналогична). Чтобы его решить, разделите неравенство на a{\displaystyle a} и, если a<0,{\displaystyle a<0,} измените знак неравенства на противоположный[3]. Пример:
- 5x−11>8x+1.{\displaystyle 5x-11>8x+1.} Приведём подобные члены: −3x>12,{\displaystyle -3x>12,} или x<−4.{\displaystyle x<-4.}
Системы неравенств первой степени[править | править код]
Если одно и то же неизвестное входит более чем в одно неравенство, надо решить каждое неравенство в отдельности и затем сопоставить эти решения, которые должны выполняться все вместе.
Пример 1. Из системы {4x−3>5x−52x+4<8x{\displaystyle {\begin{cases}4x-3>5x-5\\2x+4<8x\end{cases}}} получаем два решения: для первого неравенства x<2,{\displaystyle x<2,} для второго: x>23.{\displaystyle x>{2 \over 3}.} Соединяя их, получаем ответ: 23<x<2.{\displaystyle {2 \over 3}<x<2.}
Пример 2. {2x−3>3x−52x+4>8x{\displaystyle {\begin{cases}2x-3>3x-5\\2x+4>8x\end{cases}}} Решения: x<2{\displaystyle x<2} и x<23.{\displaystyle x<{2 \over 3}.} Второе решение поглощает первое, так что ответ: x<23.{\displaystyle x<{2 \over 3}.}
Пример 3. {2x−3<3x−52x+4>8x{\displaystyle {\begin{cases}2x-3<3x-5\\2x+4>8x\end{cases}}} Решения: x>2{\displaystyle x>2} и x<23,{\displaystyle x<{2 \over 3},} они несовместимы, поэтому исходная система не имеет решений.
Неравенства второй степени[править | править код]
Общий вид неравенства второй степени (называемого также квадратным неравенством):
- x2+px+q>0{\displaystyle x^{2}+px+q>0} или x2+px+q<0.{\displaystyle x^{2}+px+q<0.}
Если квадратное уравнение x2+px+q=0{\displaystyle x^{2}+px+q=0} имеет вещественные корни x1,x2,{\displaystyle x_{1},x_{2},} то неравенство можно привести к виду соответственно:
- (x−x1)(x−x2)>0{\displaystyle (x-x_{1})(x-x_{2})>0} или (x−x1)(x−x2)<0.{\displaystyle (x-x_{1})(x-x_{2})<0.}
В первом случае x−x1{\displaystyle x-x_{1}} и x−x2{\displaystyle x-x_{2}} должны иметь одинаковые знаки, во втором — разные. Для окончательного ответа надо применить следующее простое правило[4].
Квадратный трёхчлен x2+px+q{\displaystyle x^{2}+px+q} с разными вещественными корнями отрицателен в интервале между корнями и положителен вне этого интервала. |
Если оказалось, что у уравнения x2+px+q=0{\displaystyle x^{2}+px+q=0} вещественных корней нет, то его левая часть сохраняет один и тот же знак при всех x.{\displaystyle x.} Поэтому исходное неравенство второй степени либо является тождеством, либо не имеет решений (см. ниже примеры[5]).
Пример 1. −2×2+14x−20>0.{\displaystyle -2x^{2}+14x-20>0.} Разделив на −2,{\displaystyle -2,} приведём неравенство к виду: x2−7x+10<0.{\displaystyle x^{2}-7x+10<0.} Решив квадратное уравнение x2−7x+10=0,{\displaystyle x^{2}-7x+10=0,} получаем корни x1=2;x2=5,{\displaystyle x_{1}=2;x_{2}=5,} поэтому исходное неравенство равносильно такому: (x−2)(x−5)<0.{\displaystyle (x-2)(x-5)<0.} Согласно приведенному выше правилу, 2<x<5,{\displaystyle 2<x<5,} что и является ответом.
Пример 2. −2×2+14x−20<0.{\displaystyle -2x^{2}+14x-20<0.} Аналогично получаем, что x−2{\displaystyle x-2} и x−5{\displaystyle x-5} имеют одинаковые знаки, то есть, согласно правилу, либо x<2,{\displaystyle x<2,} либо x>5.{\displaystyle x>5.}
Пример 3. x2+6x+15>0.{\displaystyle x^{2}+6x+15>0.} Уравнение x2+6x+15=0{\displaystyle x^{2}+6x+15=0} не имеет вещественных корней, поэтому левая часть его сохраняет знак при всех x.{\displaystyle x.} При x=0{\displaystyle x=0} левая часть положительна, поэтому исходное неравенство есть тождество (верно при всех x{\displaystyle x}).
Пример 4. x2+6x+15<0.{\displaystyle x^{2}+6x+15<0.} Как и в предыдущем примере, здесь левая часть всегда положительна, поэтому неравенство не имеет решений.
Аналогично, разложением на множители, можно решать неравенства высших степеней. Другой способ — построить график левой части и определить, какие знаки она имеет в различных интервалах[6].
Прочие неравенства[править | править код]
Существуют также дробно-рациональные, иррациональные, логарифмические и тригонометрические неравенства.
Ниже приведены практически полезные неравенства, тождественно выполняющиеся, если неизвестные попадают в указанные границы[7].
- (1+x)n⩾1+nx,{\displaystyle (1+x)^{n}\geqslant 1+nx,} где x⩾−1,n{\displaystyle x\geqslant -1,n} — натуральное число.
- |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|}
- См. следствия этого неравенства в статье Абсолютная величина.
Знаки неравенства в языках программирования[править | править код]
Символ «не равно» в разных языках программирования записывается по-разному.
| Символ | Языки |
|---|---|
| != | C, C++, C#, Java, JavaScript, Perl, PHP, Python, Wolfram Language |
| <> | Basic, Pascal |
| ~= | Lua |
| /= | Haskell, Fortran, Ada |
| # | Modula-2, Oberon |
Начертание символа «Знак меньше» в разных шрифтах
Описание символа
Знак меньше ставится для того, чтобы показать, что одно число (выражение, переменная) меньше другого. Этот математический оператор является одним из знаков неравенства. Неравенство в математике — утверждение об относительной величине двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В Юникоде, знак больше находится в разделе основная латиница с версии 1.0.0 от 1991 года.
Этот текст также доступен на следующих языках: Español;
Подробнее СкрытьПохожие символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | 3C | 60 | 60 | 00111100 |
| UTF-16BE | 00 3C | 0 60 | 60 | 00000000 00111100 |
| UTF-16LE | 3C 00 | 60 0 | 15360 | 00111100 00000000 |
| UTF-32BE | 00 00 00 3C | 0 0 0 60 | 60 | 00000000 00000000 00000000 00111100 |
| UTF-32LE | 3C 00 00 00 | 60 0 0 0 | 1006632960 | 00111100 00000000 00000000 00000000 |
Наборы с этим символом:
Символ | Название | Объяснение | Примеры | Значение Unicode | Название в HTML | Символ LaTeX |
|---|---|---|---|---|---|---|
| Читается как | ||||||
| Категория | ||||||
| Импликация | A ⇒ B верно, только когда либо A ложно, либо B истинно. → может означать то же самое, что и ⇒ (символ может также указывать область определения и область значений функции, см. таблицу математических символов). ⊃ может означать то же самое, что и ⇒ (символ может также обозначать надмножество). | x = 2 ⇒ x2 = 4 истинно, но x2 = 4 ⇒ x = 2, в общем случае, ложно (поскольку x может быть равен −2). | U+21D2 U+2192 U+2283 | ⇒ → ⊃ | ⇒{\displaystyle \Rightarrow }\Rightarrow →{\displaystyle \to }\to ⊃{\displaystyle \supset }\supset ⟹{\displaystyle \implies }\implies | |
| из .. следует; если .. то | ||||||
| логика высказываний, алгебра Гейтинга[en] | ||||||
| Тогда и только тогда | A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны. | x + 5 = y + 2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 | ⇔ ≡ ↔ | ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow ≡{\displaystyle \equiv }\equiv ↔{\displaystyle \leftrightarrow }\leftrightarrow ⟺{\displaystyle \iff }\iff | |
| тогда и только тогда | ||||||
| логика высказываний | ||||||
| отрицание | Утверждение ¬A истинно тогда и только тогда, когда A ложно. Знак /, расположенный поверх другого оператора, означает то же самое, что «¬», помещённое перед выражением. | ¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) | U+00AC U+02DC | ¬ ˜ ~ | ¬{\displaystyle \neg }\lnot или \neg ∼{\displaystyle \sim }\sim | |
| not (не) | ||||||
| логика высказываний | ||||||
| конъюнкция | Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае. | n < 4 ∧ n >2 ⇔ n = 3, если n — натуральное число. | U+2227 U+0026 | ∧ & | ∧{\displaystyle \wedge }\wedge или \land \&[2] | |
| and (и) | ||||||
| логика высказываний, Булева алгебра | ||||||
| логическая дизъюнкция | Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны, утверждение неверно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 когда n является натуральным числом. | U+2228 | ∨ | ∨{\displaystyle \lor }\lor или \vee | |
| or (или) | ||||||
| логика высказываний, Булева алгебра | ||||||
| исключающее или | Утверждение A ⊕ B верно, когда либо A, либо B верно, но не оба. A ⊻ B означает то же самое. | (¬A) ⊕ A всегда верно, A ⊕ A всегда неверно. | U+2295 U+22BB | ⊕ | ⊕{\displaystyle \oplus }\oplus ⊻{\displaystyle \veebar }\veebar | |
| xor | ||||||
| логика высказываний, Булева алгебра | ||||||
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | U+22A4 | T | ⊤{\displaystyle \top }\top | |
| верх | ||||||
| логика высказываний, Булева алгебра | ||||||
| Противоречие | Утверждение ⊥ безусловно неверно. | ⊥ ⇒ A всегда верно. | U+22A5 | ⊥ F | ⊥{\displaystyle \bot }\bot | |
| ложь, неверно, ошибочно | ||||||
| логика высказываний, Булева алгебра | ||||||
| Квантор всеобщности | ∀ x: P(x) или (x) P(x) означает P(x) верно для всех x. | ∀ n ∈ ℕ: n2 ≥ n. | U+2200 | ∀ | ∀{\displaystyle \forall }\forall | |
| для любого; для всех | ||||||
| Логика первого порядка | ||||||
∃ | Квантор существования | ∃ x: P(x) означает, что существует по меньшей мере один x, такой, что P(x) верно. | ∃ n ∈ ℕ: n чётно. | U+2203 | ∃ | ∃{\displaystyle \exists }\exists |
| существует | ||||||
| логика первого порядка | ||||||
∃! | Единственность | ∃! x: P(x) означает, что существует ровно один x, такой, что P(x) верно. | ∃! n ∈ ℕ: n + 5 = 2n. | U+2203 U+0021 | ∃ ! | ∃!{\displaystyle \exists !}\exists ! |
| существует в точности один | ||||||
| логика первого порядка | ||||||
| Определение | x := y илиx ≡ y означает, что x является другим обозначением для y (но заметьте, что ≡ может означать и другое, как, например, конгруэнтность). P :⇔ Q означает, что P логически эквивалентно Q. | cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) | U+2254 (U+003A U+003D) U+2261 U+003A U+229C | := : ≡ ⇔ | :={\displaystyle :=}:= ≡{\displaystyle \equiv }\equiv ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow | |
| определяется как | ||||||
| везде | ||||||
() | приоритетная группировка | Операции внутри скобок выполняются первыми. | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. | U+0028 U+0029 | () | ( ){\displaystyle (~)} () |
| скобки | ||||||
| везде | ||||||
⊢ | Выводимо[en] | x ⊢ y означает, что y выводимо из x (в некоторых формальных системах). | A → B ⊢ ¬B → ¬A | U+22A2 | ⊢ | ⊢{\displaystyle \vdash }\vdash |
| выводимо | ||||||
| логика высказываний, логика первого порядка | ||||||
⊨ | Модель[en] | x ⊨ y означает, что x семантически влечёт за собой y | A → B ⊨ ¬B → ¬A | U+22A8 | ⊨ | ⊨{\displaystyle \vDash }\vDash |
| влечёт | ||||||
| логика высказываний, логика первого порядка |
| ЗНАК | ЗНАЧЕНИЕ | ПРИМЕР |
| = | равно | 5 = 5 |
| ≠ | не равно | 7 ≠ 5 |
| ≈ | приблизительно | 3,57 ≈ 3,6 |
| >, | больше, меньше | 8 > 5 |
| ≥ | больше или равно | a ≥ b |
| ≤ | меньше или равно | c ≤ b |
| + | плюс | 6 + 4 = 10 |
| — | минус | 10 — 6 = 4 |
| * | умножение | 5 * 3 = 15 |
| : | деление | 15 : 3 = 5 |
| ! | факториал | 3! = 1*2*3 = 6 |
| ∑ | сумма | |
| ⋅ | Оператор точка | |
| ⋆ | Оператор звезда | |
| ⊙ | Оператор точка в круге | |
| ⊚ | Оператор круг в круге | |
| ⊛ | Оператор звездочка в круге | |
| − | Знак минус | |
| ± | Знак плюс-минус | |
| ∓ | Знак минус-плюс | |
| ∔ | Знак точка-плюс | |
| × | Знак умножения | |
| ÷ | Знак деления | |
| ∞ | Знак бесконечность | |
| ˔ | Знак перпендикулярно | |
| ∼ | Оператор тильды (подобно) | |
| ∽ | Знак обратная тильда | |
| ≁ | Знак не тильда | |
| ≂ | Знак минус тильда | |
| ≃ | Знак асимптотически равный | |
| ≄ | Знак асимптотически равный | |
| ≈ | Знак почти равный (приблизительно) | |
| ≉ | Знак почти не равный | |
| ≊ | Знак равный или почти равный | |
| ≋ | Тройная тильда | |
| ≌ | Знак все равны | |
| ≅ | Знак приблизительно равный | |
| ≆ | Знак фактически равный | |
| ≇ | Знак фактически не равный | |
| ≠ | Знак не равно | |
| > | Знак больше | |
| < | Знак меньше | |
| ≤ | Знак меньше или равно | |
| ≥ | Знак больше или равно | |
| ≦ | Меньше, чем над равно | |
| ≧ | Больше, чем над равно | |
| ≨ | Менее чем, но не равны | |
| ≩ | Больше чем, но не равны | |
| ≮ | Не меньше чем | |
| ≯ | Не больше чем | |
| ⋦ | Меньше чем, но не эквивалентны | |
| ⋧ | Больше чем, но не эквивалентны | |
| ⋖ | Меньше чем с точкой | |
| ⋗ | Больше чем с точкой | |
| ≰ | Ни меньше, ни равный | |
| ≱ | Ни больше, ни равный | |
| ⋜ | Равно или меньше чем | |
| ⋝ | Равно или больше чем | |
| ≲ | Меньше чем или эквивалентно | |
| ≳ | Больше чем или эквивалентно | |
| ≶ | Меньше чем или больше чем | |
| ≷ | Больше чем или меньше чем | |
| ≸ | Ни меньше чем, ни больше чем | |
| ≹ | Ни больше чем, ни меньше чем | |
| ⋚ | Меньше или равно или больше чем | |
| ⋛ | Больше или равно или меньше чем | |
| ≡ | Знак тождественно | |
| ≢ | Знак не идентично | |
| ≀ | Сплетение | |
| ≍ | Знак эквивалентно | |
| ≏ | Знак различие между | |
| ≣ | Строго эквивалентный | |
| ≪ | Гораздо меньше чем | |
| ≫ | Гораздо больше чем | |
| ⋘ | Много меньше чем | |
| ⋙ | Много больше чем | |
| ¬ | Знак отрицания (скобка) | |
| ∀ | Для всех | |
| ∂ | Частичный дифференциал | |
| ∃ | Существует | |
| ∄ | Не существует | |
| ∆ | Инкремент | |
| ∇ | Оператор набла | |
| ∈ | Элемент из | |
| ∉ | Не элемент из | |
| ∋ | Содержит в качестве члена | |
| ∌ | Не содержит как член | |
| √ | Квадратный корень | |
| ∛ | Кубический корень | |
| ∜ | Четвертый корень | |
| ∝ | Знак пропорционально | |
| ∠ | Знак угол | |
| ∟ | Прямой угол | |
| ⊾ | Прямой угол с дугой | |
| ∡ | Измеренный угол | |
| ∣ | Разделять | |
| ∤ | Не разделять | |
| ∥ | Параллельно | |
| ∦ | Не параллельно | |
| ∧ | Логическое «И» | |
| ∨ | Логическое «Или» | |
| ∩ | Пересечение | |
| ∪ | Союз (объединение) | |
| ∫ | Интеграл | |
| ∬ | Двойной интеграл | |
| ∭ | Тройной интеграл | |
| ∮ | Контурный интеграл | |
| ∯ | Поверхностный интеграл | |
| ∴ | Следовательно | |
| ∵ | Поскольку | |
| ∶ | Соотношение | |
| ∷ | Пропорция | |
| ∸ | Точка минус | |
| ∹ | Избыток | |
| ∺ | Геометрическая прогрессия | |
| ⊂ | Подмножество | |
| ⊃ | Супермножество | |
| ′ | Штрих | |
| ″ | Двойной штрих | |
| ‴ | Тройной штрих | |
| ½ | Одна вторая | |
| ℃ | Знак градуса по Цельсию | |
| N | натуральные числа | 1,2,3,4,5…. |
| Z | целые числа | -1,0,+1,+2 |
| R | рациональные числа |
Знак (математика) — Википедия
- Это статья о понятии положительности и отрицательности. О математических символах см. таблицу математических символов. О других значениях термина см. Знак.

Знак вещественного числа в арифметике позволяет отличить отрицательные числа от положительных; традиционно знак обозначается символом плюса (положительные числа) или минуса (отрицательные) перед записью числа. Если ни плюс, ни минус не указаны, число считается положительным. Ноль как особое число не имеет знака.
Примеры записи чисел: +36,6; −273; 142.{\displaystyle +36{,}6;\ {-}273;\ 142.} Последнее число не имеет знака и поэтому положительно.
Следует отметить, что плюс и минус указывают знак для чисел, но не для буквенных переменных или алгебраических выражений. Например, в формулах −t; a+b; −(a2+b2){\displaystyle -t;\ a+b;\ -(a^{2}+b^{2})} символы плюса и минуса задают не знак выражения, перед которым они стоят, а знак арифметической операции, так что знак результата может быть любым, он определяется только после вычисления выражения.
Кроме арифметики, понятие знака используется в других разделах математики, в том числе для нечисловых математических объектов (см. ниже). Понятие знака важно также в тех разделах физики, где физические величины делятся на два класса, условно названные положительными и отрицательными — например, электрические заряды, положительная и отрицательная обратная связь, разнообразные силы притяжения и отталкивания.
Положительные и отрицательные числа[править | править код]

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус[1].
Нулю не присвоен никакой знак, то есть +0{\displaystyle +0} и −0{\displaystyle -0} — это в арифметике одно и то же число[1]. В математическом анализе смысл символов +0{\displaystyle +0} и −0{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.
В связи со сказанным вводятся ещё несколько полезных терминов:
- Число неотрицательно, если оно больше или равно нулю.
- Число неположительно, если оно меньше или равно нулю.
- Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.
Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..
Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.
Функция знака sgn(x)[править | править код]
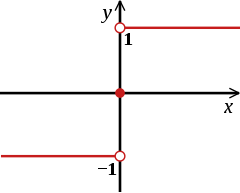 График функции y=sgn(x){\displaystyle y=\operatorname {sgn}(x)}
Основная статья: sgn
График функции y=sgn(x){\displaystyle y=\operatorname {sgn}(x)}
Основная статья: sgnФункция знака y=sgn(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:
- sgn(x)={−1(x<0), 0(x=0), 1(x>0).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}
Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.
Пример использования функции см. в статье Квадратный корень#Комплексные числа.
Модуль (абсолютная величина) числа[править | править код]
Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}
Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.
Знак угла[править | править код]
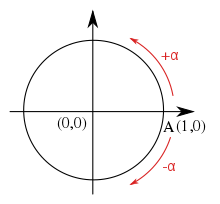 Положительные и отрицательные углы
Положительные и отрицательные углыВеличина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:
- вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
- поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.
Знак направления[править | править код]
В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.
Знак в вычислительной технике[править | править код]
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Для представления знака целого числа большинство компьютеров используют дополнительный код. | |||||||||
Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.
Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.
Дискретная математика[править | править код]
В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.
В теории графов рассматриваются ориентированные и знаковые графы[en], в которых каждому ребру соответствует направление или знак (положительный или отрицательный).
Другие применения знака[править | править код]
Существует знако-разрядная система счисления[en], в ней каждая цифра числа может иметь положительный или отрицательный знак..
В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.
Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.
В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона.
Как поставить знак больше/меньше или равно в Word с клавиатуры — 3 способа

Для печати знака сравнения «больше или равно» в Ворде достаточно запомнить несколько простых комбинаций клавиш или воспользоваться одним секретным приёмом. Аналогичные способы будут рассмотрены и для символа «меньше или равно».
XY ≥ 15 = Great
Способы печати «больше или равно»
Рассмотрим 3 лучших способа вставки.
Alt код
У каждого символа есть цифровой код, который в Ворде можно преобразовать в сам знак. Для этого в любом месте документа печатаем «2265» и затем одновременно на клавиатуре нажимаем Alt и X.

Секретный приём
Секретный приём можно использовать в любом текстовом редакторе. Если напечатать обычный знак больше, а затем сделать его подчеркнутым (Ctrl + U), то по написанию он будет выглядеть в точности как нужный символ.
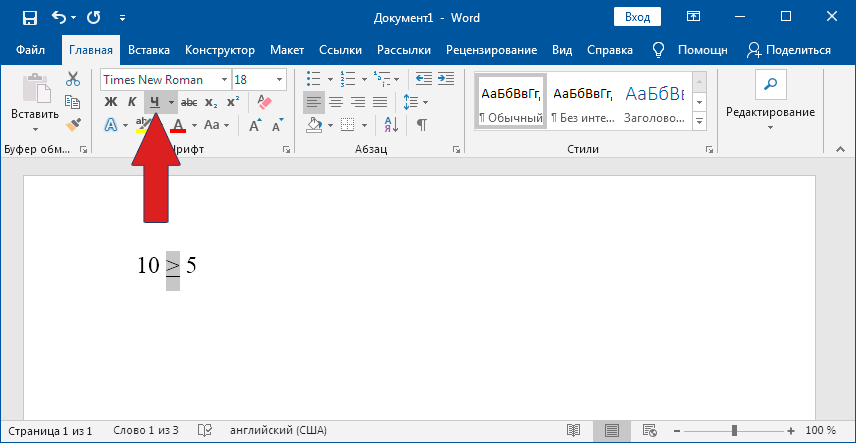
Использовать на практике такой подход рекомендую в крайних случаях, когда по-другому не получается.
Вставка в формуле
Рассматриваемые знаки являются математическими и чаще всего применяются в формулах. Для вставки формулы в Word применяют горячие клавиши Alt и =. При этом создается специальное поле для ввода математического выражения.
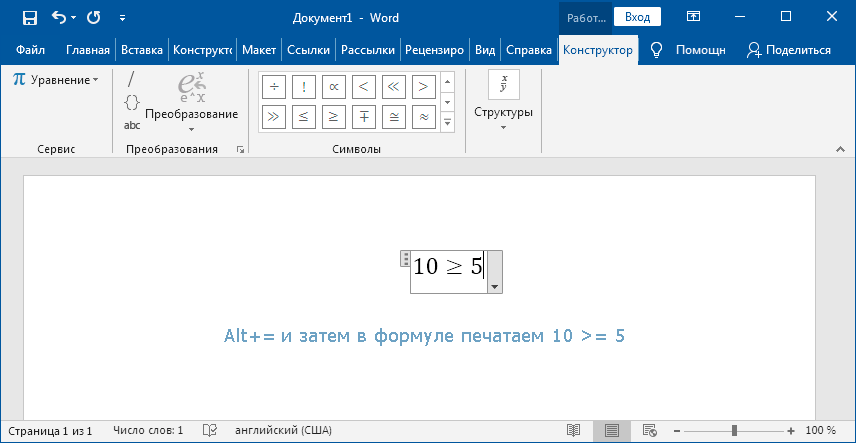
Чтобы в этом поле напечатать «больше или равно», достаточно ввести последовательно >= и нажать пробел. Два символа автоматически заменяться на нужный знак.
Вставляем «меньше или равно»
Знак «меньше или равно» вставляется как в предыдущих примерах, с небольшими изменениями. В первом случае меняется только код на «2264».
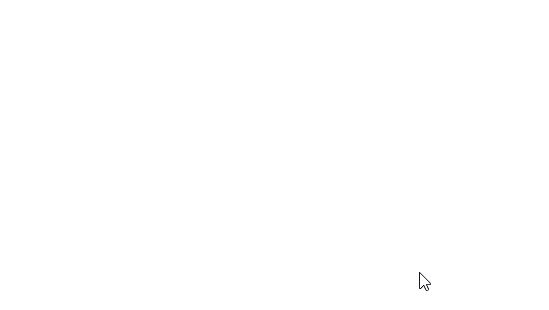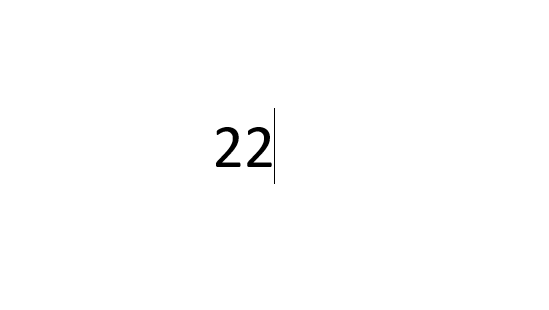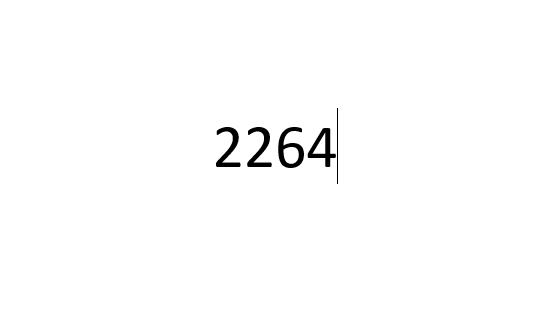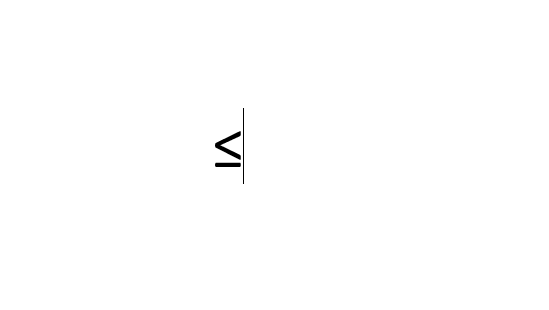
В примере с форумлами последовательность заменяется на .
Andy Si
29 окт. 2019 г.
839
