Ст. 46 ч. 1 п. 4 – для должника означает приостановление
В России с каждым годом растет число должников по кредитам, так как кредиты в нашей стране сегодня это просто национальная игра, как правило – азартная и берут их все, кому не лень, в том числе те, кто возвратить деньги не сможет. Естественно, взяв кредит, и не отдав его вовремя гражданин превращается в должника, в отношении него выносится судебный приказ или решение, дело передается судебным приставам и возбуждается исполнительное производство.
Точно такая же история происходит и по другим не кредитным судебным взысканиям, например, по алиментам. По окончании суда за дело всегда берутся судебные приставы, которые в рамках исполнительного производства взыскивают или пытаются взыскать деньги у должника.
А что бывает, если денег у должника просто нет. Исполнительное производство длится вечно? Нет, в этом случае судебным приставом применяется статья 46 часть 1 пункт 4. Вот об этой статье сегодня и будет наш разговор.
В сети интернет можно увидеть много публикаций, посвященных ст46 ч1 п4. Эта тема очень популярна у россиян и по этой причине сайты пытаются привлечь читателей на свои страницы публикациями на эту злободневную тему.
Большинство статей в интернете, рассказывающих о том, что значит для должника ст.46 ч.1 п.4 исполнительного производства написаны не юристами, а просто фрилансерами, часто не осознающими то, о чем они пишут. Такие статьи легко отличить по большому количеству содержащихся в них фотографий и рекламных блоков. Точность информации на таких страницах конечно же далека от истины.
Данная статья написана юристом с опытом 10 лет работы в Службе судебных приставов Одинцовского городского округа Московской области и последующим опытом работы юристом, в том числе по юридическому сопровождению исполнительного производства.
Так как основными читателями сайта являются люди без юридического образования, я постараюсь без излишних юридических терминов, простыми словами рассказать о том, что означает для должника ст 46 ч 1 п 4 в исполнительном производстве, можно ли в этом случае, например, выехать за рубеж, продать автомобиль, снимется ли арест с банковского счета и т. д.
д.
В своей работе судебные приставы используют закон, который определяет порядок их работы с должниками. Этот закон наделяет пристава полномочиями получать информацию о должнике, его имуществе и доходах, арестовывать его имущество и выставлять его на торги.
Очень часто, а в последнее время практически всегда – судебный пристав не имеет возможности полностью или в части исполнить решение суда по причине того, что у должника не хватает или полностью нет денег и имущества. Возможно, у таких людей всё же имеется неофициальный доход, имущество записано на родственников и друзей, но официально они чисты и у самого должника очень часто официально нет ничего.
В этом случае судебный пристав, вопреки желанию взыскателя, может прекратить работу по взысканию долга на основании ст. 46 ч. 1 п. 4. Однако, применяется такое послабление только на определенное время, и об этом мы поговорим ниже.
Когда приостанавливается исполнительное производство
- Первый случай применения ст.
 46 ч. 1 п. 4, это когда к судебному приставу поступил исполнительный лист на взыскание денег, но, после проведения работы по установлению материального положения должника выясняется, что доходов, имущества и денег у него нет.
46 ч. 1 п. 4, это когда к судебному приставу поступил исполнительный лист на взыскание денег, но, после проведения работы по установлению материального положения должника выясняется, что доходов, имущества и денег у него нет. - Второй случай применения такой статьи закона – судебному приставу удалось частично исполнить решение суда, долг частично погашен, но вдруг выяснилось, что денег больше нет, материальное положение гражданина ухудшилось и перспективы дальнейшего взыскания утрачены.
- Третий случай тоже нельзя исключать — это нежелание судебного пристава добросовестно исполнять свою работу, делать запросы по розыску имущества и денег, выезжать по месту жительства должника. Что делать в такой ситуации? В этом случае исполнительное производство, прекращенное по ст. 46 ч. 1 п. 4 целесообразно возобновить, обжаловав бездействие пристава в суде. А это значит у Вас есть все шансы продолжить взыскание без нежелательного перерыва.
6 месяцев — срок приостановления
Итак, судебный пристав приостановил исполнительное производство, применив статья 46 часть 1 пункт 4. Что это означает для должника? Прощение долга происходит навсегда?
Что это означает для должника? Прощение долга происходит навсегда?
Нет, закон дает только лишь небольшую передышку должнику, для того, чтобы он мог поправить свое материальное положение, приобрести имущество, устроиться на работу.
Такая передышка дается на 6 месяцев. Именно такой срок предусмотрен данной статьей и это значит, что по истечении 6 месяцев должником снова заинтересуется судебный пристав.
Но для этого, взыскателю надо вновь обратиться к судебному приставу с исполнительным листом, не пропустив при этом срок в 3 года с даты приостановки производства по делу.
Что дает должнику приостановление взыскания по статье 46 части 1 пункту 4
- Если производство приостановлено, но пристав уже успел что-то арестовать, например, автомобиль или недвижимое имущество – арест снят не будет.
- Если у Вас был наложен запрет на выезд заграницу – теперь Вы свободны и можете ехать, лететь куда угодно.
- Если у Вас арестован счет, на котором нет денег – счет будет разблокирован, но деньги на него лучше, конечно же не перечислять, так как по истечении 6 месяцев счет будет снова арестован.

- Если Вы объявлены в розыск, после применения к Вам ст.46 ч.1 п.4, розыск будет снят и Вы можете спокойно передвигаться по стране.
- Если у Вас нет работы, дохода, но появилась возможность трудоустроиться – начав работать и получать доход 6 месяцев Вас никто не будет беспокоить и интересоваться Вашими деньгами.
- Применение ст. 46 ч. 1 п. 4 вовсе не означает, что у гражданина теперь чистая кредитная история. Долг считается не погашенным, банки будут иметь такие сведения и с получением кредитов конечно же будут трудности.
- Если у Вас долг по алиментам, то невозможность взыскать его через службу судебных приставов не лишает права второго родителя на возбуждение уголовного дела по факту злостного уклонения от уплаты алиментов.
Юрист Сергей Синицын (Московская область)
Адвокат рассказывает про то, как платить приставу меньше 50% и в каких случаях можно ограничиться 10% ежемесячного удержания с зарплаты или пенсии :
Подписавшись на Ютуб-канал, в комментариях к видео можно отставить свой вопрос, и адвокат быстро ответит на него своим подписчикам!
Статьи на интересные темы:
- Уголок потребителя – зачем он нужен в любом бизнесе и какие штрафы если его нет.
 °-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
\(sin\) \(a\) \(→\) \(cos\) \(a\)
\(cos\) \(a\) \(→\) \(sin\) \(a\)
\(tg\) \(a\) \(→\) \(ctg\) \(a\)
\(ctg\) \(a\) \(→\) \(tg\) \(a\)Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс, он либо останется синусом, либо превратиться в косинус.
 °}}=\)
°}}=\)
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
\(= 18\)
Записываем ответ
Ответ: \(18\)
Пример. Найдите значение выражения \(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}\)
Решение:
\(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\)
Рассмотрим первое слагаемое числителя: \(\sin(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно: - \((π-a)\) это вторая четверть, а синус во второй четверти положителен.
 Значит, знак будет плюс;
Значит, знак будет плюс; - \(π\) это точка «горизонтальная», то есть мотаем головой, значит функция остается той же.
Таким образом, \(\sin(π-a)=\sina\)
\(=\frac{3 \sin{a}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\)
Второе слагаемое числителя: \(\cos{(\frac{π}{2} + a)}\): - \((\frac{π}{2} + a)\) это опять вторая четверть, а косинус во второй четверти отрицателен. Значит, знак будет минус.
- \(\frac{π}{2}\) это точка «вертикальная», то есть киваем, значит, функция меняется на кофункцию – синус.
Таким образом, \(\cos{(\frac{π}{2} + a)}=-\sina\)
\(=\frac{3 \sin{a}-(-\sin{a}) }{\cos {(\frac{3\pi}{2}-a)}}=\)
Теперь знаменатель: \(\cos(\frac{3π}{2} — a)\).
 Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\)
Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\)\(=\frac{3 \sin{a}-(-\sin{a}) }{-\sin {a}}=\)
Раскрываем скобки и приводим подобные слагаемые.
\(=\frac{3 \sin{a}+\sin{a}}{-\sin {a}}=\frac{4\sin{a}}{-\sin{a}}\)
Сократив на \(\sin{a}\), получаем ответ.
\(=\frac{4 }{-1}=\)\(-4\)
Ответ: \(-4\)
Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(a=2\)
Решение:
\(ctg(-a-\frac{7π}{2}) =\)
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный.
 Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.
Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.\(= ctg(-\frac{7π}{2}-a) =\)
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.
\(= ctg(-(\frac{7π}{2}+a)) =\)
Теперь вспомним о том, что котангенс – функция нечетная, то есть
\(ctg\) \((-t)=- ctg\) \(t\). Преобразовываем наше выражение.\(= — ctg(\frac{7π}{2}+a) =\)
Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже).
 \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
\((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
\(= — (- tg\) \(a) = tg\) \(a = 2\)
Готов ответ.
Ответ: \(2\)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:
\(cos\) \(t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…\)
\(sin\) \(t=sin (t+2π)=sin (t+4π)=sin (t+6π)= . ..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).
\(tg\) \(t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…\)
\(ctg\) \(t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…\)Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Смотрите также Как доказать тригонометрическое тождество?
ЗАКОНОДАТЕЛЬНЫЙ ПРОЦЕСС | Совет Федерации Федерального Собрания Российской Федерации
ЗАКОНОДАТЕЛЬНЫЙ ПРОЦЕСС
Урегулированная правовыми нормами деятельность уполномоченных органов государственной власти и должностных лиц по созданию закона. В РФ З. п. регулируется Конституцией РФ, регламентами и иными актами палат ФС РФ, нормативными актами Президента РФ, Правительства РФ, принятыми в пределах их компетенции. Конституция РФ определила три главных участника З. п. Ими являются Президент РФ, СФ и ГД. Все они участвуют в З. п. лишь в той мере, в какой это предписано Конституцией РФ (ч. 1, 3 и 4 ст. 105, ст. 106, ч. 2 ст. 107, ст. 108).
З. п. состоит из пяти основных стадий.
Первая стадия З. п. – внесение законопроекта в ГД. В соответствии со ст.
 104 Конституции РФ законопроекты вносятся в ГД субъектами права законодательной инициативы: Президентом РФ, СФ, сенаторами РФ, депутатами ГД, Правительством РФ, законодательными (представительными) органами государственной власти субъектов РФ. Право законодательной инициативы принадлежит также Конституционному Суду РФ, Верховному Суду РФ по вопросам их ведения. Законопроекты о введении или отмене налогов, освобождении от их уплаты, о выпуске государственных займов, об изменении финансовых обязательств государства, др. законопроекты, предусматривающие расходы, покрываемые за счет федерального бюджета, могут быть внесены только при наличии заключения Правительства РФ.
104 Конституции РФ законопроекты вносятся в ГД субъектами права законодательной инициативы: Президентом РФ, СФ, сенаторами РФ, депутатами ГД, Правительством РФ, законодательными (представительными) органами государственной власти субъектов РФ. Право законодательной инициативы принадлежит также Конституционному Суду РФ, Верховному Суду РФ по вопросам их ведения. Законопроекты о введении или отмене налогов, освобождении от их уплаты, о выпуске государственных займов, об изменении финансовых обязательств государства, др. законопроекты, предусматривающие расходы, покрываемые за счет федерального бюджета, могут быть внесены только при наличии заключения Правительства РФ.Вторая стадия З. п. – рассмотрение законопроекта ГД. Рассмотрение законопроектов ГД осуществляется, как правило, в трех чтениях. По результатам рассмотрения ГД может принять следующие решения: одобрить законопроект в качестве федерального конституционного закона, принять законопроект в качестве федерального закона, отклонить законопроект.
 Одобренные ГД федеральные конституционные законы и принятые ГД федеральные законы в обязательном порядке в течение 5 дней передаются на рассмотрение СФ.
Одобренные ГД федеральные конституционные законы и принятые ГД федеральные законы в обязательном порядке в течение 5 дней передаются на рассмотрение СФ.На третьей стадии З. п. одобренный ГД федеральный конституционный закон, принятый ГД федеральный закон рассматривает СФ. Федеральный конституционный закон считается принятым, если он одобрен большинством не менее трех четвертей голосов от общего числа сенаторов РФ и не менее двух третей голосов от общего числа депутатов ГД. После одобрения СФ федерального конституционного закона он считается принятым и подлежит подписанию Президентом РФ. Федеральные законы одобряются СФ. Если СФ в предусмотренный Конституцией РФ 14-дневный срок не рассмотрел принятый ГД федеральный закон на заседании палаты, он в соответствии с ч. 4 ст. 105 Конституции РФ считается одобренным СФ и направляется Президенту РФ для подписания и обнародования. Исключение из общего правила составляют федеральные законы, подлежащие обязательному рассмотрению СФ в соответствии со ст.
 106 Конституции РФ. Их рассмотрение в СФ с учетом п. 1 Постановления Конституционного Суда РФ от 23 марта 1995 «По делу о толковании части 4 статьи 105 и статьи 106 Конституции Российской Федерации» должно начаться не позднее 14 дней после их передачи в СФ. Палата имеет право отклонить федеральный конституционный закон, федеральный закон.
106 Конституции РФ. Их рассмотрение в СФ с учетом п. 1 Постановления Конституционного Суда РФ от 23 марта 1995 «По делу о толковании части 4 статьи 105 и статьи 106 Конституции Российской Федерации» должно начаться не позднее 14 дней после их передачи в СФ. Палата имеет право отклонить федеральный конституционный закон, федеральный закон.Четвертая стадия З. п. – подписание Президентом РФ принятых федерального конституционного закона и федерального закона – осуществляется в соответствии с Конституцией РФ. Ст. 107 Конституции РФ предусматривает, что принятый ГД и одобренный СФ федеральный закон в течение 5 дней направляется Президенту РФ для подписания и обнародования. В течение 14 дней он подписывает федеральный закон и обнародует его.
Согласно ч. 3 ст. 107 Конституции РФ если Президент РФ в течение четырнадцати дней с момента поступления федерального закона отклонит его, то ГД и СФ в установленном Конституцией РФ порядке вновь рассматривают данный закон. Если при повторном рассмотрении федеральный закон будет одобрен в ранее принятой редакции большинством не менее двух третей голосов от общего числа сенаторов РФ и депутатов ГД, он подлежит подписанию Президентом РФ в течение семи дней и обнародованию.
 Если Президент РФ в течение указанного срока обратится в Конституционный Суд РФ с запросом о проверке конституционности федерального закона, срок для подписания такого закона приостанавливается на время рассмотрения запроса Конституционным Судом РФ. Если Конституционный Суд РФ подтвердит конституционность федерального закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального закона, Президент РФ возвращает его в ГД без подписания.
Если Президент РФ в течение указанного срока обратится в Конституционный Суд РФ с запросом о проверке конституционности федерального закона, срок для подписания такого закона приостанавливается на время рассмотрения запроса Конституционным Судом РФ. Если Конституционный Суд РФ подтвердит конституционность федерального закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального закона, Президент РФ возвращает его в ГД без подписания.В соответствии с ч. 2 ст. 108 Конституции РФ принятый федеральный конституционный закон в течение четырнадцати дней подлежит подписанию Президентом Российской Федерации и обнародованию. Если Президент Российской Федерации в течение указанного срока обратится в Конституционный Суд РФ с запросом о проверке конституционности федерального конституционного закона, срок для подписания такого закона приостанавливается на время рассмотрения запроса Конституционным Судом РФ.
 Если Конституционный Суд РФ подтвердит конституционность федерального конституционного закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального конституционного закона, Президент РФ возвращает его в ГД без подписания.
Если Конституционный Суд РФ подтвердит конституционность федерального конституционного закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального конституционного закона, Президент РФ возвращает его в ГД без подписания.Официальное опубликование и вступление в силу федерального конституционного закона, федерального закона, подписанных Президентом РФ, является пятой стадией З. п. После подписания Президентом РФ законы должны быть обнародованы в порядке, установленном Федеральным законом от 14 июня 1994 «О порядке опубликования и вступления в силу федеральных конституционных законов, федеральных законов, актов палат Федерального Собрания». Официальным опубликованием федерального конституционного закона, федерального закона считается первая публикация его текста в «Парламентской газете», «Российской газете», «Собрании законодательства Российской Федерации» или первое размещение (опубликование) на «Официальном Интернет-портале правовой информации» (www.
 pravo.gov.ru). Подписанный Президентом РФ закон может быть опубликован также в др. печатных изданиях, обнародован по телевидению, радио, передан по каналам связи. Федеральные конституционные законы, федеральные законы вступают в силу одновременно на всей территории РФ по истечении 10 дней после дня их официального опубликования, если самими законами не установлен др. порядок вступления их в силу.
pravo.gov.ru). Подписанный Президентом РФ закон может быть опубликован также в др. печатных изданиях, обнародован по телевидению, радио, передан по каналам связи. Федеральные конституционные законы, федеральные законы вступают в силу одновременно на всей территории РФ по истечении 10 дней после дня их официального опубликования, если самими законами не установлен др. порядок вступления их в силу.Дополнительные стадии З. п. связаны с рассмотрением отклоненных СФ федерального конституционного закона, федерального закона и отклоненного федерального закона Президентом РФ. В случае отклонения СФ федерального закона ГД может принять одно из следующих решений: снять федеральный закон с дальнейшего рассмотрения в связи с отклонением его СФ; создать согласительную комиссию для преодоления возникших разногласий; принять федеральный закон в ранее принятой ГД редакции. Согласительная комиссия может создаваться как по инициативе СФ, поддержанной ГД, так и по инициативе ГД, поддержанной СФ. Согласительная комиссия создается на паритетных началах из представителей СФ и ГД и рассматривает лишь те положения федерального конституционного закона, федерального закона, по которым возникли разногласия между СФ и ГД.
 Одобренный ГД федеральный конституционный закон, принятый ГД федеральный закон в редакции согласительной комиссии в течение 5 дней направляются на рассмотрение СФ. Если при повторном рассмотрении федерального закона, отклоненного СФ, ГД не приняла его в редакции согласительной комиссии или выразила свое несогласие с решением СФ об отклонении федерального закона, он ставится на голосование в ранее принятой редакции. Решение о принятии федерального закона в ранее принятой редакции принимается большинством не менее двух третей голосов от общего числа депутатов ГД. Принятый ГД федеральный закон в течение 5 дней направляется Президенту РФ для подписания и обнародования. Если решение о принятии федерального закона, отклоненного СФ, в ранее принятой ГД редакции не набрало необходимого для принятия числа голосов, то федеральный закон считается отклоненным и дальнейшему рассмотрению не подлежит. Особенностью рассмотрения федеральных законов, отклоненных Президентом РФ, является возможность создания ГД по предложению Президента РФ либо по согласованию с ним специальной комиссии для преодоления возникших разногласий с предложением СФ направить своих представителей для работы в такой комиссии.
Одобренный ГД федеральный конституционный закон, принятый ГД федеральный закон в редакции согласительной комиссии в течение 5 дней направляются на рассмотрение СФ. Если при повторном рассмотрении федерального закона, отклоненного СФ, ГД не приняла его в редакции согласительной комиссии или выразила свое несогласие с решением СФ об отклонении федерального закона, он ставится на голосование в ранее принятой редакции. Решение о принятии федерального закона в ранее принятой редакции принимается большинством не менее двух третей голосов от общего числа депутатов ГД. Принятый ГД федеральный закон в течение 5 дней направляется Президенту РФ для подписания и обнародования. Если решение о принятии федерального закона, отклоненного СФ, в ранее принятой ГД редакции не набрало необходимого для принятия числа голосов, то федеральный закон считается отклоненным и дальнейшему рассмотрению не подлежит. Особенностью рассмотрения федеральных законов, отклоненных Президентом РФ, является возможность создания ГД по предложению Президента РФ либо по согласованию с ним специальной комиссии для преодоления возникших разногласий с предложением СФ направить своих представителей для работы в такой комиссии. По окончании работы специальная комиссия представляет на повторное рассмотрение ГД федеральный закон в согласованной редакции. Если при повторном рассмотрении ГД федерального закона, отклоненного Президентом РФ, он принят в новой редакции, порядок его рассмотрения в СФ определен как вновь принятого. Если при повторном рассмотрении федеральный закон будет одобрен в ранее принятой редакции большинством не менее двух третей голосов от общего числа сенаторов РФ и депутатов ГД, он подлежит подписанию Президентом РФ в течение 7 дней и обнародованию.
По окончании работы специальная комиссия представляет на повторное рассмотрение ГД федеральный закон в согласованной редакции. Если при повторном рассмотрении ГД федерального закона, отклоненного Президентом РФ, он принят в новой редакции, порядок его рассмотрения в СФ определен как вновь принятого. Если при повторном рассмотрении федеральный закон будет одобрен в ранее принятой редакции большинством не менее двух третей голосов от общего числа сенаторов РФ и депутатов ГД, он подлежит подписанию Президентом РФ в течение 7 дней и обнародованию.Таким образом, число стадий З. п. может изменяться (варьироваться) в зависимости от характера принимаемого закона и позиции по нему каждой из палат ФС РФ и Президента РФ.
Квантовые числа для атомов — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- \((π-a)\) это вторая четверть, а синус во второй четверти положителен.
- Идентификатор страницы
- 1709
- Ответить
Излучение, потому что энергия теряется при испускании фотона.

- Ответить
Поскольку \(l\) может быть нулем или целым положительным числом меньше (\(n-1\)), оно может принимать значения 0, 1, 2, 3, 4, 5 или 6.

- Ответить
Количество угловых узлов равно значению l , поэтому количество узлов также равно 4.
- Ответить
Поскольку \(m_l\) должен находиться в диапазоне от \(–l\) до \(+l\), тогда \(m_l\) может быть: -2, -1, 0, 1 или 2.

- Ответить
Четвертое квантовое число не зависит от первых трех, что позволяет совпадать первым трем квантовым числам двух электронов.
 Так как спин может быть +1/2 или =1/2, есть две комбинации:
Так как спин может быть +1/2 или =1/2, есть две комбинации:- \(n=2\), \(l=1\), \(m_l =0\), \(m_s=+1/2\)
- \(n=2\), \(l=1\), \(m_l=0\), \(m_s=-1/2\)
- Ответить
Нет, если значение \(m_s\) положительное, электрон «раскручивается».
- Ответить
Орбиталь с n=2, потому что чем ближе электрон к ядру или чем меньше атомный радиус, тем больше энергии требуется, чтобы вытолкнуть электрон.
- Когда n = 1, l = 0 (l принимает одно значение и, таким образом подоболочка может быть только одна)
- Когда n = 2, l = 0, 1 (l принимает два значения и, таким образом, возможны две подоболочки)
- Когда n = 3, l = 0, 1, 2 (l принимает три значения и, следовательно, существует три возможных подоболочки)
- Основная оболочка с n = 1 имеет одну подоболочку
- Основная оболочка с n = 2 имеет две подоболочки
- Основная оболочка с n = 3 имеет три подоболочки
- Главная оболочка с n = 1 имеет одну s подоболочку (l = 0)
- Основная оболочка с n = 2 имеет одну подоболочку s и одну подоболочку p (l = 0, 1)
- Основная оболочка с n = 3 имеет одну подоболочку s, одну подоболочку p и одну подоболочку d (l = 0, 1, 2)
- Ответить
Зная, что главное квантовое число n равно 4, и используя приведенную выше таблицу, мы можем заключить, что оно равно 4p.
- Ответить
3s, 3p и 3d. Поскольку n=3, возможные значения l = 0, 1, 2, что указывает на формы каждой подоболочки.
- Принцип исключения Паули: В 1926 году Вольфганг Паули обнаружил, что набор квантовых чисел специфичен для определенного электрона. То есть никакие два электрона не могут иметь одинаковые значения n, l, ml и ms. Хотя первые три квантовых числа определяют конкретную орбиталь и могут иметь одинаковые значения, четвертое имеет значение и должно иметь противоположные спины.
- Правило Хунда: орбитали могут иметь одинаковые энергетические уровни, если они находятся в одной и той же основной оболочке. Эти орбитали называются вырожденными или «равноэнергетическими». Согласно правилу Хунда, электроны заполняют орбитали по одному.
 Это означает, что при рисовании электронных конфигураций с помощью модели со стрелками вы должны заполнить каждую оболочку одним электроном, прежде чем начинать их спаривание. Помните, что заряд электрона отрицательный и электроны отталкиваются друг от друга. Электроны будут пытаться создать расстояние между ним и другими электронами, оставаясь неспаренными. Это также объясняет, почему спины электронов на орбитали противоположны (то есть +1/2 и -1/2).
Это означает, что при рисовании электронных конфигураций с помощью модели со стрелками вы должны заполнить каждую оболочку одним электроном, прежде чем начинать их спаривание. Помните, что заряд электрона отрицательный и электроны отталкиваются друг от друга. Электроны будут пытаться создать расстояние между ним и другими электронами, оставаясь неспаренными. Это также объясняет, почему спины электронов на орбитали противоположны (то есть +1/2 и -1/2). - Принцип неопределенности Гейзенберга: Согласно принципу неопределенности Гейзенберга, мы не можем одновременно точно измерить импульс и положение электрона. По мере того, как импульс электрона становится все более и более определенным, положение электрона становится менее определенным, и наоборот. Это помогает объяснить целые квантовые числа и почему n=2,5 не может существовать как главное квантовое число. Должно быть целое число длин волн (n), чтобы электрон мог поддерживать стоячую волну. Если бы существовали парциальные волны, то целые волны и парциальные волны компенсировали бы друг друга, и частица не двигалась бы.
 Если бы частица покоилась, то ее положение и импульс были бы определенными. Поскольку это не так, n должно иметь целочисленное значение. Дело не в том, что главное квантовое число может быть измерено только целыми числами, а в том, что гребень одной волны будет накладываться на впадину другой, и волна гаснет.
Если бы частица покоилась, то ее положение и импульс были бы определенными. Поскольку это не так, n должно иметь целочисленное значение. Дело не в том, что главное квантовое число может быть измерено только целыми числами, а в том, что гребень одной волны будет накладываться на впадину другой, и волна гаснет. - Чанг, Рэймонд. Физическая химия для биологических наук. 2005, Университетские научные книги. стр. 427-428.
- Гиллеспи, Рональд. Демистификация вводной химии. Форум: вклад Целевой группы по общей химии. 1996: 73; 617-622.
- Петруччи, Ральф. Общая химия: принципы и современные приложения, десятое издание.
- Предположим, что все, что вы знаете об определенном электроне, это то, что его главное квантовое число равно 3. Каковы возможные значения остальных четырех квантовых чисел?
- Возможно ли иметь электрон с такими квантовыми числами: \(n=2\), \(l=1\), \(m_l=3\), \(m_s=1/2\)? Почему или почему нет?
- Возможно ли иметь два электрона с одинаковыми \(n\), \(l\) и \(m_l\)?
- Сколько подоболочек находится на главном квантовом уровне \(n=3\)?
- Какой тип орбитали обозначается квантовыми числами \(n=4\), \(l=3\) и \(m_l=0\)?
- Когда \(n=3\), \(l=0\), \(m_l = 0\) и \(m_s=+1/2 \text{ или } -1/2\)
- \(l=1\), \(m_l = -1, 0 или +1\) и \(m_s=+1/2 \text{ или } -1/2\)
- \(l=2\), \(m_l = -2, -1, 0, 1, \text{ или }+2\) и \(m_s=+1/2 \text{ или } -1/ 2\)
- Нет, это невозможно.
 \(m_l=3\) не находится в диапазоне от \(-l\) до \(+l\). Значение должно быть равно -1, 0 или +1.
\(m_l=3\) не находится в диапазоне от \(-l\) до \(+l\). Значение должно быть равно -1, 0 или +1. - Да, возможно иметь два электрона с одинаковыми \(n\), \(l\) и \(m_l\). Спин одного электрона должен быть +1/2, а спин другого электрона должен быть -1/2.
- На главном квантовом уровне \(n=3\) есть три подоболочки.
- Поскольку \(l=3\) относится к подоболочке f, тип представленной орбитали — 4f (комбинация главного квантового числа n и имени подоболочки).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.

- Теги
- квантовые числа
- Три квантовых числа ( n , l и m ), которые описывают орбитальные целые числа: 0, 1, 2, 3 и так далее.
- Главное квантовое число ( n ) не может быть равно нулю. Допустимые значения n следовательно, это 1, 2, 3, 4 и так далее.
- Угловое квантовое число ( l ) может быть любым целым числом от 0 до n — 1. Если n = 3, например, l может быть 0, 1 или 2.
- Магнитное квантовое число ( m ) может быть любым целым числом от — до и + л . Если л = 2, м может быть либо -2, -1, 0, +1 или +2.
- Один электрон добавляется к каждой из вырожденных орбиталей в подоболочке перед двумя электроны присоединяются к любой орбитали в подоболочке.
- Электроны добавляются к подоболочке с тем же значением квантового числа спина до тех пор, пока каждая орбиталь в подоболочке имеет по крайней мере один электрон.
- Коэффициенты и пропорции
- Алгебраический Выражения
- Экспоненты
- Логарифмы
- Глоссарий и ссылки
В общей сложности четыре квантовых числа используются для полного описания движения и траекторий каждого электрона внутри атома.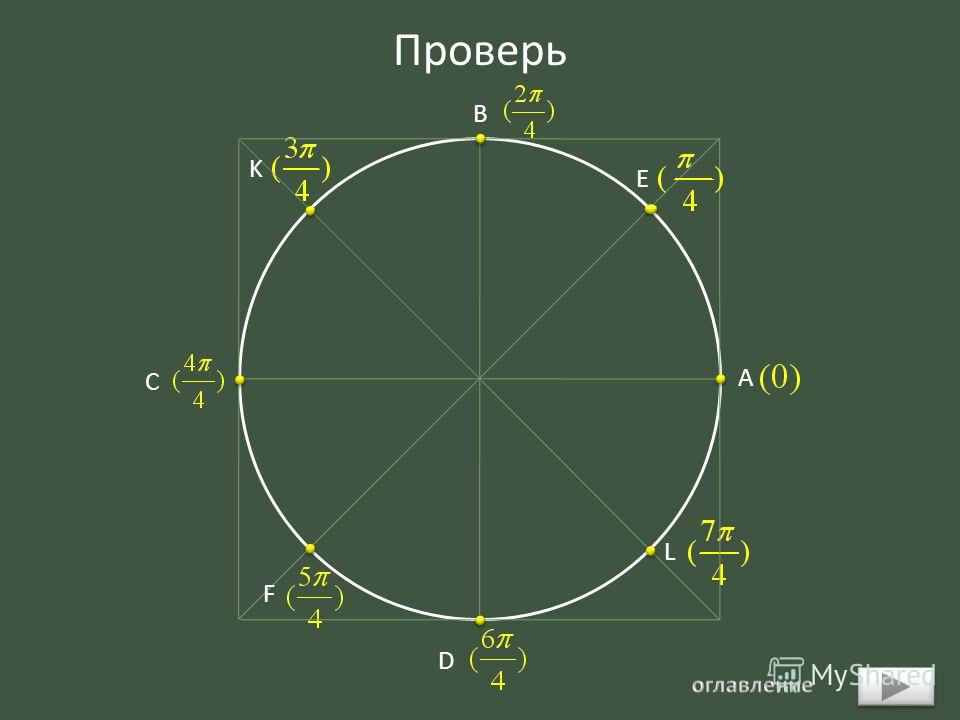 Комбинация всех квантовых чисел всех электронов в атоме описывается волновой функцией, удовлетворяющей уравнению Шредингера. Каждый электрон в атоме имеет уникальный набор квантовых чисел; Согласно принципу запрета Паули никакие два электрона не могут иметь одну и ту же комбинацию четырех квантовых чисел. Квантовые числа важны, потому что их можно использовать для определения электронной конфигурации атома и вероятного местоположения электронов атома. Квантовые числа также используются для понимания других характеристик атомов, таких как энергия ионизации и атомный радиус.
Комбинация всех квантовых чисел всех электронов в атоме описывается волновой функцией, удовлетворяющей уравнению Шредингера. Каждый электрон в атоме имеет уникальный набор квантовых чисел; Согласно принципу запрета Паули никакие два электрона не могут иметь одну и ту же комбинацию четырех квантовых чисел. Квантовые числа важны, потому что их можно использовать для определения электронной конфигурации атома и вероятного местоположения электронов атома. Квантовые числа также используются для понимания других характеристик атомов, таких как энергия ионизации и атомный радиус.
В атомах существует четыре квантовых числа: главное квантовое число ( n ), квантовое число орбитального углового момента ( l ), магнитное квантовое число ( m l ) и квантовое число спина электрона ( м с ). Главное квантовое число \(n\) описывает энергию электрона и наиболее вероятное расстояние электрона от ядра. Другими словами, это относится к размеру орбитали и энергетическому уровню, на котором находится электрон. Количество подоболочек, или \(l\), описывает форму орбитали. Его также можно использовать для определения количества угловых узлов. Магнитное квантовое число, m l описывает энергетические уровни в подоболочке, а m s относится к спину электрона, который может быть направлен вверх или вниз.
Количество подоболочек, или \(l\), описывает форму орбитали. Его также можно использовать для определения количества угловых узлов. Магнитное квантовое число, m l описывает энергетические уровни в подоболочке, а m s относится к спину электрона, который может быть направлен вверх или вниз.
Главное квантовое число (\(n\))
Главное квантовое число, \(n\), обозначает основную электронную оболочку. Поскольку n описывает наиболее вероятное расстояние электронов от ядра, чем больше число n , тем дальше от ядра находится электрон, тем больше размер орбитали и тем больше размер атома. n может быть любым положительным целым числом, начиная с 1, так как \(n=1\) обозначает первую основную оболочку (самую внутреннюю оболочку). Первая основная оболочка также называется основным состоянием или состоянием с наименьшей энергией. Это объясняет, почему \(n\) не может быть 0 или любым отрицательным целым числом, потому что не существует атомов с нулевым или отрицательным количеством энергетических уровней/основных оболочек. Когда электрон находится в возбужденном состоянии или получает энергию, он может перейти на вторую основную оболочку, где \(n=2\). Это называется поглощением, потому что электрон «поглощает» фотоны или энергию. Известная как эмиссия, электроны также могут «излучать» энергию, когда они прыгают на более низкие основные оболочки, где n уменьшается на целые числа. С увеличением энергии электрона увеличивается и главное квантовое число, например, 9.0026 n = 3 указывает на третью основную оболочку, n = 4 указывает на четвертую основную оболочку и так далее.
Когда электрон находится в возбужденном состоянии или получает энергию, он может перейти на вторую основную оболочку, где \(n=2\). Это называется поглощением, потому что электрон «поглощает» фотоны или энергию. Известная как эмиссия, электроны также могут «излучать» энергию, когда они прыгают на более низкие основные оболочки, где n уменьшается на целые числа. С увеличением энергии электрона увеличивается и главное квантовое число, например, 9.0026 n = 3 указывает на третью основную оболочку, n = 4 указывает на четвертую основную оболочку и так далее.
\[n=1,2,3,4…\]
Пример \(\PageIndex{1}\)
Если n = 7, то какова главная электронная оболочка?
Пример \(\PageIndex{2}\)
Если электрон перепрыгнул с уровня энергии n = 5 на уровень энергии n = 3, произошло ли поглощение или испускание фотона?
Квантовое число орбитального углового момента (\(l\))
Квантовое число орбитального углового момента \(l\) определяет форму орбитали и, следовательно, угловое распределение. Количество угловых узлов равно значению квантового числа углового момента \(l\). (Для получения дополнительной информации об угловых узлах см. Электронные орбитали.) Каждое значение \(l\) указывает на конкретную подоболочку s, p, d, f (каждая уникальна по форме). Значение \(l\) зависит от главное квантовое число \(n\). В отличие от \(n\), значение \(l\) может быть равно нулю. Это также может быть положительное целое число, но оно не может быть больше, чем на единицу меньше главного квантового числа (\(n-1\)):
\[l=0, 1, 2, 3, 4…, (n-1)\]
Пример \(\PageIndex{3}\)
Если \(n = 7\), какие возможные значения \(l\)?
Пример \(\PageIndex{4}\)
Если \(l = 4\), сколько угловых узлов имеет атом?
Магнитное квантовое число (\(m_l\))
Магнитное квантовое число \(m_l\) определяет количество орбиталей и их ориентацию внутри подоболочки. Следовательно, его значение зависит от квантового числа орбитального углового момента \(l\). При заданном \(l\) \(m_l\) представляет собой интервал от \(–l\) до \(+l\), поэтому он может быть нулем, отрицательным целым числом или положительным целым числом.
\[m_l= -l, (-l +1),(-l +2),…, -2, -1, 0, 1, 2, … (l – 1), (l – 2), +l\]
Пример \(\PageIndex{5}\)
Пример: Если \(n=3\) и \(l=2\), то каковы возможные значения \(m_l\) ?
Квантовое число спина электрона (\(m_s\))
В отличие от \(n\), \(l\) и \(m_l\), квантовое число спина электрона \(m_s\) не зависит от другое квантовое число. Он обозначает направление вращения электрона и может иметь спин +1/2, представленный ↑, или -1/2, представленный ↓. Это означает, что когда \(m_s\) положителен, электрон имеет восходящий спин, который можно назвать «спин вверх». Когда он отрицательный, электрон имеет нисходящий спин, поэтому он «спин нисходящий». Значение квантового числа спина электрона состоит в том, что оно определяет способность атома генерировать магнитное поле или нет. (Электронный спин.)
\[m_s= \pm \dfrac{1}{2}\]
Пример \(\PageIndex{5}\)
Перечислите возможные комбинации всех четырех квантовых чисел, когда \(n=2\), \(l=1\) и \(m_l=0\).
Пример \(\PageIndex{6}\)
Может ли электрон с \(m_s=1/2\) иметь направленный вниз спин?
Пристальный взгляд на оболочки, подоболочки и орбитали
Основные оболочки
Значение главного квантового числа n — это уровень главной электронной оболочки (главный уровень). Все орбитали с одинаковым значением n находятся на одном главном уровне. Например, все орбитали на втором главном уровне имеют главное квантовое число n=2. Чем выше значение n, тем больше количество основных электронных оболочек. Это приводит к большему расстоянию между самым дальним электроном и ядром. В результате увеличивается размер атома и его атомный радиус.
Поскольку радиус атома увеличивается, электроны удаляются от ядра. Таким образом, атому легче вытолкнуть электрон, потому что ядро не оказывает на него такого сильного притяжения, и энергия ионизации уменьшается.
Пример \(\PageIndex{7}\)
Какая орбиталь имеет более высокую энергию ионизации: \(n=3\) или \(n=2\)?
Подоболочки
Количество значений орбитального углового числа l также можно использовать для определения количества подоболочек в главной электронной оболочке:
После рассмотрения приведенных выше примеров мы видим, что значение n равно количеству подоболочек в основной электронной оболочке:
Чтобы определить тип возможных подоболочек n, этим подоболочкам были присвоены буквенные имена. Значение l определяет имя подоболочки:
Значение l определяет имя подоболочки:
| Название подоболочки | Значение \(л\) |
|---|---|
| подоболочка | 0 |
| р подоболочка | 1 |
| d подоболочка | 2 |
| f подоболочка | 3 |
Следовательно:
Мы можем обозначить главное квантовое число n и определенную подоболочку, комбинируя значение n и имя подоболочки (которое можно найти с помощью l). Например, 3p относится к третьему главному квантовому числу (n=3) и подоболочке p (l=1).
Например, 3p относится к третьему главному квантовому числу (n=3) и подоболочке p (l=1).
Пример \(\PageIndex{8}\)
Как называется орбиталь с квантовыми числами n=4 и l=1?
Пример \(\PageIndex{9}\)
Как называются орбитали с квантовым числом n=3?
Орбитали
Количество орбиталей в подоболочке эквивалентно количеству значений, которые принимает магнитное квантовое число ml. Полезным уравнением для определения количества орбиталей в подоболочке является 2l +1. Это уравнение даст вам не значение ml, а число возможных значений, которые может принимать ml на конкретной орбитали. Например, если l=1 и ml может принимать значения -1, 0 или +1, значение 2l+1 будет равно трем и будет три различных орбитали. Названия орбиталей названы в честь подоболочек, в которых они находятся:
Например, если l=1 и ml может принимать значения -1, 0 или +1, значение 2l+1 будет равно трем и будет три различных орбитали. Названия орбиталей названы в честь подоболочек, в которых они находятся:
| s-орбитали | р-орбитали | d-орбитали | f орбитали | |
|---|---|---|---|---|
| л | 0 | 1 | 2 | 3 |
| м л | 0 | -1, 0, +1 | -2, -1, 0, +1, +2 | -3, -2, -1, 0, +1, +2, +3 |
| Количество орбиталей в указанной подоболочке | 1 | 3 | 5 | 7 |
На рисунке ниже мы видим примеры двух орбиталей: p-орбиталь (синяя) и s-орбиталь (красная). Красная s-орбиталь — это 1s-орбиталь. Чтобы изобразить 2s-орбиталь, представьте слой, похожий на поперечное сечение челюсти, вокруг круга. Слои изображают угловые узлы атомов. Чтобы изобразить 3s-орбиталь, представьте еще один слой вокруг круга и так далее и тому подобное. Орбиталь p похожа на форму гантели, ее ориентация внутри подоболочки зависит от m л . Форма и ориентация орбитали зависят от l и m l .
Красная s-орбиталь — это 1s-орбиталь. Чтобы изобразить 2s-орбиталь, представьте слой, похожий на поперечное сечение челюсти, вокруг круга. Слои изображают угловые узлы атомов. Чтобы изобразить 3s-орбиталь, представьте еще один слой вокруг круга и так далее и тому подобное. Орбиталь p похожа на форму гантели, ее ориентация внутри подоболочки зависит от m л . Форма и ориентация орбитали зависят от l и m l .
Чтобы визуализировать и систематизировать первые три квантовых числа, мы можем думать о них как о составных частях дома. На следующем изображении крыша представляет главное квантовое число n, каждый уровень представляет подоболочку l, а каждая комната представляет различные орбитали ml в каждой подоболочке. Орбиталь s, поскольку значение ml может быть только 0, может существовать только в одной плоскости. Однако p-орбиталь имеет три возможных значения ml и, следовательно, три возможные ориентации орбиталей, показанные Px, Py и Pz. Паттерн продолжается: орбиталь d содержит 5 возможных орбитальных ориентаций, а f имеет 7:9. 0024
0024
Еще одним полезным наглядным пособием для рассмотрения возможных орбиталей и подоболочек с набором квантовых чисел будет диаграмма электронной орбиты. (Дополнительные диаграммы электронных орбит см. в разделе « Конфигурации электронов» .) Характеристики каждого квантового числа изображены в разных областях этой диаграммы.
Ограничения
Ссылки
Проблемы
Решения
Авторы и авторство
Quantum Numbers for Atoms распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.
Квантовые числа и конфигурации электронов
Квантовые числа и конфигурации электроновКвантовые числа и электрон Конфигурации
| Квантовые числа | Правила, управляющие квантовыми числами | Оболочки и подоболочки орбиталей | Возможные комбинации квантовых чисел | Таблица: Сводка допустимых комбинаций Quantum Номера |
| Относительные энергии атомных орбиталей | электронных конфигураций, принцип Ауфбау, Вырожденные орбитали и правило Хунда 90 243 Таблица | : Электронные конфигурации элементов | Исключения для предсказанных электронных конфигураций | Электронные конфигурации и периодическая таблица |
Квантовые числа
Модель Бора была одномерной моделью, которая использовала одно квантовое число для описания
распределение электронов в атоме. Единственная информация, которая была важна, это размер .
орбиты, которая описывалась квантовым числом n . модель Шредингера
позволил электрону занять трехмерное пространство. Поэтому потребовалось три
координаты, или три квантовых чисел , чтобы описать орбитали, на которых электроны
можно найти.
Единственная информация, которая была важна, это размер .
орбиты, которая описывалась квантовым числом n . модель Шредингера
позволил электрону занять трехмерное пространство. Поэтому потребовалось три
координаты, или три квантовых чисел , чтобы описать орбитали, на которых электроны
можно найти.
Три координаты, полученные из волновых уравнений Шредингера, являются главной ( n ), угловое ( l ) и магнитное ( m ) квантовые числа. Эти квантовые числа описывают размер, форму и ориентацию в пространстве орбиталей атома.
Главное квантовое число ( n ) описывает размер орбитали.
орбитали, для которых n = 2 больше, чем те, для которых n = 1, например.
Поскольку они имеют противоположные электрические заряды, электроны притягиваются к ядру
атом. Следовательно, энергия должна быть поглощена, чтобы возбудить электрон с орбитали, на которой
электрон приближается к ядру ( n = 1) на орбиталь, на которой он дальше
от ядра ( n = 2). Таким образом, главное квантовое число косвенно
описывает энергию орбитали.
Таким образом, главное квантовое число косвенно
описывает энергию орбитали.
Угловое квантовое число ( l ) описывает форму орбитали. Орбитали имеют форму, которую лучше всего описать как сферическую ( l = 0), полярную ( l = 1), или клеверный лист ( l = 2). Они могут даже принимать более сложные формы в качестве значения углового квантового числа становится больше.
Существует только один способ ориентации сферы ( l = 0) в пространстве.
Орбитали, имеющие полярные ( l = 1) или формы клеверного листа ( l = 2), однако, могут
указывают в разные стороны. Поэтому нам нужно третье квантовое число, известное как магнитное число .
квантовое число ( m ), чтобы описать ориентацию в пространстве конкретного
орбитальный. (Оно называется магнитным квантовым числом , потому что влияние различных
Ориентация орбиталей впервые наблюдалась в присутствии магнитного поля. )
)
Правила, регулирующие разрешенные комбинации Квантовые числа
| Практическая задача 7: Опишите разрешенные комбинации n , l и m квантовых чисел, когда n = 3, Нажмите здесь, чтобы проверьте свой ответ на практическое задание 7 |
Оболочки и подоболочки орбиталей
Орбитали с одинаковым значением главного квантового числа образуют оболочка . Орбитали внутри оболочки делятся на подоболочек , которые имеют одинаковое значение
угловое квантовое число. Химики описывают оболочку и подоболочку, в которой орбиталь
принадлежит двухсимвольному коду, такому как 2 p или 4 f . Первый персонаж
указывает на оболочку ( n = 2 или n = 4). Второй символ определяет
подоболочка. По соглашению следующие строчные буквы используются для обозначения различных
подоболочки.
Орбитали внутри оболочки делятся на подоболочек , которые имеют одинаковое значение
угловое квантовое число. Химики описывают оболочку и подоболочку, в которой орбиталь
принадлежит двухсимвольному коду, такому как 2 p или 4 f . Первый персонаж
указывает на оболочку ( n = 2 или n = 4). Второй символ определяет
подоболочка. По соглашению следующие строчные буквы используются для обозначения различных
подоболочки.
| с : | л = 0 | |
| р : | л = 1 | |
| д : | л = 2 | |
| ф : | л = 3 |
Хотя в первых четырех буквах нет шаблона ( s , p , d , f ),
буквы идут от этой точки в алфавитном порядке ( g , h и т. д.). Немного
допустимых комбинаций квантовых чисел n и l показаны на
рисунок ниже.
д.). Немного
допустимых комбинаций квантовых чисел n и l показаны на
рисунок ниже.
Третье правило, ограничивающее допустимые комбинации n , л и м квантовые числа имеют важное следствие. Это заставляет количество подоболочек в оболочке быть равным главному квантовому числу оболочки. Корпус n =3, для Например, содержит три подоболочки: орбитали 3 s , 3 p и 3 d .
Возможные комбинации квантовых чисел
Есть только одна орбиталь в n = 1 оболочка, потому что есть только один вход которым шар можно ориентировать в пространстве. Единственная допустимая комбинация квантовых чисел для которого n = 1 имеет место следующее.
| нет | л | м | ||||
| 1 | 0 | 0 | 1с |
В оболочке n = 2 четыре орбитали.
| нет | л | м | ||||
| 2 | 0 | 0 | 2 с |
| 2 | 1 | -1 | ||||
| 2 | 1 | 0 | 2 шт. | |||
| 2 | 1 | 1 |
В подоболочке 2 s имеется только одна орбиталь. Но есть три орбитали в
подоболочку 2 p , потому что есть три направления, в которых орбиталь p может
точка. Одна из этих орбиталей ориентирована по оси X , другая — по оси Y . оси, а третья по оси Z системы координат, как показано на рисунке
ниже. Поэтому эти орбитали известны как 2 р х , 2 р у ,
и 2 p z орбиталей.
оси, а третья по оси Z системы координат, как показано на рисунке
ниже. Поэтому эти орбитали известны как 2 р х , 2 р у ,
и 2 p z орбиталей.
В оболочке n = 3 девять орбиталей.
| нет | л | м | ||||
| 3 | 0 | 0 | 3 с | |||
| 3 | 1 | -1 | ||||
| 3 | 1 | 0 | 3 р | |||
| 3 | 1 | 1 | ||||
| 3 | 2 | -2 | ||||
| 3 | 2 | -1 | 3 д | |||
| 3 | 2 | 0 | ||||
| 3 | 2 | 1 | ||||
| 3 | 2 | 2 |
Имеется одна орбиталь в подоболочке 3 s и три орбитали в 3 p подоболочка. Однако оболочка n = 3 включает также 3 d орбиталей.
Однако оболочка n = 3 включает также 3 d орбиталей.
Пять различных ориентаций орбиталей в подоболочке 3 d показаны на рисунок ниже. Одна из этих орбиталей лежит в плоскости XY XYZ . систему координат и называется 3 d xy орбитальная. 3 д хз и 3 d yz орбитали имеют одинаковую форму, но лежат между осями система координат в плоскостях XZ и YZ . Четвертая орбиталь в этом подоболочка лежит вдоль осей X и Y и называется орбитальный. Большая часть пространства, занимаемого пятой орбиталью, лежит вдоль Z ось и эта орбиталь называется орбиталью 3 d z 2 .
Число орбиталей в оболочке равно квадрату главного квантового числа: 1 2 = 1, 2 2 = 4, 3 2 = 9. В подоболочке s имеется одна орбиталь ( l = 0), три орбитали в подоболочке p ( l = 1) и пять орбиталей в подоболочке d подоболочка ( л = 2). Таким образом, количество орбиталей в подоболочке равно 2( l ) +
1.
Таким образом, количество орбиталей в подоболочке равно 2( l ) +
1.
Прежде чем мы сможем использовать эти орбитали, нам нужно знать количество электронов, которые могут занимают орбиталь и как их можно отличить друг от друга. Экспериментальный данные свидетельствуют о том, что орбиталь может содержать не более двух электронов.
Чтобы различить два электрона на орбитали, нам нужен четвертый квант количество. Это называется спиновое квантовое число ( с ), потому что электроны ведут себя как если бы они вращались либо по часовой стрелке, либо против часовой стрелки. Один из электронам на орбитали произвольно присваивается s квантовое число +1/2, другому присваивается s квантовое число -1/2. Таким образом, требуется три квантовых числа чтобы определить орбиталь, но четыре квантовых числа, чтобы идентифицировать один из электронов, который может занимают орбиталь.
Допустимые комбинации n , l и m квантовых чисел для
первые четыре оболочки приведены в таблице ниже. На каждую из этих орбиталей приходится две
допустимые значения квантового числа спина, с .
На каждую из этих орбиталей приходится две
допустимые значения квантового числа спина, с .
| Апплет, показывающий атомные и молекулярные орбитали из |
Сводка допустимых комбинаций Quantum Числа
| нет | л | м | Обозначение подоболочки | Количество орбиталей в подоболочке | Количество электронов, необходимое для заполнения подоболочки | Общее количество электронов в подоболочке | |||||
| 1 | 0 | 0 | 1с | 1 | 2 | 2 | |||||
| 2 | 0 | 0 | 2 с | 1 | 2 | ||||||
| 2 | 1 | 1,0,-1 | 2 шт. | 3 | 6 | 8 | |||||
| 3 | 0 | 907:10 | 0 | 3 с | 1 | 2 | |||||
| 3 | 1 | 1,0,-1 | 3 шт. | 3 | 6 | ||||||
| 3 | 2 | 2,1,0,-1,-2 | 3д | 5 | 10 | 18 | |||||
| 4 | 0 | 0 | 4с | 1 | 2 | ||||||
| 4 | 1 | 1,0,-1 | 4 шт. | 3 | 6 | ||||||
| 4 | 2 | 2,1,0,-1,-2 | 4д | 5 | 10 | ||||||
| 4 | 3 | 3,2,1,0,-1,-2,-3 | 4ф | 7 | 14 | 32 | |||||
Относительные энергии атомных орбиталей
Из-за силы притяжения между объектами противоположного заряда, наиболее
важным фактором, влияющим на энергию орбитали, является ее размер и, следовательно, значение
главного квантового числа, н . Для атома, содержащего только один электрон,
нет разницы между энергиями различных подоболочек внутри оболочки.
Например, орбитали 3 s , 3 p и 3 d имеют одинаковую энергию в
атом водорода. Модель Бора, определяющая энергии орбит с точки зрения ничего.
больше, чем расстояние между электроном и ядром, поэтому работает для этого
атом.
Для атома, содержащего только один электрон,
нет разницы между энергиями различных подоболочек внутри оболочки.
Например, орбитали 3 s , 3 p и 3 d имеют одинаковую энергию в
атом водорода. Модель Бора, определяющая энергии орбит с точки зрения ничего.
больше, чем расстояние между электроном и ядром, поэтому работает для этого
атом.
Однако атом водорода необычен. Как только атом содержит более одного электрон, разные подоболочки уже не имеют одинаковую энергию. Внутри данной оболочки s орбиталей всегда имеют наименьшую энергию. Энергия подоболочек постепенно становится тем больше, чем больше значение углового квантового числа.
Относительные энергии: с < p < d < f
В результате два фактора контролируют энергию орбитали в большинстве случаев. атомов: размер орбитали и ее форма, как показано на рисунке ниже.
атомов: размер орбитали и ее форма, как показано на рисунке ниже.
Можно сконструировать очень простое устройство для оценки относительного энергии атомных орбиталей. Допустимые комбинации квантов n и l числа организованы в таблицу, как показано на рисунке ниже, и стрелки нарисованы на 45 углы в градусах, направленные в левый нижний угол таблицы.
Затем считывается порядок возрастания энергии орбиталей, следуя этим стрелки, начиная с верхней части первой строки и затем переходя ко второй, третьей, четвертая строка и так далее. Эта диаграмма предсказывает следующий порядок увеличения энергии для атомных орбиталей.
1 с < 2 с < 2 с < 3 с < 3 с <4 с < 3 d <4 p < 5 с < 4 d < 5 p < 6 с < 4 f < 5 d < 6 p < 7 с < 5 f < 6 д < 7 р < 8 с . ..
..
| Щелкните здесь для дополнительной практики Проблемы |
Электронные конфигурации, принцип Ауфбау, Вырожденные орбитали и правило Хунда
Электронная конфигурация атома описывает орбитали, занятые электроны на атоме. В основе этого предсказания лежит правило, известное как ауфбау принцип , который предполагает, что электроны добавляются к атому по одному, начиная с наименьшей энергетической орбиталью, пока все электроны не будут помещены в соответствующую орбиту.
Атом водорода ( Z = 1) имеет только один электрон, который переходит в самую низкую энергию орбитальная, орбитальная 1 с . На это указывает надстрочный индекс «1». после символа орбитали.
Ч ( Z = 1): 1 с 1
Следующий элемент имеет два электрона, и второй электрон заполняет орбиталь 1 s потому что есть только два возможных значения для спинового квантового числа, используемого для различения
между электронами на орбитали.
He ( Z = 2): 1 с 2
Третий электрон переходит на следующую орбиталь на энергетической диаграмме 2 с орбитальный.
Li ( Z = 3): 1 с 2 2 с 1
Четвертый электрон заполняет эту орбиталь.
Be ( Z = 4): 1 с 2 2 с 2
После заполнения орбиталей 1 s и 2 s следующая самая низкая энергия орбитали — это три орбитали 2 p . Таким образом, пятый электрон переходит в один из эти орбитали.
B ( Z = 5): 1 с 2 2 с 2 2 р 1
Когда приходит время добавить шестой электрон, электронная конфигурация становится очевидной.
C ( Z = 6): 1 с 2 2 с 2 2 р 2
Однако в подоболочке 2 p есть три орбитали. Второй электрон
на ту же орбиталь, что и первая, или на одну из других орбиталей в
эта подоболочка?
Второй электрон
на ту же орбиталь, что и первая, или на одну из других орбиталей в
эта подоболочка?
Чтобы ответить на этот вопрос, нам нужно понять концепцию вырожденных орбиталей . По определение, орбитали вырождены , когда они имеют одинаковую энергию. Энергия орбиталь зависит как от ее размера, так и от ее формы, потому что электрон тратит больше своего время дальше от ядра атома по мере того, как орбиталь становится больше или форма становится более сложным. Однако в изолированном атоме энергия орбитали не зависит от направления, в котором он указывает в пространстве. орбитали, отличающиеся только своей ориентация в пространстве, например, 2 p x , 2 p y и 2 p z орбитали, следовательно, вырождены.
Электроны заполняют вырожденные орбитали в соответствии с правилами, впервые сформулированными Фридрихом Хундом. Хунда
правила можно резюмировать следующим образом.
Когда приходит время поместить два электрона в подоболочку 2 p , мы помещаем один электрон на каждую из двух этих орбиталей. (выбор между 2 р х , 2 p y и 2 p z орбиталей является чисто произвольным.)
C ( Z = 6): 1 с 2 2 с 2 2 р x 1 2 р у 1
Тот факт, что оба электрона в подоболочке 2 p имеют одинаковый спин Квантовое число можно показать, представив электрон, для которого с = +1/2 с
стрелка вверх и электрон, для которого с = -1/2 со стрелкой
вниз.
Таким образом, электроны на 2 p орбиталях углерода можно представить в виде следует.
Когда мы получим N ( Z = 7), мы должны поместить по одному электрону в каждую из трех вырожденных 2 p орбиталей.
| Н ( З = 7): | 1 с 2 2 с 2 2 р 3 |
Поскольку каждая орбиталь в этой подоболочке теперь содержит один электрон, следующий электрон добавленные к подоболочке, должны иметь противоположное спиновое квантовое число, тем самым заполняя одно из 2 p орбиталей.
| О ( Z = 8): | 1 с 2 2 с 2 2 р 4 |
Девятый электрон заполняет вторую орбиталь в этой подоболочке.
| Ж ( З = 9): | 1 с 2 2 с 2 2 р 5 |
Десятый электрон завершает подоболочку 2 p .
| Ne ( Z = 10): | 1 с 2 2 с 2 2 р 6 |
Есть что-то необычайно стабильное в атомах, таких как He и Ne, у которых есть электроны.
конфигурации с заполненными оболочками орбиталей. Поэтому по соглашению мы пишем
сокращенные электронные конфигурации с точки зрения числа электронов за
предыдущий элемент с электронной конфигурацией заполненной оболочки. Электронные конфигурации
следующие два элемента в периодической таблице, например, могут быть записаны следующим образом.
Электронные конфигурации
следующие два элемента в периодической таблице, например, могут быть записаны следующим образом.
Na ( Z = 11): [Ne] 3 с 1
Mg ( Z = 12): [Ne] 3 с 2
| Практическая задача 8: Предсказать электрон конфигурация для нейтрального атома олова (Sn, Z = 50). Нажмите здесь, чтобы проверьте свой ответ на практическое задание 8 |
Процесс Ауфбау можно использовать для предсказания электронной конфигурации элемента.
Фактическая конфигурация, используемая элементом, должна быть определена экспериментально.
экспериментально определенные электронные конфигурации для элементов в первых четырех строках
Периодической таблицы приведены в таблице в следующем разделе.
| Учебная деятельность |
| Щелкните здесь для дополнительной практики Проблемы |
Электронные конфигурации элементов
(элементы 1, 2, 3 и 4 ряда)
| Атомный номер | Символ | Электронная конфигурация | ||
| 1 | Х | 1 с 1 | ||
| 2 | Он | 1 с 2 = [Не] | ||
| 3 | Ли | [Не] 2 с 1 | ||
| 4 | Быть | [Не] 2 с 2 | ||
| 5 | Б | [Не] 2 с 2 2 р 1 | ||
| 6 | С | [He] 2 с 2 2 р 2 | ||
| 7 | Н | [He] 2 с 2 2 р 3 | ||
| 8 | О | 907:10[He] 2 с 2 2 р 4 | ||
| 9 | Ф | [He] 2 с 2 2 р 5 | ||
| 10 | Не | [He] 2 с 2 2 p 6 = [Ne] | ||
| 11 | На | [Не] 3 с 1 | ||
| 12 | мг | [Не] 3 с 2 | ||
| 13 | Ал | [Ne] 3 с 2 3 р 1 | ||
| 14 | Си | [Ne] 3 с 2 3 р 2 | ||
| 15 | Р | [Ne] 3 с 2 3 р 3 | ||
| 16 | С | [Ne] 3 с 2 3 р 4 | ||
| 17 | Кл | [Ne] 3 с 2 3 р 5 | ||
| 18 | Ар | [Ne] 3 s 2 3 p 6 = [Ar] | ||
| 19 | К | 907:10[Ar] 4 с 1 | ||
| 20 | Са | [Ar] 4 с 2 | ||
| 21 | Sc | [Ar] 4 с 2 3 d 1 | ||
| 22 | Ти | 907:10[Ar] 4 с 2 3 d 2 | ||
| 23 | В | [Ar] 4 с 2 3 d 3 | ||
| 24 | Кр | [Ar] 4 с 1 3 d 5 | ||
| 25 | Мн | [Ar] 4 с 2 3 d 5 | ||
| 26 | Фе | [Ar] 4 с 2 3 d 6 | ||
| 27 | Сотрудничество | [Ar] 4 с 2 3 д 7 | ||
| 28 | Ni | [Ar] 4 с 2 3 d 8 | ||
| 29 | Медь | [Ar] 4 с 1 3 d 10 | ||
| 30 | Цинк | 907:10[Ar] 4 с 2 3 d 10 | ||
| 31 | Га | [Ar] 4 s 2 3 d 10 4 p 1 | ||
| 32 | Гэ | [Ar] 4 с 2 3 д 10 4 р 2 | ||
| 33 | Как | [Ar] 4 s 2 3 d 10 4 p 3 | ||
| 34 | Se | [Ar] 4 s 2 3 d 10 4 p 4 | ||
| 35 | Бр | [Ar] 4 s 2 3 d 10 4 p 5 | ||
| 36 | Кр | [Ar] 4 s 2 3 d 10 4 p 6 = [Kr] | ||
Исключения из предсказанных электронных конфигураций
Существует несколько моделей электронных конфигураций, перечисленных в таблице в
предыдущий раздел. Одним из наиболее поразительных является замечательный уровень согласия между
эти конфигурации и конфигурации, которые мы могли бы предсказать. Есть только два
исключения среди первых 40 элементов: хром и медь.
Одним из наиболее поразительных является замечательный уровень согласия между
эти конфигурации и конфигурации, которые мы могли бы предсказать. Есть только два
исключения среди первых 40 элементов: хром и медь.
Строгое соблюдение правил процесса ауфбау может привести к следующему: электронные конфигурации хрома и меди.
| предсказанных электронных конфигураций: | Cr ( Z = 24): [Ar] 4 s 2 3 d 4 | |
| Cu ( Z = 29): [Ar] 4 s 2 3 d 9 |
Экспериментально определенные электронные конфигурации для этих элементов слегка другой.
| фактические электронные конфигурации: | Cr ( Z = 24): [Ar] 4 s 1 3 d 5 | |
| Cu ( Z = 29): [Ar] 4 s 1 3 d 10 |
В каждом случае один электрон был перенесен с 4 s орбитальная к 3 d орбитали, хотя предполагается, что орбитали 3 d находятся на более высоком уровне, чем
4 с орбитальная.
Как только мы преодолеем атомный номер 40, разница между энергиями соседних орбиталей настолько мала, что становится намного легче перенести электрон с одной орбитальный к другому. Большинство исключений из электронной конфигурации, предсказанных из поэтому показанная ранее диаграмма ауфбау встречается среди элементов с атомными номерами больше 40. Хотя заманчиво сосредоточить внимание на горстка элементов, электронные конфигурации которых отличаются от предсказанных с диаграммой Ауфбау удивительно то, что эта простая диаграмма работает для столь многих элементы.
Электронные конфигурации и периодическая таблица
Когда данные электронной конфигурации расположены так, что мы можем сравнивать элементы в одном из
горизонтальные строки периодической таблицы, мы находим, что эти строки обычно соответствуют
заполнение оболочки орбиталей. Вторая строка, например, содержит элементы в
которой заполнены орбитали в оболочке n = 2.
| Ли ( Z = 3): | [Не] 2 с 1 | |
| Be ( Z = 4): | [Не] 2 с 2 | |
| Б ( З = 5): | [He] 2 с 2 2 р 1 | |
| С ( З = 6): | [He] 2 с 2 2 р 2 | |
| Н ( З = 7): | [He] 2 с 2 2 р 3 | |
| О ( Z = 8): | [He] 2 с 2 2 р 4 | |
| Ж ( З = 9): | [He] 2 с 2 2 р 5 | |
| Ne ( Z = 10): | [He] 2 с 2 2 р 6 |
В вертикальных столбцах или группах периодического
также стол. Элементы в группе имеют сходные конфигурации для своих внешних
электроны. Эту взаимосвязь можно увидеть, посмотрев на электронные конфигурации
элементы в столбцах по обе стороны периодической таблицы.
Элементы в группе имеют сходные конфигурации для своих внешних
электроны. Эту взаимосвязь можно увидеть, посмотрев на электронные конфигурации
элементы в столбцах по обе стороны периодической таблицы.
| Группа IA | Группа VIIA | |||||
| Н | 1 с 1 | |||||
| Ли | [Не] 2 с 1 | Ф | [He] 2 с 2 2 р 5 | |||
| Нет данных | [Не] 3 с 1 | Кл | [Ne] 3 с 2 3 р 5 | |||
| К | [Ар] 4 с 1 | Бр | [Ar] 4 s 2 3 d 10 4 p 5 | |||
| Руб | [Кр] 5 с 1 | я | [Kr] 5 с 2 4 d 10 5 р 5 | |||
| цезий | [Хе] 6 с 1 | В | [Xe] 6 s 2 4 f 14 5 d 10 6 p 6 3 5 3 |
На рисунке ниже показана взаимосвязь между таблицей Менделеева и орбиталями. заполняется в процессе ауфбау. Два столбца в левой части периодического
таблица соответствует заполнению 905:40 с орбитальная. Следующие 10 столбцов включают
элементы, в которых заполнены пять орбиталей подоболочки d . Шесть столбцов на
справа представлено заполнение трех орбиталей в подоболочке p . Наконец,
14 столбцов внизу таблицы соответствуют заполнению семи орбиталей в
подоболочка f .
заполняется в процессе ауфбау. Два столбца в левой части периодического
таблица соответствует заполнению 905:40 с орбитальная. Следующие 10 столбцов включают
элементы, в которых заполнены пять орбиталей подоболочки d . Шесть столбцов на
справа представлено заполнение трех орбиталей в подоболочке p . Наконец,
14 столбцов внизу таблицы соответствуют заполнению семи орбиталей в
подоболочка f .
| Практическая задача 9: Предсказать электрон конфигурации для кальция ( Z = 20) и цинка ( Z = 30) по их позициям в периодическая таблица. Нажмите здесь, чтобы проверьте свой ответ на практическое задание 9 |
Что такое показатель?
МАТЕМАТИКА ОБЗОР: ПОЛЕЗНАЯ МАТЕМАТИКА ДЛЯ КАЖДОГО СЕКЦИЯ
3. 2. Что такое ЭКСПОНЕНТ?
2. Что такое ЭКСПОНЕНТ?
вернуться к Экспоненты, стр. 1
Сначала давайте посмотрим, как работать с переменными в заданной степени, например, 3 .
Там пять правил работы с экспонентами:
1. a м * a n = a (m+n)
2. (а * б) н = а н * б н
3. (а м ) н = а (м * н)
4. а м / а н = а (м-н)
5.
(а/б) н = а н / б н
Давайте подробно рассмотрим каждый из них.
1. a m * a n = a (m+n) говорит, что когда вы берете число а, умноженное само на себя m раз и умноженное на одно и то же число a, умноженное само на себя n раз, это то же самое, что взять это число а и возведение его в степень, равную сумме m + n.
Вот пример, где
а = 3
м = 4
n = 5а м * a n = a (m+n)
3 4 * 3 5 = 3 (4+5) = 3 9 = 19 683
2. (а * б) н =
a n * b n говорит, что при умножении
два числа, а затем умножить это произведение само на себя n раз, это
то же самое, что умножить первое число само на себя n раз и умножить
что на второе число, умноженное само на себя n раз.
Давайте разработаем пример, где
а = 3
б = 6
н = 5(а * б) н = а н * б н
(3 * 6) 5 = 3 5 * 6 5
18 5 = 3 5 * 6 5 = 243 * 7 776 = 1 889 568
3. (а м ) н = a (m*n) говорит, что когда берешь число, a , и умножьте его само на себя m раз, затем умножьте это произведение само по себе n раз, это то же самое, что умножить число a сам по себе m * n раз.
Давайте разработаем пример где
а = 3
м = 4
n = 5( м ) н = (м * п)
(3 4 ) 5 = 3 (4 * 5) = 3 20 = 3 486 784 401
4. a m / a n = (м-н) говорит, что когда вы
возьми число а и умножь его само на себя m раз, затем раздели
это произведение на а, умноженное само на себя в n раз, это то же самое
как умноженное само на себя m-n раз.
a m / a n = (м-н) говорит, что когда вы
возьми число а и умножь его само на себя m раз, затем раздели
это произведение на а, умноженное само на себя в n раз, это то же самое
как умноженное само на себя m-n раз.
Вот пример, где
а = 3
м = 4
п = 5а м / а н = а (м-н)
3 4 / 3 5 = 3 (4-5) = 3 -1 (Запомните, как поднять число в отрицательную степень.)
3 4 / 3 5 = 1/3 1 = 1/3
5. (а/б) н = н / б н говорит
что при делении числа а на другое число b, а затем
умножь это частное
само по себе n раз, это то же самое, что умножить число само на себя
n раз, а затем разделив это произведение на число b, умноженное на
сам по себе n раз.

 46 ч. 1 п. 4, это когда к судебному приставу поступил исполнительный лист на взыскание денег, но, после проведения работы по установлению материального положения должника выясняется, что доходов, имущества и денег у него нет.
46 ч. 1 п. 4, это когда к судебному приставу поступил исполнительный лист на взыскание денег, но, после проведения работы по установлению материального положения должника выясняется, что доходов, имущества и денег у него нет.
 °-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
 °}}=\)
°}}=\)
 Значит, знак будет плюс;
Значит, знак будет плюс; Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\)
Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\) Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.
Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
\((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
 ..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
 Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
 104 Конституции РФ законопроекты вносятся в ГД субъектами права законодательной инициативы: Президентом РФ, СФ, сенаторами РФ, депутатами ГД, Правительством РФ, законодательными (представительными) органами государственной власти субъектов РФ. Право законодательной инициативы принадлежит также Конституционному Суду РФ, Верховному Суду РФ по вопросам их ведения. Законопроекты о введении или отмене налогов, освобождении от их уплаты, о выпуске государственных займов, об изменении финансовых обязательств государства, др. законопроекты, предусматривающие расходы, покрываемые за счет федерального бюджета, могут быть внесены только при наличии заключения Правительства РФ.
104 Конституции РФ законопроекты вносятся в ГД субъектами права законодательной инициативы: Президентом РФ, СФ, сенаторами РФ, депутатами ГД, Правительством РФ, законодательными (представительными) органами государственной власти субъектов РФ. Право законодательной инициативы принадлежит также Конституционному Суду РФ, Верховному Суду РФ по вопросам их ведения. Законопроекты о введении или отмене налогов, освобождении от их уплаты, о выпуске государственных займов, об изменении финансовых обязательств государства, др. законопроекты, предусматривающие расходы, покрываемые за счет федерального бюджета, могут быть внесены только при наличии заключения Правительства РФ. Одобренные ГД федеральные конституционные законы и принятые ГД федеральные законы в обязательном порядке в течение 5 дней передаются на рассмотрение СФ.
Одобренные ГД федеральные конституционные законы и принятые ГД федеральные законы в обязательном порядке в течение 5 дней передаются на рассмотрение СФ. 106 Конституции РФ. Их рассмотрение в СФ с учетом п. 1 Постановления Конституционного Суда РФ от 23 марта 1995 «По делу о толковании части 4 статьи 105 и статьи 106 Конституции Российской Федерации» должно начаться не позднее 14 дней после их передачи в СФ. Палата имеет право отклонить федеральный конституционный закон, федеральный закон.
106 Конституции РФ. Их рассмотрение в СФ с учетом п. 1 Постановления Конституционного Суда РФ от 23 марта 1995 «По делу о толковании части 4 статьи 105 и статьи 106 Конституции Российской Федерации» должно начаться не позднее 14 дней после их передачи в СФ. Палата имеет право отклонить федеральный конституционный закон, федеральный закон. Если Президент РФ в течение указанного срока обратится в Конституционный Суд РФ с запросом о проверке конституционности федерального закона, срок для подписания такого закона приостанавливается на время рассмотрения запроса Конституционным Судом РФ. Если Конституционный Суд РФ подтвердит конституционность федерального закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального закона, Президент РФ возвращает его в ГД без подписания.
Если Президент РФ в течение указанного срока обратится в Конституционный Суд РФ с запросом о проверке конституционности федерального закона, срок для подписания такого закона приостанавливается на время рассмотрения запроса Конституционным Судом РФ. Если Конституционный Суд РФ подтвердит конституционность федерального закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального закона, Президент РФ возвращает его в ГД без подписания. Если Конституционный Суд РФ подтвердит конституционность федерального конституционного закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального конституционного закона, Президент РФ возвращает его в ГД без подписания.
Если Конституционный Суд РФ подтвердит конституционность федерального конституционного закона, Президент РФ подписывает его в трехдневный срок с момента вынесения Конституционным Судом РФ соответствующего решения. Если Конституционный Суд РФ не подтвердит конституционности федерального конституционного закона, Президент РФ возвращает его в ГД без подписания. pravo.gov.ru). Подписанный Президентом РФ закон может быть опубликован также в др. печатных изданиях, обнародован по телевидению, радио, передан по каналам связи. Федеральные конституционные законы, федеральные законы вступают в силу одновременно на всей территории РФ по истечении 10 дней после дня их официального опубликования, если самими законами не установлен др. порядок вступления их в силу.
pravo.gov.ru). Подписанный Президентом РФ закон может быть опубликован также в др. печатных изданиях, обнародован по телевидению, радио, передан по каналам связи. Федеральные конституционные законы, федеральные законы вступают в силу одновременно на всей территории РФ по истечении 10 дней после дня их официального опубликования, если самими законами не установлен др. порядок вступления их в силу. Одобренный ГД федеральный конституционный закон, принятый ГД федеральный закон в редакции согласительной комиссии в течение 5 дней направляются на рассмотрение СФ. Если при повторном рассмотрении федерального закона, отклоненного СФ, ГД не приняла его в редакции согласительной комиссии или выразила свое несогласие с решением СФ об отклонении федерального закона, он ставится на голосование в ранее принятой редакции. Решение о принятии федерального закона в ранее принятой редакции принимается большинством не менее двух третей голосов от общего числа депутатов ГД. Принятый ГД федеральный закон в течение 5 дней направляется Президенту РФ для подписания и обнародования. Если решение о принятии федерального закона, отклоненного СФ, в ранее принятой ГД редакции не набрало необходимого для принятия числа голосов, то федеральный закон считается отклоненным и дальнейшему рассмотрению не подлежит. Особенностью рассмотрения федеральных законов, отклоненных Президентом РФ, является возможность создания ГД по предложению Президента РФ либо по согласованию с ним специальной комиссии для преодоления возникших разногласий с предложением СФ направить своих представителей для работы в такой комиссии.
Одобренный ГД федеральный конституционный закон, принятый ГД федеральный закон в редакции согласительной комиссии в течение 5 дней направляются на рассмотрение СФ. Если при повторном рассмотрении федерального закона, отклоненного СФ, ГД не приняла его в редакции согласительной комиссии или выразила свое несогласие с решением СФ об отклонении федерального закона, он ставится на голосование в ранее принятой редакции. Решение о принятии федерального закона в ранее принятой редакции принимается большинством не менее двух третей голосов от общего числа депутатов ГД. Принятый ГД федеральный закон в течение 5 дней направляется Президенту РФ для подписания и обнародования. Если решение о принятии федерального закона, отклоненного СФ, в ранее принятой ГД редакции не набрало необходимого для принятия числа голосов, то федеральный закон считается отклоненным и дальнейшему рассмотрению не подлежит. Особенностью рассмотрения федеральных законов, отклоненных Президентом РФ, является возможность создания ГД по предложению Президента РФ либо по согласованию с ним специальной комиссии для преодоления возникших разногласий с предложением СФ направить своих представителей для работы в такой комиссии. По окончании работы специальная комиссия представляет на повторное рассмотрение ГД федеральный закон в согласованной редакции. Если при повторном рассмотрении ГД федерального закона, отклоненного Президентом РФ, он принят в новой редакции, порядок его рассмотрения в СФ определен как вновь принятого. Если при повторном рассмотрении федеральный закон будет одобрен в ранее принятой редакции большинством не менее двух третей голосов от общего числа сенаторов РФ и депутатов ГД, он подлежит подписанию Президентом РФ в течение 7 дней и обнародованию.
По окончании работы специальная комиссия представляет на повторное рассмотрение ГД федеральный закон в согласованной редакции. Если при повторном рассмотрении ГД федерального закона, отклоненного Президентом РФ, он принят в новой редакции, порядок его рассмотрения в СФ определен как вновь принятого. Если при повторном рассмотрении федеральный закон будет одобрен в ранее принятой редакции большинством не менее двух третей голосов от общего числа сенаторов РФ и депутатов ГД, он подлежит подписанию Президентом РФ в течение 7 дней и обнародованию.


 Так как спин может быть +1/2 или =1/2, есть две комбинации:
Так как спин может быть +1/2 или =1/2, есть две комбинации: Это означает, что при рисовании электронных конфигураций с помощью модели со стрелками вы должны заполнить каждую оболочку одним электроном, прежде чем начинать их спаривание. Помните, что заряд электрона отрицательный и электроны отталкиваются друг от друга. Электроны будут пытаться создать расстояние между ним и другими электронами, оставаясь неспаренными. Это также объясняет, почему спины электронов на орбитали противоположны (то есть +1/2 и -1/2).
Это означает, что при рисовании электронных конфигураций с помощью модели со стрелками вы должны заполнить каждую оболочку одним электроном, прежде чем начинать их спаривание. Помните, что заряд электрона отрицательный и электроны отталкиваются друг от друга. Электроны будут пытаться создать расстояние между ним и другими электронами, оставаясь неспаренными. Это также объясняет, почему спины электронов на орбитали противоположны (то есть +1/2 и -1/2). Если бы частица покоилась, то ее положение и импульс были бы определенными. Поскольку это не так, n должно иметь целочисленное значение. Дело не в том, что главное квантовое число может быть измерено только целыми числами, а в том, что гребень одной волны будет накладываться на впадину другой, и волна гаснет.
Если бы частица покоилась, то ее положение и импульс были бы определенными. Поскольку это не так, n должно иметь целочисленное значение. Дело не в том, что главное квантовое число может быть измерено только целыми числами, а в том, что гребень одной волны будет накладываться на впадину другой, и волна гаснет.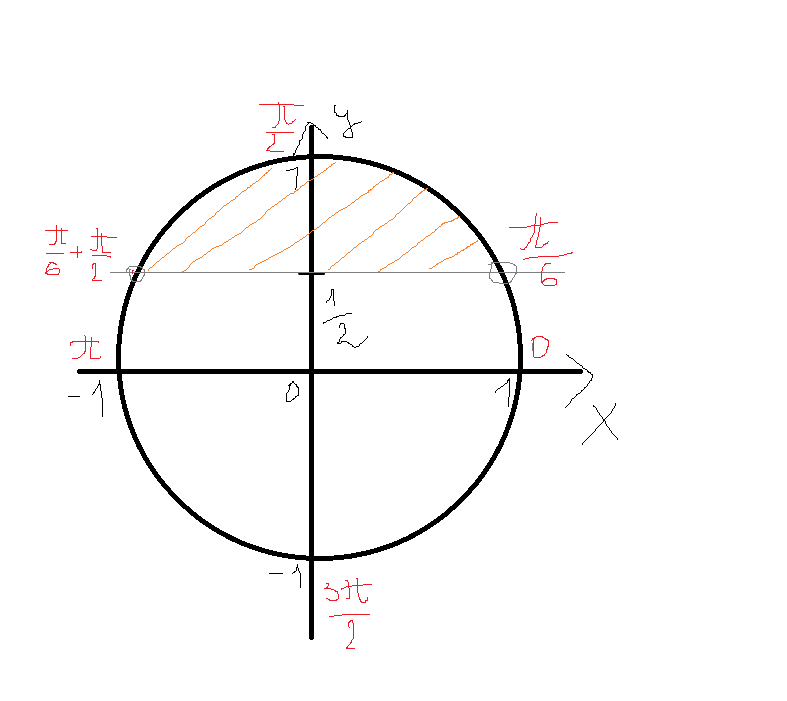 \(m_l=3\) не находится в диапазоне от \(-l\) до \(+l\). Значение должно быть равно -1, 0 или +1.
\(m_l=3\) не находится в диапазоне от \(-l\) до \(+l\). Значение должно быть равно -1, 0 или +1.
 (а/б) н = а н / б н
(а/б) н = а н / б н