Перевернутая f что значит: fkn+antitotal | студентам & программистам — Вебджем.рф

Содержание

ⅎ — Перевёрнутая строчная буква f: U+214E

клавдиева буква

U+214E

Нажмите, чтобы скопировать и вставить символ

Техническая информация

Название в Юникоде	Turned Small F
Номер в Юникоде	U+214E
HTML-код	ⅎ
CSS-код	\214E
Раздел	Буквоподобные символы
Прописная	Ⅎ
Версия Юникода:	5. 0 (2006)

Значение символа

Перевёрнутая строчная буква f. Буквоподобные символы.

Символ «Перевёрнутая строчная буква f» был утвержден как часть Юникода версии 5.0 в 2006 г.

Свойства

Версия	5.0
Блок	Буквоподобные символы
Тип парной зеркальной скобки (bidi)	Нет
Композиционное исключение	Нет
Изменение регистра	214E
Простое изменение регистра	214E

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	E2 85 8E	226 133 142	14845326	11100010 10000101 10001110
UTF-16BE	21 4E	33 78	8526	00100001 01001110
UTF-16LE	4E 21	78 33	20001	01001110 00100001
UTF-32BE	00 00 21 4E	0 0 33 78	8526	00000000 00000000 00100001 01001110
UTF-32LE	4E 21 00 00	78 33 0 0	1310785536	01001110 00100001 00000000 00000000

Наборы с этим символом:

Ⓐ
Символы для ников

Что значит перевернутая буква А?

Строчная ɐ используется в международном фонетическом алфавите для обозначения ненапряжённого неогублённого гласного среднего ряда нижнего подъёма. Эта буква была использована в XVIII веке Эдвардом Ллуйдом и Вильямом Прайсом в качестве фонетического символа для корнского языка.

Что значит перевернутая буква А в математике?

Символ ∀ (перевёрнутая А) и ∃ (Е наоборот) — всего-навсего английские «Any» и «Exist», попавшие в «математический международный» таким идиотским способом из-за уже используемых «А» (альфа) и «Е» (число Эйлера). То есть: Символ ∀ (Any) используется для обозначения фразы «Для любого…», «Для любых…».

Что за знак перевернутая э?

Ответ, проверенный экспертом Знак ∈ означает что принадлежит, а знак ∉ означает что не принадлежит.

В каком языке есть перевернутая е?

Перевёрнутая E. Ǝ — письмо расширенного латинского алфавита. использован панегирические алфавит, где 8-й буквы алфавита. буквы также включены в африканском ссылкой алфавита, где 14-й письмо.

Как написать перевернутую букву Е?

Ǝ — Латинская заглавная буква перевернутая «E»: U+018E — Таблица символов Юникода

Что означает буква Е?

Метка «E» рядом с треками или музыкальными релизами обозначает, что в материале содержится так называемый «Explicit content», что обычно выражается в наличии лексики, которая может быть расценена как ненормативная или нежелательная по иным причинам, в текстах песен. » («…умножить на десять в степени…»), p — порядок. Это необходимо для представлении очень больших и очень малых чисел, а также для унификации их написания.

Что значит буква Т в музыке?

Такт — непрерывно повторяющаяся часть метра от одного сильнейшего ударения до следующего ударения равной с ним силы. Тактовая черта — вертикальная линия, перерезающая нотный стан и отделяющая один такт от другого. …

Что значит буква Т в ВК музыке?

Знак «Т» — Текст/Text показан только в тёмной компьютерной версии. Означает, что в треке присутствует дополнение, слова, помеченные при редактировании композиции.

Что означает буква Т в физике?

T, t — в физике: Обозначение времени Обозначение температуры

Что означает черта над нотой?

В нотах обозначается маленькой горизонтальной черточкой под или над нотой. Маркато (итал. marcato «выделяя, подчеркивая») штрих более жесткий, чем legato. Обозначает подчеркнутое, отчетливое исполнение каждого звука, которое достигается посредством акцента.

Что означает волнистая линия в нотах?

Волнистая линия после tr ставится либо для длинных трелей, либо в тех случаях, когда трель применяется к нескольким (или слигованным) нотам. Эти обозначения ставятся над главной (гармонической) нотой. … В современной нотации одиночная волнистая линия без tr над нотой обозначает вибрато.

Что значит слово легато?

В нотной записи легато обозначается дугообразной линией — лигой, объединяющей ноты, исполняемые легато. Также может обозначаться словом legato около соответствующей группы нот. Легато, как стаккато, является своего рода артикуляцией.

Что означает крестик рядом с нотой?

Крестик называется дубль-диез (два диеза). Он действует на один такт и повышает ноту не на полтона, а на целый тон. Фа-дубль-диез — это соль. Комбинация бекар-диез означает, что один из этих двух диезов отменен, а другой остался.

Что означает бемоль в начале?

Звук «чёрной клавиши» ниже ноты ре на полтона. Понижение основной ступени на полтона называют словом бемоль. … В начале статьи мы акцентировали внимание на том, что одна и та же клавиша (чёрная) находится правее клавиши с нотой «до» и одновременно левее клавиши с нотой «ре».

Что такое Диезы и Бемоли?

Основные знаки альтерации — диез, бемоль и бекар. Диез повышает звук на полтона, бемоль понижает звук на полтона, а бекар отменяет действие диеза и бемоля.

Что означают цифры на нотном стане?

Размер всегда обозначается дробью: числитель – количество длительности в такте (об этом понятии подробнее ниже), знаменатель – указание длительности. Обычно размер ставится один раз за все произведение и находится после ключа и ключевых знаков (о ключевых знаках подробнее ниже).

Как в нотах обозначается педаль?

В нотах эта педаль обозначается буквой P (или сокращением Ped.), а её снятие — звёздочкой. В музыке композиторов эпох романтизма и импрессионизма часто встречаются эти обозначения, обычно для придания звуку особого колорита. Левая педаль используется для ослабления звучания.

Что означает буква С в нотах?

Первоначально для записи нот использовали греческий алфавит, позже стали записывать ноты латинскими буквами. … Вот, какие буквы соответствуют основным семи звукам: c [цэ] – до; d [дэ] – ре; e [э] – ми; f [эф] – фа; g [гэ] – соль; a [а] – ля; h [ха] – си.

Чем разделяется нотная запись?

Для удобства чтения нот музыкальная запись делится на равные отрезки времени (количество ударов) – такты. Такт – это отрезок нотной записи, ограниченный двумя тактовыми чертами. Первая нота каждого такта имеет ударение — акцент. Эта акцентируемая доля служит началом счета в каждом такте.

Что такое символы и знаки в музыке?

Справка: Музыкальные символы . Музыкальные символы — это знаки и символы в нотной записи, которые указывают на различные аспекты исполнения музыкального произведения.

Что такое символ в музыке?

Символ является той связью, которая объединяет духовное с чувственным, абстрактное с конкретным. В наше время пласт культуры эпохи барокко оказался в значительной степени забытым, подобные ассоциации у большинства уже не возникают. Его возрождение открывает новые возможности для постижения инструментальной музыки И.

Что означают музыкальные ноты?

Но́та (лат. nōta — «знак», «метка») в музыке — графическое обозначение звука музыкального произведения, один из основных символов современной музыкальной нотации.

Почему ноты называются именно так?

С легкой руки Гвидо д’Ареццо начальные слоги каждой строчки и стали названиями нот: ut, re, mi, fa, sol, la. В конце концов ноту ut пришлось заменить на всем известную do из-за неудобства пения открытого звука в первом слоге. Считается, что ее название пошло от латинского Dominus, что значит «Господь».

Как переводится До ре ми фа соль ля си?

В переводе означает: «Чтобы в полный голос смогли воспеть рабы твоих деяний чудеса, сними грех с их уст, Святой Иоанн».

Почему ноты начинаются с C?

По первым слогам строчек назвали ноты. В гимне первой была До. Буквы при этом менять не стали, чтобы не запутать всех еще больше — хватает и вечной головной боли с В, которая теперь то ли Си, то ли Си-бемоль, то ли черт его вообще разберет.

Почему в средние века первая нота имела другое название?

Именно Ареццо придумал названия нот. Он обозначил их первыми слогами слов молитвы к Иоанну Крестителю. Эту мелодию в церковном хоре использовали в качестве распевки. В молитве звучит просьба о сохранении силы голоса.

Откуда взялись ноты?

Итальянский монах, музыкант и учитель пения Гвидо Аретинский — Гвидо д’ Ареццо нарисовал линии, на которых разместились ноты. Изобретатель современной системы нотной записи – бенедиктинский монах Гвидо Аретинский (Гвидо д’Ареццо) (990-1050). Ареццо – небольшой городок в Тоскане, неподалеку от Флоренции.

Кто придумал До ре ми фа соль ля си?

монах Гвидо

Что такое методика перевернутого класса, кто ее автор и в чем суть модели обучения в перевернутом классе

Суть модели обучения перевёрнутого класса

Название «перевёрнутый класс», или flipped classroom, выбрано не случайно — подразумевается, что здесь всё не так, как на обычном уроке. Согласно этой концепции, школьники изучают теорию дома, перед занятием. А на самом уроке отрабатывают её на практике под руководством педагога.

Методику в 2007 году придумали Джонатан Бергман и Аарон Сэмс — преподаватели химии в американской школе. Позже её начали использовать и другие учителя–предметники.

Зачем нужен перевёрнутый класс

В обычных классах много недостатков. Вот несколько примеров.

‍Если ученик не понял что-то из теории, сложно это наверстать. На уроке педагог торопится изложить материал так, чтобы успеть всё. Часто этого не хватает на полноценное объяснение темы, а ребёнок не успевает за темпом объяснений учителя. Или время уходит на организационные вопросы и разборки по поводу дисциплины, а до новой темы доходит только под конец занятия. Ученики уходят домой с кучей вопросов — им приходится звать родителей, подключать репетиторов и пытаться понять, в чём суть материала и домашнего задания.

Решение, которое предлагает перевёрнутый класс: теория подаётся до урока, и ученик может потратить на её изучение столько времени, сколько потребуется — хоть пять раз пересмотреть лекцию и сделать несколько конспектов. Так усваивать материал легче.

‍На практику просто не хватает времени. А она важнее, чем теория. Можно провести аналогию с любой профессией: для хирурга имеет значение не количество прочитанных научных трудов, а количество успешно проведённых операций.

Решение, которое предлагает перевёрнутый класс: каждый урок посвящается практике. У школьников не возникает вопросов, как решать задачки в домашке, потому что каждая разбирается вместе с учителем в классе. Итог — ученики способны применять знания на практике.

Часто уроки построены однообразно. Учёба идёт по надоевшему кругу: учитель разжевал тему, дома ребёнок попытался решить домашку, осталось куча вопросов, кому задать — непонятно. Новые форматы и интерактив подключаются редко.

<<Форма демодоступа>>

Решение, которое предлагает перевёрнутый класс: разнообразие форматов и видов деятельности. Теория может подаваться в форме параграфов, статей, видеоматериалов, презентаций, ссылок на нужные учебники. Некоторые педагоги записывают собственные видеолекции и отправляют ученикам в качестве теории, чтобы те разобрали тему дома и пришли на урок подготовленные.

Другие учителя, напротив, считают, что дети должны сами учиться искать информацию и обрабатывать её, и не дают конкретных материалов для изучения, а только называют тему. Тогда задача школьника — самостоятельно найти теоретический материал и прийти на занятие перевёрнутого класса.

Практика может проходить в формате викторин, игр, мастер-классов, проектов, дискуссий, симуляций, разбора задач и кейсов, опытов и экспериментов.

Пока что недостаточно исследований о том, насколько эффективно перевёрнутый класс решает проблемы. Но педагоги, которые уже работают по новой системе, отмечают, что ученики показывают достойные академические результаты.

<<Форма с консультацией>>

Преимущества и недостатки перевёрнутого класса

Вот несколько плюсов и минусов этой необычной системы.

Плюсы

✅ Школьники изучают материал в удобном темпе. Перевёрнутый класс позволяет потратить на изучение темы ровно столько времени, сколько нужно для понимания. Ученик в любой момент может поставить запись лекции на паузу или перемотать назад.
✅ Перевёрнутый класс развивает самостоятельность и умение докапываться до сути.
✅ Школьники больше приспособлены к решению практических задач, чем к теоретическим положениям. Они чётко знают, как применять знания на практике.
✅ Если пропустить урок в перевёрнутом классе, всё равно получишь знания, изучив дома теорию.

Минусы

❌ «Задано устно — значит не задано». Если ребёнок не слишком знаком с концепцией перевёрнутого класса, ему может быть непривычно перестроиться.
❌ Концепция подразумевает, что нужно действительно готовиться к уроку. Нельзя просто прийти на урок и ждать, что тебе всё объяснят.
❌ Нельзя оперативно задать вопросы лектору, когда смотришь лекцию дома.

Резюме

Модель урока перевёрнутого класса пока не прижилась на постоянной основе ни на западе, ни в России.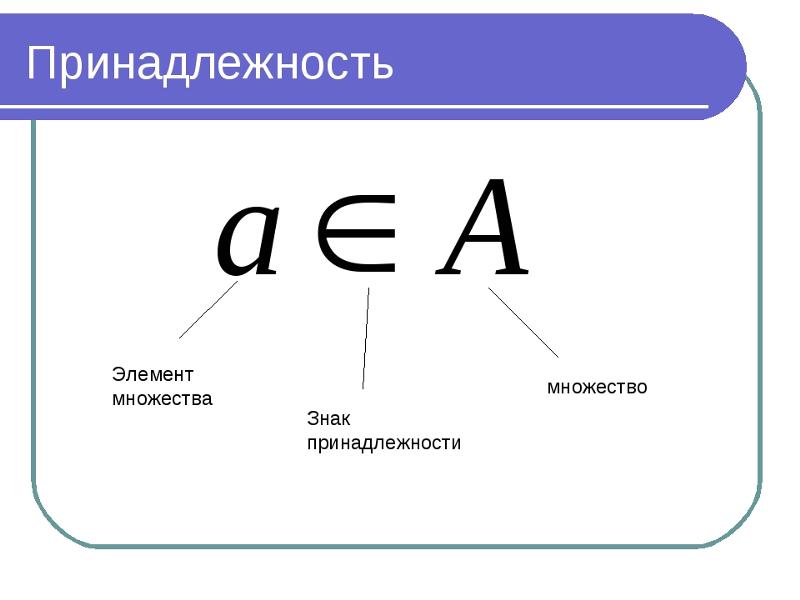 Но есть экспериментальные классы, где учителя работают по такой системе. Каждый сам решает, как лучше организовать учёбу.

Считается, что такая методика компенсирует недостатки традиционной образовательной системы: в частности, нехватку времени на объяснение теории и неумение школьников применять знания на практике.

Успех перевёрнутой методики зависит от синергии между преподавателем и учениками и требует постоянной мотивации до, во время и после обучения. Вряд ли эта концепция станет повсеместной в ближайшие годы — но уже становится популярной.

Антенны: перевернутая F-антенна (IFA)

Основы IFA

Перевернутая F-антенна показана на рисунке 1. Хотя эта антенна выглядит как проволочная антенна, после некоторого анализа того, как эта антенна излучает, ее точнее классифицировать как апертурную антенну.

Рис. 1. Геометрия перевернутой F-антенны (IFA).

Подача размещается от плоскости земли до верхнего плеча ИФА. Верхнее плечо ИФА имеет длину это примерно четверть длины волны. Слева от подачи (как показано на рис. 1) верхний рычаг замыкается на землю. Подача ближе к закорачивающему штифту, чем к открытому концу плеча. Поляризация этой антенны вертикальная, а диаграмма направленности имеет примерно форму пончика с осью пончика в вертикальном направлении. Заземляющая плоскость должна быть не меньше длины IFA (L), а заземляющая высота плоскости должна быть не менее лямбда/4. Если высота заземляющего слоя меньше, полоса пропускания и эффективность снизится. Высота IFA (H) должна составлять небольшую долю длины волны. Свойства излучения и импеданс не сильно зависят от этого параметра (H).

Поскольку структура несколько напоминает перевернутую F, эта антенна получила название «перевернутая F-антенна».

Анализ

Почему эта структура излучает? Вернемся и посмотрим на щелевая антенна, показана на рисунке 2.

Рис. 2. Геометрия щелевой антенны.

Щелевая антенна должна иметь длину в половину длины волны для надлежащего излучения (в более общем случае, длина периметра щелевой антенны должна составлять примерно одну длину волны). Как это на антенну подается (или возбуждается источником напряжения) напряжение на концах щели (поперек апертуры) должен быть равен нулю из-за закорачивающих контактов с обеих сторон. Если на краях щели напряжение равно нулю, то напряжение будет максимальным на расстоянии четверти волны (в центре щели).

А где максимальный ток? Поскольку эту антенну также можно рассматривать как линия передачи, источник в основном «видит» короткозамкнутую линию передачи в любом направлении. Мы Из теории линий передачи известно, что при коротком замыкании линии передачи напряжение и ток сдвинуты по фазе на 90 градусов. В результате ток будет ноль в центре щелевой антенны и будет максимальным по краям. Напряжение а распределение тока показано на рисунке 3 (обратите внимание, что пиковое напряжение принимается равным P вольтам, и пиковый ток А Ампер).

Рис. 3. Распределение напряжения и тока вдоль полуволновой щелевой антенны.

Щелевая антенна излучает, потому что напряжение находится в фазе по всему апертуры, так что электронное поле является вертикальным и выстраивается вдоль всей щели. Это также приводит к вертикальной поляризации.

Как это связано с IFA? Вот ключевой момент: если текущий в центре щели равен нулю (как показано на рис. 3), то щелевая антенна можно рассматривать как наличие разомкнутой цепи в центре слота. Следовательно, если мы ломаем прорезь пополам, и избавляемся от правой стороны, у нас остается ИФА антенна, как показано на рис. 1.

Обратите внимание, что ИФА может поддерживать точно такой же режим излучения. То есть, поскольку ИФА имеет обрыв с правой стороны подачи (рис. 1), ток будет ноль в этой точке и напряжение будет максимальным — ровно как в щелевой антенне кейс. Следовательно, IFA можно рассматривать как «половину щелевой антенны». И действительно, это актуальная модель антенны. Следовательно, IFA классифицируется как апертурная антенна, даже хотя диафрагма не «закрыта».

Модель схемы для антенн IFA (и Slot)

Для эффективного излучения нам нужно, чтобы антенна была хорошей излучающей структурой (т. токи или электрические поля складываются по фазе), и нам нужно иметь возможность получить энергию по линии передачи и на антенну. Это означает, что нам нужен импеданс антенны должно быть примерно 50 Ом (обычно). Для этого желательно чтобы реактивная составляющая импеданса (мнимая часть) была равна нулю. Для МФА или щелевая антенна, обратите внимание, что канал видит короткозамкнутую линию передачи на небольшую долю длины волны от антенны. Закороченная линия передачи, которая представляет собой небольшую часть длины волны. создает индуктивную реактивную составляющую. Точно так же разомкнутая цепь на IFA создает емкость справа от подачи. Место подачи выбрано так, чтобы «сбалансировать» емкость (справа от подачи). и индуктивность (слева от подачи, как показано на рисунке 1). Индуктивность и емкость компенсируют вне, оставив только радиационную стойкость. Эквивалентная модель схемы IFA показан на рис. 4.

Рис. 4. Модель схемы для антенны IFA.

Обратите внимание, что для щелевой антенны на рис. 2 короткое замыкание справа от облучателя по-прежнему создает помехи. емкость, потому что длина щели справа от подачи больше четверти длины волны.

Что касается реальной части импеданса для IFA или щелевой антенны, обратите внимание, что если щелевая антенна питался в центре щели (где напряжение максимально, а ток равен нулю — Z=V/I), импеданс был бы практически бесконечным, так что антенна не излучала бы. Отодвигая подачу от центра для слота это также позволяет току уменьшаться от нуля, что позволяет падать импедансу до более желательного значения. То же самое верно и для антенны IFA. Следовательно, место подачи критический фактор при разработке IFA или слота.

Хорошее место для корма может быть легко получено экспериментально при проектировании антенны.

Примеры IFA в реальном мире

IFA обычно используются в мобильных телефонах из-за их небольшого размера (четверть длины волны). Пример нескольких IFA в мобильном телефоне можно четко увидеть на Palm Pre. Эти антенны видны после снятия задней крышки, как показано на рис. 5:

Рис. 5. Антенны Palm Pre можно увидеть, сняв заднюю крышку.

Желтая полоска на левой стороне антенны Palm — это антенна GPS, которая представляет собой IFA. С частота GPS составляет 1,575 ГГц, четверть длины волны составляет около 1,87 дюйма (4,75 см). это примерно длина ИФА в реальном изделии (укорочена для правильной настройки).

Две другие антенны видны на Рисунке 5. В правом верхнем углу находится антенна ячейки разнесения, которая является приемной антенной (не передает). В нижней части устройства находится двухдиапазонный IFA. Эта антенна является приемо-передающей. сотовая антенна, которая должна работать в диапазонах 900 МГц и 1800 МГц. Для этого антенные инженеры сделал IFA для диапазона высоких частот (1800 МГц), который является более коротким плечом, показанным на рисунке 5. Используя тот же питания и закорачивающего штифта, они отходят от другого плеча для нижней полосы (более длинное плечо, которое обернуто несколько вокруг себя). Поскольку у дизайнеров было ограниченное пространство (что является большой проблемой в антенны мобильного телефона), они обернули IFA вокруг себя по краям. Делая это, они были в состоянии получить необходимую длину для 900 МГц ИФА. Однако, обернув антенну вокруг себя, в пропускная способность и радиационная эффективность снижаться.

Таким образом, антенна IFA удобна из-за ее небольшого размера и простой конструкции. В следующий В разделе мы рассмотрим щелевые волноводные антенны.

Видео: анализ антенны IFA

В качестве дополнения к этой странице здесь представлено видеообсуждение IFA. Многие из концепций одинаковы, но материал подается по-разному:

1.7 — Обратные функции

Обозначение

Обратная функция f обозначается как f ^-1 (если ваш браузер не поддерживает верхние индексы, то это выглядит как f с показателем -1) и произносится как «f inverse». Хотя обратная функция выглядит как вы возводите функцию в степень -1, это не так. Обратная функция не означает, что обратная функция.

Инверсия

Функция обычно говорит вам, что такое y, если вы знаете, что такое x. Обратная функция расскажет каким должен быть x, чтобы получить это значение y.

Функция f ^-1 обратна f, если

для каждого x в области f, f ^-1 [f(x)] = x и
для каждого x в области f ^-1 , f[f ^-1 (x)] = x

Домен f — это диапазон f ^-1, а диапазон f — это домен f ^-1 .

График обратной функции

Обратная функция отличается от функции тем, что все координаты x и координаты y были переключены. То есть, если (4,6) — точка на графике функции, то (6,4) — точка на график обратной функции.

Точки на функции идентификации (y=x) останутся на функции идентификации при переключении. Все у других точек будут изменены координаты и места перемещения.

График функции и функция, обратная ей, являются зеркальным отражением друг друга. Они отражаются о тождественная функция y=x.

Существование обратной функции

Функция говорит, что для каждого x существует ровно один y. То есть значения y могут дублироваться, но x значения не могут повторяться.

Если функция имеет обратную, которая также является функцией, то для каждого x может быть только один y.

Функция взаимно однозначного — это функция, в которой для каждого x имеется ровно один y и для каждого y, есть ровно один х. У взаимно однозначной функции есть обратная, которая также является функцией.

Существуют функции, обратные функции которых не являются функциями. Есть также обратные для связи. По большей части мы ими пренебрегаем и имеем дело только с функциями, обратные также функционирует.

Если обратная функция также является функцией, то обратная связь должна проходить через вертикальную линию тест. Поскольку все координаты x и y меняются местами при нахождении инверсии, говоря что обратная функция должна пройти тест вертикальной линии, это то же самое, что сказать, что исходная функция должна пройти тест тест горизонтальной линии.

Если функция проходит как тест вертикальной линии (так что это в первую очередь функция), так и тест горизонтальной линии (чтобы его обратная функция была), то функция является взаимно однозначной и имеет обратная функция.

Неформальное нахождение инверсий

Инверсия некоторых функций, особенно тех, где есть только одно вхождение независимая переменная, может быть решена путем отмены операций. Чтобы отменить операцию, вы должны не только изменить порядок, но и использовать обратную операцию.

Пример 1

Функция f(x) = 5x-2

Начать с х: х
Умножить на 5: 5x
Вычесть 2: 5x-2

Обратная f

^-1 (x) = (x+2)/5

Начать с х: х
Добавить 2: х+2
Разделить на 5: (х+2) / 5

Пример 2

Функция f(x) = 2(x-3)

² -5, x≥3

Обратите внимание, что существует ограничение на x.

Начать с х: х
Вычесть 3: x-3
Квадрат: (x-3) ²
Умножить на 2: 2(x-3) ²
Вычесть 5: 2(x-3) ² -5

Обратная f

^-1 (x) = 3 + sqrt[(x+5)/2]

Начать с х: х
Добавить 5: х+5
Разделить на 2: (х+5)/2
Извлеките квадратный корень: ± sqrt[(x+5)/2]
Добавить 3: 3 ± sqrt[(x+5)/2]
Подождите! Эта обратная функция не является функцией, потому что для каждого x существует два значения y. Это из-за ±, который появился, когда мы взяли квадратный корень из обеих сторон. Теперь вернемся к исходной области определения x≥3. Это означает, что для инверсии диапазон равен y≥3. Поскольку у должно быть не менее 3, нам нужен положительный квадратный корень, а не отрицательный. Без ограничения на x в исходная функция, у него не было бы обратная функция: 3 + sqrt[(x+5)/2]

Пример 3

Функция f(x) = x

² — 4x + 6, x≤2

Уххх????

Что происходит, когда встречается более одного независимая переменная в функции? Вы не знаю, что ты сделал с х, потому что ты сделал это с двумя разные иксы, и вы не сделали то же самое с обоими из их.

Формальное нахождение инверсий

Нельзя сказать, что последний пример невозможно выполнить, но он включает в себя заполнение квадрата до получить f(x) = (x-2) ² +2, затем инвертируйте его, чтобы получить f ^-1 (x) = 2-sqrt(x-2).

Тем не менее, есть другой способ, который не так сильно зависит от неформальности и будет работать независимо от того, не вы можете точно понять, что вы сделали с ровно одним x.

Запуск с функцией
При необходимости заменить f(x) на y
Поменяйте местами x и y. На данный момент вы имеете дело с обратным
Найти у
Заменить у на f ^-1 (x), если обратная функция также является функцией, в противном случае оставьте значение y

Пример 4

Функция f(x) = x

² / (x ² +1), x≥0

Важно сделать ограничение 1-1.

Начните с функции: f(x) = x ² / (x ² +1), x≥0
Заменить f(x) на y: y = x ² / (x ² +1), x≥0
Поменяйте местами x и y: x = y ² / (y ² +1), у ≥0
Найдите у:
1. Умножить на знаменатель: x(y ² +1) = y ²
2. Распределить: xy ² + x = y ²
3. Переместить y в одну сторону, а все остальное в другую: xy ² -y ² = -x
4. Коэффициент: у ² (х-1)=-х
5. Разделить на коэффициент при y ² : y ² = -x/(x-1)
6. Упростить правую часть: y ² = х/(1-х)
7. Извлечение квадратного корня: y = ± sqrt[ x/(1-x) ]
8. Поскольку y≥0, нам нужен положительный квадратный корень: y = sqrt[ x/(1-x) ]
Назовите это f ^-1 (x): f ^-1 (x) = sqrt[ x/(1-x) ]

Для этой последней функции подразумеваемый домен обратной функции равен [0,1). Это означает, что диапазон исходная функция также должна была быть [0,1). Проверьте это на своем калькуляторе, и вы увидите, что это так.

Иногда в инструкциях говорят, что если функция не является взаимно однозначной, то не найти обратную функция (потому что ее нет). Поэтому всегда проверяйте, прежде чем тратить время на поиски обратная функция. Теперь, если вы должны найти обратное, независимо от того, является ли оно работать или нет, тогда вперед.

Хороший материал!

Один к одному Функции — замечательная штука.

При решении уравнений можно прибавлять одно и то же к обеим частям, вычитать одно и то же из обе стороны, умножить обе стороны на одно и то же ненулевое значение и разделить обе части на одно и то же ненулевое значение и по-прежнему получать то же решение, не беспокоясь о необходимости проверить свой ответ.

Вы также можете применить функцию «один к одному» к обеим частям уравнения, не беспокоясь о введении посторонних решений (решений, которые работают после выполнения чего-то, что раньше не работало). Это не обязательно верно для функций, которые не являются взаимно однозначными, как функция возведения в квадрат, где вы всегда должны проверять ответы после возведения в квадрат обеих частей уравнения. Например, уравнение sqrt(x) = -2 не имеет решения, но если вы возведете в квадрат обе стороны, вы получите x = 4, но это не проверяется исходной задачей. Благодаря функциям «один к одному» вы не будете внедрять никаких посторонних решений.

Вау! Говорить о мощный. Вы не оцените это сейчас, и книга не рассматривает это должным образом, пока вы не получите к главе 4 и имеют дело с логарифмическими и экспоненциальными функциями, и даже тогда они не делают как бы это ни было важно.

Хорошо, давайте попробуем. Поверьте мне на слово, что exp(x) является взаимно однозначной функцией и обратный ln(x).

ln(x) = 3: Найдите x.
ехр[ln(x)] = ехр[3]

Ничего себе — больше сплоченности. Обратную функцию можно найти, взяв функцию [2 ^nd ]. Смотреть у него для прочего на калькуляторе.

Квадратный корень является обратным значением квадрата. Если вы посмотрите на три тригонометрических ключа [sin], [cos] и [tan], их обратные значения находятся с помощью клавиши [2 ^nd ].

Режим Soapbox включен.

Говорю вам — все сходится. Для тех, кто помнит реплику Ганнибала Смита в A-Team: «Мне нравится, когда складывается план».

Математика — один из самых популярных предметов. Все дополняет все еще. Я надеюсь, что вы вынесете из этого курса гораздо больше, чем просто механику математике, а понимание, понимание и понимание того, как работает система. С таким прочным фундаментом математика может быть менее напряженной и даже приятной. У вас есть перестать иметь дело с концептами как с отдельными вещами, которые не связаны друг с другом и самостоятельны. Все они связаны друг с другом и переплетены. Их нельзя разделить и понять.

Режим Soapbox выключен.

Обратные функции

Обратная функция работает в обратном направлении!

Начнем с примера:

Здесь у нас есть функция f(x) = 2x+3 , записанная в виде блок-схемы:

Обратная функция идет другим путем:

Таким образом, инверсия: 2x+3 равна: (y-3)/2

Инверсию обычно показывают, добавляя маленькую «-1» после имени функции, например:

f ^-1 (y)

Мы говорим « f обратное y»

Итак, обратное выражение f(x) = 2x+3 записывается:

f ^{-1 y) = (y-3)/2}

(я также использовал y вместо x , чтобы показать, что мы используем другое значение). заключается в том, что она должна вернуть нам исходное значение:

Когда функция f превращает яблоко в банан,
Тогда обратная функция f ^-1 превращает банан обратно в яблоко

Пример:

Используя приведенные выше формулы, мы можем начать с x=4:

f(4) = 2×4 +3 = 11

Затем мы можем использовать обратное число 11:

f ^-1 (11) = (11-3)/2 = 4

И мы волшебным образом снова получаем 4 !

Мы можем записать это в одну строку:

f ^-1 ( f(4) ) = 4

«f обратное число f из 4 равно 4»

Таким образом, применение функции f, а затем обратной функции f ^-1 снова дает нам исходное значение:

f ^-1 ( f(x) ) = x

другой порядок, и он все еще работает:

f( f ^-1 (x)) = x

Пример:

Начните с:

f ^-1 (11) = (11-3)/2 = 4

И тогда:

f(4) = 2×4+3 = 11

Итак, мы можем сказать:

f( f ^-1 (11) ) = 11

«f от f обратное 11 равно 11»

Решить с помощью алгебры

Мы можем решить обратное с помощью алгебры. Подставьте «y» вместо «f(x)» и решите для x:

Функция:	ф(х)	=	2x+3
Поместите «y» вместо «f(x)»:	г	=	2x+3
Вычесть 3 с обеих сторон:	у-3	=	2x
Разделить обе стороны на 2:	(у-3)/2	=	х
Поменять стороны:	х	=	(у-3)/2

Решение (поместите «f ^-1 (y)» вместо «x»):	ф ^-1 (у)	=	(у-3)/2

Этот метод хорошо работает для более сложных инверсий.

Фаренгейты в Цельсии

Полезным примером является преобразование Фаренгейтов в Цельсий:

Чтобы преобразовать Фаренгейты в Цельсии: f(F) = (F — 32) × 5 9

94 Обратное 9 (обратно по Цельсию в градусы Фаренгейта): f ^-1 (C) = (C × 9 5 ) + 32

Для вас: посмотрите, сможете ли вы выполнить шаги для создания этой инверсии!

Обратные общие функции

До сих пор это было легко, потому что мы знаем, что обратная функция умножения — это деление, а обратная функция сложения — вычитание, но как насчет других функций?

Вот список, который вам поможет:

Инверсия			Осторожно!
	<=>
	<=>		Не делить на ноль
1 х	<=>	1 г	x и y не равны нулю
x ²	<=>		х и у ≥ 0
x ^нет	<=>	или	n не ноль (разные правила когда n нечетное, четное, отрицательное или положительное)
е ^х	<=>	п(у)	г > 0
а ^х	<=>	журнал _a (у)	г и а > 0
грех(х)	<=>	грех ^-1 (у)	от -π/2 до +π/2
кос(х)	<=>	cos ^-1 (у)	от 0 до π
желто-коричневый(х)	<=>	рыжевато-коричневый ^-1 (у)	от -π/2 до +π/2

(Примечание: вы можете прочитать больше об арксинусе, косинусе и тангенсе. )

Осторожно!

Вы видели «Осторожно!» колонка выше? Это потому, что некоторые инверсии работают только с определенными значениями .

Пример: Возведение в квадрат и квадратный корень

Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, получается следующее:

Квадрат:(−2) ² = 4

Обратное (квадратный корень): √(4) = 2

Но мы не вернули исходное значение! Мы получили 2 вместо −2 . Наша вина, что мы не были осторожны!

Таким образом, функция квадрата (в ее нынешнем виде) не имеет обратной

Но мы можем это исправить!

Ограничить домен (значения, которые могут быть переданы в функцию).

Пример: (продолжение)

Только убедитесь, что мы не используем отрицательные числа.

Другими словами, ограничьте его до x ≥ 0 , и тогда мы получим обратное.

Итак, у нас есть такая ситуация:

x ² имеет ли , а не обратное
но {х ² | x ≥ 0 } (что говорит «x в квадрате, так что x больше или равен нулю», используя нотацию построителя наборов) имеет ли инверсию.

Нет обратного?

Давайте графически посмотрим, что здесь происходит:

Чтобы получить обратное значение, нам нужно уникальных значения .

Только подумайте… если есть два или более x-значения для одного y-значения , как мы узнаем, какое из них выбрать при возвращении?

Общие функции

Нет обратного

Представьте, что мы пришли из x ₁ к определенному значению y, куда мы вернемся? х ₁ или х ₂ ?

В этом случае у нас не может быть обратного.

Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.

Это называется «однозначным соответствием» или биективной функцией, например,

биективной функцией

Имеет обратный

Функция должна быть «биективной», чтобы иметь обратную.

Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.

Домен и диапазон

Так о чем все эти разговоры о « Ограничение домена «?

В своей простейшей форме домен — это все значения, которые входят в функцию (а диапазон — это все значения, которые выходят).

В нынешнем виде приведенная выше функция имеет обратную функцию , а не , потому что некоторые значения y будут иметь более одного значения x.

Но мы могли бы ограничить домен, чтобы было уникальный x для каждого y …

… и теперь мы можем иметь обратную:

Обратите также внимание:

Функция f(x) переходит от домена к диапазону ,
Обратная функция f ^-1 (y) переходит из диапазона обратно в домен.

Давайте изобразим их обоих с точки зрения x . .. так что теперь f ^-1 (x) , а не f ^-1 (y) :

f(x) и f ^-1 (x) подобны зеркальным отражениям
(перевернуто по диагонали).

Другими словами:

График f(x) и f ^-1 (x) симметричен относительно прямой y=x

Квадрат

Пример:

)

Сначала , мы ограничиваем домен до x ≥ 0 :

{x ² | x ≥ 0 } «x в квадрате так, что x больше или равен нулю»
{√x | x ≥ 0 } «квадратный корень из x такой, что x больше или равен нулю»

И вы можете видеть, что они «зеркальные изображения»
относительно диагонали y=x.

Примечание: когда мы ограничиваем домен до x ≤ 0 (меньше или равно 0), обратное значение равно f ^-1 (x) = −√x :

{x ² | х ≤ 0 }
{−√x | х ≥ 0 }

Которые тоже обратные.