на клавиатуре, в окне программы
На компьютерной клавиатуре, помимо букв алфавита и цифр, также представлены самые популярные символы, которые чаще всего используются в программах при работе с текстовой и другой информацией, в том числе, знаки сравнения – “больше” и “меньше”. Но что делать, если требуется вставить символ “не равно”, который физически не представлен на устройстве ввода? Давайте посмотрим, как можно справиться с этой задачей в Эксель.
Примечание: В Excel “не равно” используется в двух вариантах:
- “<>” – в формулах и функциях;
- “≠” – для визуализации информации.
Знак “<>”
Данный знак используется для задания логического условия в формулах и аргументах функций. Также некоторые пользователи даже при визуальном отображении информации предпочитают использовать этот символ вместо “≠”.
Т.к. оба символа (“<“ и “>”), из которых состоит знак, представлены на клавиатуре, все что требуется, чтобы напечатать их – нажать соответствующие клавиши вместе с зажатым  Обратите внимание на раскладку клавиатуры (должна быть английская), в случае неверного выбора будут напечатаны заглавные буквы “Б” и “Ю”.
Обратите внимание на раскладку клавиатуры (должна быть английская), в случае неверного выбора будут напечатаны заглавные буквы “Б” и “Ю”.
Если вдруг клавиатура перестала работать (например, сели батарейки), и срочно требуется набрать знак, можно выполнить следующие действия:
- Встаем в ячейку, в которую хотим вставить символ. Переключаемся во вкладку “Вставка” и щелкаем по пункту “Символы” в левом углу ленты программы. В раскрывшемся перечне выбираем “Символ”.
- На экране отобразится окно, через которое мы можем добавить в документ всевозможные знаки, в том числе, не вынесенные на клавиатуру. Для удобства поиска раскрываем список доступных вариантов для параметра “Набор” и останавливаемся на “Основной латинице”. Щелкаем по знаку “<“, затем – по кнопке “Вставить”. Аналогичным образом вставляем “>”. По готовности закрываем окно.
Примечание: данный метод подходит в исключительных случаях, когда необходимо внести единичные правки в документ, т. к. для полноценной работы с информацией нужна рабочая клавиатура (хотя бы виртуальная).
к. для полноценной работы с информацией нужна рабочая клавиатура (хотя бы виртуальная).
Символ “≠”
Этот символ в виде перечеркнутого знака “равно” предназначен только красивого визуального оформления информации. Он не воспринимается программой как математический, следовательно, в формулах применяться не может.
Т.к. знак не представлен на клавиатуре, его можно найти и вставить только через специальное окно, которое мы рассмотрели выше.
Для параметра “Набор” выбираем вариант – “Математические операторы”
Заключение
Таким образом, в том, чтобы поставить знак “не равно” в Эксель, нет ничего сложного. Для начала нужно определиться с его значением – математическое или визуальное. В первом случае используется комбинация знаков “меньше” и “больше”, во втором – символ в виде перечеркнутого знака “равно”.
Знаки больше, меньше или ровно в математике
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.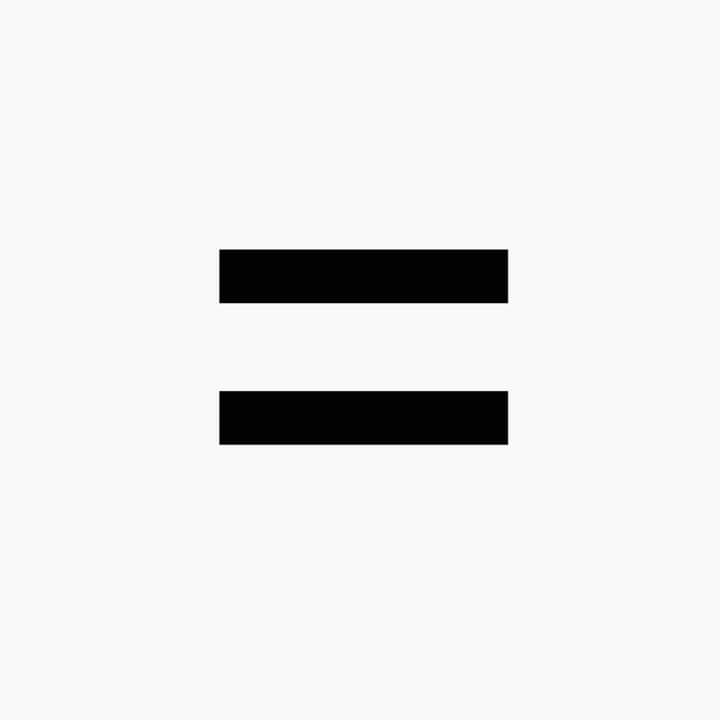
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
- Строгие неравенства — используют только знак больше (>) или меньше (<).
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- неравенства a > b и b < a означают одно и тоже, то есть равносильны.

- Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы неравенств.
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Развивать математическое мышление детей помогут уроки математики в школе Skysmart. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой и влюбиться в числа.
Запишите вашего ребенка на бесплатное пробное занятие в Skysmart: поиграем в цифры вместе с енотом Максом и покажем, что математика — это очень увлекательно!
Символ примерно равно на клавиатуре
Существуют дополнительные команды для ввода символов, недоступных при использовании обычной клавиатуры. Эти команды называются и обозначаются как «Alt+NUM», где «NUM» — число символа, набираемое на цифровой клавиатуре.
Эти команды называются и обозначаются как «Alt+NUM», где «NUM» — число символа, набираемое на цифровой клавиатуре.
Для написания нужного символа в Windows, следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести необходимое число на цифровой клавиатуре. После набора цифр, отпустите клавишу Alt — появится символ.
Например, для вставки длинного тире, нажмите клавишу Alt , наберите на клавиатуре цифры 0 1 5 1 и отпустите Alt — получится длинное тире.
Наиболее частые
↑ Alt + 24: стрелка вверх
↓ Alt + 25: стрелка вниз
→ Alt + 26: стрелка вправо
← Alt + 27: стрелка влево
ø Alt + 0216 (в строчном регистре диаметр, перечеркнутая о)
Alt + 0160: неразрывный пробел
Alt + 255: неразрывный пробел
– Alt + 0150: короткое тире
— Alt + 0151: длинное тире
… Alt + 0133: многоточие
« Alt + 0171: левые кавычки «ёлочки»
» Alt + 0187: правые кавычки «ёлочки»
у́же Alt + 0769: знак ударения
§ Alt + 0167: параграф
Alt + 126: тильда
Alt + 92: обратная косая черта
° Alt + 0176: градус (угол или температура)
± Alt + 0177: плюс/минус
≤ Alt + 8804: меньше/равно
≥ Alt + 8805: больше/равно
≈ Alt + 8776: примерно равно
≠ Alt + 8800: не равно
² Alt + 0178: вторая степень
³ Alt + 0179: третья степень
× Alt + 0215: знак умножения
÷ Alt + 0247: знак деления (обелюс)
£ Alt + 0163: фунт стерлингов
€ Alt + 0128: евро
¥ Alt + 0165: японская иена
© Alt + 0169: копирайт
® Alt + 0174: зарегистрированная торговая марка
™ Alt + 0162: торговая марка
При отсутствии блока цифровой клавиатуры, например на нетбуках, необходимо её включить сочетанием клавиш Fn и F11 или, при наборе дополнительно удерживать клавишу Fn .
Для набора цифр Alt-кода на нетбуках используются функциональные клавиши.
На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа word или excel.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt ;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.
Оба варианта работают в Word, Excel и других офисных программах.
Вставка символа без клавиатуры
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
В первых рядах будет нужный знак.
Похожие знаки равенства
Кроме знака примерного равенства есть много похожих математических и геометрических операндов. Они часто используются в формулах и имеют разную смысловую нагрузку.
| название | юникод | ASCII-код | |
|---|---|---|---|
| ≃ | гомеоморфизм | 2286 | 8788 |
К ним также применимы способы вставки в word и exсel.
От Masterweb
Знак «Примерно равно» в основном используется при печати разнообразных формул и задач. Написание специальных символов от руки не доставляет никаких хлопот. Если же пользователю необходимо вставить знак в электронный документ, возникают проблемы. Особенно если речь идет о символах, используемых в точных науках. Ниже будут рассмотрены все способы записи знака примерного равенства. Какие рекомендации помогут воплотить задумку в жизнь?
Готовые символы
Знак «Примерно равно» на клавиатуре найти не получится. Дело все в том, что этот символ является специальным. Клавиатурную панель можно использовать для печати примерного равенства, но далеко не всегда.
Дело все в том, что этот символ является специальным. Клавиатурную панель можно использовать для печати примерного равенства, но далеко не всегда.
Иногда упомянутый элемент текстового документа проще скопировать и ставить в нужное место. Действовать предлагается таким образом:
- Отыскать текст, где есть знак волнистого равно. Это и есть приблизительное равенство.
- Выделить его любым известным способом.
- Нажать Ctrl + C либо ПКМ + «Копировать».
- Поставить курсор в место предполагаемой печати.
- Зажать Ctrl + V либо ПКМ + «Вставить».
Проделанные действия помогут быстро напечатать скопированный в буфер обмена специальный знак. Этот подход используется не слишком часто, но помнить о нем крайне важно.
Стандартные средства «Виндовс»
Как поставить знак «Примерно равно»? Этот символ предлагается печатать в тексте по-разному. Второй вариант – это использование службы «Виндовс» под названием «Таблица символов». Данная утилита помогает вставлять, копировать и изучать все возможные специальные знаки. И математические символы в том числе.
И математические символы в том числе.
Руководство по воплощению задумки в жизнь будет иметь такую интерпретацию:
- Зайти в службу «Таблица символов». Ее можно отыскать через «Пуск» в папке «Стандартные» – «Служебные».
- Внимательно изучить появившееся окно. Кликнуть по иконке с волнистым равно.
- Нажать на элемент управления под названием «Выбрать». В качестве альтернативы можно дважды кликнуть по изображению символики левой кнопкой мыши.
- Выбрать команду «Копировать» в нижней части окна.
- Вставить в текст скопированный знак «Примерно равно» из буфера обмена в текстовый документ любым удобным способом.
Дело сделано. Как показывает практика, этот вариант развития событий встречается не слишком часто, но он имеет место. Что еще можно предложить пользователям?
Функционал Office
Знак «Примерно равно» иногда вставляют через средства «Офисных» приложений. В нашем случае речь идет о «Ворде». Здесь есть аналог «Таблицы символов» Windows. Эта служба помогает печатать разнообразные символы, особенно те, которых нет на клавиатурной панели.
Эта служба помогает печатать разнообразные символы, особенно те, которых нет на клавиатурной панели.
Что для этого потребуется? Юзеру необходимо выполнить такие действия:
- Перейти к работе инструмента «Вставка». Соответствующий пункт меню находится на панели инструментов Word.
- Щелкнуть по строчке с надписью «Символ». На экране появится небольшое диалоговое окно.
- Отыскать в соответствующем меню миниатюру со знаком приблизительного равенства.
- Осуществить вставку символики двойным кликом по той или иной иконке.
На данном этапе можно закончить все манипуляции. Остается всего лишь закрыть диалоговое окно «Символы» и продолжить набор текста.
Важно: упомянутый знак можно отыскать в шрифте Times New Roman.
Alt-коды в помощь
Как поставить знак «Примерно равно» на клавиатуре? Как уже было сказано, пользователь не сможет ни при каких обстоятельствах отыскать соответствующий элемент на клавиатурной панели. Зато при желании можно без труда напечатать его посредством специализированных команд и кодов. Начнем с самого простого. Речь идет об Alt-кодах. Их иногда называют ASCII-кодами. С помощью специальных комбинаций продвинутые ПК-пользователи печатают различные уникальные символы. И знаки приблизительного равенства не являются исключением.
Начнем с самого простого. Речь идет об Alt-кодах. Их иногда называют ASCII-кодами. С помощью специальных комбинаций продвинутые ПК-пользователи печатают различные уникальные символы. И знаки приблизительного равенства не являются исключением.
Чтобы осуществить их вставку в текст, потребуется:
- Установить курсор-указатель мыши в предполагаемом месте появления знака.
- Активировать режим «Нам Лок» на компьютере. Для этого обычно достаточно нажатия на клавишу Num Lock.
- Нажать на клавишу Alt.
- Напечатать код 8776 при помощи циферной клавиатуры. Она располагается в правой части клавиатурной панели.
- Отпустить нажатые ранее клавиши.
Дело сделано. Символ «Примерно равно» будет установлен в указанном заранее месте. Подобный расклад на практике встречается все чаще. Он значительно упрощает жизнь продвинутым юзерам.
Важно: на клавиатуре можно увидеть разные кнопки «Альт». При работе с ASCII-кодами необходимо воспользоваться одной из соответствующий клавиш. Не важно, с какой стороны клавиатуры.
Не важно, с какой стороны клавиатуры.
Unicode и обработка данных
Последний прием, помогающий быстро поставить к тексте символ примерного равенства – это работа с «Юникодом». Что придется сделать для реализации поставленной задачи? Необходимо придерживаться следующего алгоритма действий:
- Поставить курсор в месте, где должно появиться примерное равенство.
- Набрать на клавиатуре код 2248.
- Одновременно нажать на клавиатуре сочетание «Альт» + Ч (русскую).
Следование руководству приведет к обработке запроса. В ходе него циферный код будет преобразован в тот или иной символ.
Операторы DAX — DAX | Microsoft Docs
- Чтение занимает 6 мин
В этой статье
В языке выражений анализа данных (DAX) операторы используются для создания выражений, которые сравнивают значения, выполняют арифметические вычисления или работают со строками.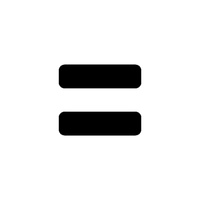 The Data Analysis Expression (DAX) language uses operators to create expressions that compare values, perform arithmetic calculations, or work with strings.
The Data Analysis Expression (DAX) language uses operators to create expressions that compare values, perform arithmetic calculations, or work with strings.
Типы операторовTypes of operators
Существует четыре различных типа вычислительных операторов: арифметические, сравнения, объединения текста и логические.There are four different types of calculation operators: arithmetic, comparison, text concatenation, and logical.
Арифметические операторыArithmetic operators
Для выполнения основных математических операций, таких как сложение, вычитание или умножение, объединения чисел и получения числовых результатов применяются перечисленные ниже арифметические операторы.To perform basic mathematical operations such as addition, subtraction, or multiplication; combine numbers; and produce numeric results, use the following arithmetic operators.
| Арифметический операторArithmetic operator | ЗначениеMeaning | ПримерExample |
|---|---|---|
| + (знак плюса)+ (plus sign) | СложениеAddition | 3+33+3 |
| – (знак минуса)– (minus sign) | Вычитание или знак числаSubtraction or sign | 3–1–13–1–1 |
| * (звездочка)* (asterisk) | УмножениеMultiplication | 3*33*3 |
| ДелениеDivision | 3/33/3 | |
| ^ (крышка)^ (caret) | Возведение в степеньExponentiation | 16^416^4 |
Примечание
Знак плюса может функционировать и как бинарный, и как унарный оператор. The plus sign can function both as a binary operator and as a unary operator. Бинарный оператор требует числа с обеих сторон и выполняет их сложение.A binary operator requires numbers on both sides of the operator and performs addition. При использовании значений в формуле DAX с обеих сторон бинарного оператора DAX пытается привести их к числовым типам данных, если они нечисловые.When you use values in a DAX formula on both sides of the binary operator, DAX tries to cast the values to numeric data types if they are not already numbers. Напротив, унарный оператор можно применять к аргументу любого типа.In contrast, the unary operator can be applied to any type of argument. Символ «плюс» не влияет на тип или значение и просто игнорируется, в то время как оператор «минус», примененный к числовому значению, делает его отрицательным.The plus symbol does not affect the type or value and is simply ignored, whereas the minus operator creates a negative value, if applied to a numeric value.
The plus sign can function both as a binary operator and as a unary operator. Бинарный оператор требует числа с обеих сторон и выполняет их сложение.A binary operator requires numbers on both sides of the operator and performs addition. При использовании значений в формуле DAX с обеих сторон бинарного оператора DAX пытается привести их к числовым типам данных, если они нечисловые.When you use values in a DAX formula on both sides of the binary operator, DAX tries to cast the values to numeric data types if they are not already numbers. Напротив, унарный оператор можно применять к аргументу любого типа.In contrast, the unary operator can be applied to any type of argument. Символ «плюс» не влияет на тип или значение и просто игнорируется, в то время как оператор «минус», примененный к числовому значению, делает его отрицательным.The plus symbol does not affect the type or value and is simply ignored, whereas the minus operator creates a negative value, if applied to a numeric value.
Операторы сравненияComparison operators
Сравнить два значения можно с помощью приведенных ниже операторов.You can compare two values with the following operators. Результатом является логическое значение (TRUE или FALSE).When two values are compared by using these operators, the result is a logical value, either TRUE or FALSE.
| Оператор сравненияComparison operator | ЗначениеMeaning | ПримерExample |
|---|---|---|
| = | РавноEqual to | [Регион] = «Россия»[Region] = «USA» |
| == | Строго равноStrict equal to | [Регион] == «Россия»[Region] == «USA» |
| > | Больше чемGreater than | [Дата продажи] > «Янв 2009″[Sales Date] > «Jan 2009» |
| < | Меньше чемLess than | [Дата продажи] < «1 янв 2009″[Sales Date] < «Jan 1 2009» |
| >= | Больше или равноGreater than or equal to | [Объем] >= 20000[Amount] >= 20000 |
| <= | Меньше или равноLess than or equal to | [Объем] <= 100[Amount] <= 100 |
| <> | Не равноNot equal to | [Регион] <> «Россия»[Region] <> «USA» |
Все операторы сравнения, кроме ==, считают значение BLANK равным числу 0, пустой строке «», дате DATE(1899, 12, 30) или значению FALSE.![]() All comparison operators except == treat BLANK as equal to number 0, empty string «», DATE(1899, 12, 30), or FALSE. Поэтому выражение [Столбец] = 0 будет иметь значение true, если значение [Столбец] равно 0 или BLANK.As a result, [Column] = 0 will be true when the value of [Column] is either 0 or BLANK. Для сравнения [Столбец] == 0 имеет значение true, только когда значение [Столбец] равно 0.In contrast, [Column] == 0 is true only when the value of [Column] is 0.
All comparison operators except == treat BLANK as equal to number 0, empty string «», DATE(1899, 12, 30), or FALSE. Поэтому выражение [Столбец] = 0 будет иметь значение true, если значение [Столбец] равно 0 или BLANK.As a result, [Column] = 0 will be true when the value of [Column] is either 0 or BLANK. Для сравнения [Столбец] == 0 имеет значение true, только когда значение [Столбец] равно 0.In contrast, [Column] == 0 is true only when the value of [Column] is 0.
Оператор объединения текстаText concatenation operator
Используйте амперсанд ( & ) для объединения или сцепления двух или нескольких текстовых строк в один фрагмент текста.Use the ampersand (&) to join, or concatenate, two or more text strings to produce a single piece of text.
| Оператор для работы с текстомText operator | ЗначениеMeaning | ПримерExample |
|---|---|---|
| & (амперсанд)& (ampersand) | Соединяет или сцепляет два значения для получения одного непрерывного текстового значения. Connects, or concatenates, two values to produce one continuous text value Connects, or concatenates, two values to produce one continuous text value | [Регион] & «, » & [Город][Region] & «, » & [City] |
Логические операторыLogical operators
Используйте логические операторы (&&) и (||) для объединения выражений с целью получить один результат.Use logical operators (&&) and (||) to combine expressions to produce a single result.
| Оператор для работы с текстомText operator | ЗначениеMeaning | ПримерыExamples |
|---|---|---|
| && (двойной амперсанд)&& (double ampersand) | Объединяет два выражения, каждое из которых имеет логический результат, условием И.Creates an AND condition between two expressions that each have a Boolean result. Если оба выражения возвращают TRUE, комбинация выражений также возвращает значение TRUE. В противном случае комбинация возвращает FALSE.If both expressions return TRUE, the combination of the expressions also returns TRUE; otherwise the combination returns FALSE.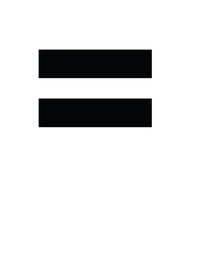 | ([Регион] = «Франция») && ([Покупатель] = «да»))([Region] = «France») && ([BikeBuyer] = «yes»)) |
| || (двойной символ вертикальной черты)|| (double pipe symbol) | Объединяет два выражения условием ИЛИ.Creates an OR condition between two logical expressions. Если любое из выражений возвращает значение TRUE, результатом будет TRUE. Результат будет FALSE, только если оба выражения имеют значение FALSE.If either expression returns TRUE, the result is TRUE; only when both expressions are FALSE is the result FALSE. | (([Регион] = «Франция») || ([Покупатель] = «да»))(([Region] = «France») || ([BikeBuyer] = «yes»)) |
| ININ | Объединяет все строки, сравниваемые с таблицей, логическим условием ИЛИ.Creates a logical OR condition between each row being compared to a table. Обратите внимание, что в синтаксисе конструктора таблицы используются фигурные скобки.Note: the table constructor syntax uses curly braces. | ‘Продукт'[Цвет] IN { «Красный», «Синий», «Черный» }’Product'[Color] IN { «Red», «Blue», «Black» } |
Операторы и порядок приоритетаOperators and precedence order
В некоторых случаях порядок, в котором выполняется вычисление, может влиять на возвращаемое значение. Поэтому важно понимать, как определяется порядок и как можно изменить его, чтобы получить нужные результаты.In some cases, the order in which calculation is performed can affect the Return value; therefore, it is important to understand how the order is determined and how you can change the order to obtain the desired results.
Поэтому важно понимать, как определяется порядок и как можно изменить его, чтобы получить нужные результаты.In some cases, the order in which calculation is performed can affect the Return value; therefore, it is important to understand how the order is determined and how you can change the order to obtain the desired results.
Порядок вычисленияCalculation order
Выражение вычисляет операторы и значения в определенном порядке.An expression evaluates the operators and values in a specific order. Выражения всегда начинаются со знака равенства (=).All expressions always begin with an equal sign (=). Знак равенства указывает на то, что последующие символы образуют выражение.The equal sign indicates that the succeeding characters constitute an expression.
После знака равенства находятся вычисляемые элементы (операнды), разделенные вычислительными операторами.Following the equal sign are the elements to be calculated (the operands), which are separated by calculation operators. Выражения всегда считываются слева направо, но порядок, в котором группируются элементы, можно в некоторой степени контролировать с помощью круглых скобок.Expressions are always read from left to right, but the order in which the elements are grouped can be controlled to some degree by using parentheses.
Выражения всегда считываются слева направо, но порядок, в котором группируются элементы, можно в некоторой степени контролировать с помощью круглых скобок.Expressions are always read from left to right, but the order in which the elements are grouped can be controlled to some degree by using parentheses.
Приоритет операторовOperator precedence
Если в одной формуле имеется несколько операторов, операции производятся в порядке, указанном в таблице ниже.If you combine several operators in a single formula, the operations are ordered according to the following table. Если операторы имеют одинаковый приоритет, они выполняются слева направо.If the operators have equal precedence value, they are ordered from left to right. Например, если выражение содержит оператор умножения и оператор деления, они вычисляются в том порядке, в котором они следуют в выражении слева направо.For example, if an expression contains both a multiplication and division operator, they are evaluated in the order that they appear in the expression, from left to right.
Управление порядком вычисления с помощью круглых скобокUsing parentheses to control calculation order
Чтобы изменить порядок вычисления, следует заключить в круглые скобки часть формулы, которая должна быть вычислена в первую очередь.To change the order of evaluation, you should enclose in parentheses that part of the formula that must be calculated first. Например, приведенная ниже формула возвращает значение 11, так как умножение выполняется до сложения. For example, the following formula produces 11 because multiplication is calculated before addition. Формула умножает 2 на 3, а затем прибавляет 5 к результату.The formula multiplies 2 by 3, and then adds 5 to the result.
For example, the following formula produces 11 because multiplication is calculated before addition. Формула умножает 2 на 3, а затем прибавляет 5 к результату.The formula multiplies 2 by 3, and then adds 5 to the result.
=5+2*3
Если же добавить круглые скобки, порядок изменится: сначала складываются числа 5 и 2, а затем результат умножается на 3, и получается 21.In contrast, if you use parentheses to change the syntax, the order is changed so that 5 and 2 are added together, and the result multiplied by 3 to produce 21.
=(5+2)*3
В приведенном ниже примере из-за круглых скобок вокруг первой части формулы сначала вычисляется выражение (3 + 0.25), а затем результат делится на результат выражения (3 - 0.25).In the following example, the parentheses around the first part of the formula force the calculation to evaluate the expression (3 + 0.25) first and then divide the result by the result of the expression, (3 - 0.
СовместимостьCompatibility
DAX легко обрабатывает и сравнивает различные типы данных, так же как Microsoft Excel.DAX easily handles and compares various data types, much like Microsoft Excel. Однако вычислительная подсистема основана на SQL Server Analysis Services и предоставляет дополнительные возможности реляционного хранилища данных, включая расширенную поддержку типов даты и времени.However, the underlying computation engine is based on SQL Server Analysis Services and provides additional advanced features of a relational data store, including richer support for date and time types. Поэтому в некоторых случаях результаты вычислений или поведение функций могут отличаться от Excel.Therefore, in some cases the results of calculations or the behavior of functions may not be the same as in Excel. Кроме того, DAX поддерживает больше типов данных, чем Excel.Moreover, DAX supports more data types than does Excel. В этом разделе описаны основные различия.This section describes the key differences.
Приведение типов данных операндовCoercing data types of operands
Как правило, операнды слева и справа от любого оператора должны иметь один и тот же тип данных.In general, the two operands on the left and right sides of any operator should be the same data type. Однако если типы данных различаются, DAX в некоторых случаях преобразует их в общий тип данных для применения оператора.However, if the data types are different, DAX will convert them to a common data type to apply the operator in some cases:
- Оба операнда преобразуются в самый большой из возможных общих типов данных.Both operands are converted to the largest possible common data type.
- Затем применяется оператор, если это возможно.The operator is applied, if possible.
Например, предположим, что необходимо перемножить два числа.For example, suppose you have two numbers that you want to combine. Одно из них получено из формулы, например =[Price] * .20, и результат может иметь много знаков после запятой. One number results from a formula, such as =
One number results from a formula, such as =[Price] * .20, and the result may contain many decimal places. Другое является целым числом, предоставленным как строковое значение.The other number is an integer that has been provided as a string value.
В этом случае DAX преобразует оба числа в вещественные, используя самый большой числовой формат, позволяющий хранить оба числа.In this case, DAX will convert both numbers to real numbers in a numeric format, using the largest numeric format that can store both kinds of numbers. Затем DAX выполняет умножение.Then DAX will apply the multiplication.
В зависимости от комбинации типов данных приведение типов может не применяться при операциях сравнения.Depending on the data-type combination, type coercion may not be applied for comparison operations. Полный список типов данных, поддерживаемых DAX, см. в статьях Типы данных, поддерживаемые в табличных моделях и Типы данных в Power BI Desktop.For a complete list of data types supported by DAX, see Data types supported in tabular models and Data types in Power BI Desktop.
При сравнении числовыми считаются типы Integer, Real Number, Currency, Date/time и Blank.Integer, Real Number, Currency, Date/time and Blank are considered numeric for comparison purposes. При выполнении сравнения значение Blank считается равным нулю.Blank evaluates to zero when performing a comparison. Для операций сравнения поддерживаются перечисленные ниже комбинации типов данных.The following data-type combinations are supported for comparison operations.
| Тип данных в левой частиLeft Side Data Type | Тип данных в правой частиRight Side Data Type |
|---|---|
| ЧисловойNumeric | ЧисловойNumeric |
| ЛогическийBoolean | ЛогическийBoolean |
| СтрокаString | СтрокаString |
Другие операции сравнения со смешанными типами данных возвращают ошибку.Other mixed data-type comparisons will return an error. Например, формула =»1″ > 0 возвращает ошибку Операции сравнения DAX не поддерживают сравнение значений типа Text со значениями типа Integer. For example, a formula such as =»1″ > 0 returns an error stating that DAX comparison operations do not support comparing values of type Text with values of type Integer.
For example, a formula such as =»1″ > 0 returns an error stating that DAX comparison operations do not support comparing values of type Text with values of type Integer.
| Типы данных, используемые в DAXData Types used in DAX | Типы данных, используемые в ExcelData Types used in Excel |
|---|---|
| Числа (I8, R8)Numbers (I8, R8) | Числа (R8)Numbers (R8) |
| СтрокаString | СтрокаString |
| ЛогическийBoolean | ЛогическийBoolean |
| DateTimeDateTime | VariantVariant |
| ВалютаCurrency | ВалютаCurrency |
Различия в порядке приоритетаDifferences in precedence order
Порядок приоритета операций в формулах DAX в основном аналогичен тому, который используется в Microsoft Excel, но некоторые операторы Excel, например оператор процента, не поддерживаются.The precedence order of operations in DAX formulas is basically the same as that used by Microsoft Excel, but some Excel operators are not supported, such as percent. Кроме того, не поддерживаются диапазоны.Also, ranges are not supported.
Кроме того, не поддерживаются диапазоны.Also, ranges are not supported.
Поэтому при копировании и вставке формул из Excel внимательно проверяйте их, так как некоторые операторы или элементы могут быть недопустимыми.Therefore, whenever you copy and paste formulas from Excel, be sure to review the formula carefully, as some operators or elements in the formulas may not be valid. Если есть сомнения касательно очередности выполнения операций, рекомендуется использовать круглые скобки, чтобы устранить неоднозначность и получить ожидаемый результат.When there is any doubt about the order in which operations are performed, it’s recommended you use parentheses to control the order of operations and remove any ambiguity about the result.
См. также:See also
Синтаксис DAXDAX syntax
Именование параметров DAXDAX parameter-naming
Перечень специальных символов — Документация Qucs Help 0.0.19
В компоненте “Текст” и в тексте меток осей диаграмм можно использовать специальные символы. Это делается с помощью тэгов LaTeX. В следующей таблице приводится перечень символов, имеющихся в настоящее время.
Это делается с помощью тэгов LaTeX. В следующей таблице приводится перечень символов, имеющихся в настоящее время.
Примечание: Правильное отображение этих символов зависит от шрифта, используемого Qucs!
Строчные греческие буквы
| Тэг LaTeX | Юникод | Описание |
\alpha | 0x03B1 | alpha |
\beta | 0x03B2 | beta |
\gamma | 0x03B3 | gamma |
\delta | 0x03B4 | delta |
\epsilon | 0x03B5 | epsilon |
\zeta | 0x03B6 | zeta |
\eta | 0x03B7 | eta |
\theta | 0x03B8 | theta |
\iota | 0x03B9 | iota |
\kappa | 0x03BA | kappa |
\lambda | 0x03BB | lambda |
\mu | 0x03BC | mu |
\textmu | 0x00B5 | mu |
\nu | 0x03BD | nu |
\xi | 0x03BE | xi |
\pi | 0x03C0 | pi |
\varpi | 0x03D6 | pi |
\rho | 0x03C1 | rho |
\varrho | 0x03F1 | rho |
\sigma | 0x03C3 | sigma |
\tau | 0x03C4 | tau |
\upsilon | 0x03C5 | upsilon |
\phi | 0x03C6 | phi |
\chi | 0x03C7 | chi |
\psi | 0x03C8 | psi |
\omega | 0x03C9 | omega |
Прописные греческие буквы
| Тэг LaTeX | Юникод | Описание |
\Gamma | 0x0393 | Gamma |
\Delta | 0x0394 | Delta |
\Theta | 0x0398 | Theta |
\Lambda | 0x039B | Lambda |
\Xi | 0x039E | Xi |
\Pi | 0x03A0 | Pi |
\Sigma | 0x03A3 | Sigma |
\Upsilon | 0x03A5 | Upsilon |
\Phi | 0x03A6 | Phi |
\Psi | 0x03A8 | Psi |
\Omega | 0x03A9 | Omega |
Математические символы
| Тэг LaTeX | Юникод | Описание |
\cdot | 0x00B7 | знак умножения — точка (центрированная точка) |
\times | 0x00D7 | знак умножения — крестик |
\pm | 0x00B1 | знак плюс минус |
\mp | 0x2213 | знак минус плюс |
\partial | 0x2202 | знак частного дифференцирования |
\nabla | 0x2207 | набла-оператор |
\infty | 0x221E | знак бесконечности |
\int | 0x222B | знак интеграла |
\approx | 0x2248 | символ приближения (волнистый знак равенства) |
\neq | 0x2260 | знак не равно |
\in | 0x220A | символ “содержится в” |
\leq | 0x2264 | знак меньше-равно |
\geq | 0x2265 | знак больше-равно |
\sim | 0x223C | (центрально-европейский) знак пропорциональности |
\propto | 0x221D | (американский) знак пропорциональности |
\diameter | 0x00F8 | знак диаметра (также знак среднего) |
\onehalf | 0x00BD | половина |
\onequarter | 0x00BC | четверть |
\twosuperior | 0x00B2 | квадрат (степень 2) |
\threesuperior | 0x00B3 | степень 3 |
\ohm | 0x03A9 | единица для сопротивления (прописная греческая омега) |
back to the top
Операторы сравнения — JavaScript | MDN
В JavaScript имеются как строгие сравнения, так и сравнения с преобразованием типа операндов. Строгие сравнения (к примеру, ===) истинны только в том случае, если типы сравниваемых значений являются одинаковыми (к примеру: string-string, number-number). Однако, чаще используются сравнения с преобразованием типов (к примеру, ==). Такой тип сравнения, перед тем как непосредственно выполнить сравнение, приводит операнды к одному типу. В случае же абстрактного реляционного сравнения, операнды сперва преобразуются в примитивы, затем приводятся к одному типу, и только после этого сравниваются.
Строгие сравнения (к примеру, ===) истинны только в том случае, если типы сравниваемых значений являются одинаковыми (к примеру: string-string, number-number). Однако, чаще используются сравнения с преобразованием типов (к примеру, ==). Такой тип сравнения, перед тем как непосредственно выполнить сравнение, приводит операнды к одному типу. В случае же абстрактного реляционного сравнения, операнды сперва преобразуются в примитивы, затем приводятся к одному типу, и только после этого сравниваются.
Строки сравниваются на основе стандартного лексикографического упорядочения, используя значения Unicode.
Особенности сравнений:
- Две строки строго равны только в том случае, если они имеют одинаковую длину, и те же символы в одинаковой последовательности и соответствующих позициях.
- Два числа строго равны в том случае, если они численно равны. NaN не равно ничему, в том числе и NaN. Нули с положительным и отрицательным знаком равны.
- Два логических значения (boolean) равны только в том случае, если они оба
истинны (true)илиложны (false).
- Два различных объекта никогда не равны как в строгих, так и в абстрактных сравнениях.
- Сравнение объекта истинно лишь в том случае, если оба операнда ссылаются на один и тот же объект в памяти.
- Виды
nullиundefinedравны себе как в строгом сравнении, так и в абстрактном.
При использовании сравнения с преобразованием типов, следует быть крайне осторожным, так как это может привести к непредвиденным проблемам, связанным с особенностями конвертации различных типов (см. параграф «Использование операторов равенства»).
Равно (==)
Оператор равно сначала приводит операнды к одному типу, и затем применяет строгое сравнение. Если оба операнда являются объектами, то JavaScript сравнивает внутренние ссылки, которые равны в том случае, если они ссылаются на один и тот же объект в памяти.
Синтаксис
x == y
Примеры
1 == 1
"1" == 1
1 == '1'
3 == 5
0 == false
"foo" == "bar"
Не равно (!=)
Оператор не равно возвращает true в том случае, если операнды не равны. Он аналогичен оператору равенства, перед сравнением приводит операнды к одному типу. В случае если оба операнда являются объектами, JavaScript сравнивает внутренние ссылки, которые не равны в том случае, если относятся к разным объектам в памяти.
Он аналогичен оператору равенства, перед сравнением приводит операнды к одному типу. В случае если оба операнда являются объектами, JavaScript сравнивает внутренние ссылки, которые не равны в том случае, если относятся к разным объектам в памяти.
Синтаксис
x != y
Примеры
1 != 2
1 != "1"
1 != '1'
1 != true
0 != false
"foo" != "bar"
Строго равно (===)
Оператор возвращает истину в том случае, если операнды строго равны (см. выше). В отличие от оператора равно, данный оператор не приводит операнды к одному типу.
Синтаксис
x === y
Примеры
3 === 3
3 === '3'
'foo' === 'foo'
Строго не равно (!==)
Оператор строго не равно возвращает истину в том случае, если операнды не равны, или их типы отличаются друг от друга.
Синтаксис
x !== y
Примеры
3 !== '3'
4 !== 3
Больше (>)
Оператор больше возвращает истину в том случае, если значение левого операнда больше, чем правого.
Синтаксис
x > y
Примеры
4 > 3
1 > 5
Больше или равно (>=)
Оператор больше или равно, возвращает истину в том случае, если значение операнда слева больше или равно значению операнда справа.
Синтаксис
x >= y
Примеры
4 >= 3
3 >= 3
Меньше(<)
Оператор меньше, возвращает истину в том случае, если значение операнда слева меньше, чем значение операнда справа.
Синтаксис
x < y
Примеры
3 < 4
5 < 2
Меньше или равно (<=)
Оператор меньше или равно, возвращает истину в том случае, если значение операнда слева меньше, или равно значению операнда справа.
Синтаксис
x <= y
Примеры
3 <= 4
3 <= 3
Стандартные операции равенства с преобразованием типов (== и !=) используют Абстрактный Алгоритм Эквивалентного Сравнения для сравнения двух операндов.![]() Если у операндов различные типы, то JavaScript пытается привести их к одному типу, перед тем как сравнивать их. К примеру, в выражении
Если у операндов различные типы, то JavaScript пытается привести их к одному типу, перед тем как сравнивать их. К примеру, в выражении 5 == '5', строка справа конвертируется в число, и только потом сравнивается.
Операторы строгого равентсва (=== и !==) используют Строгий Алгоритм Эквивалентного Сравнения, и предназначены для сравнения операндов одного типа. Если операнды имеют разные типы, то результат операции сравнения всегда будет ложью. К примеру, выражение 5 !== '5' будет истинным.
Используйте операторы строгого равенства в тех случаях, когда необходимо проверять не только значения операндов, но так же и их типы. Во противном случае, используйте операторы стандартного равенства, которые позволяют сравнить два операнда вне зависимости от их типов.
Когда происходит преобразование типов (т.е в случаях использования нестрогого сравнения), JavaScript преобразует типы String, Number, Boolean и Object, следующим образом:
- При сравнении числа
(Number)и строки(String), JavaScript пытается преобразовать числовой литерал строки в число. Затем полученное число округляется до ближайшего возможного значения типа
Затем полученное число округляется до ближайшего возможного значения типа Number. - Если один из операндов является логическим
(Boolean), то он преобразуется в значение типа(Number). Если значение логического операнда равняется истине(true), то значение этого операнда преобразуется в 1. Иначе — в 0(ложь / false). - Если объект сравнивается с числом или строкой, JavaScript пытается получить значение по умолчанию для данного объекта. Полученное значение преобразуется в примитив, посредством методов
valueOf()иtoString(). Если преобразовать объект не удается, генерируется ошибка времени выполнения. - Обратите внимание на то, что объект преобразуется в примитив, если, и только если, второй операнд является примитивом. В ином случае, операнды сравниваются как объекты, соответственно, операция сравнения вернет истину в том случае, если внутренние ссылки обоих объектов ссылаются на один и тот же объект в памяти.

Внимание: Объекты String имеют тип Object, а не String. Такие объекты используются редко, так что следующий код может вас сильно удивить.
'foo' === 'foo'
var a = new String('foo');
var b = new String('foo');
a == b
a === b
a == 'foo' | Chrome | Firefox (Gecko) | Internet Explorer | Opera | Safari | |
|---|---|---|---|---|---|
| Базовая поддержка | (Да) | (Да) | (Да) | (Да) | (Да) |
| Android | Chrome for Android | Firefox Mobile (Gecko) | IE Mobile | Opera Mobile | Safari Mobile | |
|---|---|---|---|---|---|---|
| Базовая поддержка | (Да) | (Да) | (Да) | (Да) | (Да) | (Да) |
Java. Экспресс-курс: Операторы сравнения
Статья проплачена кошками — всемирно известными производителями котят.
Если статья вам понравилась, то можете поддержать проект.
Операторы сравнения выдают логический результат (boolean). Если условие проверки истинно, оператор выдает true, а если ложно — false. К операторам сравнения относятся < (меньше чем), > (больше чем), <= (меньше чем или равно), >= (больше чем или равно), == (равно), != (не равно). Операторы «Равно» и «не равно» можно использовать для всех примитивных типов данных, однако остальные сравнения нельзя использовать к типу boolean.
| Оператор | Пример использования | Возвращает значение «истинно», если… |
|---|---|---|
| > | a > b | а больше b |
| >= | a >= b | а больше или равно b |
| < | a < b | а меньше b |
| <= | a <= b | а меньше или равно b |
| == | a == b | а равно b |
| != | a != b | а не равно b |
| && | a && b | а и b истинны, b оценивается условно (если а ложно, b не вычисляется) |
| || | a || b | а или b истинно, b оценивается условно (если а истинно, b не вычисляется) |
| ! | !a | а ложно |
| & | a & b | а и b истинны, b оценивается в любом случае |
| | | a | b | а или b истинно, b оценивается в любом случае |
| ^ | a ^ b | а и b различны |
Наиболее часто операции сравнения используют в выражениях, которые управляют оператором if и операторами цикла.
Обратите внимание, что равенство обозначается двумя знаками равно (==), одиночный знак равно (=) — это оператор присваивания. Типичная ошибка начинающих программистов.
Корректный вариант примера:
int x = 5;
int y = 7;
boolean z = a < b; // результат сохраняется в переменной типа boolean
Примеры для оператора if для Java (В C++ используется другой синтаксис!):
int cat_age;
if(cat_age == 4) // нельзя if(cat_age) - нет сравнения
if(cat_age != 9) // нельзя if(!cat_age) - нет сравнения
Помните, что в Java значения true и false не являются числовыми значениями, как в C++, поэтому, чтобы сравнить значение с другим значением, необходимо явно использовать операторы сравнения.
Реклама
Равных символов
| Символ равенства | Имя равно | Десятичное | Hex |
|---|---|---|---|
| = | Знак равенства | & # 61; | & # x003D; |
| ͇ | Объединение знака равенства ниже | & # 839; | & # x0347; |
| ͌ | Объединение почти равно вышеуказанному | & # 844; | & # x034C; |
| ⁼ | Надстрочный знак равно | & # 8316; | & # x207C; |
| ₌ | Подстрочный знак равно | & # 8332; | & # x208C; |
| ≃ | Асимптотически равно | & # 8771; | & # x2243; |
| ≄ | Не асимптотически равно | & # 8772; | & # x2244; |
| ≅ | Приблизительно равно | & # 8773; | & # x2245; |
| ≆ | Приблизительно, но не фактически равно | & # 8774; | & # x2246; |
| ≇ | Ни приблизительно, ни фактически не равно | & # 8775; | & # x2247; |
| ≈ | Почти равно | & # 8776; | & # x2248; |
| ≉ | Почти не равно | & # 8777; | & # x2249; |
| ≊ | Почти равно или равно | & # 8778; | & # x224A; |
| ≌ | Все равно | & # 8780; | & # x224C; |
| ≑ | Геометрически равно | & # 8785; | & # x2251; |
| ≒ | Приблизительно равно изображению | & # 8786; | & # x2252; |
| ≓ | Изображение или приблизительно равно | & # 8787; | & # x2253; |
| ≔ | Двоеточие равно | & # 8788; | & # x2254; |
| ≕ | Равно двоеточие | & # 8789; | & # x2255; |
| ≖ | Кольцо равно | & # 8790; | & # x2256; |
| Equal Symbol | Equal Name | Decimal | Hex |
|---|---|---|---|
| ≗ | Ring Equal To | & # 8791; | & # x2257; |
| ≛ | Звезда равно | & # 8795; | & # x225B; |
| ≜ | Дельта равна | & # 8796; | & # x225C; |
| ≝ | По определению равно | & # 8797; | & # x225D; |
| ≟ | Опрошено Равно | & # 8799; | & # x225F; |
| ≠ | Не равно | & # 8800; | & # x2260; |
| ≼ | предшествует или равно | & # 8828; | & # x227C; |
| ≽ | Успешно или равно | & # 8829; | & # x227D; |
| ⊆ | Подмножество или равно | & # 8838; | & # x2286; |
| ⊇ | Надмножество или равно | & # 8839; | & # x2287; |
| ⊈ | Ни подмножество, ни равное | & # 8840; | & # x2288; |
| ⊉ | Ни надмножество, ни равное | & # 8841; | & # x2289; |
| ⊊ | Подмножество с не равно | & # 8842; | & # x228A; |
| ⊋ | Надмножество с не равно | & # 8843; | & # x228B; |
| ⊑ | Квадратное изображение или равное | & # 8849; | & # x2291; |
| ⊒ | Квадратный оригинал или равный | & # 8850; | & # x2292; |
| ⊜ | в кружке равно | & # 8860; | & # x229C; |
| ⊴ | Нормальная подгруппа или равна | & # 8884; | & # x22B4; |
| ⊵ | Содержит нормальную подгруппу или равную | & # 8885; | & # x22B5; |
| ⋍ | Перевернутая тильда равна | & # 8909; | & # x22CD; |
| Символ равенства | Имя равно | Десятичное | шестнадцатеричное |
|---|---|---|---|
| ⋕ | Равно и параллельно | & # 8917; | & # x22D5; |
| ⋞ | Равно или предшествует | & # 8926; | & # x22DE; |
| ⋟ | Равно или предшествует | & # 8927; | & # x22DF; |
| ⋠ | Не предшествует или не равно | & # 8928; | & # x22E0; |
| ⋡ | Не соответствует или равно | & # 8929; | & # x22E1; |
| ⋢ | Изображение не квадратное или равно | & # 8930; | & # x22E2; |
| ⋣ | Не квадратный оригинал или равный | & # 8931; | & # x22E3; |
| ⋤ | Квадратное изображение или не равное | & # 8932; | & # x22E4; |
| ⋥ | Квадратный оригинал или не равен | & # 8933; | & # x22E5; |
| ⋬ | Необычная подгруппа или равная | & # 8940; | & # x22EC; |
| ⋭ | Не содержит как нормальную подгруппу или равную | & # 8941; | & # x22ED; |
| ⌸ | Apl Функциональный символ Quad Equal | & # 9016; | & # x2338; |
| ⍯ | Apl Функциональный символ Quad Not Equal | & # 9071; | & # x236F; |
| ⥱ | Знак равенства вверху Стрелка вправо | & # 10609; | & # x2971; |
| ⥵ | Стрелка вправо вверху почти равна | & # 10613; | & # x2975; |
| ⧣ | Знак равенства и наклонная параллель | & # 10723; | & # x29E3; |
| ⧤ | Знак равно и наклонен параллельно тильде вверху | & # 10724; | & # x29E4; |
| ⩦ | Знак равенства с точкой ниже | & # 10854; | & # x2A66; |
| ⩮ | Равно Asterisk | & # 10862; | & # x2A6E; |
| ⩯ | Почти как с Circumflex Accent | & # 10863; | & # x2A6F; |
| Equal Symbol | Equal Name | Decimal | Hex |
|---|---|---|---|
| ⩰ | Примерно равно или равно | & # 10864; | & # x2A70; |
| ⩱ | Знак равенства выше Знак плюс | & # 10865; | & # x2A71; |
| ⩲ | Знак плюса вверху знак равенства | & # 10866; | & # x2A72; |
| ⩳ | Знак равенства над оператором тильды | & # 10867; | & # x2A73; |
| ⩴ | Двойное двоеточие Равно | & # 10868; | & # x2A74; |
| ⩵ | Два последовательных знака равенства | & # 10869; | & # x2A75; |
| ⩶ | Три последовательных знака равенства | & # 10870; | & # x2A76; |
| ⩷ | Знак равенства с двумя точками вверху и двумя точками ниже | & # 10871; | & # x2A77; |
| ⪬ | Меньше или равно | & # 10924; | & # x2AAC; |
| ⪭ | Больше или равно | & # 10925; | & # x2AAD; |
| ⪮ | Знак равенства с неровностями вверху | & # 10926; | & # x2AAE; |
| ⪯ | Перед вышеприведенным однострочным знаком равенства | & # 10927; | & # x2AAF; |
| ⪰ | Успешно выше Однострочный знак равенства | & # 10928; | & # x2AB0; |
| ⪱ | Предыдущее однострочное Не равно | & # 10929; | & # x2AB1; |
| ⪲ | Преуспевает Выше Однострочная Не равно | & # 10930; | & # x2AB2; |
| ⪳ | Перед знаком выше Знак равенства | & # 10931; | & # x2AB3; |
| ⪴ | Успешно выше Знак равно | & # 10932; | & # x2AB4; |
| ⪵ | Предыдущее значение не равно | & # 10933; | & # x2AB5; |
| ⪶ | Успех выше не равен | & # 10934; | & # x2AB6; |
| ⪷ | предшествует выше, почти равно | & # 10935; | & # x2AB7; |
| Equal Symbol | Equal Name | Decimal | Hex |
|---|---|---|---|
| ⪸ | Успехов выше Почти равно | & # 10936; | & # x2AB8; |
| ⪹ | Предыдущее значение выше не почти равно | & # 10937; | & # x2AB9; |
| ⪺ | Успех выше не почти равен | & # 10938; | & # x2ABA; |
| ⫃ | Подмножество точек выше или равно им | & # 10947; | & # x2AC3; |
| ⫄ | Надмножество или равное с точкой выше | & # 10948; | & # x2AC4; |
| ⫅ | Подмножество вышеуказанного знака равенства | & # 10949; | & # x2AC5; |
| ⫆ | Надмножество вышеуказанного знака равенства | & # 10950; | & # x2AC6; |
| ⫉ | Указанное выше подмножество почти равно | & # 10953; | & # x2AC9; |
| ⫊ | Надмножество вышеперечисленного почти равно | & # 10954; | & # x2ACA; |
| ⫋ | Вышеуказанное подмножество не равно | & # 10955; | & # x2ACB; |
| ⫌ | Надмножество вышеперечисленного не равно | & # 10956; | & # x2ACC; |
| ⫑ | Замкнутое подмножество или равно | & # 10961; | & # x2AD1; |
| ⫒ | Замкнутое надмножество или равно | & # 10962; | & # x2AD2; |
| ⭀ | Знак равенства вверху Стрелка влево | & # 11072; | & # x2B40; |
| ⭂ | Стрелка влево вверху Назад Почти равно | & # 11074; | & # x2B42; |
| ⭈ | Стрелка вправо вверху Назад Почти равно | & # 11080; | & # x2B48; |
| ⭊ | Стрелка влево вверху Почти равно | & # 11082; | & # x2B4A; |
| ꞊ | Буква-модификатор Краткая Знак равенства | & # 42890; | & # xA78A; |
| ﹦ | Малый знак равенства | & # 65126; | & # xFE66; |
| = | Полная ширина равна сигналу | & # 65309; | & # xFF1D; |
Скопируйте и вставьте символ равенства или используйте десятичное, шестнадцатеричное число или HTML-код в формате Unicode на социальных сайтах, в своем блоге или в документе.
Варианты предварительного просмотра символа равенства
| Символ равенства | Цвет | Курсив |
|---|---|---|
| = | Знак равенства красный | = |
| = | Знак равенства оранжевый | = | Знак равенства розовый | = |
| = | Знак равенства зеленый | = |
| = | Знак равенства королевский синий | = |
| = | Знак равенства фиолетовый | = |
| ͇ | Объединение знака равенства ниже красного | ͇ |
| ͇ | Объединение знака равенства ниже оранжевого | ͇ |
| ͇ | Объединение знака равенства ниже розового | ͇ |
| ͇ | Объединение Знак равенства Ниже зеленого | ͇ |
| ͇ | Объединение равно S ign Под королевским синим | ͇ |
| ͇ | Объединение знака равенства Ниже фиолетового | ͇ |
Странная и праведная история знака равенства
Увеличить / Эта мемориальная доска в честь Роберта Рекорда находится в Музее Тенби в Уэльсе.
Роберт Рекорд был одним из тех людей, которые настолько опередили свое время, что казалось, ему суждено было прийти к трагическому концу. В 16 веке он добился успехов в области экономики, медицины, теологии и поэзии. Но его величайший вклад преподается каждому ученику начальной школы, и он, возможно, заложил основу для современной информатики. Он изобрел знак равенства.
От мочи к научно-популярным
Рекорд родился в 1510 году в Тенби, Уэльс. В 14 лет он поступил в Оксфордский университет.В 21 год он преподавал там математику, хотя стипендия не была его первой целью в карьере. В течение следующих нескольких лет он также получил степень в области медицины и написал монографию с изысканным названием «Писсуар врача », в которой подробно описывалось, что врач может узнать из мочи пациента.
Либо медицина оказалась менее увлекательной, чем ожидал Рекорд, либо менее прибыльной. В течение следующего десятилетия он перешел от медицины к финансам и курировал монетные дворы в Бристоле, Лондоне и Дублине. Однако жизнь писателя явно ему нравилась. Он написал большой и разнообразный труд: богословские трактаты в защиту протестантизма, стихи и, самое главное, учебники.
Однако жизнь писателя явно ему нравилась. Он написал большой и разнообразный труд: богословские трактаты в защиту протестантизма, стихи и, самое главное, учебники.
Рекорд не только объяснял астрономию, геометрию и арифметику в последующих учебниках, но и объяснял их на английском языке. Предыдущие работы по математике были написаны на латыни, а это значит, что единственные, кто мог их читать, уже имели обширное образование. Recorde писал на английском для британского дилетанта.Для этих занятых учеников он придумал свое самое известное изобретение. Его последняя книга, Точильный камень Витте , опубликованная в 1557 году, подарила миру знак равенства.
=
Возможно, человек, обученный изучать мочу и контролировать валюту, обладает прагматическим умом. Recorde счел раздражающим постоянно повторять, что одна сторона уравнения равна другой. Он написал с явным раздражением и причудливым написанием: «И чтобы избежать утомительного повторения этой работы, я поставлю, как я часто делаю это часто в работе, пару параллелей. «Вместо того, чтобы использовать фразу для передачи смысла, он передал бы то же значение с помощью символа. Какой символ может быть более подходящим, чем пара строк одинаковой длины? Ничто, — объяснил Рекорд, -« noe 2 thngs »может быть более чем равным. «
«Вместо того, чтобы использовать фразу для передачи смысла, он передал бы то же значение с помощью символа. Какой символ может быть более подходящим, чем пара строк одинаковой длины? Ничто, — объяснил Рекорд, -« noe 2 thngs »может быть более чем равным. «
Символ Recorde сначала не прижился. Латинский язык все еще господствовал в 16 веке. На латыни было слово для обозначения понятия «aequalis», и если было необходимо больше краткости, люди могли сократить его до «ae» или «oe».«Но популярности знака равенства способствовало введение Рекордом англоговорящих немецких символов« + »и« — ». Комбинация этих знаков позволяла людям быстро и с минимальными затратами чернил выразить математическое уравнение в символах. Вместо того чтобы писать: «Фактор, добавленный к количеству Thryeye, равен dyffyrynte factore frome whyche is takene awaye a Quantitie of foure», математик мог бы написать: «x + 3 = y — 4».
На первый взгляд, это делает Robert Recorde отличной темой для викторин, но не более того. Джон В. Такер, профессор информатики в Университете Суонси и заядлый исследователь теории вычислимости, утверждает, что Рекорд гораздо важнее, чем предполагает его репутация. В книге Robert Recorde: The Life and Times of a Tudor Mathematician Такер описывает, как работа Рекорда заложила фундамент информатики, по крайней мере, среди англоязычных людей:
Джон В. Такер, профессор информатики в Университете Суонси и заядлый исследователь теории вычислимости, утверждает, что Рекорд гораздо важнее, чем предполагает его репутация. В книге Robert Recorde: The Life and Times of a Tudor Mathematician Такер описывает, как работа Рекорда заложила фундамент информатики, по крайней мере, среди англоязычных людей:
Вычислительная техника — это в основном сбор, создание и обработка данных. Он универсален и повсеместен, потому что тесно связан с мирской работой… Чтобы понять историю вычислительной техники, мы можем проследить данные, которые приводят нас к практической математике и к таким писателям, как Рекорд.
Такер считает, что Recorde познакомил Великобританию с концепциями количественной оценки и данных способами, которые были незнакомыми и изменили мир. Его наставления о том, как применять математику в таких областях, как торговля, топографическая съемка, навигация и астрономия, навязали новое мышление людям, которые раньше говорили о количестве в расплывчатых терминах, таких как «хорошая сумма и приличное расстояние». «Recorde помогла ввести точность, точное количественное определение и точное сравнение в повседневную жизнь.
«Recorde помогла ввести точность, точное количественное определение и точное сравнение в повседневную жизнь.
Математика для всех
Recorde также, очевидно, открыл новый способ говорить о числах. Выбирая из латинских и немецких текстов, он познакомил носителей английского языка с такими словами, как «линейный», «деноминационный», «биномиальный» и «уравнение». Он ввел математические значения таких слов, как «квадрат», «составной», «рациональный» и «иррациональный».Роберт Рекорд учил людей говорить на математическом или, что еще более важно, на языке вычислений.
Его самое известное изобретение до сих пор является частью этого вычислительного языка. Знак равенства был впервые использован как часть языка программирования в FORTRAN I в 1957 году. Знак и его вариации, такие как == или ===, по-прежнему используются людьми, которые, как Роберт Рекорд, предпочли бы «Избегайте утомительного повторения этих хлопот, равнозначно». Сегодня компьютерные программисты пожинают плоды работы Рекорда, изобретая точный, поддающийся количественной оценке и эффективный символический язык для описания мира.
К сожалению, Рекорд еще при жизни не считался героем рационального мышления и математического образования. Каким бы блестящим он ни был, он забыл одно из основных правил своего времени: аристократия всегда побеждает. Рекорд был освобожден от должности на монетном дворе Дублина графом Пембруком. Было ли это из-за неудач на некоторых серебряных рудниках, которые Рекорду было поручено разработать, или потому, что он был протестантом, когда на трон взошла набожная католическая королева Мария, остается предметом споров.
Рекорд решил оспорить это с графом, подав на него иск о должностном преступлении.В ответ на это граф подал в суд за клевету. Граф победил. В 1557 году обездоленный Рекорд был брошен в долговую тюрьму, где умер год спустя в возрасте 48 лет.
Что такое знак равенства — объяснение лучше
Легко забыть, что математика — это язык для обмена идеями. Слова «два и три равно пяти» громоздки. Помогает замена чисел и операций символами: «2 + 3 равно 5».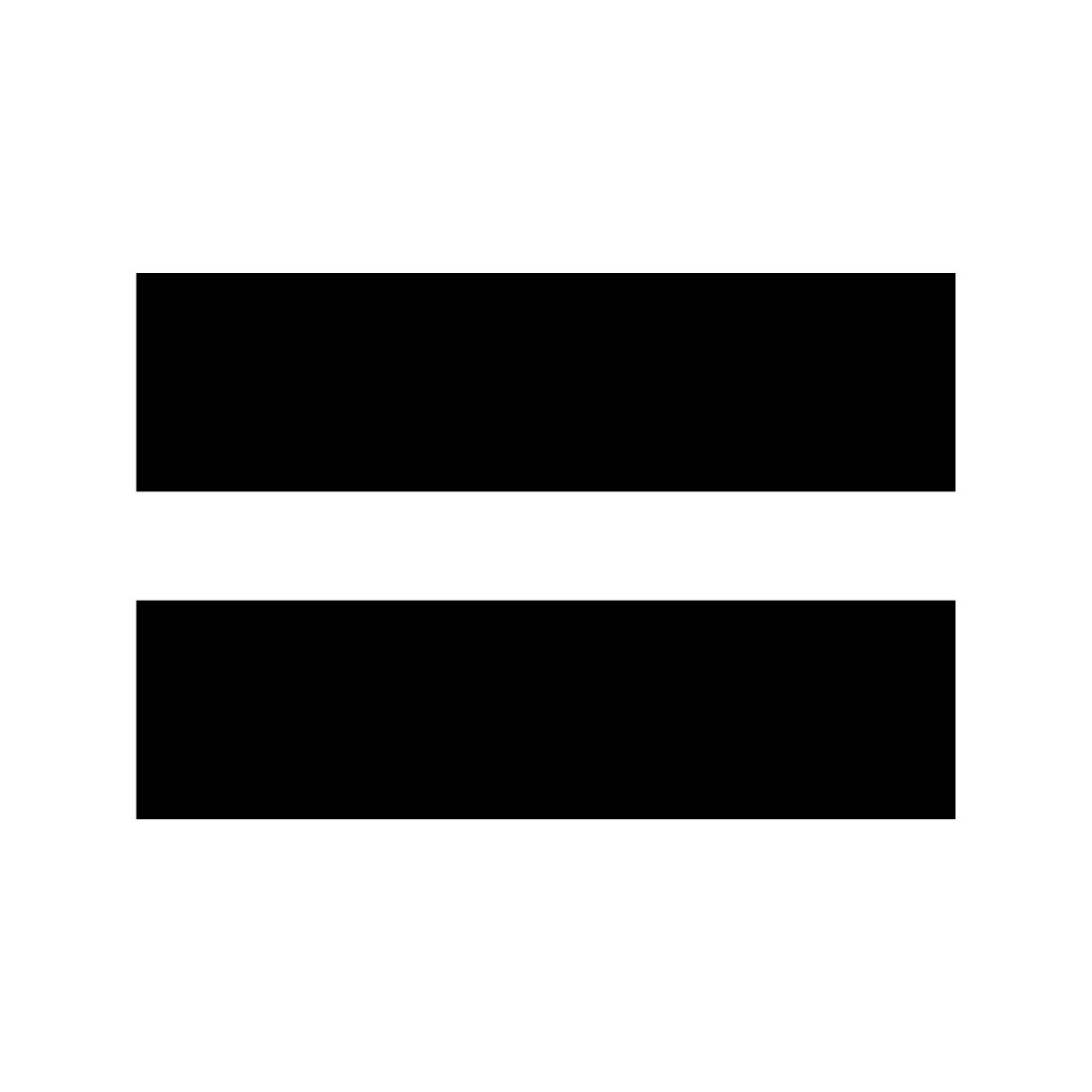
Но мы можем сделать лучше.В 1557 году Роберт Рекорд изобрел знак равенства, написанный двумя параллельными линиями (=), потому что «noe 2 thnges, can be moare equalle».
«2 + 3 = 5» читать намного легче. К сожалению, значение слова «равно» меняется в зависимости от контекста — просто спросите программистов, которым нужно различать =, == и ===.
A «равно» B — это общий вывод: какие конкретные отношения мы пытаемся передать?
Упрощение
Я вижу «2 + 3 = 5» как «2 + 3 можно упростить до 5».2 $ — глубокая математическая истина.
Формула прибавления 1 к n:
, который можно рассматривать как тип геометрической перестановки, комбинаторики, усреднения или даже составления списков.
Фактическое определение
Заявления типа
— это определения по нашему выбору; левая сторона — это ярлык для правой стороны. Это похоже на временное присвоение, но зарезервировано для «фактов», которые не меняются в зависимости от сценария (e всегда имеет одно и то же значение в каждом уравнении, но «скорость» может измениться).
Ограничения
Вот хитрый вопрос. Мы могли бы написать
х + у = 5
х — у = 3
, который указывает условия, которые мы хотим, чтобы было истинным. Я читаю это как «x + y должно быть 5, если возможно» и «x — y должно быть 3, если возможно». Если мы удовлетворяем ограничениям (x = 4, y = 1), отлично!
Если мы не можем достичь обеих целей (x + y = 5; 2x + 2y = 9), тогда уравнения могут быть истинными по отдельности, но не вместе.
Пример: прояснение формулы Эйлера
Распутывание знака равенства помогло мне расшифровать формулу Эйлера:
Действительно, странный зверь.i * pi выбирает живописный маршрут и вращается в воображаемом измерении. Это работает для любой точки на окружности: вращайте в ней или двигайтесь по прямым линиям.
Два пути с одним и тем же пунктом назначения: это , что означает их равенство. Выйдите за рамки общего равенства и найдите более глубокую, конкретную связь («упрощает до», «было выбрано быть», «относится к той же концепции, что и»).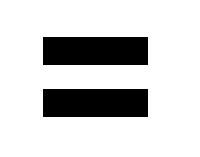
Счастливая математика.
Другие публикации из этой серии
- Развитие математической интуиции
- Почему мы изучаем математику?
- Как развить мышление для математики
- Изучение математики? Думайте как карикатурист.
- Математика как язык: знакомство со знаком равенства
- Как избежать ошибки прилагательного
- В поисках единства в математических войнах
- Краткость прекрасна
- Изучение сложных концепций с помощью метода ADEPT
- Интуиция, детали и метафора лука и стрел
- Учимся учиться: интуиция не обязательна
- Учимся учиться: принимайте аналогии
- Учимся учиться: карандаш, затем чернила
- Учимся учиться: математическая абстракция
- Обучающий совет: исправьте ограничивающий фактор
- Честные и реалистичные руководства по обучению
- Математика, основанная на эмпатии
- Изучение курса (машинное обучение) с помощью метода ADEPT
- Математика и аналогии
- Раскрашенные математические уравнения
- Аналогия: математика и кулинария
- Обучение математике (Mega Man vs.
 Тетрис)
Тетрис)
Некоторые математические символы
Умножение
Есть три широко используемых способа указания умножения
- Символ « x », например, 5 x 6 = 30. Обратите внимание, что этого символа обычно избегают в алгебраических уравнениях из-за обычного использования «x» для обозначения неизвестной величины.
- Символ « * », например 5 * 8 = 40. Использование звездочки для обозначения умножения обычно используется в электронных таблицах (например,g., Excel) и в алгебраических выражениях.
- Или просто число рядом с выражением в скобках, например, 5 (6 + 2) = 40
Отдел
Существует три обычно используемых способа обозначения деления.
- «/», например, 40/5 = 8
- «÷», например, 30 ÷ 5 = 6
- Деление также можно указать, поместив одну величину (числитель) над другой величиной (знаменатель), как показано ниже.
44/123 = 0. 3577
3577
Равно (=) и не равно (≠)
2 + 3 = 5
2 + 3 ≠ 4
(Читается как «не равно» или «не равно».
Меньше (<) и больше (>)
- Символ <означает меньше . Например,
7 <8
200 <300
- Символ> означает больше . Например,
6> 4
3000> 2750
- Символ ≤ означает меньше или равно .
- Символ ≥ означает больше или равно .
Примерно равно
- Символ ≈ означает примерно равный .
Когда вам дается математическое выражение или уравнение, порядок, в котором выполняются математические операции, очень важен. Правила для этого довольно простые. Рассмотрим следующий пример:
2 + (7 + 3) * 3 2 + 4 * (3-1) + 10
Сначала это может показаться устрашающим, но на самом деле это довольно просто.![]() Правила приведены в таблице ниже.
Правила приведены в таблице ниже.
Порядок операций
|
Итак, в приведенном выше примере вы бы:
- Решить в скобках
- Вычислить экспоненты
- Выполните умножение и деление
- Выполнить сложение и вычитание
И правильный ответ — 110.
вернуться наверх | предыдущая страница | следующая страница
Равно, меньше и больше символов
Наряду со знакомым знаком равенства (=) он также очень полезен, чтобы показать, не равно ли что-то (≠) больше чем (>) или меньше (<)
Это важные признаки, которые следует знать :
| = | Когда два значения равны | пример: 2 + 2 = 4 |
| ≠ | Когда два значения определенно не равны | пример: 2 + 2 ≠ 9 |
| < | Когда одно значение меньше другого | пример: 3 <5 |
| > | Когда одно значение больше другого | пример: 9> 6 |
меньше и больше
Знаки «меньше» и «больше» выглядят как буква «V» на своей стороне, не так ли?
Чтобы запомнить, в какую сторону идут знаки «<» и «>», просто запомните:
«Маленький» конец всегда указывает на меньшее число, например:Символ большего, чем: БОЛЬШОЙ> маленький
Пример:
10> 5
«10 это больше 5″
Или наоборот:
5 <10
«5 — меньше 10″
Вы видите, как символ «указывает» на меньшее значение?
. .. Или равно …
.. Или равно …
Иногда мы знаем, что значение меньше, но также может быть равно !
Например, кувшин вмещает до 4 чашек воды.
Итак, сколько в нем воды?
Это может быть 4 чашки или меньше 4 чашек: Итак, пока мы не измерим, все, что мы можем сказать: «меньше или равно » 4 чашки.
Чтобы показать это , мы добавляем дополнительную строку внизу символа «меньше» или «больше чем», например:
Знак «меньше или равно »: | ≤ | |
Знак «больше или равно «: | ≥ |
Все символы
Вот список всех символов:
Символ | слов | Пример использования |
|---|---|---|
= | равно | 1 + 1 = 2 |
≠ | не равно | 1 + 1 ≠ 1 |
> | больше | 5> 2 |
< | менее | 7 <9 |
≥ | больше или равно | мрамора ≥ 1 |
≤ | меньше или равно | собаки ≤ 3 |
Зачем они нужны?
Потому что есть вещи, которые мы точно не знаем. ..
..
… но может еще сказать что-то про .
Итак, у нас есть способы сказать то, что мы знаем (что может быть полезно!)
Пример: у Джона было 10 шариков, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть меньше 10:
Мрамор < 10
Если у Джона все еще есть шарики, мы также можем сказать, что у него больше нуля шариков:
Мрамор > 0
Но если бы мы думали, что Иоанн мог иметь потерять все своих шариков, мы бы сказали
Мрамор ≥ 0
Другими словами, количество шариков больше или равно нулю.
Объединение
Иногда мы можем сказать две (или более) вещи в одной строке:
Пример: Бекки начинает с 10 долларов, что-то покупает и говорит: «У меня тоже есть сдача». Сколько она потратила?
Сколько она потратила?
Ответ: Что-то больше 0 и меньше 10 долларов (но НЕ 0 или 10 долларов):
«На что тратит Бекки»> 0
«На что тратит Бекки» <10 9 1065
Это можно записать одной строкой:
0 долларов <"Сколько тратит Бекки" <10 9 1514
Это говорит о том, что 0 долларов меньше, чем «То, что Бекки тратит» (другими словами, «То, что Бекки тратит» больше, чем 0 долларов), а то, что Бекки тратит, также меньше 10 долларов.
Обратите внимание, что «>» перевернулось на «<", когда мы поставили перед , сколько тратит Бекки. Всегда проверяйте малый конец указывает на малое значение .
Смена сторон
В предыдущем примере мы видели, что когда мы меняем стороны, мы также переворачиваем символ.
| Это: | Бекки тратит> $ 0 | (Бекки тратит более $ 0) | ||
| то же самое: | $ 0 <Бекки тратит | (0 долларов меньше, чем тратит Бекки) |
Просто убедитесь, что маленький конец указывает на маленькое значение!
Вот еще один пример использования «≥» и «≤»:
Пример: у Бекки есть 10 долларов, и она идет за покупками. Сколько она потратит (без использования кредита)?
Сколько она потратит (без использования кредита)?
Ответ: Что-то большее или, возможно, равное 0 долларов США и меньшее или, возможно, равное 10 долларам:
Бекки тратит ≥ 0 долларов
Бекки тратит ≤ 10 долларов 9 1065
Это можно записать одной строкой:
0 долл. США ≤ Бекки тратит ≤ 10 долл. США 9 1514
Длинный пример: перерезание каната
Вот интересный пример, о котором я подумал:
Пример: Сэм разрезает 10-метровую веревку на две части.Какова длина более длинного куска? Какова длина более короткого отрезка?
Ответ: Назовем длинную длину веревки « L », а более короткую длину « S »
.L должен быть больше 0 м (иначе это не кусок веревки), а также меньше 10 м:
L> 0
L <10
Итак:
0
Это говорит о том, что L (более длинная длина веревки) находится между 0 и 10 (но не 0 или 10)
То же самое можно сказать и о более короткой длине « S »:
0
Но я сказал, что есть «короче» и «длиннее», поэтому мы также знаем:
S
(Вы видите, насколько изящна математика? Вместо того, чтобы говорить «меньшая длина меньше, чем большая длина», мы можем просто написать « S
Мы можем объединить все это так:
0
Это говорит о многом:
0 меньше короткой длины, короткой длины меньше длинной, длинной меньше 10.
Если читать «задом наперед», то можно увидеть:
10 больше длинной длины, длинная длина больше короткой длины, короткая длина больше 0.
Это также позволяет нам увидеть, что «S» меньше 10 («перепрыгивая» через «L»), и даже что 0 <10 (что мы все равно знаем), все в одном операторе.
ТЕПЕРЬ у меня есть еще одна хитрость. Если бы Сэм очень старался, он мог бы разрезать веревку ТОЧНО пополам, так что каждая половина составляет 5 м, но мы знаем, что он этого не сделал, потому что мы сказали, что есть «короче» и «длиннее» длина, поэтому мы также знаем:
S <5
и
L> 5
Мы можем вставить это в наше очень аккуратное заявление здесь:
0
И ЕСЛИ мы думали, что две длины МОГУТ быть ровно 5, мы можем изменить это на
. 0 Пример использования алгебры
Хорошо, этот пример может быть сложным, если вы не знаете алгебру, но я подумал, что вы все равно можете его увидеть:
Пример: что такое x + 3, когда мы знаем, что x больше 11?
Если x> 11, , то x + 3> 14
(Представьте, что «x» — это количество людей на вашей вечеринке. Если на вашей вечеринке более 11 человек, а прибывают еще 3, значит, сейчас на вашей вечеринке должно быть более 14 человек.)
Если на вашей вечеринке более 11 человек, а прибывают еще 3, значит, сейчас на вашей вечеринке должно быть более 14 человек.)
Знак равенства — больше хлопот, чем оно того стоит?
Что делать со знаком равенства?
Общая проблема
Начните с 7 шариков, сложите 3, добавьте еще 3, затем вычтите 8. Многие ученики напишут это в качестве ответа:
7 + 3 = 10 + 3 = 13 — 8 = 5 9 1065
Теперь каждая операция выполняется правильно, но на самом деле все это неверно, поскольку первые выражения (7 + 3 и 10 + 3) не равны последнему выражению (13-8) или конечному числу.
Это называется «равным», и это совершенно неверно.
В статье «Понимание студентами знака равенства» мы узнаем, что 70% учащихся средних классов в США имели неправильные представления о знаке равенства (исследование Роберта М. и Мэри Капраро из Техасского университета A&M).
В качестве примера приводят следующий вопрос:
4 + 3 + 2 = () + 2
Многие студенты неправильно складывают все слева, помещают это в скобки, а затем переходят к добавлению последних 2.![]()
4 + 3 + 2 = (9) + 2 = 11
Вопрос действительно требует следующего:
4 + 3 + 2 = (7) + 2 = 9 9 1065
Почему студенты делают такие ошибки?
Фон
Одна из первых вещей, которую мы узнаем в математике, — это знак равенства. Считаем 4 блока, складываем 2 блока и получаем 6 блоков. Кто-то (из лучших побуждений) говорит нам, что мы можем написать это так:
4 + 2 = 6
Знаете ли вы, что знак равенства появился относительно недавно, и что математики прекрасно обходились без него в течение тысяч лет?
Знак равенства «=» был изобретен Робертом Рекордом из Уэльса в середине 16 века.Он использовал параллельные линии одинаковой длины, потому что «ничего не могло быть равнее».
До изобретения символа «=» математики использовали полезные и выразительные слова для обозначения происходящего. Поэтому при добавлении они использовали «дает» или «дает». Другие ранние символы для равных включали «æ» (от латинского « aequalis ») и 2 вертикальные параллельные линии, ||.
За прошедшие годы для знака «=» появилось несколько различных значений, и это может привести к путанице учащихся.
Значение №1 — результат выполнения операции
В примере 4 + 2 = 6 «get 6 блоков» в моем английском предложении записывается как «= 6» при переводе в оператор с использованием только символов.
Значение # 2 — разложение
Что, если мы перевернем приведенное выше утверждение и запишем его следующим образом?
6 = 4 + 2
Теперь знак «=» не представляет ту же концепцию, что и наш знак «=» в предыдущем примере 4 + 2 = 6.
Теперь это означает, что мы начинаем с 6, а разложили на 4 + 2.Но мы также можем разложить 6 любым из следующих способов:
6 = 3 + 3
6 = 2 + 4
6 = 5 + 1
6 = 0 + 6
На этот раз у нас есть бесконечное множество ответов. Очевидно, что «=» здесь используется иначе, чем в примере 4 + 2 = 6, где у нас был один возможный ответ (конечно, при условии, что мы говорим только о реальных числах), в то время как второй набор примеров начинается с одного числа и предлагает очень открытый набор решений.
Значение # 3 — эквивалент 2 операций
Теперь рассмотрим другой случай.
5 + 9 = 7 × 2
Здесь знак «=» снова означает другое. Теперь нам нужно сделать что-то с выражением слева (сложить их), а сделать что-то другое с разными числами справа (умножить их), и после всего этого мы можем сделать вывод, что действительно обе стороны имеют одинаковое значение .
Значение # 4 — эквивалент в наборах
В теории множеств «равно» — это не то же самое, что «эквивалент».
Например, набор {1,2,3} эквивалентен набору {a, b, c}, поскольку они оба имеют одинаковое количество элементов (одинаковое количество элементов), но они не равны , поскольку они не содержат одинаковых элементов.
Также мы можем написать {1, 2, 3} = {2, 1, 3} (они равны ), поскольку элементы в наборе точно такие же, но порядок не имеет значения.
Значение # 5 — эквивалентность в уравнениях
У нас может быть эквивалентных уравнений .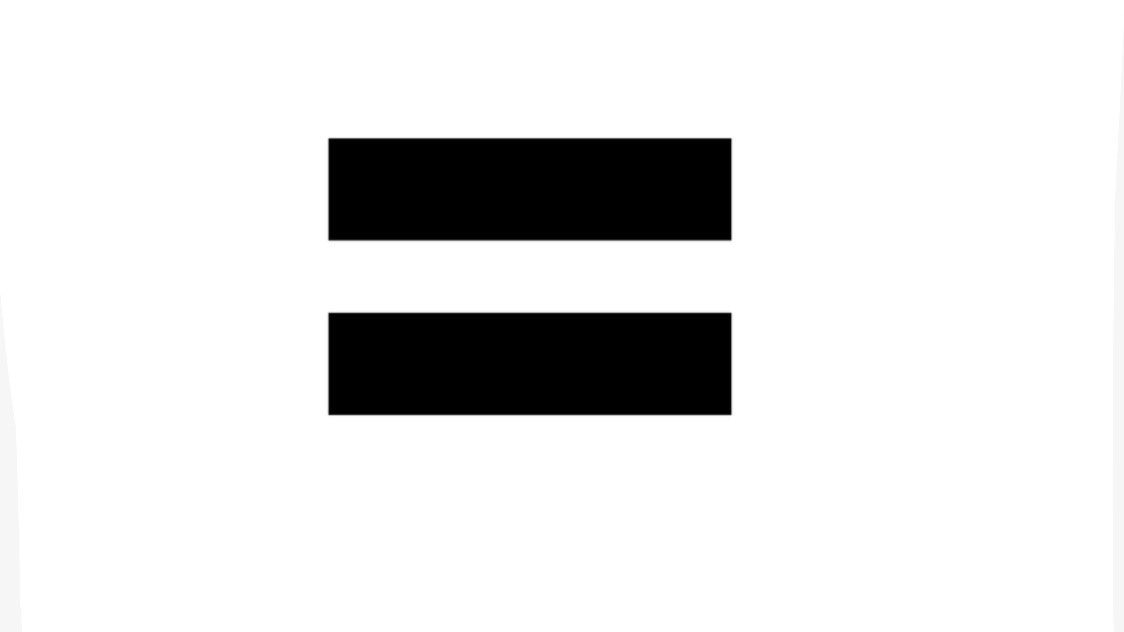 Например, следующие 2 уравнения эквивалентны, поскольку имеют один и тот же набор решений:
Например, следующие 2 уравнения эквивалентны, поскольку имеют один и тот же набор решений:
x + 2 = 7
3 x = 15
Оба уравнения дают нам x = 5.Мы не можем сказать, что у нас есть «равные уравнения», но мы используем термин «эквивалент».
Значение # 6 — эквивалентность в отношениях
Две дроби могут быть эквивалентны :
Они выглядят по-разному, но имеют одинаковую стоимость.
Обратите внимание, что я использовал символ «3 горизонтальных линии» (≡) для «эквивалента». В этом примере мы также можем сказать «равно».
Значение # 7 — как предел
Следующий вызов вызывает много споров. Начните с 0.9. Затем возьмите большее число 0,99. Мы приблизились к 1, верно?
Теперь продолжайте. 0,99999 … Очевидно, если мы зайдем (бесконечно) достаточно далеко, мы получим такой результат:
0,999 … = 1
Здесь используется концепция, совершенно отличная от первых трех значений «=», приведенных выше. Он точно равен 1? Разве нам не нужно какое-то «ограничение»?
Он точно равен 1? Разве нам не нужно какое-то «ограничение»?
Вот еще один. Будучи иррациональным, пи не может точно «равняться» некоторому числу. Или может?
Мы можем показать, что пи имеет следующее значение:
Следует писать «=» или «≈» (примерно равно)?
Значение # 8 — использование в пруфах
Вот еще одно место, где многие студенты отключаются — доказательство тождественности тригонометрии.Скажите, что вопрос:
Доказательство
Многие студенты пытаются найти решение примерно так:
Теперь, по сути, шаги правильные, но сложно следовать логике. Что мы должны делать: слева направо, сверху вниз или их сочетание?
Ученик проделал параллельную работу по левой и правой сторонам, пока не получил что-то, что выглядело бы одинаково с обеих сторон.
Это не лучшее доказательство, поскольку нет четкого определения того, с чего мы начинаем и что делаем на каждом этапе.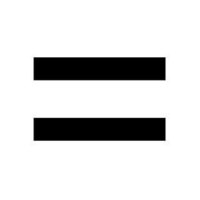
Некоторые возможные решения проблемы со знаком «=»
Компьютерные языки и системы компьютерной алгебры используют разные символы для разных значений знака равенства.
Это может быть хорошим решением для математики.
В компьютерном языке PHP , например (который используют IntMath и squareCircleZ), «=» используется для присвоения значения переменной, а «==» используется для проверки равенства.
Так, например, следующий оператор означает, что с этого момента в программе переменная «а» будет иметь значение 5.
а = 5
Если нам нужно проверить, выполняется ли какое-либо условие, например, имеет ли переменная «b» значение 3, мы должны написать:
if (b == 3) {
[сделать что-нибудь …]
}
В системе компьютерной алгебры Mathematica знак «==» используется для решения уравнений, как показано ниже:
Вход: Решить [2x == 6, x] Выход: {x-> 3}
Обратите внимание на символ «->» для равенства на выходе.
Для сравнения конкурирующая программа Mathcad имеет 4 разных знака равенства:
Присвоение (: =) Чтобы присвоить значение переменной, необходимо использовать нотацию «двоеточие равно», которая выглядит следующим образом:
а: = 5
Показать значение (=) Чтобы отобразить значение переменной «b» в Mathcad, вы просто набираете «b =», и появится значение:
б = 8
Символьное равенство (=) Для вычисления символьного выражения используется символ «жирным шрифтом равно»:
b + b = 2b
Глобальное присвоение (≡) Это математический символ «идентично равен».Это используется, когда вы хотите исправить переменную на всем математическом листе, не допуская ее изменения другими переменными:
c ≡ 8
Однако это значение отличается от того, которое используется в математике. Но поскольку символ идентичности предполагает «сильных равных», возможно, это уместно.
Отчасти проблема?
Это снимок экрана из видеоролика, в котором рассказывается о достоинствах интерактивных досок для обучения математике.
Вопрос инструктора: «Оцените уравнение».Вы действительно можете «вычислить уравнение»?
Вы можете решить уравнение для некоторой переменной или указать, что выражения равны в уравнении, но вы не можете вычислить уравнение.
Источник: eSchoolNews
Нам нужно быть осторожными при формулировании математических вопросов, поскольку именно здесь могут возникнуть неправильные представления.
Сводка
Так почему ученики делают ошибки со знаком равенства? Скорее всего, потому, что в значении знака равенства есть несколько нюансов.
Возможно, нам нужно рассмотреть возможность использования более широкого набора символов для различных типов равных. Одно из мест, где можно посмотреть, — это обозначения, используемые в компьютерных языках или в системах компьютерной алгебры.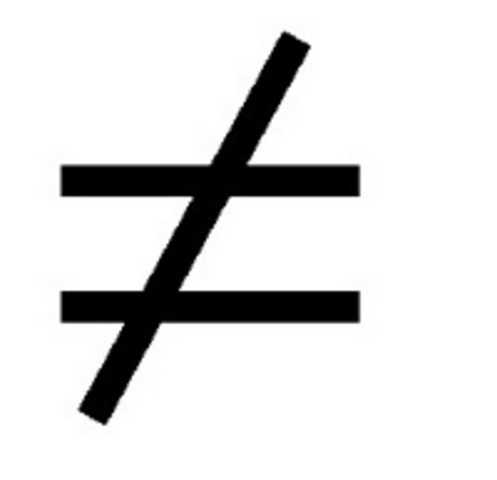
См. 28 комментариев ниже.
Знак «не равно»: что означает ≠ и как его набрать?
Знак « не равно » или «не равно» является выражением неравенства между двумя разными числами, переменными, целыми числами или понятиями. Это вариация знака равенства, который является выражением математического равенства.Знак «не равно» можно ввести с помощью следующих команд: U + 2260; 2260, Alt + X в Microsoft Windows. Вы также можете определить значение Unicode ≠ , а затем использовать средство ввода Unicode для создания собственных сочетаний клавиш.
Давайте посмотрим, как знак «не равно» используется в математике и в других контекстах, а также как он соотносится с обычным знаком равенства.
«Математика — это не числа, уравнения, вычисления или алгоритмы; это о понимании ». — Уильям Пол Терстон
Что такое Unicode / ASCII?
Фото: Автор неизвестен — de: Bild: Unicode logo.jpg, Public Domain, https://commons. wikimedia.org/w/index.php?curid=12627185
wikimedia.org/w/index.php?curid=12627185Специальные символы, такие как «не равно» или символ неравенства, вводятся вместе с определенными символами Unicode. Юникод — это система стандартизации для кодирования и отображения текстовых символов и символов. Консорциум Unicode содержит более 137 000 символов, охватывающих разные языки, сценарии, символы и даже смайлы. Символы Unicode широко используются в компьютерном программном обеспечении и языках программирования благодаря обеспечению единообразного стандарта для операционных систем и языков.UTF-8 — это основной тип кодировки, используемый во всемирной паутине, и он позволяет отображать символ «≠».
Диаграмма ASCII от propr до 1972 года. Фото: неизвестное должностное лицо или служащий правительства США — http://archive.computerhistory.org/resources/text/GE/GE.TermiNet300.1971.102646207.pdf (документ отсутствует в ссылка дана), Public Domain, https://commons.wikimedia.org/w/index.php?curid=63485656 Американский стандартный код для обмена информацией, или ASCII, является более старым стандартом кодирования, на смену которому пришел Unicode, хотя он все еще используется во многих местах.![]() Специальные символы Unicode и ASCII, символы, отсутствующие на клавиатуре, можно вводить с помощью ряда команд, таких как нажатие клавиши ALT и ввод соответствующего числа для символов ASCII. Для поиска специальных символов существуют диаграммы и базы данных символов.
Специальные символы Unicode и ASCII, символы, отсутствующие на клавиатуре, можно вводить с помощью ряда команд, таких как нажатие клавиши ALT и ввод соответствующего числа для символов ASCII. Для поиска специальных символов существуют диаграммы и базы данных символов.
История знака равенства
Знак равенства / равенства — это математический символ, используемый для подтверждения равенства между двумя выражениями. На большинстве клавиатур есть ярлык для ввода знака равенства, расположенный над скобками на раскладке QWERTY.
Изображение Роберта Рекорда. Фото: Автор: Первоначально загрузил Lumos3 из английской Википедии. — Перенесено из en.wikipedia в Commons., Public Domain, https://commons.wikimedia.org/w/index.php?curid=3098302 Считается, что слово «равный» произошло от латинского термина «æqualis», который можно примерно перевести как «даже», «идентичный» или «однородный». Считается, что знак равенства был изобретен около 1557 года Робертом Рекордом. Рекорд был валлийским математиком, который первым использовал гораздо больший и широкий знак равенства для представления двух эквивалентных элементов, назвав их параллельными линиями или «линиями Гемоу» (двойные линии).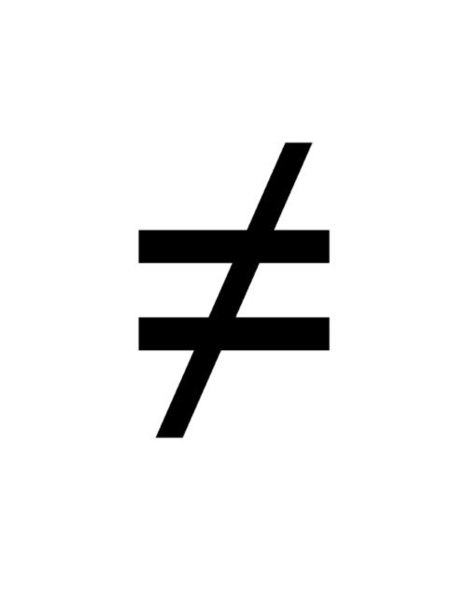 Сообщается, что Recorde обнаружил, что необходимость многократно заявлять, что два значения равны друг другу, отнимает много времени и раздражает, разработав сокращение, чтобы передать значение эквивалентности.
Сообщается, что Recorde обнаружил, что необходимость многократно заявлять, что два значения равны друг другу, отнимает много времени и раздражает, разработав сокращение, чтобы передать значение эквивалентности.
Хотя новый знак равенства Recorde лаконично подразумевает равенство между двумя значениями, он не получил широкого распространения до намного позже.Одна из причин, по которой символ Рекорда, возможно, не сразу прижился, заключалась в том, что в XVI веке латынь все еще сильно влияла на общение, и термин «aequalis» часто просто сокращался до «Ae» или «oe», если требовалось сокращение. Тем не менее, Recorde познакомила англоговорящих с теперь известными немецкими символами вычитания и сложения: «+» и «-». Это дало знаку равенства Recorde дополнительное влияние, так как в сочетании с + и — знак равенства можно было легко использовать для утверждения математических уравнений, выписывать которые требовалось гораздо больше времени. Вертикальный знак равенства, а не горизонтальный знак равенства, возможно, использовался на протяжении 1600-х годов, а теперь повсеместно используемый горизонтальный знак равенства стал стандартизирован в течение 1700-х годов.
Вертикальный знак равенства, а не горизонтальный знак равенства, возможно, использовался на протяжении 1600-х годов, а теперь повсеместно используемый горизонтальный знак равенства стал стандартизирован в течение 1700-х годов.
«Математика — это язык Вселенной. Так что чем больше уравнений вы знаете, тем больше вы можете общаться с космосом ». — Нил ДеГрасс Тайсон
Можно утверждать, что Recorde заложил основу дисциплины информатики, поскольку информатика лежит в основе обработки, создания и сбора данных.Знак равенства Recorde и другой вклад в математическую теорию и операторов дали компьютерным специалистам повсеместно распространенный и общепризнанный символ для присвоения значений и подтверждения качества. Помимо этого, Реркорд помог познакомить мир в целом с концепциями обработки данных и количественной оценки, с теориями и инструкциями по применению математики в различных областях, таких как навигация, коммерция, топографическая съемка и астрономия.
Использование знака равенства
В математике использование знака равенства означает, что два оператора или переменные эквивалентны друг другу.Однако знак равенства часто используется в других областях, например, в компьютерном программировании. Фортран считается первым компьютерным языком, в котором используется знак равенства, этот знак был включен в версии FORTRAN в 1957 году. В языках компьютерного программирования в целом знак равенства не означает, что две вещи эквивалентны. , он функционирует как оператор присваивания, устанавливая значение некоторого оператора в следующий оператор.
Фото: Джон Сотер через Wikimedia Commons, общественное достояние На других компьютерных языках может использоваться знак равенства с традиционным значением «эквивалентности».Примеры обоих типов использования знака равенства можно найти в современных языках программирования. Такие языки, как Perl, Python и C, продолжают использовать знак равенства в качестве оператора присваивания, в то время как такие языки, как Eiffel, Asa и APL, используют знак равенства для обозначения эквивалентности.
Языки программирования, в которых символ равенства не используется в качестве утверждения равенства, имеют другие методы обработки этого сравнения на равенство. Например, Python использует двойной знак равенства («==») в качестве оператора сравнения, поскольку одинарный знак равенства используется как оператор присваивания.Точно так же PHP использует три знака равенства, чтобы делать утверждения о равенстве значений, показывая, что выражения имеют равные значения и используют один и тот же тип данных. Между тем, Javascript использует тройной знак равенства для обозначения «равенства без приведения типов».
«Математика обладает не только истиной, но и высшей красотой — красотой холодной и суровой, как у скульптуры». — Бертран Рассел
Другие случаи использования знака равенства включают использование знака в химии, где он сигнализирует о наличии двойной связи между атомами.В области лингвистики иногда используется знак равенства для обозначения границ клитики, при этом знак ставится между словом, к которому прикреплена клитика, и самой клитикой.
Обратите внимание, что знак может иногда использоваться для соединения этапов математических операций нестандартным способом. Иногда люди будут записывать такие операции:
2 + 3 = 5 + 6 = 11 + 4 = 15
Цель состоит в том, чтобы представить сложение первых двух чисел вместе с последующим сложением еще одного числа.Однако это неправильное обозначение. Чтобы представить это правильно, нужно представить различные вычисления с запятыми между ними:
2 + 3 = 5, 5 + 6 = 11, 11 + 5 = 15
Не равно и другие варианты со знаком равенства
Не равно знак (≠) можно записать с помощью определенных команд Unicode, например U + 2260; 2260, Alt + X в Microsoft Windows. Однако из-за сложности использования таких команд для обозначения неравенства часто используется ряд альтернатив. Восклицательный знак в сочетании со знаком равенства или косая черта в сочетании со знаком равенства часто используются вместо знака «не равно» («! =» И «/ =»).Эти заменители символа неравенства часто используются в языках программирования, поскольку они ограничены символами ASCII и основными символами на клавиатуре, и по этой причине они обычно используют «~ =», «/ =», «! = »Или« <> »в знак неравенства.
Хотя есть некоторые разногласия относительно точного происхождения символов «! =» Для знака «не равно», одна из гипотез происхождения символа заключается в том, что он происходит из языка компьютерного программирования C, который использовался в более ранних языках, таких как FORTRAN. «.ne », чтобы утверждать, что две ценности не равны друг другу.
Помимо знака «не равно», существуют другие варианты знака равенства. Знак «≈» используется для обозначения приблизительной эквивалентности двух терминов, чтобы показать, что два термина почти, но не в точности эквивалентны друг другу. Этот символ примерно равного имеет свои варианты, которые включают один символ «~» для обозначения пропорциональности. Символ «~» также иногда используется для обозначения приблизительно равного символа из-за сложности, с которой многие люди сталкиваются с набором символов Unicode.
«Не беспокойтесь о ваших трудностях с математикой. Уверяю вас, мои еще лучше. — Альберт Эйнштейн
Тройная черта вместо двойной черты, как у знака равенства, иногда используется для обозначения определений математических терминов, обозначения тождеств для значений / переменных и отношений конгруэнтности в алгебраических операциях. Изоморфизм «≅» часто используется для обозначения конгруэнтности геометрических фигур или для обозначения изоморфных алгебраических структур.»Означает возведение в степень
Изоморфизм «≅» часто используется для обозначения конгруэнтности геометрических фигур или для обозначения изоморфных алгебраических структур.»Означает возведение в степень
В линейной алгебре или информатике эти математические операторы могут иметь разные определения. При работе с матричными и строковыми массивами следующие операторы имеют следующие определения:
- «!» представляет собой вертикальную конкатенацию матриц
- «~» представляет горизонтальную конкатенацию матриц
- «$ | «Представляет вертикальную конкатенацию строкового массива
- « $ ~ »представляет горизонтальную конкатенацию строкового массива.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.


 Затем полученное число округляется до ближайшего возможного значения типа
Затем полученное число округляется до ближайшего возможного значения типа 
 Сколько она потратила?
Сколько она потратила? 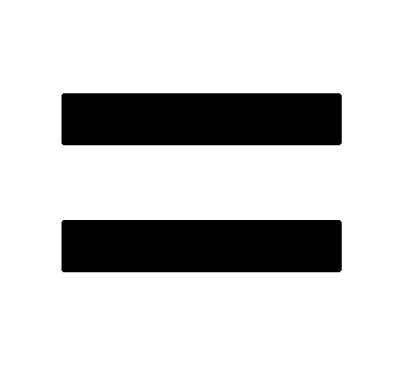 Сколько она потратит (без использования кредита)?
Сколько она потратит (без использования кредита)?