Знак равенства — Википедия
Материал из Википедии — свободной энциклопедии
Символы со сходным начертанием: 二 · ニ · ═ · ꞊| Знак равенства | |
|---|---|
| = | |
Изображение
| |
| equals sign | |
| Юникод | U+003D |
| HTML-код | |
| UTF-16 | 0x3D |
| %3D | |
Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя идентичными по своему значению выражениями.
Знак равенства в современной форме создал математик Роберт Рекорд (Robert Recorde, 1510—1558) в своём труде The Whetstone of Witte (1557). Он обосновал применение двух параллельных штрихов так (орфография оригинала — ранненовоанглийский): «…bicause noe 2 thynges can be moare equalle», то есть «никакие другие две вещи не могут быть более равными». До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал, чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда.
Таблица математических знаков (символов) эквивалентности с кодами Unicode[править | править код]
 | Необходимо добавить символы: |
В языках программирования символ = чаще всего используется для операций сравнения и/или присваивания. В некоторых языках (например, Basic) символ используется для обеих операций, в зависимости от контекста. В языках C, PHP и т. п. = обозначает присваивание, равенство записывается как ==. В Perl, кроме того, операторы для сравнения строк отличаются от операторов для сравнения чисел, равенство строк проверяет eq. В Pascal, напротив, = обозначает равенство, присваивание обозначается :=.
| |
= — Знак равно (U+003D)
Начертание символа «Знак равно» в разных шрифтах
Описание символа
Знак равно (равенства) в математике, логике и других точных науках означает полную идентичность значений двух выражений. В нынешней форме его создал математик Роберт Рекорд в своём труде The Whetstone of Witte от 1557 года.
Знак равенства находится в разделе основная латиница, а другие похожие символы (больше или равно ≥, меньше или равно≤,≠) лежат в блоке математические операторы.
Этот текст также доступен на следующих языках: Deutsch;
Подробнее СкрытьКодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | 3D | 61 | 61 | 00111101 |
| UTF-16BE | 00 3D | 0 61 | 61 | 00000000 00111101 |
| UTF-16LE | 3D 00 | 61 0 | 15616 | 00111101 00000000 |
| UTF-32BE | 00 00 00 3D | 0 0 0 61 | 61 | 00000000 00000000 00000000 00111101 |
| UTF-32LE | 3D 00 00 00 | 61 0 0 0 | 1023410176 | 00111101 00000000 00000000 00000000 |
Наборы с этим символом:
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | ||
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
≠ — Не равный (U+2260)
Начертание символа «Не равный» в разных шрифтах
≠Ваш браузер
Описание символа
Не равный. Математические операторы.
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 89 A0 | 226 137 160 | 14846368 | 11100010 10001001 10100000 |
| UTF-16BE | 22 60 | 34 96 | 8800 | 00100010 01100000 |
| UTF-16LE | 60 22 | 96 34 | 24610 | 01100000 00100010 |
| UTF-32BE | 00 00 22 60 | 0 0 34 96 | 8800 | 00000000 00000000 00100010 01100000 |
| UTF-32LE | 60 22 00 00 | 96 34 0 0 | 1612840960 | 01100000 00100010 00000000 00000000 |
Наборы с этим символом:
≡ — Идентичный, тождество (U+2261)
Начертание символа «Идентичный, тождество» в разных шрифтах
≡Ваш браузер
Описание символа
Идентичный, тождество. Математические операторы.
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 89 A1 | 226 137 161 | 14846369 | 11100010 10001001 10100001 |
| UTF-16BE | 22 61 | 34 97 | 8801 | 00100010 01100001 |
| UTF-16LE | 61 22 | 97 34 | 24866 | 01100001 00100010 |
| UTF-32BE | 00 00 22 61 | 0 0 34 97 | 8801 | 00000000 00000000 00100010 01100001 |
| UTF-32LE | 61 22 00 00 | 97 34 0 0 | 1629618176 | 01100001 00100010 00000000 00000000 |
Наборы с этим символом:
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Алфавиты, в т.ч. греческий и латинский. Символы. Коды. Альфа, бета, гамма, дельта, эпсилон… / / Таблица научных, математических, физических символов и сокращений. Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. Поделиться:
| ||||
Как поставить знак приблизительно равно в в Word и Excel — 3 способа

На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа Word или Excel.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.
Оба варианта работают в Word, Excel и других офисных программах.
Вставка символа без клавиатуры
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
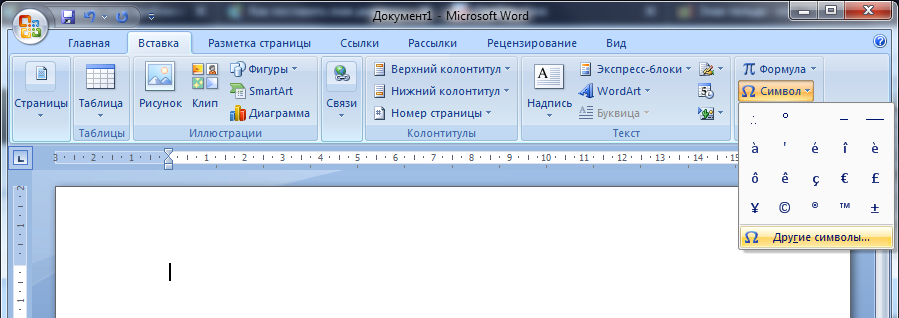
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
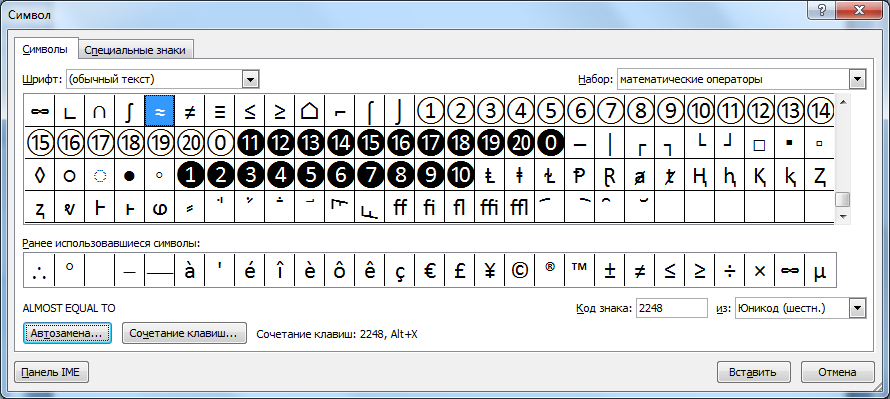
Похожие знаки равенства
Кроме знака примерного равенства есть много похожих математических и геометрических операндов. Они часто используются в формулах и имеют разную смысловую нагрузку.
| название | юникод | ASCII-код | |
|---|---|---|---|
| ≃ | гомеоморфизм | 2286 | 8788 |
| ~ | эквивалентность | 2286 | 8788 |
| ≅ | конгруэнтность | 2286 | 8788 |
К ним также применимы способы вставки в офисных программах.
Andy Si
26 февр. 2019 г.
8826

