Символ с в круге – Циркумпункт. Древняя солярная символика. Сакральная геометрия. Энергетические коды гармонии

Солнечный крест — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 октября 2018; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 октября 2018; проверки требуют 2 правки.

Со́лнечный крест, более известный, как Со́лнечное колесо́ — древнейший символ, представляющий собой крест, располагающийся внутри круга. Часто встречается на предметах доисторической Европы, особенно неолита и бронзового века.

С древнейших времён мотив Солнечного креста был распространён на Пиренеях, Армянском нагорье (см. аревахач), в Анатолии, Междуречье, Иране и Хараппской цивилизации.

В доисторической религии Европы бронзового века кресты в кругах часто появляются на артефактах, определяемых как культовые предметы, например «миниатюрный штандарт»

[уточнить] (англ. Miniature standard) с янтарной инкрустацией, в которой на просвет становится заметна форма креста, датируемый Северными бронзовым веком и находящийся в Национальном музее Дании в Копенгагене^[1].

Символы бронзового века также были связаны со спицами колеса колесницы, у которых в то время было четыре спицы (ср. идеограмму 243 «колесо» в линейном письме Б). Это технологическое новшество пришло в Европу в середине 2 тысячелетия до н. э.. У культур, имеющих представление о Солнечной колеснице, такое колесо приобретает солнечную символику.

В астрономии[править | править код]

В астрономии данный символ представляет Землю, тогда как Солнцу соответствует круг с точкой в центре.

В этнографии[править | править код]

В этнографии солнечный крест используется для представления индоевропейцев. Современные америнды и прочие народы традиционной культуры продолжают использовать Солнечный крест в качестве символа, орнамента и украшения.

В мифах[править | править код]

В осетинском нартовском эпосе солнечный крест символизирует колесо Балсага; по мнению ираниста Васо Абаева, это солярное оружие, восходящее к чудесному оружию Индры. По мифу, колесо Балсага было запущено его хозяином — Балсагом, по просьбе Сырдона, для убийства сильнейшего из нартов — Сослана. В первый раз колесо было схвачено Сосланом, но, обладая разумом, обратилось к нему с просьбой отпустить. Во второй раз оно застало Сослана спящим в лесу и переехало ему ноги. Сослан истёк кровью и умер. Батраз, солярный герой нартовского эпоса, названный сын Хурзарин — матери Солнца, и двоюродный брат Сослана (Сослан, помимо того, был мужем Ацырухс, девы башни, дочери Хурзарин), разыскал колесо Балсага и разломал его.

В музыке[править | править код]

В современной музыкальной табулатуре Солнечный крест может означать изменение для гитары с акустического тона к дисторшну^[2].

Норвежская нацистская партия «Национальное единение» (Nasjonal Samling) использовала золотой Солнечный крест на красном фоне в качестве своего официального символа с 1933 по 1945 год. Крест в круге отсылал к святому Олафу, покровителю Норвегии, а цвета представляют герб Норвегии.

Различные белые националистические и неонацистские группировки используют Солнечный крест в качестве символа белой расы^{[источник не указан 2716 дней]}. Также Солнечный крест нередко используется в качестве символа неоязычниками^{[источник не указан 2716 дней]}.

• Абаев В. А. Нартовский эпос. Орджоникидзе, 1945.

Что означает звезда в круге: в христианстве, в оккультизме

Пятиконечная звезда в круге — один из старейших символов. Самые старые пентаграммы находили при раскопках в древнем Шумере, Египте, Греции и Китае. Пентакль более 3,5 тыс. лет до н. э. был символом охраны, защиты. Служил также печатью для можновладцев. Существует множество заблуждений, связанных с трактовкой символа. В основном они возникли по причине религиозных воен. Широко используется в готической субкультуре, в официальной церкви Сатаны, в неоязычестве. Это известный математический и астрономический знак, неоценимо полезный в науке.

Разнообразие в изображении символа

Звезда, помещенная в круг — это пентаграмма или пентакль. Встречается в религиозной символике народов мира. Множество изображений модифицированы: в центре часто помещены такие знаки, как кельтский крест, козел Антиох, человек. Круги бывают одинарными или двойными. У славян пентаграмма украшена растительным орнаментом по орбите круга и цветочным внутри.

Если знак нарисовать, не отрывая карандаша от бумаги, он приобретает магический смысл.

Вернуться к оглавлению

Значение пятиконечной звезды

В совокупности они означают вечность. Пентаграмму еще и ассоциируют с 5 чувствами: зрение, слух, нюх, осязание, вкус. Астрологически ассоциируется с 5 планетами: Юпитер, Марс, Сатурн, Меркурий и Венера. Каждый луч символа характеризует стихию:

Каждый из углов знака имеет связь с определенной стихией.

• огонь, представляющий храбрость и смелость;
• воду — эмоции и интуиция;
• землю — стабильность и физическую силу;
• воздух — интеллект и искусство;
• спирит или дух — Божественное Божество и Все Сущее.

Вернуться к оглавлению

Древние времена и средневековье

Древние ученые наделяли звезду могуществом и властью, при этом считалось, что символ способен помогать и защищать. Поэтому часто наносили знак на амулеты, двери домов. Средневековые монахи Хильдегарды придавали пентаграмме божественное значение, поэтому нередко внутрь помещали фигуру человека. Позже в труде К. Агриппоя «Оккультная философия» была изложена теория «микрокосма», согласно которой пентакль стал символом духовной работы человека в окружающем мире. В дальнейшем трактовка знака сводилась больше к магическому и алхимическому значению.

Вернуться к оглавлению

В христианстве

Острый конец звезды, направленный вверх, символизирует переход материального в духовное, а идущий вниз — воплощение духа в теле. В раннем христианском пентакль символизировал духовную защиту, а позже стал характеризовать 5 ран Христовых. В пентакль также вкладывали имя Иисуса, на иврите — Иешуа. Знак помещали на гербы, одеяний священнослужителей, использовали для декорирования стен и окон храмов. Ярким примером служит Петербургский Храм Спаса на Крови. Но постепенно пентаграмма стала критиковаться христианами-фундаменталистами. Церковь в конечном итоге выбрала крест как более важный символ христианства, использование пентаграммы как христианского символа прекращено.

Вернуться к оглавлению

В оккультизме

Печать Бафомета – обязательный атрибут любого сатанинского обряда.

Сатанисты официально используют в своих ритуалах перевернутую звезду, печать козлоподобного идола Бафомета. Такая пентаграмма означает преисподнюю, где обитают падшие ангелы, а ее лучи символизируют хаос и не содержат духовной силы. Направленный пик звезды вниз указывает на преобладание темных сил над светлыми, зла над добром.

Вернуться к оглавлению

Печать Соломона

Первое изображение имеет вид звезды, направленной вверх пиковым лучом и заключенной в круг. Есть легенда, что могущественный маг преподнес в дар царю, после чего он успешно правил израильтянами. Силой печати Соломон сковал 72 демонов, заточенные, они служили царю. Амулет привлекает богатство, приносит победу в сражениях, укрепляет физическое и ментальное здоровье. Значение символа меняется с количеством углов фигуры в круге. Кулон магический пентакль Соломона помогает в торговле, предостерегает от неразумной траты денег. Носящему печать не навредит оружие или мрак темных сил, но откроются тайны миров.

Циркуль и наугольник — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 июня 2016; проверки требуют 25 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 июня 2016; проверки требуют 25 правок. Циркуль и наугольник с буквой G

Циркуль и наугольник (или, вернее, стальной циркуль и наугольник, соединённые вместе) являются самым узнаваемым символом масонства. Вместе, и циркуль и наугольник, как инструменты архитекторов, используются в масонских ритуалах, как эмблема обучения символическим урокам. Некоторые ложи и ритуалы объясняют эти символы, как уроки поведения: например, что масоны должны с помощью наугольника

ограничивать свои действия и циркулем учиться очерчивать и удерживать себя в пределах всего человечества^[1]. Поскольку масонство является не догматическим, то и не существует общей интерпретации этих символов (или любого масонского символа), которые используются масонством в целом^[2].

Как измерительные приборы, инструменты представляют собой суждения и умение распознавать^[3].

В английских юрисдикциях говорят, что циркули и наугольники часто изображаются с буквой «G» в центре. Такое написание интерпретируется для представления различных значений этого слова в разных юрисдикциях. Среди наиболее широко распространённых интерпретаций, что: «G» обозначает Бога (англ. God) и, чтобы напомнить масонам, что Бог находится в центре масонства. В этом контексте он также может быть представлен как Великий Архитектор Вселенной. В другом контексте написание представляет букву «G» как геометрию (англ. Geometry), описывая её как «благороднейшую из наук», и как «основу, на которой возведена надстройка масонства»

[4]^[3].

• Curl, James Stevens. The Art and Architecture of Freemasonry (неопр.). — New York: Overlook Press (англ.)русск., 1991.
• Domenico V., Ripa Montesano. Vademecum di Loggia (неопр.). — Roma Italia: Edizione Gran Loggia Phoenix–, 2009-ISBN 978-88-905059-0-4.

Религиозные символы — Википедия

Религиозные символы

Наиболее распространенные символы, ассоциирующиеся с Верой Бахаи, — девятиконечная звезда (девять — священное число), символ Наивеличайшего Имени и «Символ на перстне» (Ringstone symbol). Формально символом Веры Бахаи является пятиконечная звезда^[1].

Символ буддизма — Дхармачакра, или Колесо закона . Центр колеса — ступица, символизирует светящуюся точку сознания, излучающую душевный свет. Восемь спиц — символизируют суть буддийского учения, заключающуюся в следовании восьми «благородным принципам»:

• правильное воззрение,
• правильное мышление,
• правильная речь,
• правильное поведение,
• правильный образ жизни,
• правильное усилие,
• правильное осознание,
• правильное созерцание (концентрация внимания на внутреннем состоянии сознания).

Символ Инь и Ян. Инь — чёрное, женское, акцент на внутреннее; Ян — белое, мужское, акцент на внешнее.

Символ зороастризма — фаравахар — крылатый диск с верхней частью тела человека. Означает Божественное Благословение. По одной из версий — Царская Слава, Сияющая Слава. Также использовался в Древнем Египте, Месопотамии и у других народов Востока.

Символом индуизма является квинтэссенция слова «Ом» или «Аум» — универсальное имя Бога, три буквенных знака которого олицетворяют трёх главных богов и сферу их действия — Создание, Поддержание и Разрушение, а также отождествляют три состояния сознания — пробуждение, медитационное погружение и глубокий сон.

Символ ислама — полумесяц и пятиконечная звезда. В главе «Вафиятуль-Асляф» из книги «Таротибуль-идария» шейх Абдуль-Хайй аль-Катани пишет: «Установка знака в виде полумесяца над минаретами мечетей является бидъа. Данный знак был введен в обиход в эпоху правления османидской династии в Халифате, который они, в свою очередь заимствовали от цезарей Византии. История появления этого символа уходит корнями к одному из предков Александра Македонского, который со своим войском осадил город Байзанта (Константинополь). Жители же его в одну из ночей умудрились дать ему отпор и изгнать из города. Эта их победа совпала с появлением зари. Они сочли это добрым предзнаменованием и приняли символ в виде полумесяца в качестве увековечивания в памяти этого знаменательного события. Так этот символ по наследству перешел к цезарям (впоследствии ставшие императорами Византии — Константинополя), а после них Османидам, которые одержали победу над ними, позже этот символ появился в Российском городе Казани (Татарстан)». «Таротибуль-идария» 1/320

[2].

Символ иудаизма — это шестиконечная звезда (Звезда Давида).

Символом иудаизма также является храмовый светильник — менора^[3].

Один из древнейших сложных мистических символов — пентаграмма — правильная пятиугольная звезда. Первые упоминания о пентаграмме относятся к Древней Греции. В переводе с греческого «пентаграмма» означает дословно пять линий. Пентаграмма была отличительным знаком школы Пифагора (около 580—500 года до нашей эры). Они считали, что этот красивый многоугольник обладает многими мистическими свойствами. Например, число лучей этой звезды представлялось пифагорейцами как число любви: 5 = 2 + 3; 2 — первое женское число, 3 — первое мужское число. Именно поэтому пентаграмма являлась символом жизни и здоровья, ей присваивалась способность защищать человека от злых духов. Пентаграмма считалась защитой против зла и колдовства. В средние века её рисовали перед входом в дом и на дверях, чтобы отогнать таким образом зло. Пентагон (пятиугольник) — это амулет здоровья, символ вечности и совершенства, магическое средство в заговорах и некоторых ритуалах. Правильный пятиугольник в виде звезды служил эмблемой многих богов: египетского Тота, ацтекского Кетцалькоатля, римского Меркурия, кельтского Гавайна

[источник не указан 779 дней]… Этот знак был тотемом американских индейцев^{[источник не указан 779 дней]}. Греки использовали его как знак креста, евреи — как знак благополучия^{[источник не указан 779 дней]}. У христиан он символизировал пять ран Иисуса, а японцам служил знаком высокого положения в обществе.

Судя по всему^{[источник не указан 779 дней]}, пентаграмма первоначально появилась четыре тысячи лет назад в Месопотамии, вероятно как астрономическая схема движения планеты Венеры. Она стала шумерским и египетским знаком звезд. Эта фигура обозначает преимущественно человека: верхняя точка — голова, четыре остальные — конечности. Иногда её рассматривают как изображение пяти чувств. Светлые маги, чтобы действовать на духов, пользовались Пентаграммой головой кверху, а чёрные маги чертят Пентаграмму головой вниз. Фауст нарисовал пентаграмму для того, чтобы Мефистофель не смог переступить порог его дома ^[4]. Пентаграмма, вписанная в круг, означала у пифагорейцев молчание посвящаемого. Пять концов пентаграммы символизировали пять лет молчания и учения, которые предшествовали посвящению.

Сейчас её используют некоторые «забытые» религии (не являющиеся оккультными), основанные на магии и почитании природы.

Символ сикхов называется «кханда». Он составлен из трёх церемониальных кинжалов «кирпан», собранных вместе у рукояти и стального браслета «кара», расположенного за средним кинжалом.

«Форма последнего [креста в виде двух балок] произошла из древней Халдеи и употреблялась как символ бога Таммуза (в форме мистического Тау, первой буквы его имени)…….»

На первых порах знаком христианства было изображение рыбы. Рыба по старо-гречески — ἰχθύς («ихтис (ихтюс)»), что соответствует аббревиатуре христианского постулата «Ἰησοῦς Χριστός, Θεοῦ Υἱός, Σωτήρ» (ΙΧΘΥΣ) — «Иисус Христос — Божий Сын Спаситель».

Православный крест. К большой горизонтальной перекладине были пригвождены руки Спасителя Иисуса Христа. Верхняя малая горизонтальная перекладина означает табличку, на которой было начертано «Иисус Назорей Царь Иудейский». Косая перекладина означает двух распятых рядом с Христом, где конец перекладины, направленный вверх, означает прощёного разбойника, который попал в рай, а конец перекладины, направленный вниз — второго распятого, который попал в ад. По другой версии, косая перекладина показывает упор для ног приговоренного в перспективе, который не давал распятому умереть сразу и применялся для увеличения времени казни.

В католицизме используется четырёхконечная форма креста с удлинением нижней части. Кроме того, в отличие от православного креста, на нём ступни Христа скрещены и забиты одним гвоздём.

Печать Бафомета — официальный символ Церкви Сатаны. Являет собой перевернутую пентаграмму (правильную пятиконечную звезду, два луча которой направлены вверх) с вписанной в неё головой козла. В кольцо вокруг пентаграммы, напротив каждого луча звезды, вписано имя «Левиафан» (ивр. ‏לִוְיָתָן‏‎). Либо может использоваться только перевернутая пентаграмма, которая известна как Сатанинский символ с XIX века^[5].

1. ↑ См. письмо Хранителя одному верующему от 28 октября 1949: U.S. Supplement to Baha’i News, No. 50, p. 4, April 1962. Цитируется по Lights of Guidance: A Baha’i Reference File п.375
2. ↑ Есть ли символ у Ислама?
3. ↑ Курганова У. Иудаизм. — Directmedia, 2014. — 154 с. — ISBN 9789660355675.
4. ↑ (см. Гёте. Фауст)
5. ↑ Ричард Кавендиш, Чёрная Магия Пер. с англ. А. Блейз. — М.: ТЕРРА-Книжный клуб, 2000. — 416 с. — (По ту сторону). ISBN 5-275-00087-1

Окружность — Википедия

Окружность (C), её центр (O), радиус (R) и диаметр (D)

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки^[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части^[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Построение окружности циркулем

Практическое построение окружности возможно с помощью циркуля.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква R{\displaystyle R} обозначает радиус окружности.

Прямая может иметь с окружностью не более двух общих точек.

Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды^[3].

Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)^[3].

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства^[3].

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

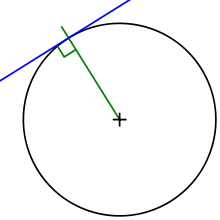
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности^[4].

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности^[5].

• 

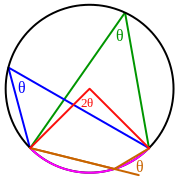
  Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

• 

  К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением^[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsin⁡θ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

• Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
• Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.

• Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.

AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED} Если радиус круга равен 1, то его окружность равна 2π.

Длина окружности:

C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}

Радиус окружности:

R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}

Диаметр окружности:

D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}

Площадь круга радиуса R:

S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

S=πR2α360∘−R2sin⁡α2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Аналитическая геометрия окружностей[править | править код]

С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.

Декартовы координаты[править | править код]

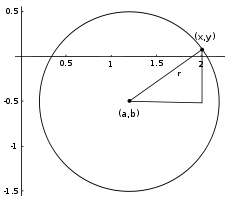Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}

или

(x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}

где

2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}

Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.

Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:

x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}

Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):

|x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}

Тогда в явном виде координаты центра окружности определяются по формулам:

x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

Окружность также можно описать с помощью параметрического уравнения:

{x=x0+Rcos⁡φy=y0+Rsin⁡φ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}

Если центр окружности совпадает с началом координат, функции принимают вид:

y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}

Полярные координаты[править | править код]

Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:

ρ2−2ρρ0cos⁡(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}

Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:

ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}

Если же центр является началом координат, то уравнение будет иметь вид

ρ=R.{\displaystyle \rho =R.}

Комплексная плоскость[править | править код]

На комплексной плоскости окружность задаётся формулой:

|z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}

или в параметрическом виде

z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}

Окружности в пространстве[править | править код]

В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы

(x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}

плоскостью

a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},

где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы

{(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0.{\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}

Например, при a=c≠0{\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:

{x=x0+Ra2+c2⋅(c⋅cos⁡t−a⋅b⋅sin⁡ta2+b2+c2),y=y0+R⋅a2+c2a2+b2+c2⋅sin⁡t,z=z0−Ra2+c2⋅(a⋅cos⁡t+b⋅c⋅sin⁡ta2+b2+c2),t∈[0;2π).{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}

Касательные и нормали[править | править код]

Уравнение касательной к окружности в точке (x1,y1){\displaystyle \left(x_{1},y_{1}\right)} определяется уравнением

(A2+x1)x+(B2+y1)y+(A2x1+B2y1+C)=0.{\displaystyle \left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.}

Уравнение нормали в той же точке можно записать как

x−x12x1+A=y−y12y1+B.{\displaystyle {\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.}

Концентрические и ортогональные окружности[править | править код]

Концентрические окружности

Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:

x2+y2+A1x+B1y+C1=0,x2+y2+A2x+B2y+C2=0{\displaystyle x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0}

являются концентрическими в том и только в том случае, когда A1=A2{\displaystyle A_{1}=A_{2}} и B1=B2.{\displaystyle B_{1}=B_{2}.}

Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие

A1A2+B1B2=2(C1+C2).{\displaystyle A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).}

Что означает этот символ? (Буква А в круге)

«Анархия — мать порядка» <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Анархистская_символика» target=»_blank»>http://ru.wikipedia.org/wiki/Анархистская_символика</a> Символ А-в-круге можно встретить еще в книге Штефана Михельспахера (Stephan Michelspacher) Spiegel der Kunst und Natur (Зеркало искусства и природы) , опубликованной в Аусбурге в 1615 г. Эта была работа по алхимии, написанная под влиянием взглядов Агриппы на Каббалу и магию. Адам МакЛин описывает центральную часть рисунка как «две диаграммы с немецким GOTT (Бог) , расположенным по углам и буквами альфа и омега, а также монограммой, которая может означать имя Бога, Agla. Это означает начало — альфу, и конец — омегу (первую и последнюю буквы греческого алфавита) и восходит к Книге Откровения, где говорится, что Иисус есть «Альфа и Омега, Начало и Конец, Первый и Последний» (22:13).

Так это же анархия…. Анархия-мать порядка!!!!

сатанинский символ

Анархия это. Символ панков.

Да, это панковский значёк. Но раньше это был знак падшей женщины, которая родила внебрачного ребёнка. К примеру посмотрите фильм «Алая буква» с Деми Мур и Гэри Олдманом. Ну конечно знак немного не тот, но там тоже бувка «А» в кружке)

Ахах убили ответы про панков и станаизм) А на самом деле серъезно. А значит Анархия

Это знак готов. Рисуется тёмно-синей, чёрной и красной краской. У меня во дворе таких полно!!!

Ограниченно употреблявшийся в 1960-1970-е годы в американской типографике экспериментальный знак препинания: лигатура, представляющая собой наложение вопросительного и восклицательного знаков. АНАРХИЯ мать порядка=3

Это означает — сколько ты видишь треугольников? )))

А в круге — определённо, самый известный на сегодняшний день символ анархии. Это монограмма, которая состоит из заглавной буквы «А», окруженной заглавной буквой «O». Буква «А» происходит от начальной буквы слов «анархия» и «анархизм» в большинстве европейских языков, которая одинаково выглядит как в латинском шрифте, так и в кириллице. Буква «О» означает «порядок». Вместе они означают «Анархия — мать порядка» — знаменитую фразу Прудона. Код Unicode для этого символа — U+24B6 Ⓐ. Также используются версии (A) и @. Доанархистское использование [править | править вики-текст] Иллюстрация из книги Spiegel der Kunst und Natur, 1615. Символ А-в-круге можно встретить еще в книге Штефана Михельспахера (Stephan Michelspacher) Spiegel der Kunst und Natur (Зеркало искусства и природы), опубликованной в Аусбурге в 1615 г. Эта была работа по алхимии, написанная под влиянием взглядов Агриппы на Каббалу и магию. Адам МакЛин описывает центральную часть рисунка как «две диаграммы с немецким GOTT (Бог), расположенным по углам и буквами альфа и омега, а также монограммой, которая может означать имя Бога, Agla.» Это означает начало — альфу, и конец — омегу (первую и последнюю буквы греческого алфавита) и восходит к Книге Откровения, где говорится, что Иисус есть «Альфа и Омега, Начало и Конец, Первый и Последний» (22:13). История анархистского использования [править | править вики-текст] А в круге. Панк-стиль Впервые А-в-круге было использовано Федеральным Советом Испании Международной Рабочей Ассоциации (1-й Интернационал). Позже этот символ использовался во время гражданской войны в Испании. Сохранилась фотография анархиста из «ударной группы», на обратной стороне чьего шлема чётко изображено «А в круге». Позже этот символ был перенят Брюссельской организацией Alliance Ouvriere Anarchiste (АОА) 25 ноября 1956 года, а ещё позже — французской организацией Jeunesse Libertaire («Либертарная Молодёжь») в 1964 году. Особенно известным символ стал в середине 1970-х годов с развитием панк-движения. Именно панк-культура понесла символ «в массы», немного изменив его: буква А выходит за рамки круга. Поэтому многие анархисты избегают использовать этот символ, так как считают, что он ассоциируется прежде всего с панк-культурой, а не с серьёзной анархической идеологией и более коммерциализирован. Анархистский чёрный крест [править | править вики-текст] Анархистский чёрный крест Главной задачей организации «Анархистский чёрный крест» является ликвидация всех тюрем. Она впервые возникла в царской России как организация, поддерживающая политических заключённых. Их символом является чёрный крест, увенчанный сжатым кулаком, символом, также связанным с анархизмом, отрицанием власти. Кулак также означает союз, так как «слабые пальцы, объединяясь, образуют сильный кулак». Крест является модификацией эмблемы Красного Креста, используемой Международным Комитетом Красного Креста, крупнейшей мировой гуманитарной организацией. Изначально называясь «Анархистский красный крест», организация изменила своё название в 1919, чтобы избежать путаницы с Международным Комитетом Красного Креста, который тоже начал работу по освобождению заключённых.

ⓥ — Латинская строчная буква v в круге (U+24E5)

Описание символа

Латинская строчная буква v в круге. Вложенные буквы и цифры.

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	E2 93 A5	226 147 165	14848933	11100010 10010011 10100101
UTF-16BE	24 E5	36 229	9445	00100100 11100101
UTF-16LE	E5 24	229 36	58660	11100101 00100100
UTF-32BE	00 00 24 E5	0 0 36 229	9445	00000000 00000000 00100100 11100101
UTF-32LE	E5 24 00 00	229 36 0 0	3844341760	11100101 00100100 00000000 00000000

Наборы с этим символом: