Сложный план что это: План текста — виды (простой, сложный тезисный)

Могли бы придумать менее сложный план, ну да ладно.

Могли бы придумать менее сложный план, ну да ладно.

Suggest an example

Возможно это все часть сложного плана.

Ну да, ну да, мы случайно столкнулись друг с другом.

Еще один сложный план побега для ребенка, только что выросшего из пеленок.

Поистине, это сложный план работы, однако Организация не должна уклоняться от его выполнения.

I would also like to convey to all present my pride regarding the tenth anniversary of my country’s independence.

Наверняка, есть более сложный план, раз он хочет отвлечь от расследования мою группу.

Это был амбициозный и сложный план.

Всё это — часть моего сложного плана победы над вами.

Всё это может быть сложным планом, заставить нас отключить червоточину, чтобы больше кораблей Орай вошли в нашу галактику.

Поистине, это сложный план работы, однако Организация не должна уклоняться от его выполнения.

Структурное обследование предприятий в Латвии опирается на довольно сложный план формирования выборки, состоящий из ряда перечней респондентов.

С этой целью он, возможно, разработал сложный план с использованием фирмы «Ваксом» и счетов в швейцарских банках.

Ну да, давняя семейная традиция.

Ну да, четырехчасового разглагольствования по дороге сюда было недостаточно.

Ну да ладно, ты наверняка думал о…

Ну да, обычно поскальзываешься, когда тебя бьют по башке.

Мы спорили.Я вспыльчивый.А ну да конечно.

Ну да, разумеется, милорд.

Ну да, такая возможность существовала.

Как написать план на ЕГЭ по обществознанию на максимальный балл

Многие выпускники называют ЕГЭ по обществознанию одним из самых сложных экзаменов в 11-м классе. Наш блогер, репетитор по обществознанию Алексей Соловьёв, помогает выпускникам готовиться и объясняет, как написать 28-е задание из ЕГЭ по обществознанию.

Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу

Одним из самых сложных заданий для сдающих ЕГЭ по обществознанию является составление планов (это задание в тестах под номером 28 и за него дают четыре первичных балла). В описании к нему даны условия, соблюдение которых является залогом успешного выполнения.

Как правильно составлять план и что нужно знать об этом?

Итак, план называется сложным, потому что он имеет пункты и подпункты, то есть структура должна выглядеть так:

1.

2.

2.1

2.2

2.3

3.

3.1

3.2

3.3

Что значит «раскрыть по существу»? Это означает, что вы должны осветить все важные (существенные) аспекты разбираемой темы и отразить их в сложном плане, состоящем из пунктов и подпунктов по схеме, представленной выше.

В задании сказано, что пунктов должно быть минимум три (можно и больше, но не меньше), а в пунктах с подпунктами не менее трёх подпунктов. То есть перечисляя какие-то характеристики, виды, критерии, признаки, функции, вы должны упомянуть минимум три подпункта (за исключением если их всего два, например, видов избирательного права или уровней научного познания всего по два, в принципе).

Разберём на конкретном примере

Как составлять план, учитывая все упомянутые требования? У вас есть общая схема, которую нужно заполнить конкретным содержанием по теме. Будем рассуждать.

Я — сторонник логического рассуждения и построения умозаключений при опоре на базовую информацию по теме. Так не нужно будет механически «запихивать» в голову весь огромный объём информации по курсу.

Тема «Политические партии»

Даже скромные познания позволят вам определить раздел, из которого нужно взять информацию для составления плана. Это политическая сфера и, соответственно, речь идёт о политике, власти, политических институтах и так далее. В самом названии присутствует множественное число, что даёт подсказку о существовании нескольких политических партий, а значит один пункт с подпунктами уже намечен — «Типы политических партий».

Раз партия — это какое-то особое явление, то у нее будут специфические признаки или характеристики, а значит ещё один развернутый пункт — «Признаки политической партии».

И, наконец-таки, раз политическая партия существует и играет какую-то роль в общественной жизни, то значит у неё есть какие-то функции. Получился ещё один развернутый пункт с подпунктами — «Функции политических партий».

Чаще всего признаки, виды (типы) и функции образуют триаду для составления сложных планов к большинству тем

Какую бы тему вы не взяли, будет ли это «Семья как малая группа» или «Предпринимательская деятельность», вы сможете выделить признаки, виды и функции этого общественного явления или института. Это не всегда работает, но чаще всего это именно тот ориентир, который поможет составить сложный план и успешно выполнить 28 задание.

Зачем ещё может пригодиться составление планов?

Фактически весь курс обществознания (если вы откроете любой учебник по обществознанию или справочник Баранова) представляет собой один большой сложный план по всем разделам и темам из курса. Вам нужно представлять весь необходимый материал для сдачи ЕГЭ по обществознанию в виде планов. Чтобы вы не писали или запоминали, то вам нужны:

• Определения понятий;
• Критерии (признаки), виды, функции;
• Понимание связи темы с разделом и её местом в курсе обществознания в целом.

Это своего рода программа минимум, опираясь на которую вы можете с уверенностью расширять свои познания и не утонуть в море информации по курсу обществознания. Именно сложные планы будут помогать вам увереннее писать эссе (минисочинение) по обществознанию и быть опорой при выполнении любых других типов заданий.

Успехов всем, кто сдаёт ЕГЭ по обществознанию в 2020 году!

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Фото: Unsplash (Clark Young)

Презентация «Простой и сложный план»

Слайды и текст этой онлайн презентации

Слайд 1

Слайд 2

ПОВТОРЯЕМ ОРФОГРАФИЮ

Слайд 3

Слайд 4

ОРФОГРАФИЧЕСКАЯ РАЗМИНКА
В левый столбик выпишите слова с проверяемыми безударными гласными в корне, в правый – с непроверяемыми. Подчеркните безударную гласную корня.
Н..винка, г..товить, м..стечко, д..леко, м..нута, нак..рмить, к..мандир, р..совать, д..лина, м..лина, п..мидоры, н..зина, б..рега, к..ртошка, к..лендарь.

Слайд 5

ПРОВЕРЯЕМ!
НОвинка мЕстечко дАлеко накОрмить дОлина нИзина бЕрега
ГОтовить мИнута кОмандир рИсовать пОмидоры мАлина кАртошка кАлендарь

Слайд 6

ПРОСТОЙ И СЛОЖНЫЙ ПЛАН

Слайд 7

ЦЕЛИ УРОКА:
формировать навыки определения основной темы текста и микротем текста; учить разделять текст на смысловые части; совершенствовать навыки формулировки микротем; познакомить с понятиями простой и сложный план; научить составлять простой и сложный план к тексту.

Слайд 8

АКТУАЛИЗАЦИЯ ЗНАНИЙ
ЧТО ТАКОЕ ПЛАН К ТЕКСТУ? ИЗ КАКИХ ПРЕДЛОЖЕНИЙ МОЖЕТ СОСТОЯТЬ ПЛАН? ДЛЯ ЧЕГО НУЖЕН ПЛАН?

Слайд 9

РАБОТА С УЧЕБНИКОМ
УПРАЖНЕНИЕ №14

Слайд 10

РАБОТА С УЧЕБНИКОМ
СТР.16-17, I, II, III.

Слайд 11

РАБОТА С УЧЕБНИКОМ
УПРАЖНЕНИЕ №16

Слайд 12

ПАМЯТКА
ФОРЗАЦ УЧЕБНИКА № I

Слайд 13

РАБОТА С ТЕКСТОМ
ПРОЧИТАЙТЕ ОПРЕДЕЛИТЕ ТЕМУ И ОСНОВНУЮ МЫСЛЬ РАЗДЕЛИТЕ ТЕКСТ НА МИКРОТЕМЫ СОСТАВЬТЕ СЛОЖНЫЙ ПЛАН ТЕКСТА

Слайд 14

РЕФЛЕКСИЯ
ПЛАН – ЭТО…. ДЛЯ ЧЕГО НУЖЕН ПЛАН? КАКИМ МОЖЕТ БЫТЬ ПЛАН? В ЧЕМ ОТЛИЧИЕ ПРОСТОГО ОТ СЛОЖНОГО ПЛАНА?

Слайд 15

ДОМАШНЕЕ ЗАДАНИЕ
2, выучить теорию; упражнение № 20 задание № 1,3; повторить правописание безударных гласных и правописание Ь

Слайд 16

СПАСИБО ЗА РАБОТУ!

Сложный самолет

	Нет, не эта комплексная плоскость . ..
… это комплексная плоскость :	A самолет для комплексных номеров !

(Также называется «диаграммой Аргана»)

Реальное и воображаемое составляют комплекс

Комплексное число — это комбинация действительного и мнимого числа:

Реальный номер — это тип номера, который мы используем каждый день.

Примеры: 12,38, ½, 0, −2000

Когда мы возводим в квадрат действительное число, мы получаем положительный (или нулевой) результат:

2 ² = 2 × 2 = 4
1 ² = 1 × 1 = 1
0 ² = 0 × 0 = 0

Что мы можем возвести в квадрат, чтобы получить −1?

? ² = -1

Возведение в квадрат −1 не работает, потому что умножение отрицательных чисел дает положительное значение: (−1) × (−1) = +1, и никакое другое действительное число также не работает.

Значит математика кажется неполной …

… но мы можем заполнить пробел на , представив , есть число, которое при умножении само на себя дает −1
(назовем его i для мнимого):

и ² = -1

И вместе:

Комплексное число — это комбинация действительного и мнимого числа

Примеры: 3,6 + 4 i , −0,02 + 1,2 i , 25-0.3 i , 0 + 2 i

Отображение комплексного числа на плоскости

Возможно, вам знакома числовая строка:

Но где мы помещаем комплексное число вроде 3 + 4 i ?

Пусть линия вещественных чисел идет влево-вправо, как обычно, а линия мнимых чисел идет вверх и вниз :

А это комплексная плоскость :

• комплексный , потому что это комбинация действительного и мнимого,
• плоскость потому что она похожа на геометрическую плоскость (2-х мерную).

Весь новый мир

Теперь давайте перенесем идею о плоскости (декартовы координаты, полярные координаты, векторы и т. Д.) В комплексные числа.

Он откроет совершенно новый мир чисел, более полных и элегантных, как вы увидите.

Комплексное число как вектор

Мы можем думать о комплексном числе как о векторе.

Это вектор.
Имеет величину (длину) и направление.

Добавление

Вы также можете складывать комплексные числа как векторы:

Полярная форма

Таким образом, комплексное число 3 + 4i также может отображаться как расстояние (5) и угол (0.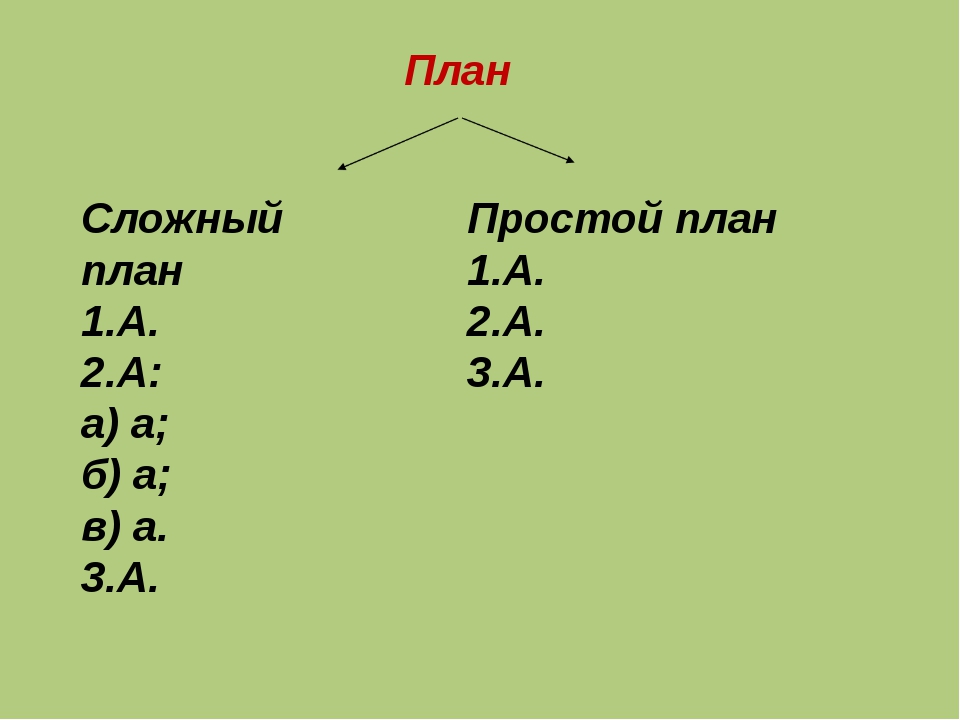 927 радиан).

Давайте посмотрим, как преобразовать из одной формы в другую, используя преобразование из декартовой системы координат в полярную:

Пример: номер

из 3 + 4i :

• r = √ (x ² + y ² ) = √ (3 ² + 4 ² ) = √25 = 5
• θ = tan ^-1 (y / x) = tan ^-1 (4/3) = 0,927 (до 3 десятичных знаков)

И получаем расстояние (5) и угол (0.927 радиан)

Снова:

• x = r × cos ( θ ) = 5 × cos (0,927) = 5 × 0,6002 … = 3 (достаточно близко)
• y = r × sin ( θ ) = 5 × sin (0,927) = 5 × 0,7998 … = 4 (достаточно близко)

И расстояние 5 и угол 0,927 снова становятся 3 и 4

На самом деле, обычный способ записать комплексное число в полярной форме — это

x + i y = r cos θ + i r sin θ

= r (cos θ + i sin θ )

И «cos θ + i sin θ » часто сокращается до «cis θ », поэтому:

x + iy = r цис θ

cis — это просто сокращение для cos θ + i sin θ

3 + 4i = 5 цис 0. 927

В некоторых предметах, например в электронике, «цис» используется очень много!

Сводка

• Комплексная плоскость — это плоскость, на которой:
  • действительные числа слева направо и
  • мнимых числа, бегущих вверх-вниз.
• Чтобы преобразовать из декартовой в полярную форму:
  • r = √ (x ² + y ² )
  • θ = tan ^-1 (y / x)
• Чтобы преобразовать полярную форму в декартову:
  • x = r × cos ( θ )
  • y = r × sin ( θ )
• Полярная форма r cos θ + i r sin θ часто сокращается до r cis θ

Далее… узнать об умножении комплексных чисел.

комплексная плоскость, сложение и вычитание

Обозначение.

Мы попробуем использовать x и y для вещественных переменных и z и w для комплексных переменных. Например, уравнение z = x + yi следует понимать как говорящее, что комплексное число z является суммой действительного числа x и действительного числа y , умноженного на i. В общем, часть x комплексного числа z = x + yi называется действительной частью z , а y называется мнимой частью z . (Иногда yi называют мнимой частью.)

Когда мы используем плоскость xy для комплексной плоскости C , мы будем называть ось x именем действительной оси , и ось y мы назовем мнимая ось.

Вещественные числа следует рассматривать как частные случаи комплексных чисел; это просто числа x + yi , когда y равно 0, то есть это числа на действительной оси.Например, действительное число 2 — это 2 + 0 i. Числа на мнимой оси иногда называют чисто мнимыми числами.

Арифметические операции на

Сложение может быть представлено графически на комплексной плоскости C . Возьмем последний пример. Комплексное число z = 3 + i расположено на 3 единицы справа от мнимой оси и на 1 единицу выше действительной оси, а w = –1 + 2 i расположено на 1 единицу слева и 2 единиц вверх. Таким образом, сумма z + w = 2 + 3 i равна 2 единицам вправо и на 3 единицы больше.

Правило параллелограмма.

Дополнение как перевод.

Отрицание и вычитание.

Отрицание можно интерпретировать как преобразование плоскости C . Если повернуть плоскость на 180 ° вокруг 0, то каждая точка z отправляется в свое отрицание — z. Таким образом, отрицание дает поворот на 180 °.

Используя сложение и отрицание, вы можете определить геометрическое правило вычитания. Чтобы найти, где будет z — w , сначала инвертируйте w , найдя точку напротив 0, а затем используйте правило параллелограмма.

Мы можем интерпретировать вычитание w как преобразование C : плоскость перемещается по вектору от 0 до — w. Другими словами, плоскость перемещается по вектору w 0.

Нанести комплексные числа на комплексную плоскость

Мы не можем нанести комплексные числа на числовую линию, как действительные числа. Однако мы все еще можем изобразить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость , которая представляет собой систему координат, в которой горизонтальная ось представляет реальную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар ( a , b ), где a представляет координату для горизонтальной оси, а b представляет координату для вертикальной оси.

Рисунок 2

Рассмотрим число [латекс] -2 + 3i \\ [/ latex]. Действительная часть комплексного числа равна –2, а мнимая часть — 3 i . Мы строим упорядоченную пару [латекс] \ left (-2,3 \ right) \\ [/ latex], чтобы представить комплексное число [latex] -2 + 3i \\ [/ latex] .

Общее примечание: сложная плоскость

Рисунок 3

В комплексной плоскости горизонтальная ось является действительной осью, а вертикальная ось — мнимой осью .

Как: дано комплексное число, изобразите его компоненты на комплексной плоскости.

1. Определите действительную и мнимую части комплексного числа.
2. Переместитесь по горизонтальной оси, чтобы показать действительную часть числа.
3. Двигайтесь параллельно вертикальной оси, чтобы показать мнимую часть числа.
4. Обозначьте точку.

Пример 2: Построение комплексного числа на комплексной плоскости

Постройте комплексное число [латекс] 3 — 4i \ [/ латекс] на комплексной плоскости.

Решение

Действительная часть комплексного числа равна 3, а мнимая часть — –4 i . Строим упорядоченную пару [латекс] \ left (3, -4 \ right) \\ [/ latex].

Рисунок 4

Попробуй 2

Постройте комплексное число [latex] -4-i \\ [/ latex] на комплексной плоскости.

Решение

Как складывать комплексные числа в комплексной плоскости — видео и стенограмма урока

Как их сложить

С этой векторной формой и нашей комплексной плоскостью теперь мы можем очень легко складывать наши комплексные числа вместе. Все, что нам нужно сделать, это переместить один из наших векторов так, чтобы он начинался там, где заканчивается другой. Переместим синюю стрелку так, чтобы она начиналась там, где заканчивается красная стрелка.

Когда мы это сделаем, наш ответ — точка, на которую указывает синяя стрелка.Это (13, 2). Это дает нам комплексное число 13 + 2 i .

Мы также могли переместить красную стрелку так, чтобы она начиналась там, где заканчивается синяя стрелка. Когда мы это сделаем, красная стрелка укажет на наш ответ.

Рассмотрим еще пару примеров.

Пример 1

Складываем -6 + 10 i и 4 + 2 i .

Сначала мы наносим точки (-6, 10) и (4, 2) на нашу комплексную плоскость. Затем рисуем стрелки из начала координат.

Затем перемещаем одну из стрелок так, чтобы она начиналась там, где заканчивается другая.

Мы видим, что он указывает на (-2, 12). Итак, наш ответ — -2 + 12 i .

Пример 2

Складываем 1 + 3 i и 4 + 5 i

Здесь мы сделаем то же самое. Сначала мы наносим точки (1, 3) и (4, 5). Затем мы рисуем стрелки к каждому.

Затем перемещаем одну из стрелок так, чтобы ее начало соединилось с концом другой стрелки.

Мы видим синюю стрелку, указывающую на точку (5, 8). Это говорит нам, что ответ — 5 + 8 i .

Резюме урока

Давайте рассмотрим то, что мы узнали. Комплексное число — это число, имеющее как действительную, так и мнимую части. i означает мнимое и представляет собой квадратный корень из -1.

Чтобы сложить комплексные числа на комплексной плоскости, сначала наносим точки. Комплексное число — a + bi и строится в точке ( a , b ). Реальная часть сообщает нам, где она будет на действительной оси, а мнимая часть сообщает нам, где находится точка на мнимой оси. Комплексная плоскость такая же, как декартова плоскость, за исключением того, что у нее есть действительная ось для оси x и мнимая ось для оси y.Затем мы рисуем стрелки к каждому из начала координат, создавая их векторные формы. Затем, чтобы найти ответ, мы перемещаем одну стрелку так, чтобы ее начало находилось в конце другой стрелки. Где указывает наша стрелка, и есть наш ответ.

Краткий урок

Сложение комплексных чисел выполняется на комплексной плоскости, которая похожа на декартову плоскость. Комплексное число — это число, имеющее как действительную, так и мнимую части.

Стрелки, начинающиеся с начала координат, указывают на векторную форму комплексного числа.n $ к себе дифференцируем, если существует линейное преобразование $ J $ такое, что существует предел:

$$ \ lim_ {h \ to 0} \ frac {\ mathbf {f} (\ mathbf {x} + \ mathbf {h}) — \ mathbf {f} (\ mathbf {x}) — \ mathbf {J } \ mathbf {h}} {\ | \ mathbf {h} \ |} = 0 $$

где $ \ mathbf {f}, \ mathbf {x}, $ и $ \ mathbf {h} $ — векторные величины.

В $ \ mathbb {C} $ имеется более сильное понятие дифференцируемости, задаваемое уравнениями Коши-Римана:

$$ \ begin {align *} f (x + iy) & \ stackrel {\ textrm {def}} {=} u (x, y) + iv (x, y) \\ u_x & = v_y, \\ u_y & = -v_x.2 $ немного более «топологичен» — нас не слишком заботит, где находится $ \ mathbf {h} $, просто он становится маленьким и существует неособое линейное преобразование в точке дифференцирования. Все это проистекает из обобщения теоремы об обратной функции, к которой в принципе можно подойти полностью топологически.

В $ \ mathbb {C} $, поскольку мы можем делить на $ h $, поскольку у нас есть строгое понятие умножения и деления, мы хотим гарантировать, что производная существует независимо от пути, по которому идет $ h $.2 $.

PDST Математика после начального образования | Новые ресурсы: преподавание математики в среде DEIS

Этот веб-сайт использует Google Analytics для сбора анонимной информации, такой как количество посетителей сайта и наиболее популярные страницы.

Включение этого файла cookie помогает нам улучшать наш веб-сайт.

Пожалуйста, сначала включите строго необходимые файлы cookie, чтобы мы могли сохранить ваши предпочтения!

Показать детали

Имя	Провайдер	Цель	Срок действия
_ga	Google	Файл cookie Google Analytics, который используется для расчета данных о посетителях, сеансах и кампании, а также для отслеживания использования сайта в аналитическом отчете сайта.Файлы cookie хранят информацию анонимно и присваивают случайно сгенерированный номер для идентификации уникальных посетителей. Отказаться на странице https://tools.google.com/dlpage/gaoptout	730 дней
_gat	Google	Файл cookie Google Analytics, используемый для регулирования скорости запросов. Отказаться на странице https://tools.google.com/dlpage/gaoptout	1 день
_gid	Google	Файл cookie Google Analytics используется для хранения информации о том, как посетители используют веб-сайт, и помогает в создании аналитического отчета о том, как работает веб-сайт.Собранные данные, включая количество посетителей, источник, откуда они пришли, и страницы, посещенные в анонимной форме. Отказаться на странице https://tools.google.com/dlpage/gaoptout	1 день
NID	Google	Содержит уникальный идентификатор, который Google использует для запоминания ваших предпочтений и другой информации, например, предпочитаемого вами языка (например,грамм. Английский), сколько результатов поиска вы хотите отображать на странице (например, 10 или 20) и хотите ли вы, чтобы фильтр безопасного поиска Google был включен.

Генеральный план комплекса Капитолия | OSA

Годовое исследование зданий и территорий, принадлежащих и управляемых штатом Колорадо в районе Капитолия штата, и соответствующие рекомендации были опубликованы Управлением государственного архитектора в 2013 году.Утвержденный законопроектом Сената 13-263 (C.R.S. 24-82-101 (3)) Генеральный план комплекса Капитолия будет способствовать принятию решений по планированию, техническому обслуживанию и финансированию объектов посредством всесторонней оценки потребностей агентства, условий строительства и вопросов городского проектирования. С момента завершения генерального плана последнего объекта прошло более 25 лет.

Объем генерального плана включает 11 зданий и территорий в Capitol Buildings Group в комплексе Capitol, а также дополнительные здания и участки, принадлежащие Департаменту администрации и персонала (DPA) и управляемые Capitol Complex Applications (CCF) в столичном районе Денвера и одно здание, расположенное в Гранд-Джанкшен.

В план были внесены изменения в 2021 году новой Главой 9.

Генеральный план комплекса Капитолия может быть просмотрен лично в Государственном архиве Колорадо, 1313 Sherman St.

Все следующие документы откроются в новой вкладке .

Полный отчет (размер отпечатка 11 x 17 дюймов)
Генеральный план комплекса Капитолия (CCMP) (28 МБ)

Глав (размер печати 11 x 17 дюймов)

Краткое изложение и содержание (0.5 МБ)

1 — Введение (2,4 МБ)

2 — Обзор комплекса Capitol (2,1 МБ)

3 — Агентства (2,6 МБ)

4 — Оценка объекта (2,4 МБ)

5 — Городской дизайн (5,1 МБ)

6 — Бенчмаркинг (8,7 МБ)

7 — Рекомендации по генеральному плану (2,1 МБ)

8 — Варианты реализации / финансирования (3,6 МБ)

9 — Поправки 2-19-2021 (544 kB)

Приложения

Приложение 1 — Агентства (a) Обновленные исследования и (b) Таблица исходных данных (2. 2 МБ) (размер печати 8,5 x 11)

Приложение 2 — Городской дизайн (а) Анализ перекрестков и (б) Оценка мультимодальных перевозок (3,4 МБ) (размер шрифта смешанный, 8,5 x 11 и 11 x 17)

Приложение 2, — Городской дизайн (c) Отчет о западной лужайке (62 МБ) (размер шрифта смешанный, 8,5 x 11 и 11 x 17)

Приложение 3 — Бенчмаркинг (a) Подробные аннотации состояний и (b) Сравнительный анализ состояний (4,4 МБ) (размер печати смешанный, 8.5 x 11 и 11 x 17)

Документ Приложения 4 и главы, посвященные оценке отдельных объектов, имеют размер шрифта 8,5 x 11

Приложение 4 — Оценка объектов — Содержание (238 кб)

Дополнительное здание Капитолия (1375 Шерман, Денвер) (4,8 МБ)

Centennial Building (1313 Шерман, Денвер) (3,6 МБ)

1570 Грант Билдинг (1570 Грант, Денвер) (4,2 МБ)

Северный кампус Западное здание, (1001 E.62nd, Denver) (4,5 МБ)

1881 Пирс Билдинг (1881 Пирс, Лейквуд) (5,3 МБ)

State Office Building (201 E. Colfax, Denver) (5,1 МБ)

Здание законодательной службы (200 E. 14th, Денвер) (4,8 МБ)

Здание социальных служб (1575 Шерман, Денвер) (3,5 МБ)

Здание государственной службы (1525 Шерман, Денвер) (3,8 МБ)

Здание электростанции (1341 Шерман, Денвер) (4,1 МБ)

Здание Дейла Тули (690 Киплинг, Лейквуд) (4.1 МБ)

Здание Киплинга 700 (700 Киплинг, Лейквуд) (3,4 МБ)

Капитолий штата (200 Э. Колфакс, Денвер) (6,4 МБ)

North Campus North Building (6321 Н. Даунинг, Денвер) (3,9 МБ)

North Campus East Building (6221 Н. Даунинг, Денвер) (3,1 МБ)

Executive Residence (400 E. 8th, Денвер) (5,0 МБ)

Здание государственных служб Гранд-Джанкшн (222 S. 6th, Grand Junction) (3,5 МБ)

Camp George West Site (15000 S. Golden, Pleasant View) (2.9 МБ)

.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт