Таблица про – Таблица производных. Таблица производных полная для студентов и правила дифференцирования. Таблица производных функций. Табличные производные. Формулы производных.

Таблица производных — Википедия

Материал из Википедии — свободной энциклопедии

Вычисление производной — важнейшая операция в дифференциальном исчислении. Эта статья содержит список формул для нахождения производных от некоторых функций.

В этих формулах f{\displaystyle f} и g{\displaystyle g} — произвольные дифференцируемые функции вещественной переменной, а c{\displaystyle c} — вещественная константа. Этих формул достаточно для дифференцирования любой элементарной функции.

• ddxc=0{\displaystyle {d \over dx}c=0}

• ddxx=1{\displaystyle {d \over dx}x=1}

• ddxcx=c{\displaystyle {d \over dx}cx=c}

Вывод

(cx)′=cx′=c{\displaystyle (cx)’=cx’=c}

• ddxxc=cxc−1,{\displaystyle {d \over dx}x^{c}=cx^{c-1},}        когда xc{\displaystyle x^{c}} и cxc−1{\displaystyle cx^{c-1}} определены, c≠0{\displaystyle c\neq 0}

• ddx|x|=x|x|=sgn⁡x,x≠0{\displaystyle {d \over dx}|x|={x \over |x|}=\operatorname {sgn} x,\qquad x\neq 0}

Вывод

Так как |x|=x2{\displaystyle |x|={\sqrt {x^{2}}}}, то пусть g(x)=x2,h(x)=x{\displaystyle g(x)=x^{2},\quad h(x)={\sqrt {x}}} и f(x)=h(g(x))=x2=|x|{\displaystyle f(x)=h(g(x))={\sqrt {x^{2}}}=|x|}

Тогда f′(x)=h′(g(x))⋅g′(x)=12×2⋅2x=xx2=x|x|{\displaystyle f'(x)=h'(g(x))\cdot g'(x)={\frac {1}{2{\sqrt {x^{2}}}}}\cdot 2x={\frac {x}{\sqrt {x^{2}}}}={\frac {x}{|x|}}}

• ddx(1x)=ddx(x−1)=−x−2=−1×2{\displaystyle {d \over dx}\left({1 \over x}\right)={d \over dx}\left(x^{-1}\right)=-x^{-2}=-{1 \over x^{2}}}

• ddx(1xc)=ddx(x−c)=−cxc+1{\displaystyle {d \over dx}\left({1 \over x^{c}}\right)={d \over dx}\left(x^{-c}\right)=-{c \over x^{c+1}}}

• ddxx=ddxx12=12x−12=12x,x>0{\displaystyle {d \over dx}{\sqrt {x}}={d \over dx}x^{1 \over 2}={1 \over 2}x^{-{1 \over 2}}={1 \over 2{\sqrt {x}}},\qquad x>0}

• ddxxn=ddxx1n=1nx1−nn=1n⋅xn−1n{\displaystyle {d \over dx}{\sqrt[{n}]{x}}={d \over dx}x^{1 \over n}={1 \over n}x^{1-n \over n}={\frac {1}{n\cdot {\sqrt[{n}]{x^{n-1}}}}}}

• ddxcx=cxln⁡c,c>0{\displaystyle {d \over dx}c^{x}={c^{x}\ln c},\qquad c>0}

Вывод

ddxcx=ddxexln⁡c=exln⁡cln⁡c=cxln⁡c{\displaystyle {d \over dx}c^{x}={d \over dx}e^{x\ln c}=e^{x\ln c}\ln c=c^{x}\ln c}

• ddxex=ex{\displaystyle {d \over dx}e^{x}=e^{x}}

• ddxef(x)=f′(x)ef(x){\displaystyle {d \over dx}e^{f(x)}=f'(x)e^{f(x)}}

• ddxln⁡x=1x{\displaystyle {d \over dx}\ln x={1 \over x}}
• ddxloga⁡x=loga⁡ex=1xln⁡a{\displaystyle {d \over dx}\log _{a}x={\frac {\log _{a}e}{x}}={\frac {1}{x\ln a}}}

Вывод

loga(x+h)=logax+(logax)′h+o(h){\displaystyle log_{a}(x+h)=log_{a}x+(log_{a}x)’h+o(h)}

loga(x+h)−logax=(logax)′h+o(h){\displaystyle log_{a}(x+h)-log_{a}x=(log_{a}x)’h+o(h)}

loga(1+hx)=(logax)′h+o(h){\displaystyle log_{a}(1+{\frac {h}{x}})=(log_{a}x)’h+o(h)}

logaehx=(logax)′h+o(h){\displaystyle log_{a}e{\frac {h}{x}}=(log_{a}x)’h+o(h)}

• ddxloga⁡f(x)=ddxln⁡f(x)ln⁡(a)=f′(x)f(x)ln⁡(a).{\displaystyle {\frac {d}{dx}}\log _{a}f(x)={\frac {d}{dx}}{\frac {\ln f(x)}{\ln(a)}}={\frac {f'(x)}{f(x)\ln(a)}}.}

• ddxsin⁡x=cos⁡x{\displaystyle {d \over dx}\sin x=\cos x}

• ddxcos⁡x=−sin⁡x{\displaystyle {d \over dx}\cos x=-\sin x}

• ddxtgx=sec2⁡x=1cos2⁡x=tg2⁡x+1{\displaystyle {d \over dx}\,\operatorname {tg} \,x=\sec ^{2}x={1 \over \cos ^{2}x}=\operatorname {tg} ^{2}x+1}

• ddxctgx=−cosec2x=−1sin2⁡x{\displaystyle {d \over dx}\,\operatorname {ctg} \,x=-\,\operatorname {cosec} ^{2}\,x={-1 \over \sin ^{2}x}}

• ddxsec⁡x=tgxsec⁡x{\displaystyle {d \over dx}\sec x=\,\operatorname {tg} \,x\sec x}

• ddxcosecx=−ctgxcosecx{\displaystyle {d \over dx}\,\operatorname {cosec} \,x=-\,\operatorname {ctg} \,x\,\operatorname {cosec} \,x}

• ddxarcsin⁡x=11−x2{\displaystyle {d \over dx}\arcsin x={1 \over {\sqrt {1-x^{2}}}}}

• ddxarccos⁡x=−11−x2{\displaystyle {d \over dx}\arccos x={-1 \over {\sqrt {1-x^{2}}}}}

• ddxarctgx=11+x2{\displaystyle {d \over dx}\,\operatorname {arctg} \,x={1 \over 1+x^{2}}}

• ddxarcctgx=−11+x2{\displaystyle {d \over dx}\,\operatorname {arcctg} \,x={-1 \over 1+x^{2}}}

• ddxarcsec⁡x=1|x|x2−1{\displaystyle {d \over dx}\operatorname {arcsec} x={1 \over |x|{\sqrt {x^{2}-1}}}}

• ddxarccosecx=−1|x|x2−1{\displaystyle {d \over dx}\,\operatorname {arccosec} \,x={-1 \over |x|{\sqrt {x^{2}-1}}}}

ddxshx=chx{\displaystyle {d \over dx}\,\operatorname {sh} \,x=\,\operatorname {ch} \,x}

ddxchx=shx{\displaystyle {d \over dx}\,\operatorname {ch} \,x=\,\operatorname {sh} \,x}

ddxthx=sech3x{\displaystyle {d \over dx}\,\operatorname {th} \,x=\,\operatorname {sech} ^{2}\,x}

ddxsechx=−th⁡xsechx{\displaystyle {d \over dx}\,\operatorname {sech} \,x=-\operatorname {th} x\,\operatorname {sech} \,x}

ddxcthx=−csch3x{\displaystyle {d \over dx}\,\operatorname {cth} \,x=-\,\operatorname {csch} ^{2}\,x}

ddxcschx=−cthxcschx{\displaystyle {d \over dx}\,\operatorname {csch} \,x=-\,\operatorname {cth} \,x\,\operatorname {csch} \,x}

ddxarshx=1×2+1{\displaystyle {d \over dx}\,\operatorname {arsh} \,x={1 \over {\sqrt {x^{2}+1}}}}

ddxarchx=1×2−1{\displaystyle {d \over dx}\,\operatorname {arch} \,x={1 \over {\sqrt {x^{2}-1}}}}

ddxarthx=11−x2{\displaystyle {d \over dx}\,\operatorname {arth} \,x={1 \over 1-x^{2}}}, при |x|<1{\displaystyle |x|<1}

ddxarsechx=−1×1−x2{\displaystyle {d \over dx}\,\operatorname {arsech} \,x={-1 \over x{\sqrt {1-x^{2}}}}}

ddxarcthx=11−x2{\displaystyle {d \over dx}\,\operatorname {arcth} \,x={1 \over 1-x^{2}}}, при |x|>1{\displaystyle |x|>1}

ddxarcschx=−1|x|1+x2{\displaystyle {d \over dx}\,\operatorname {arcsch} \,x={-1 \over |x|{\sqrt {1+x^{2}}}}}

Правила дифференцирования общих функций[править | править код]

(cf)′=cf′{\displaystyle \left({cf}\right)’=cf’}

(f+g)′=f′+g′{\displaystyle \left({f+g}\right)’=f’+g’}

(f−g)′=f′−g′{\displaystyle \left({f-g}\right)’=f’-g’}

(fg)′=f′g+fg′{\displaystyle \left({fg}\right)’=f’g+fg’} (частный случай формулы Лейбница)

(fg)′=f′g−fg′g2,g≠0{\displaystyle \left({f \over g}\right)’={f’g-fg’ \over g^{2}},\qquad g\neq 0}

(fg)′=(egln⁡f)′=fg(f′gf+g′ln⁡f),f>0{\displaystyle (f^{g})’=\left(e^{g\ln f}\right)’=f^{g}\left(f'{g \over f}+g’\ln f\right),\qquad f>0}

(f(g(x)))′=f′(g(x))⋅g′(x){\displaystyle (f(g(x)))’=f'(g(x))\cdot g'(x)} — Правило дифференцирования сложной функции

f′=(ln⁡f)′f,f>0{\displaystyle f’=(\ln f)’f,\qquad f>0}

(fc)′=c(fc−1)f′{\displaystyle (f^{c})’=c\left(f^{c-1}\right)f’}

Таблица умножения и игра, чтобы быстро выучить

С лучшей бесплатной игрой таблица умножения учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Таблица умножения – таблица, где строки и столбцы озаглавлены множителями (1, 2, 3, 4, 5…), а ячейки таблицы содержат их произведение. Применяется таблица для обучения умножению. Здесь есть игра и картинка для печати. Для скачивания игры с таблицей на компьютер, сохраните страницу (Ctrl+S). Также посмотрите таблицу деления.

Смотрите ниже шпаргалки в полной форме.

Распечатать таблицу умножения

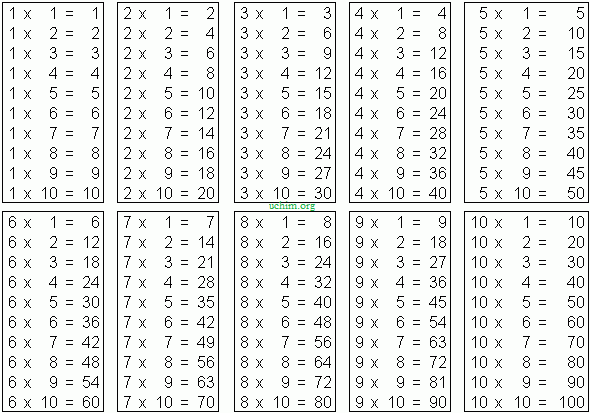
Умножение прямо на сайте (онлайн)

*

https://uchim.org/matematika/tablica-umnozheniya — uchim.org

Таблица умножения (числа от 1 до 20)

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

Нужно распечатать таблицу умножения? Просто нажмите на ссылку печать таблицы умножения. Либо скопируйте картинку (первая таблица) в Ворд (Microsoft Office Word) и распечатайте с помощью сочетания клавиш Ctrl+P. Смотрите также таблицу квадратов.

Всё для учебы » Математика в школе » Таблица умножения и игра, чтобы быстро выучить

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

Таблица производных. Таблица производных полная для студентов и правила дифференцирования. Таблица производных функций. Табличные производные. Формулы производных.

Если x — независимая переменная, то:
Производная степенной функции	Производная степенной функции
—
Производная экспоненциальной функции	Производная экспоненты
Производная сложной экспоненциальной функции	Производная экспоненциальной функции
—

Игры Таблица Умножения — играть онлайн бесплатно

Онлайн игры «Таблица умножения» — серия развивалок, которые бесплатно знакомят малышей с основой основ арифметики. С ними просто выучиться считать, умножать, вычитать и складывать. По сути, это адаптированные для компьютеров и смартфонов тренажеры математики. Чем дольше играть, тем больше чисел и примеров можно выучить.

Таблица умножения, она же — таблица Пифагора, появилась 4000 лет назад. И вот уже пятое тысячелетие подряд дети всего мира запоминают ее одним и тем же способом – учат на память. Только в зазубренном до автоматизма виде этот материал имеет смысл.

И тут малышей подстерегает сложность. Кто учился в школе, хорошо помнит, насколько зубрить – нудное занятие. Как с первых секунд начинает хотеться спать, трудно сосредоточиться, все вокруг бесит, а окружающих ненавидишь (особенно, учительницу математики).

Родители (а таблицу умножения большинство учит в начальных классах под присмотром родителей) видя, что ребенок отвлекся, начинают сердиться, дети в ответ капризничают и разорвать этот порочный круг бывает непросто. Онлайн игры «Таблица умножения» сделают это за вас. Многочисленные исследования показали, что игровая форма обучения – самый эффективный способ усвоить новый материал. Причем, не только для детей, но и для взрослых. Для малышей же, чей мозг не способен сосредотачиваться на чем-то дольше 30-40 минут, они — просто находка. Веселые сюжеты, герои, яркая графика – ни одного шанса заскучать.

Хотя по факту, онлайн игры про таблицу умножения – та же зубрежка, но приведенная в единственно удобоваримую для восприятия форму.

Как играть

Начинать советуем с игрушек, посвященных умножению одного или двух чисел. Самые простые примеры с двойками и тройками. Их, если вдруг ребенок не знает ответ, может быстро решить в уме. Процесс запоминания состоит из двух этапов:

• повторения таблички в учебнике или тетрадке,
• закрепления знаний в игре.

Во время зубрежки важно не дать малышу заскучать. Не стоит повторять примеры больше 5-10 минут. Достаточно один раз разобрать табличку, скажем, умножения на 3, повторить раз-другой, и поскорее переходить к играм. И тут взрослых, помогающих ребенку с арифметикой, ждет удивительный феномен.

Почему-то, когда ответа на 3*2 требует мама или учительница в школе, ничего решать не хочется. А когда мультяшный зайка трижды сходил в такой же мультяшный магазин и каждый раз покупал там по две морковки, невозможно удержаться, что бы не помочь ему их пересчитать. Чудеса, правда?

Таблица умножения — Википедия

Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.

Старейшая известная таблица умножения обнаружена в Древнем Вавилоне и имеет возраст примерно 4000 лет. Она основана на шестидесятеричной системе счисления^[1]. Старейшая десятеричная таблица умножения найдена в Древнем Китае и датируется 305 годом до н. э.^[1]

Иногда изобретение таблицы умножения приписывают Пифагору, в честь которого она названа в различных языках, включая французский, итальянский и русский^[2].

В 493 году Викторий Аквитанский создал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50

[3].

В России первая таблица умножения была издана в 1682 году в первой печатной математической книге на русском языке, называвшейся «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи…» и содержавшей таблицу умножения пар чисел от 1×1 до 100×100, записанных славянскими цифрами^[4]. По экземпляру этой книги хранится, например, в РГБ^[5] и в Научной библиотеке МГУ^[6].

Джон Лесли в книге The Philosophy of Arithmetic (1820)^[7] опубликовал таблицу умножения чисел до 99, позволявшую перемножать цифры парами. Он же рекомендовал ученикам заучивать таблицу умножения до 25.

В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.

В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).

В Советском Союзе таблицу умножения обычно «задавали на лето» после 1-го класса, а закрепляли на занятиях во 2-м классе (в возрасте 8 лет). В российских школах чаще всего проходят во 2-м классе. По стандартам английского школьного образования таблица умножения должна быть выучена к возрасту 11 лет (планируется ужесточение требования до 9 лет).^[8]

Таблица умножения в десятичной системе

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как найти результат по таблице умножения[править | править код]

Чтобы узнать результат произведения 4×8 по таблице умножения, нужно найти четвёрку в левом столбце и восьмёрку в верхней строке, провести от 4 горизонтальную линию и от 8 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 32).

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50

Помимо широко известного применения классической таблицы умножения для выработки практических навыков умножения натуральных чисел, её можно использовать в некоторых математических доказательствах, например, при выводе формулы суммы кубов натуральных чисел или получении подобного выражения для суммы квадратов^[9].

Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.

Таблица Кэли — в общей алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.

В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.

Модулярная арифметика[править | править код]

Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:

Таблица умножения в кольце вычетов по модулю 8

×	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	0	2	4	6
3	0	3	6	1	4	7	2	5
4	0	4	0	4	0	4	0	4
5	0	5	2	7	4	1	6	3
6	0	6	4	2	0	6	4	2
7	0	7	6	5	4	3	2	1

Таблица умножения в поле вычетов по модулю 5

×	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4	1	3
3	0	3	1	4	2
4	0	4	3	2	1

1. ↑ ^{1 2} Jane Qiu. Ancient times table hidden in Chinese bamboo strips (англ.) // Nature : journal. — 2014. — 7 January. — DOI:10.1038/nature.2014.14482.
2. ↑ Например, в Farrar, John. An Elementary Treatise on Arithmetic (англ.).
3. ↑ Maher, David W.; Makowski, John F. Literary evidence for Roman arithmetic with fractions (англ.) // Classical Philology. — 2001. — No. 4 (96). — P. 383.
4. ↑ Депман И. А. История арифметики. Пособие для учителей. — М.: Государственное учебно-педагогическое издательство Министерства Просвещения РСФСР, 1959. — С. 196—198. — 28 000 экз.
5. ↑ Считание удобное : Таблица умножения — карточка электронного каталога РГБ
6. ↑ Считание удобное : Таблица умножения — карточка каталога Научной библиотеки МГУ
7. ↑ Leslie, John. The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand (англ.). — Edinburgh: Abernethy & Walker, 1820.
8. ↑ Children must learn times tables by age nine… // Daily Mail, 17.12.2011
9. ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—72.

Электронная таблица — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 января 2019; проверки требуют 8 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 января 2019; проверки требуют 8 правок.

Электронная таблица^[1] — компьютерная программа, позволяющая проводить вычисления с данными, представленными в виде двумерных массивов, имитирующих бумажные таблицы^[2]. Некоторые программы организуют данные в «листы», предлагая, таким образом, третье измерение.

Электронные таблицы (ЭТ) представляют собой удобный инструмент для автоматизации вычислений. Многие расчёты, в частности в области бухгалтерского учёта, выполняются в табличной форме: балансы, расчётные ведомости, сметы расходов и т. п. Кроме того, решение численными методами целого ряда математических задач удобно выполнять именно в табличной форме. Использование математических формул в электронных таблицах позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Решения многих вычислительных задач, которые раньше можно было осуществить только с помощью программирования, стало возможным реализовать через математическое моделирование в электронной таблице.

Идею электронных таблиц впервые сформулировал американский учёный австрийского происхождения Ричард Маттисич (нем. Richard Mattesich), опубликовав в 1961 году исследование под названием «Budgeting Models and System Simulation»^[3]. Концепцию дополнили в 1970 году Рене Пардо (англ. Rene Pardo) и Реми Ландау (англ. Remy Landau), подавшие заявку на соответствующий патент (U.S. Patent 4 398 249). Патентное ведомство отклонило заявку, но авторы через суд добились этого решения.

Общепризнанным родоначальником электронных таблиц как отдельного класса ПО является Дэн Бриклин, который совместно с Бобом Фрэнкстоном разработал программу VisiCalc в 1979 году. Эта электронная таблица для компьютера Apple II стала очень популярной, превратив персональный компьютер из игрушки для технофилов в массовый инструмент для бизнеса.

Впоследствии на рынке появились многочисленные продукты этого класса — SuperCalc, Microsoft MultiPlan (англ.)русск., Quattro Pro, Lotus 1-2-3, Microsoft Excel, OpenOffice.org Calc, таблицы AppleWorks (англ.)русск. и gnumeric, минималистический Spread32.

Существуют электронные таблицы для мобильных телефонов и карманных персональных компьютеров, в частности SpreadCE.

Также в своё время были достаточно известны программы: Quattro Pro, SuperCalc и VisiCalc.

Таблица Сивцева — Википедия

Материал из Википедии — свободной энциклопедии

Эта статья или раздел описывает ситуацию применительно лишь к одному региону (Россия), возможно, нарушая при этом правило о взвешенности изложения. Вы можете помочь Википедии, добавив информацию для других стран и регионов.

Таблица Сивцева — наиболее распространённая на территории бывшего СССР таблица, применяемая для проверки остроты зрения. Таблица названа в честь Дмитрия Александровича Сивцева, советского офтальмолога (1875—1940), который разработал её в 1925 году^[1].

В этой таблице содержатся строки печатных букв (всего 12 строк), размер букв уменьшается от строки к строке в направлении сверху вниз. Слева каждой строки указано расстояние D{\displaystyle D} (в метрах), с которого их должен видеть человек с нормальным зрением (50,0 метров для верхнего ряда; 2,5 метра — для нижнего). Справа каждой строки указана величина V{\displaystyle V} (в условных единицах) — это острота зрения при чтении букв с расстояния 5 метров (0,1 если глаз видит только верхний ряд; 2,0 — если виден нижний ряд). Нормальное зрение (1,0) — когда человек видит каждым глазом с расстояния 5 метров десятую строку.

Чтобы вычислить размер букв на определённой строке (с погрешностью примерно 1 миллиметр), надо 7 миллиметров разделить на величину V (значение на этой строке). Так, размер букв на верхней строке (V=0,1{\displaystyle V=0,1}) будет 70 миллиметров; на нижней (V=2,0{\displaystyle V=2,0}) — буквы размером 3,5 миллиметра.

При исследовании остроты зрения с другого расстояния (меньше 0,1 — если человек с 5 метров не распознаёт буквы верхнего ряда), проверяемого приближают к таблице и через каждые 0,5 метра спрашивают, пока он не назовёт правильно буквы верхнего ряда. Величина рассчитывается по формуле:

V=dD{\displaystyle V={\frac {d}{D}}}, где

• V{\displaystyle V} — острота зрения;
• d{\displaystyle d} — расстояние, с которого проводится исследование;
• D{\displaystyle D} — расстояние, на котором нормальный глаз видит данный ряд.

Но лучше для определения остроты зрения меньше 0,1 с 5 метров использовать оптотипы Поляка.

Офтальмологи, как правило, используют эту таблицу совместно с таблицей Головина.

• В таблице используются только 7 букв русского алфавита: Ш, Б, М, Н, К, Ы, И
• Условно принято считать, что глаз с остротой зрения 1,0 способен увидеть раздельно две далёкие точки, если угловое расстояние между ними равно одной угловой минуте (¹⁄₆₀ градуса). При расстоянии 5 метров это соответствует 1,45 миллиметра — таким должно быть расстояние между ближайшими палочками буквы «Ш» в десятой строке на проверочной таблице.
• При эмметропии точка ясного видения находится как бы в бесконечности. Для человеческого глаза бесконечность начинается на расстоянии 5 метров: при расположении предмета не ближе 5 метров на сетчатке глаза с эмметропией собираются параллельные лучи. Именно поэтому проверку остроты зрения осуществляют с такого расстояния.