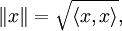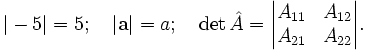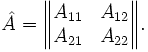{ — Левая фигурная скобка (U+007B)
Начертание символа «Левая фигурная скобка» в разных шрифтах
Описание символа
Левая фигурная скобка. Основная латиница.
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | 7B | 123 | 123 | 01111011 |
| UTF-16BE | 00 7B | 0 123 | 123 | 00000000 01111011 |
| UTF-16LE | 7B 00 | 123 0 | 31488 | 01111011 00000000 |
| UTF-32BE | 00 00 00 7B | 0 0 0 123 | 123 | 00000000 00000000 00000000 01111011 |
| UTF-32LE | 7B 00 00 00 | 123 0 0 0 | 2063597568 | 01111011 00000000 00000000 00000000 |
Угловые скобки Википедия
Запрос «:)» и другие, начинающиеся с двоеточия, перенаправляются сюда; об их значении см. Смайлик.| Скобки | |
|---|---|
| () | |
Изображение
| |
| (: left parenthesis ): right parenthesis | |
| Юни | (: U+0028 ): U+0029 |
| HTML- | (: ): |
| UTF-16 | (: 0x28 ): 0x29 |
| (: %28 ): %29 | |
Ско́бки — парные знаки, используемые в различных областях.
Различают:
- круглые ( ) скобки;
- квадратные [ ] скобки;
- фигурные { } скобки;
- угловые ⟨ ⟩ скобки (или < > в ASCII-текстах).
Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.).
Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
Используются в математике, физике, химии и других науках для установки приоритета выполнения операции в формулах.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.
} — Правая фигурная скобка (U+007D)
Начертание символа «Правая фигурная скобка» в разных шрифтах
Описание символа
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | 7D | 125 | 125 | 01111101 |
| UTF-16BE | 00 7D | 0 125 | 125 | 00000000 01111101 |
| UTF-16LE | 7D 00 | 125 0 | 32000 | 01111101 00000000 |
| UTF-32BE | 00 00 00 7D | 0 0 0 125 | 125 | 00000000 00000000 00000000 01111101 |
| UTF-32LE | 7D 00 00 00 | 125 0 0 0 | 2097152000 | 01111101 00000000 00000000 00000000 |
Скобки | Virtual Laboratory Wiki
- Сюда перенаправляются запросы 🙂 и некоторые другие, начинающиеся с двоеточия. О них см. статью смайлик.
Ско́бки — па́рные знаки, используемые в различных областях.
Различают:
- круглые () скобки;
- квадратные [ ] скобки;
- фигурные { } скобки;
- угловые $ \langle\; \rangle $ скобки (или < > в ASCII-текстах).
Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.).
Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
В математике, физике, химии и др. используются при написании формул.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.
В системе вёрстки TEΧ есть возможность автоматически подстраивать размер скобок под вложенный в него текст: это делается с помощью команд \left и \right. Следует заметить, что во избежание синтаксических ошибок эти две команды всегда должны соответствовать друг другу, однако виды скобок в них — не обязательно. Это делает возможным конструкцию вида «\left\{ a \\ a \right.» для записи систем уравнений.
Круглые скобки
( )
Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение $ (A \lor B) \land C $ означает, что сначала выполняется логическое сложение $ (\lor ), $ а затем — логическое умножение $ (\land ). $ Наряду с квадратными скобками используются также для записи компонент векторов:
- $ \mathbf{a} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $
и матриц:
- $ \hat{A} = \begin{pmatrix} x & y \\ z & v \end{pmatrix}; $
для записи биномиальных коэффициентов:
- $ C^k_n = {n \choose k}. $
Круглые скобки в математике используются также для выделения аргументов функции: $ w = f(x)+g(y,z)\,, $ для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
- $ \mathbf{c}=(\mathbf{a},\mathbf{b}) = (\mathbf{a} \cdot \mathbf{b}) = \mathbf{a} \cdot \mathbf{b} $
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
- $ \mathbf{d}=(\mathbf{a},\mathbf{b},\mathbf{c}). $
При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1<A<3. Это называется (открытый) интервал.
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки
[ ]
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек».
Квадратными скобками в математике могут обозначаться:
- Операция взятия целой части числа.
- Для задания приоритета операций (аналогично круглым) в качестве скобок «второго уровня» — так легче различать вложенность скобок, например: [(2+3)·4]².
- Векторное произведение векторов: c=[a,b]=[a×b]=a × b.
- Закрытые сегменты; запись [1;3] означает, что в множество включены числа $ 1 \leq x \leq 3 $. В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y).
- Коммутатор $ [A,B] \equiv [A,B]_- \equiv AB-BA\! $ и антикоммутатор $ [A,B]_+ \equiv AB+BA\,, $ хотя для последнего иногда используют фигурные скобки без нижнего индекса.
- Одинарная квадратная скобка объединяет совокупность уравнений или неравенств (чтобы совокупность выполнялась, достаточно, чтобы выполнялось любое из уравнений).
В химии квадратными скобками обозначают комплексные анионы и катионы, например: Na2[Fe(NO)(CN)5], [Ag(NH3)2]+. Также, по номенклатуре IUPAC в квадратные скобки залючается количество атомов в мостиках между двумя атомами в названии органических полициклических соединений, например: бицикло[2,2,2]октан.
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива.
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки
{ }
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: $ \{f, g\} \,. $ Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
В вики-разметке двойные фигурные скобки применяются для шаблонов.
В программировании фигурные скобки являются или операторными (Си, Java, Perl и PHP), или комментарием (Паскаль), могут также служить для образования списка (в Mathematica).ь
Угловые скобки
$ \langle\;\rangle $
В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:
- $ \|x\| = \sqrt{\langle x,x\rangle}, $
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как $ |\psi\rangle $ (кет-вектор) и $ \langle \psi | $ (бра-вектор), их скалярное произведение как $ \langle \psi_k |\psi_l\rangle, $ матричный элемент оператора А в определённом базисе как $ \langle k |A| l\rangle. $
Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, $ \langle f(t)\rangle $ — среднее значение по времени от величины f.
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — $ \langle … \rangle $.
Типографика
В ASCII-текстах (в том числе HTML / XML и программировании) для записи угловых скобок используют схожие по написанию парные знаки арифметических отношений неравенства «<» и «>».
В типографике же угловые скобки $ \mathcal {hi} $ являются самостоятельными символами. От «<» и «>» их можно отличить по бо́льшему углу между сторонами — $ \langle\rangle~u<> $.
В ТеХе для записи угловых скобок используются команды «\langle» и «\rangle».
В стандартной пунктуации китайского, японского и корейского языков используются специальные символы — шевроны (англ. chevron), схожие по написанию с угловыми скобками — для горизонтальной 〈
Скобки в математике: их виды и предназначение
В данной статье рассказывается о скобках в математике и рассматриваются виды и применения, термины и методы использования при решении или для описания материала. В заключение будут решены подобные примеры с подробными комментариями.
Основные виды скобок, обозначения, терминология
Для решения заданий в математике используются три вида скобок: ( ), [ ], { }. Реже встречаются скобки такого вида ] и [, называемые обратными, или < и >, то есть в виде уголка. Их применение всегда парное, то есть имеется открывающаяся и закрывающаяся скобка в любом выражении, тогда оно имеет смысл . скобки позволяют разграничить и определить последовательность действий.
Фигурная непарная скобка типа { встречается при решении систем уравнений, что обозначает пересечение заданных множеств, а [ скобка используется при их объединении. Далее рассмотрим их применение.
Скобки для указания порядка выполнения действий
Основное предназначение скобок – указание порядка выполняемых действий. Тогда выражение может иметь одну или несколько пар круглых скобок. По правилу всегда выполняется первым действие в скобках, после чего умножение и деление, а позже сложение и вычитание.
Пример 1Рассмотрим на примере заданное выражение. Если дан пример вида 5+3-2, тогда очевидно, что действия выполняются последовательно. Когда это же выражение записывается со скобками, тогда их последовательность меняется. То есть при (5+3)-2 первое действие выполняется в скобках. В данном случае изменений не будет. Если выражение будет записано в виде 5+(3-2), тогда в начале производятся вычисления в скобках, после чего сложение с числом 5. На исходное значение в этом случае оно не повлияет.
Пример 2Рассмотрим пример, который покажет, как при изменении положения скобок может измениться результат. Если дано выражение 5+2·4, видно, что вначале выполняется умножение, после чего сложение. Когда выражение будет иметь вид (5+2)·4, то вначале выполнится действие в скобках, после чего произведется умножение. Результаты выражений будут отличаться.
Выражения могут содержать несколько пар скобок, тогда выполнения действий начинаются с первой. В вы
⏝ — Круглая скобка вниз (U+23DD)
Начертание символа «Круглая скобка вниз» в разных шрифтах
⏝Ваш браузер
Описание символа
Круглая скобка вниз. Разнообразные технические символы.
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8F 9D | 226 143 157 | 14847901 | 11100010 10001111 10011101 |
| UTF-16BE | 23 DD | 35 221 | 9181 | 00100011 11011101 |
| UTF-16LE | DD 23 | 221 35 | 56611 | 11011101 00100011 |
| UTF-32BE | 0 0 35 221 | 9181 | 00000000 00000000 00100011 11011101 | |
| UTF-32LE | DD 23 00 00 | 221 35 0 0 | 3710058496 | 11011101 00100011 00000000 00000000 |
Угловые скобки — это… Что такое Угловые скобки?
угловые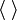 скобки (или < > в
скобки (или < > вИспользуются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.
В математике, физике, химии и др. используются при написании формул.
Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.
В системе вёрстки \left и \right. Следует заметить, что во избежание синтаксических ошибок эти две команды всегда должны соответствовать друг другу, однако виды скобок в них — не обязательно. Это делает возможным конструкцию вида «\left\{ a \\ a \right.» для записи систем уравнений.
Круглые скобки
( )
Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение 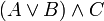 означает, что сначала выполняется логическое сложение
означает, что сначала выполняется логическое сложение 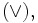 а затем — логическое умножение
а затем — логическое умножение 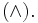 Наряду с квадратными скобками используются также для записи компонент векторов:
Наряду с квадратными скобками используются также для записи компонент векторов:
и матриц:
для записи биномиальных коэффициентов:
Круглые скобки в математике используются также для выделения аргументов функции: 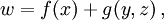 для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1<A<3. Это называется (открытый) интервал.
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки
[ ]
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек».
Квадратными скобками в математике могут обозначаться:
- Операция взятия целой части числа.
- Для задания приоритета операций (аналогично круглым) в качестве скобок «второго уровня» — так легче различать вложенность скобок, например: [(2+3)·4]².
- Векторное произведение векторов: c=[a,b]=[a×b]=a × b.
- Закрытые сегменты; запись [1;3] означает, что в множество включены числа
 . В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y).
. В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y). - Коммутатор
![[A,B] \equiv [A,B]_- \equiv AB-BA\!](//xn--90abhccf7b.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) и антикоммутатор
и антикоммутатор ![[A,B]_+ \equiv AB+BA\,,](//xn--90abhccf7b.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) хотя для последнего иногда используют фигурные скобки без нижнего индекса.
хотя для последнего иногда используют фигурные скобки без нижнего индекса. - Одинарная квадратная скобка объединяет совокупность уравнений или неравенств (чтобы совокупность выполнялась, достаточно, чтобы выполнялось любое из уравнений).
В химии квадратными скобками обозначают комплексные анионы и катионы, например: Na2[Fe(NO)(CN)5], [Ag(NH3)2]+. Также, по номенклатуре IUPAC в квадратные скобки заключается количество атомов в мостиках между двумя атомами в названии органических полициклических соединений, например: бицикло[2,2,2]октан.
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива.
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки
{ }
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: 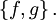 Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
В вики-разметке двойные фигурные скобки применяются для шаблонов.
В программировании фигурные скобки являются или операторными (Си, C++, Perl и комментарием (Паскаль), могут также служить для образования списка (в Сетл).
Угловые скобки
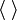
В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как 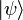 (кет-вектор) и
(кет-вектор) и 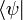 (бра-вектор), их скалярное произведение как
(бра-вектор), их скалярное произведение как 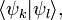 матричный элемент оператора А в определённом базисе как
матричный элемент оператора А в определённом базисе как 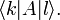
Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, 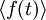 — среднее значение по времени от величины f.
— среднее значение по времени от величины f.
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — 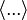 .
.
Типографика
В HTML / программировании) для записи угловых скобок используют схожие по написанию парные знаки арифметических отношений неравенства «<» и «>».
В типографике же угловые скобки 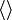 являются самостоятельными символами. От «<» и «>» их можно отличить по бо́льшему углу между сторонами —
являются самостоятельными символами. От «<» и «>» их можно отличить по бо́льшему углу между сторонами — 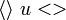 .
.
В ТеХе для записи угловых скобок используются команды «\langle» и «\rangle».
В стандартной пунктуации китайского, японского и корейского языков используются специальные символы — шевроны (англ. chevron), схожие по написанию с угловыми скобками — для горизонтальной 〈 и 〉 или 《 и 》 и традиционной вертикальной печати — ︿ и ﹀ или ︽ и ︾.
ASCII-тексты
В некоторых языках разметки, напр., HTML, XML угловыми скобками выделяют теги.
В вики-разметке также можно использовать HTML-разметку, например комментарии — «<!— Этот абзац надо расширить —>», которые видны только при редактировании статьи.
В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений («<» и «>»). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере:
#include <stdio.h> #include "myheader.h"
файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге исходника программы).
В некоторых текстах, сдвоенные парные «<» и «>» используются для записи кавычек-ёлочек, например — <<цитата>>.
Косые скобки
/…/
Появились на пишущих машинках для экономии клавиш.
В программировании на языке Си косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария:
/* Комментарий в исходном коде на языке Си */
Прямые скобки
|…|
Используются в математике для обозначения модуля числа или вектора, определителя матрицы:
Двойные прямые скобки
||…||
Используются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц:


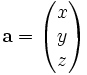
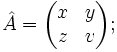
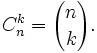
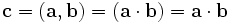
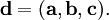
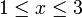 . В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y).
. В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y).![[A,B] \equiv [A,B]_- \equiv AB-BA\!](/800/600/https/dic.academic.ru/pictures/wiki/files/51/306cf34b86f909af1d078266b701e280.png) и антикоммутатор
и антикоммутатор ![[A,B]_+ \equiv AB+BA\,,](/800/600/https/dic.academic.ru/pictures/wiki/files/49/19e407e46b8019750249cdba30f3ff77.png) хотя для последнего иногда используют фигурные скобки без нижнего индекса.
хотя для последнего иногда используют фигурные скобки без нижнего индекса.