Знак менее и более: Больше, меньше, равно — урок. Математика, 1 класс.

5.3. Знаки приоритета \ КонсультантПлюс

5.3. Знаки приоритета

5.3.1. Знаки приоритета применяют для указания очередности проезда перекрестков, пересечений отдельных проезжих частей, а также узких участков дорог.

5.3.2. Знак 2.1 «Главная дорога» устанавливают в начале участка дороги с преимущественным правом проезда нерегулируемых перекрестков.

В населенных пунктах знак устанавливают перед каждым перекрестком на главной дороге. Перед нерегулируемыми перекрестками, на которых главная дорога проходит в прямом направлении, а пересекающая дорога имеет не более четырех полос, допускается устанавливать знак размером 350 х 350 мм.

В населенных пунктах знак допускается не устанавливать на противоположной примыканию стороне перед примыканием второстепенной дороги к главной.

Знак 2.1 с табличкой 8.13 устанавливают перед перекрестками, на которых главная дорога изменяет направление, а также перед перекрестками со сложной планировкой. В населенных пунктах знак 2. 1 с табличкой 8.13 устанавливают перед перекрестком, а вне населенных пунктов — предварительно на расстоянии 150 — 300 м до перекрестка и перед перекрестком (рисунок В.4а).

На пересечениях дорог с несколькими проезжими частями знак устанавливают перед пересечениями проезжих частей, на которых возможно неоднозначное определение главенства дорог.

5.3.3. Знак 2.2 «Конец главной дороги» устанавливают в конце участка дороги, где она утрачивает статус главной.

Если дорога, обозначенная знаком 2.1, оканчивается перед пересечением с дорогой, по которой предоставлено преимущественное право проезда данного перекрестка, то знак 2.2 вне населенных пунктов размещают на одной опоре со знаком 2.4, установленным предварительно с табличкой 8.1.1 или 8.1.2, в населенных пунктах — за 25 м от перекрестка либо со знаком 2.4 или 2.5. Вне населенных пунктов знак 2.2 допускается устанавливать повторно со знаком 2.4 или 2.5, а в населенных пунктах — предварительно с табличкой 8.1.1 на расстоянии 50 — 100 м до основного знака (рисунок В. 4б).

5.3.4. Знаки 2.3.1 «Пересечение с второстепенной дорогой», 2.3.2 — 2.3.7 «Примыкание второстепенной дороги» устанавливают вне населенных пунктов перед всеми перекрестками на дорогах, обозначенных знаком 2.1. Знаки не устанавливают перед перекрестками со сложной планировкой и перед перекрестками, на которых главная дорога изменяет направление. Знаки 2.3.4 — 2.3.7 должны быть установлены, если угол между осями главной и второстепенной дорог составляет менее 60°.

Вне населенных пунктов знаки 2.3.1 — 2.3.7 устанавливают на расстоянии 150 — 300 м, в населенных пунктах — на расстоянии 50 — 100 м до перекрестка. При необходимости допускается устанавливать знаки 2.3.1 — 2.3.7 на ином расстоянии, указываемом в этом случае на табличке 8.1.1.

5.3.5. Допускается не устанавливать знаки 2.1, 2.3.1 — 2.3.7 перед съездами пересечений дорог в разных уровнях, а также перед примыканиями к дороге с твердым покрытием дорог с грунтовым покрытием, перед примыканиями к дороге выездов с прилегающих территорий, если все перечисленные признаки примыкающих дорог могут однозначно распознаваться водителями транспортных средств, следующих по главной дороге в светлое и темное время суток.

5.3.6. Знак 2.4 «Уступите дорогу» применяют для указания того, что водитель должен уступить дорогу транспортным средствам, движущимся по пересекаемой дороге, а при наличии таблички 8.13 — транспортным средствам, движущимся по главной дороге.

Знак устанавливают непосредственно перед выездом на дорогу в начале кривой сопряжения, по которой знаками 2.1 или 2.3.1 — 2.3.7 предоставлено преимущественное право проезда данного перекрестка, а также перед выездами на автомагистраль.

Перед перекрестками со сложной планировкой и перед перекрестками, на которых главная дорога изменяет направление, знак устанавливают с табличкой 8.13.

Знак устанавливают перед выездами с грунтовых дорог на дорогу с твердым покрытием, а также в местах выезда на дорогу с прилегающих территорий, если признаки примыкающих дорог могут неоднозначно распознаваться водителями транспортных средств, выезжающих на главную дорогу в светлое и темное время суток.

Знак 2.4 устанавливают предварительно с табличкой 8. 1.1 на дорогах вне населенных пунктов, за исключением грунтовых дорог, на расстоянии 150 — 300 м до перекрестка, если перед перекрестком установлен знак 2.4, или с табличкой 8.1.2, если перед перекрестком установлен знак 2.5.

При наличии полосы разгона в местах выезда на дорогу с преимущественным правом проезда перекрестков знак устанавливают перед началом этой полосы.

5.3.7. Знак 2.5 «Движение без остановки запрещено» применяют для указания водителю остановиться и уступить дорогу транспортным средствам, движущимся по пересекаемой дороге, а при наличии таблички 8.13 — транспортным средствам, движущимся по главной дороге.

Знак 2.5 устанавливают вместо знака 2.4, если не обеспечена видимость транспортных средств, приближающихся по пересекаемой дороге.

Знак устанавливают перед железнодорожными переездами без дежурного, не оборудованными светофорами, на расстоянии 10 м до ближнего рельса в случаях, если на удалении 50 м от ближайшего рельса расстояние видимости поезда менее значения, указанного в таблице 5.

Знаки и символы математики

Знаки и символы математики

Можно ли заниматься математикой устно или в уме? Или она все-таки невозможна без того, чтобы делать какие-то записи? И если верно последнее, то необходим ли ей для этих целей какой-то особый язык?

Есть основания считать, что да – необходим. Более того, существует точка зрения, что разные языки более или менее подходят для разных областей математики – примерно, как разные мелодии в одних тональностях звучат лучше, чем в других.

Но нам до отдельных областей пока далеко – поэтому поговорим о том математическом символизме, который является общепринятым, но, тем не менее, тоже подчас бывает труден для восприятия неспециалистами.

Поскольку в основе всей стандартной математики лежит теория множеств, то с символов этой теории мы и начнем.

….– символ принадлежности элемента множеству. Поскольку теория множеств не оперирует ничем, кроме множеств, их элементов (которые тоже суть множества) и отношения принадлежности, то символ обозначает единственное отношение, принадлежащее теории.

Квантор всеобщности и знак импликации – это, вообще говоря, не собственно математические символы, а логические. С другой стороны, сама формальная логика является насквозь математической, поэтому данное разделение также является во многом формальным.

Тем не менее, чтобы покончить в первом приближении с логикой, перечислим еще несколько чрезвычайно распространенных логических символов:

V – дизъюнкция, или логическое «или». Логическая связка, при помощи которой из двух суждений А и В образуется сложное суждение A V B, которое ложно, только если оба дизъюнкта ложны.

Здесь надо заметить, что логические связки очень напоминают операции с множествами

Комментарий

Это сходство неслучайно. Дело в том, что суждение Р интуитивно можно себе представлять как МНОЖЕСТВО всех таких элементов (предметов, вещей), в отношении которых суждение Р истинно. Именно поэтому действиям с суждениями и соответствуют действия с множествами.

Еще одним важным математическим символом является обозначение функции

Такая запись означает, что нам дан некоторый закон, по которому каждому элементу множества X сопоставляется ровно один элемент множества Y.

Этот функциональный закон, или правило еще называют отображением, преобразованием и т. п. Мне лично еще нравится английский термин mapping (для которого, к сожалению, нет подходящего слова в русском языке), а им очень хорошо схватывается процесс сопоставления точек местности (объекта Х) с точками на листе бумаги (объекта Y) – откуда, по-видимому, и происходит данный термин (от англ. map – географическая карта).

Хоть понятие функции и не накладывает никаких ограничений на состав множеств, из которых и в которые она действует, все же есть ряд важных числовых множеств, на которых определены многие математические функции:

Обратите внимание, что все эти множества вложены друг в друга, т.  е. являются упорядоченными по включению:

Сталкиваясь с таким многообразием столь непривычных конструкций, именуемых «числами», невольно теряешься и задаешься вопросом: а что вообще считать числом.

Ну вот алгебраический ответ такой: числа – это сущности любой природы, которые можно складывать, вычитать, умножать и делить, оставаясь в пределах того же класса сущностей. Удивительный результат состоит в том, что объектов, сложнее октавов, на множестве которых были бы возможны все четыре арифметические операции, не построить (желающие подробнее вникнуть в результат, о котором идет речь могут почитать про гипотезу Фробениуса и ее доказательствах в 60-х гг. прошлого века).

Принятые обозначения для сумм и произведений:

Если у нас имеется больше двух однотипных слагаемых, то строчку вида

бывает удобно записать с помощью символа суммы Σ:

И то же самое применимо в отношении произведения, которое также кратко записывается с помощью специального символа ∏:

Существуют также символы для сложения и умножения, когда складываются не числа, а, например, целые множества или даже более сложные объекты:

⊕ – прямая сумма. Опять-таки в случае двух множеств – это их так называемое дизъюнктное объединение, когда общие для обоих множеств элементы включаются в прямую сумму только один раз.

Например, прямой суммой множеств A = {1, 2, 3} и B = {2, 3, 4} будет множество

A ⊕ B = {1, 2, 3, 4}

Самое обобщенное определение прямого произведения и прямой суммы любых объектов – множеств, групп, векторных пространств, колец и т. п. – может быть дано на языке теории категорий.

См. Произведение и копроизведение:

Смотреть

Пожалуй, наш список наиболее употребительных математических символов был бы неполным, если бы мы не упомянули в заключение об обозначениях интеграла и производной.

Если у нас имеется некоторая функция f (x), то ее производная обозначается как

а ее интеграл – как

Подробнее об удобствах и основаниях для таких обозначений как производной, так и интеграла читайте в нашем интеллектуальном продукте «Автостопом по математике»:

Наш гид:

Смотреть

«Автостопом по математике»

Написать в чат

Понравилась статья?

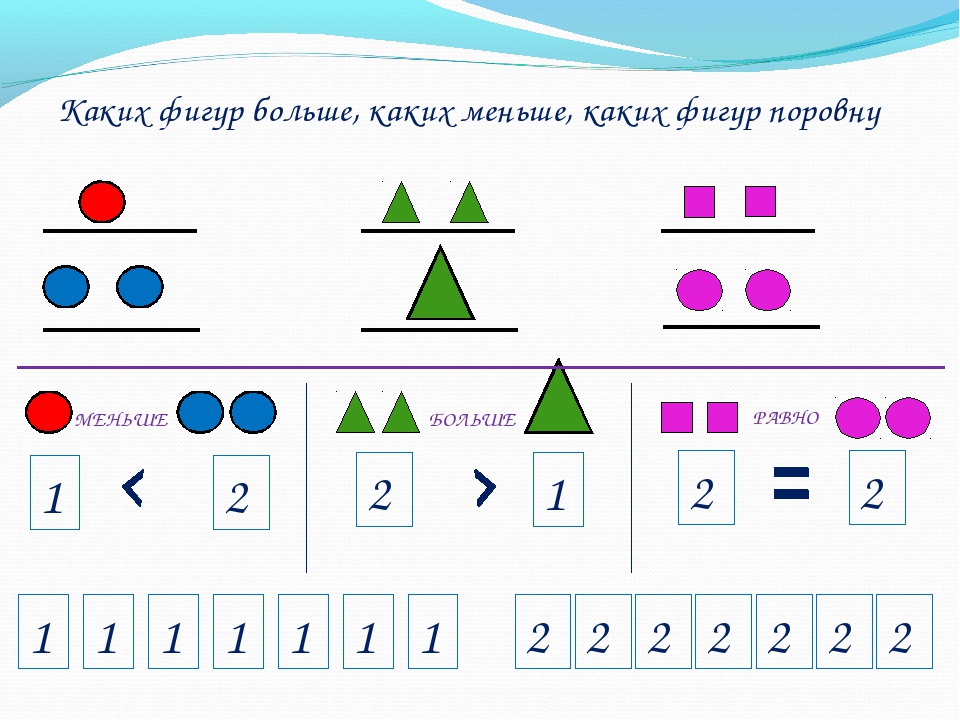
Знаки Больше и Меньше

Опубликовано Математика С Мамой

• 3 больше 1.
• Символ «больше чем» — « > ».
• Пишем «3 > 1», что означает «3 больше 1».
• 6 меньше 8.
• Символ «меньше чем» — «».
• Мы пишем ‘6
• Мы можем помнить, что каждый символ сравнения указывает на меньшее число.
• Открытый конец открыт для большего числа, и мы можем помнить, что крокодил хочет съесть большее число.

«>» означает «больше чем» и « Открытый конец обращен к большему числу, а стрелка указывает на меньшее число.

• 3 меньше 8.
• Мы можем написать ‘3
• Открытый конец символа сравнения обращен к 8, потому что крокодил хочет съесть большее число.
• 7 больше 2,
• Мы можем написать «7 > 2», чтобы стрелка указывала на меньшее число.
• Открытый конец символа сравнения обращен к 7, потому что крокодил хочет съесть большее число.

Рабочие листы и ответы «Больше и меньше»

В этом уроке мы сравниваем числа и пишем символы сравнения между числами, чтобы показать, какое число больше.

Символ «больше чем» — «>».

Символ «меньше чем» — « Способ запомнить, какой знак использовать, заключается в том, что символ будет указывать на меньшее число, как стрелка.

Другой способ запомнить знаки больше или меньше заключается в том, что открытый конец символа будет обращен к большему числу. Мы можем представить символ как открытую пасть крокодила, а затем вспомнить, что крокодил захочет съесть наибольшее количество, чтобы получить больше еды.

В этом уроке мы напишем символы сравнения «больше чем» и «меньше чем», чтобы сравнить два числа.

Мы начнем с нашего первого символа сравнения, равно знаку 9.0013 .

• Знак равенства (=):

Знак равенства означает «то же значение, что и».

Например:

3 + 1 = 4

4 = 4

Это говорит нам о том, что 3 + 1 имеет то же значение, что и четыре.

• Знак «больше» (>):

Знак «больше чем» означает «больше, чем» или «больше, чем».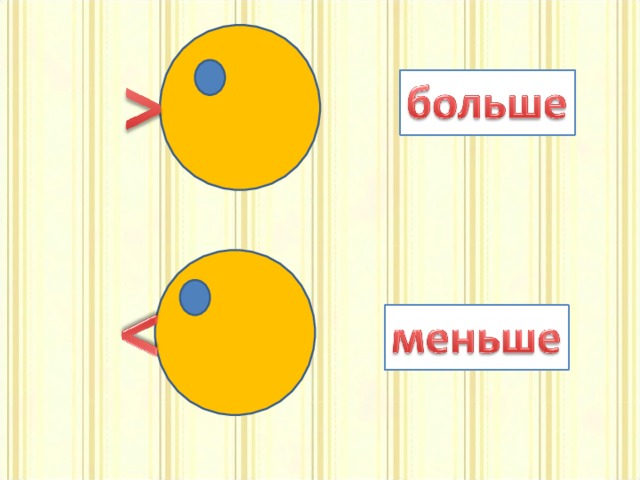

Например:

5 > 4

Мы читаем это как «пять равно 9».0012 больше четыре’.

• Знак меньше (

Знак «меньше» означает «меньше».

Например:

4 Это читается как «четыре на меньше, чем на пять».

Мы будем использовать несколько примеров знаков больше или меньше, чтобы посмотреть, как запомнить направление, в котором рисуются знаки больше и меньше при сравнении двух чисел.

Чтобы определить, больше или меньше число другого числа, мы можем посмотреть на числовую прямую.

Чем дальше мы идем вправо по нашей числовой прямой, тем больше наше число.

Число на больше, чем на другое число, если оно находится правее его на числовой прямой.

Больше Пример:

В приведенном ниже примере мы видим, что 3 больше, чем 1. Итак, мы говорим, что три больше, чем один.

Один из способов запомнить, какой знак ставить между числами, — представить знак сравнения в виде стрелки. Эта стрелка указывает на меньшее число.

Итак, он указывает на 1.

Еще один способ запомнить, какой символ является знаком «больше чем», — представить этот символ в виде крокодила.

Крокодил голоден и хочет съесть большее количество. Итак, его рот открывается в сторону 3.

Меньше Пример:

В приведенном ниже примере мы видим, что 6 меньше числа, чем 8.

Мы знаем это, потому что 6 находится слева от 8 на числовой прямой.

Итак, мы говорим, что шесть меньше восьми.

Мы можем использовать те же два метода, которые мы использовали ранее, чтобы запомнить, какой знак сравнения представляет «меньше чем».

Думайте о символе как о стрелке, которая всегда указывает на меньшее число. Таким образом, он указывает на 6, а не на 8.

Мы также можем думать о знаке «меньше» как о крокодиле, который хочет съесть большее число. Итак, его рот открывается в сторону 8.

При обучении знакам больше и меньше самой большой ошибкой является неправильное написание символов.

К счастью, знаки имеют ту же форму, только в обратном направлении.

Лучший способ запомнить направление — это то, что знак будет указывать на наименьшее число, как стрелка.

Теперь попробуйте наш урок «Сложение в числовой строке: начиная с наибольшего числа », где мы научимся складывать числа, используя числовую строку.

Меньше Знак в математике

Меньше

Отношения между двумя величинами можно описать с помощью условий сравнения. В основном используются три термина сравнения: больше (>), меньше (<) и равно (=).

Больше (>):

Когда одно количество больше другого, мы используем «больше чем».

Например, 5 > 3.

Меньше (<): 

Когда одно количество меньше другого, мы используем «меньше чем».

Например, 8 < 10.

Равно (=): 

Когда две величины одинаковы, мы используем «равно».

Например, 15 = 15.

Родственные игры

Меньше, чем Определение

Это один из терминов, используемых для обозначения взаимосвязи между двумя значениями. В нем говорится, что одно значение меньше или ниже или меньше или меньше другого. Символ «меньше» — это « < », и с помощью этой метрики мы можем сравнивать числа, веса, высоты и значения.

Давайте рассмотрим несколько примеров меньше чем.

Пример 1. В чаше A 4 шарика, а в чаше B 7 шариков. При сравнении двух шариков видно, что в чаше A меньше шариков, чем в чаше B. 

Аналогичным образом можно сравнивать веса.

Пример 2. Рэй покупает 8 фунтов картофеля и 4 фунта помидоров и кладет их в два отдельных мешка. Он передает сумку с зажигалкой своему сыну. Кого он держит в себе?

Ну, для этого важно узнать, какая сумка легче. Есть два мешка, один с картошкой весит 8 фунтов, а другой с помидорами весит 4 фунта. Итак, мешок с помидорами весит меньше, и Рэй передает его своему сыну, а сам несет мешок с картошкой.

Пример 3, у Джона 6 плиток шоколада. У Риты 2 плитки шоколада, а у Сумы 3 плитки шоколада. У Джона шоколадок больше, чем у Риты и Сумы вместе взятых?

Общее количество плиток Риты и Сумы = 2 + 3 = 5 плиток

А у Джона 6 плиток шоколада.

Следовательно, у Риты и Сумы вместе шоколадок меньше, чем у Джона.

Связанные рабочие листы

Меньше в числовой строке

Чтобы показать знак меньше чем в числовой строке, мы используем пустой кружок, чтобы отметить предельное значение, и указываем стрелкой на заданное условие неравенства. Пустой кружок показывает, что предельное значение не является решением данного неравенства.

Давайте рассмотрим шаги для представления неравенства вида x < 3 на числовой прямой.

Шаг 1 : Найдите «3» в числовой строке и отметьте ее пустым кружком.

Шаг 2 : Неравенство x < 3 показывает, что переменная x может иметь любое значение меньше 3, что означает все значения слева от этого круга. Начиная с пустого круга (предельное значение), вытяните стрелку до левого конца, обозначающую все значения переменной 9.0243 x может быть.

Примечание : Если бы неравенство было «меньше или равно», мы бы заполнили кружок. Закрашенный кружок показывает, что предельное значение также является решением данного неравенства.

Разница между символами сравнения

Подводя итог, сравнение играет важную роль в нашей жизни. Без сравнения трудно показать равенство или неравенство между вещами, которые мы видим вокруг себя.

Интересные факты Британский математик Томас Харриот впервые использовал знак меньше чем (<) в 1631 году в своей книге Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas .

Решенные примеры

Пример 1: Выберите числа меньше 20 из заданного набора чисел.

0, 14, 21, 20, 18, 22, 36, 45, 12, 3, 15, 99, 27

Решение:

0, 14, 18, 12, 3, 15 – все числа < 20,

Пример 2: В аквариуме есть разные виды рыб.

Каких видов рыб меньше 60?

Решение:

Количество гуппи (45), рыбок данио (25) и тигровых барбусов (26) меньше 60.

Example 3: Graph x < 5.

Solution:

Example 4: State whether true or false :

1.   15 < 15
2.  15 < 18
3.   15 < 14
4.  15 < 20

Решение:

1. Ложь
2. Правда
3. Ложь
4. Правда

Практические задачи

1

Выберите возможное значение, удовлетворяющее числу $\lt$10.

10

4

14

20

Правильный ответ: 4
4$\lt$10. Все остальные параметры либо больше, либо равны 10.

2

Выберите правильный граф, который лучше всего описывает числа $\lt$ 4.

(a)

(b)

(c)

(d)

Правильный ответ: (a)
граф чисел $\lt$ 4 должен иметь пустой кружок, отмеченный цифрой 4, и стрелку, начинающуюся с 4 и идущую влево от нее.

3

В корзине A 50 яблок, в корзине B 42 яблока, в корзине C 46 яблок и в корзине D 44 яблока. В какой корзине меньше яблок, чем в корзине D?

Корзина A

Корзина B

Корзина C

Все

Правильный ответ: Корзина B
42 (B) $\lt$ 44 (D) $\lt$ 46 (C) $\lt$ 50 (А). Значит, в корзине B меньше яблок.

4

Выберите утверждение, объясняющее 23 $\lt$ 50.

23 равно 50

23 больше 50

23 меньше 50

23 может быть меньше 900 50 2 равно: 23 меньше 50
Символ «$\lt$» обозначает меньше чем.

Часто задаваемые вопросы

В чем разница между меньше и меньше или равно?

Меньше представлено знаком «<», а меньше или равно представлено знаком «≤». Первый термин означает, что переменная или величина должны иметь значение меньше заданного предела, тогда как «меньше или равно» означает, что переменная или величина должны быть равны или меньше заданного предела.