Звезда фигура геометрическая: Звезда (геометрия) — Википедия – Звезда (геометрическая фигура) — это… Что такое Звезда (геометрическая фигура)?

Звезда (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

Правильная четырёхконечная звезда

Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.

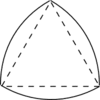
Правильная 8-вершинная звезда, вписанная в правильный 8-угольник

Правильной геометрической звездой можно было бы считать фигуру, вписанную в равносторонний многоугольник, построенный в окружности произвольного радиуса так, чтобы вершины многоугольника совпадали с вершинами звезды. Правильные звёзды могут быть построены с числом сторон не менее пяти. Все звёзды, построенные в многоугольниках с числом сторон 5 и более характеризуются определёнными соотношениями угла между соседними вершинами к углу самих вершин, выраженными двумя целыми числами, в зависимости от чётности числа сторон исходного многоугольника. Если число сторон исходного многоугольника чётное, то соотношение указанных углов равно 2 (двум), то есть угол между соседними вершинами в два раза больше угла самих вершин звёзд с числом вершин 6 и более. Если число сторон исходного многоугольника нечётное, то соотношение угла между соседними вершинами к углу самих вершин звёзд равно 3 (трём). Так например, угол между соседними вершинами пятиконечной звезды (нечётное число сторон исходного многоугольника)равен 108°, а угол самой вершины равен 36°. Отношение 108 к 36 равно трём. Угол между соседними вершинами десятиконечной звезды (чётное число исходного многоугольника)равен 72°, а угол самой вершины равен 36°, т.е отношение 72 к 36 равно 2 (двум). Интересно отметить, что восьмиконечная (восьмивершинная) звезда, построенная путём поворота одного из двух наложенных квадратов на 45 градусов вокруг общего центра, имеет соотношение углов 1,5 (полтора), то есть угол между вершинами составляет 135°, а угол вершины-90°. По-видимому, эту 8-вершинную звезду нельзя отнести к категории правильных геометрических звёзд. Восьмиконечная звезда с обычным соотношением этих углов (2) имеет угол между вершинами 90°, а угол самой вершины составляет 45°. Из каждой правильной геометрической звезды можно выделить четырёхстороннюю фигуру с тремя вершинами в виде пики, имеющей две пары сторон разной длины и три вершины с одинаковым значением угла. Например, упомянутая пятивершинная звезда м.б. образована двумя пиками, угол вершин которых равен 36°, при этом одна из трёх вершин каждой пики оказывается совмещённой с одной из вершин другой пики. Поэтому за счёт наложения вершин каждой пики получается звезда с пятью вершинами. Использование равностороннего треугольника и квадрата для построения правильных 3-конечной и 4-конечной звёзд описанным способом не представляется возможным. Для построения этих звёзд можно использовать соответственно равносторонние шестиугольник и восьмиугольник. При этом можно построить произвольное число трёхконечных и четырёхконечных звёзд, но ни одна из них не будет соответствовать данным соотношениям углов. Таким образом, правильными геометрическими звёздами можно было бы признать остроконечные многоугольники с углами меньше 90°, у которых отношение углов вершин к углам между соседними вершинами равно двум или трём. Таким образом, основным признаком правильной звезды является наличие не менее двух пик в виде четырёхсторонних фигур с тремя равными углами, которые в 2 или 3 раза меньше внешнего угла, образованного сторонами соседних углов.

Каждая вершина правильного n-многоугольника соединяется с m-ной от неё на окружности по часовой стрелке. Звезда, полученная таким образом, обозначается как

{n/m}. При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n-угольник. Её также называют звёздчатым многоугольником, и она является звёздчатой формой соответствующего ей n-угольника.

Соотношение радиусов 2 окружностей правильной звезды с вышеприведённым вариантом построения: внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения сторон соседних лучей) вычисляется по формуле:

cos⁡(πn×m)cos⁡(πn×(m−1)){\displaystyle {\frac {\cos \left({\frac {\pi }{n}}\times m\right)}{\cos \left({\frac {\pi }{n}}\times (m-1)\right)}}}

Звёзды могут быть связными (нераспадающимися едиными многоугольниками), не являясь соединениями других правильных или звёздчатых многоугольников, а могут быть несвязными, распадаясь на несколько одинаковых правильных многоугольников или связных звёзд.

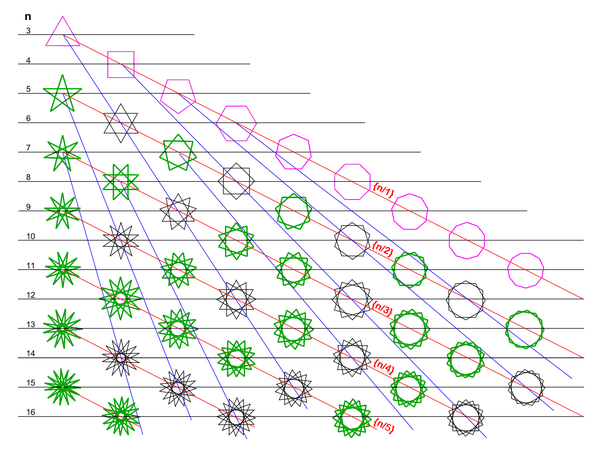Двумерное дискретное множество звёзд.
Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа), см. также Фигуры Лиссажу.
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как этот

В природе[править | править код]

Шахматы[править | править код]

• На шахматной доске в поле 3х3 траектория коня образует восьмиконечную звезду.

Звёздчатые многоугольники — звёздчатые иллюзии

Звезда (геометрия) — это… Что такое Звезда (геометрия)?

Правильная четырёхконечная звезда

Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения. Обычно под звёздами подразумевают фигуры, напоминающие по форме изображение звезды.

Одно из определений

Правильной геометрической звездой можно было бы считать фигуру, вписанную в равносторонний многоугольник, построенный в окружности произвольного радиуса, так чтобы вершины многоугольника совпадали с вершинами звезды. Правильные звёзды могут быть построены с числом сторон не менее пяти. Все звёзды, построенные в многоугольниках с числом сторон 5 и более характеризуются определёнными соотношениями угла между соседними вершинами к углу самих вершин, выраженными двумя целыми числами, в зависимости от числа сторон исходного многоугольника. Если число сторон исходного многоугольника чётное, то соотношение равно 2 (двум), т.е. угол между соседними вершинами в два раза больше угла самих вершин звёзд с числом вершин 6 и более. Если число сторон исходного многоугольника нечётное, то соотношение угла между соседними вершинами к углу самих вершин звёзд равно 3 (трём). Так например, угол между соседними вершинами пятиконечной звезды (нечётное число сторон исходного многоугольника)равен 108 градусов, а угол самой вершины равен 36 градусам. Отношение 108 к 36 равно трём. Угол между соседними вершинами десятиконечной звезды (чётное число исходного многоугольника)равен 72 градусам, а угол самой вершины равен 36 градусам, т.е отношение 72 к 36 равно 2 (двум). Интересно отметить, что восьмиконечная (восьмивершинная) звезда, помимо основного соотношения углов равного 2(двум), построенного путём поворота одного из двух наложенных квадратов на 45 градусов вокруг общего центра, имеет соотношение углов 1,5 (полтора),т.е. угол между вершинами составляет 135 градусов, а угол вершины 45 градусов. По-видимому, эту 8-вершинную зввезду нельзя отнести к категории правильных геометрических звёзд. Восьмиконечная звезда с обычным соотношением этих углов (2) имеет угол между вершинами 90 градусов, а угол самой вершины составляет 45 градусов. Использование равностороннего треугольника и квадрата для построения правильных 3-конечной и 4-конечной звёзд описанным способом не представляется возможным. Для построения этих звёзд можно использовать соответственно равносторонние шестиугольник и восьмиугольник. При этом можно построить произвольное число трёхконечных и четырёхконечных звёзд, но ни одна из них не будет соответствовать данным соотношениям углов.

Другое определение

Другое, отличное от предыдущего, понятие звезды связано со способом построения, который состоит в том, что по кругу симметрично ставятся

n точек и они соединяются между собой, при этом каждая точка соединяется со следующей, m-ной от неё при счёте по кругу, через некоторое количество точек (m — 1) (при m = 1 точки соединяются подряд и получается выпуклый правильный многоугольник). Звезда, полученая таким образом, обозначается символом {n/m}. При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n-угольник. Её также называют звёздчатым многоугольником, и она является звёздчатой формой соответствующего ей n-угольника.

Соотношение радиусов 2 окружностей правильной звезды с вышеприведённым вариантом построения: внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения сторон соседних лучей) вычисляется по формуле:

Звёзды могут быть связными

(нераспадающимися едиными многоугольниками), не являясь соединениями других правильных или звёздчатых многоугольников, а могут быть несвязными, распадаясь на несколько одинаковых правильных многоугольников или связных звёзд.

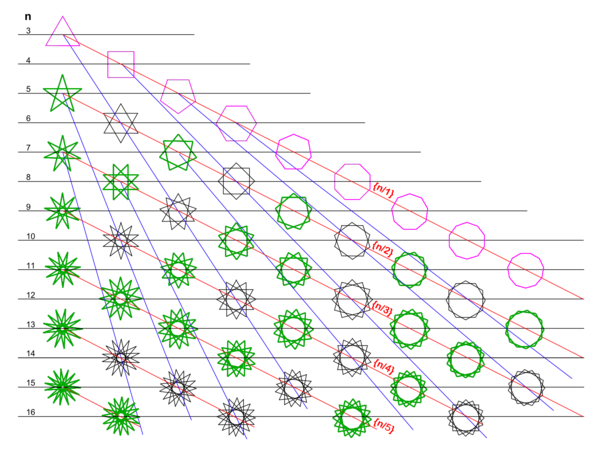Двумерное дискретное множество звёзд.
Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа), см. также Фигуры Лиссажу.
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как этот

Многообразие звёзд

В природе

Шахматы

• На шахматной доске в поле 3х3 траектория коня образует восьмиконечную звезду

См. также

Ссылки

Звёздчатые многоугольники — звёздчатые иллюзии

Звезда (геометрическая фигура) Википедия

Правильная четырёхконечная звезда

Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.

Первое определение

Правильная 8-вершинная звезда, вписанная в правильный 8-угольник

Правильной геометрической звездой можно было бы считать фигуру, вписанную в равносторонний многоугольник, построенный в окружности произвольного радиуса так, чтобы вершины многоугольника совпадали с вершинами звезды. Правильные звёзды могут быть построены с числом сторон не менее пяти. Все звёзды, построенные в многоугольниках с числом сторон 5 и более характеризуются определёнными соотношениями угла между соседними вершинами к углу самих вершин, выраженными двумя целыми числами, в зависимости от чётности числа сторон исходного многоугольника. Если число сторон исходного многоугольника чётное, то соотношение указанных углов равно 2 (двум), то есть угол между соседними вершинами в два раза больше угла самих вершин звёзд с числом вершин 6 и более. Если число сторон исходного многоугольника нечётное, то соотношение угла между соседними вершинами к углу самих вершин звёзд равно 3 (трём). Так например, угол между соседними вершинами пятиконечной звезды (нечётное число сторон исходного многоугольника)равен 108°, а угол самой вершины равен 36°. Отношение 108 к 36 равно трём. Угол между соседними вершинами десятиконечной звезды (чётное число исходного многоугольника)равен 72°, а угол самой вершины равен 36°, т.е отношение 72 к 36 равно 2 (двум). Интересно отметить, что восьмиконечная (восьмивершинная) звезда, построенная путём поворота одного из двух наложенных квадратов на 45 градусов вокруг общего центра, имеет соотношение углов 1,5 (полтора), то есть угол между вершинами составляет 135°, а угол вершины-90°. По-видимому, эту 8-вершинную звезду нельзя отнести к категории правильных геометрических звёзд. Восьмиконечная звезда с обычным соотношением этих углов (2) имеет угол между вершинами 90°, а угол самой вершины составляет 45°. Из каждой правильной геометрической звезды можно выделить четырёхстороннюю фигуру с тремя вершинами в виде пики, имеющей две пары сторон разной длины и три вершины с одинаковым значением угла. Например, упомянутая пятивершинная звезда м.б. образована двумя пиками, угол вершин которых равен 36°, при этом одна из трёх вершин каждой пики оказывается совмещённой с одной из вершин другой пики. Поэтому за счёт наложения вершин каждой пики получается звезда с пятью вершинами. Использование равностороннего треугольника и квадрата для построения правильных 3-конечной и 4-конечной звёзд описанным способом не представляется возможным. Для построения этих звёзд можно использовать соответственно равносторонние шестиугольник и восьмиугольник. При этом можно построить произвольное число трёхконечных и четырёхконечных звёзд, но ни одна из них не будет соответствовать данным соотношениям углов. Таким образом, правильными геометрическими звёздами можно было бы признать остроконечные многоугольники с углами меньше 90°, у которых отношение углов вершин к углам между соседними вершинами равно двум или трём. Таким образом, основным признаком правильной звезды является наличие не менее двух пик в виде четырёхсторонних фигур с тремя равными углами, которые в 2 или 3 раза меньше внешнего угла, образованного сторонами соседних углов.

Каждая вершина правильного n-многоугольника соединяется с m-ной от неё на окружности по часовой стрелке. Звезда, полученная таким образом, обозначается как {n/m}. При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n-угольник. Её также называют звёздчатым многоугольником, и она является звёздчатой формой соответствующего ей n-угольника.

Соотношение радиусов 2 окружностей правильной звезды с вышеприведённым вариантом построения: внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения сторон соседних лучей) вычисляется по формуле:

cos⁡(πn×m)cos⁡(πn×(m−1)){\displaystyle {\frac {\cos \left({\frac {\pi }{n}}\times m\right)}{\cos \left({\frac {\pi }{n}}\times (m-1)\right)}}}

Звёзды могут быть связными (нераспадающимися едиными многоугольниками), не являясь соединениями других правильных или звёздчатых многоугольников, а могут быть несвязными, распадаясь на несколько одинаковых правильных многоугольников или связных звёзд.

Двумерное дискретное множество звёзд.
Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа), см. также Фигуры Лиссажу.
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как этот

Многообразие звёзд

В природе

Шахматы

• На шахматной доске в поле 3х3 траектория коня образует восьмиконечную звезду.

См. также

Ссылки

Звёздчатые многоугольники — звёздчатые иллюзии

Звезда (геометрия)

Звезда — плоская геометрическая фигура, составленная из треугольных лучей, выходящих из общего центра, и сливаются в точке пересечения.

Характеристики

По количеству лучей различают треугольные, четырехугольные и т.д. звезды. Произвольная n-угольные звезда строится следующим образом: строится круг. (Назовем отрезок, пересекающий этот круг не более чем в одной точке, «внешним»). На ней произвольным образом выбирают n точек (назовем их «синими»). Далее за кругом, ограниченным этим кругом, относится n точек (назовем их «красными») так, чтобы любая синяя точка была соединена внешними отрезками ровно с двумя красными, а любая красная точка была соединена двумя внешними отрезками ровно с двумя синими , при этом никакие два из этих отрезков не должны пересекаться, кроме как на концах, и углы между двумя отрезками, исходящими из одной синей точки, — т.н. внешние углы звезды, — должны быть тупыми (следовательно, углы между двумя отрезками , выходящих из одной красной точки, — т.н. внутренние углы звезды, — должны быть острыми).

Звездой будет называться многоугольник, образованный построенными нами внешними отрезками. Очевидно, n-угольные звезда является 2n-угольником. Можно определить n-угольные звезду как 2n-угольник, у которого углы при вершинах поочередно то тупые, то острые.

Круг, на котором строилась звезда, называется базовым; очевидно, базовое кольцо входит в звезды; радиус базового круга является важной характеристикой звезды.

Правильная четырехугольная звезда

Правильной называется звезда, все внутренние углы которой равны и все внешние углы равны.

Фигура, ограниченная двумя отрезками, исходящими из одной красной точки, и дугой базового круга, на которое опирается этот угол, называется лучом звезды. Очевидно:

• количество лучей равна количеству углов звезды (поэтому иногда n-угольные звезду называют n-лучевой)
• звезда является объединение лучей с базовым кругом;
• в правильной звезды прямые стороны всех лучей уровне. (Звезда, у каждого луча которой прямые стороны равны, но прямая сторона одного луча не обязательно равна прямой стороне другого луча, называют неправильные; правильная звезда — частный случай неправильные).

Лучи (в примитивном смысле) с началом в центре базового круга, проходящие через красные точки, называются радиал углов звезды, соответствующих данным красным точкам. Звезда, длины всех радиал которой равны, называется ривнопроменевою.

В полуправильные звезды углы между двумя соседними радиал уровне. В правильной звезды, кроме этого, длины радиал уровне. Таким образом, правильная звезда является неправильные ривнопроменевою звездой.

Примеры

Разновидности звездных многоугольников

См.. также

Звёздчатый многоугольник — Википедия

Материал из Википедии — свободной энциклопедии

Звёздчатый многоугольник — многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника. Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд, среди них пентаграмма, гексаграмма, две гептаграммы, октограмма, декаграмма, додекаграмма. Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их следующего пересечения в точках, которые и являются вершинами звёздчатого многоугольника. Полученый звёздчатый многоугольник будет звёздчатой формой правильного многоугольника, из которого он получен. Вершинами звёздчатого многоугольника будут считаться только точки, в которых сходятся стороны этого многоугольника, но не точки пересечения этих сторон; звёздчатая форма данного многоугольника имеет столько же вершин, сколько он сам. Указанную операцию невозможно проделать с правильным треугольником и квадратом, так как после продления их стороны более не пересекаются; среди правильных многоугольников звёздчатые формы имеют только многоугольники с числом сторон более четырёх. Звёздчатой формой правильного пятиугольника (пентагона) является пентаграмма.

Звёзды могут быть нераспадающимися едиными многоугольниками, не являясь соединениями других правильных или звёздчатых многоугольников (как в случае с пентаграммой), а могут являться таковыми соединениями, примером чему служит звёздчатая форма шестиугольника — гексаграмма), являющаяся соединением двух треугольников.

У правильного многоугольника может быть несколько звёздчатых форм, количество которых зависит от того, сколько раз его стороны пересекаются между собой после их продления, примером чего является семиугольник, имеющий 2 звёздчатые формы (два вида семиконечной звезды).

Количество вершин правильного многоугольника	Количество звёздчатых форм правильного многоугольника	Количество нераспадающихся (связных) звёздных многоугольников среди звёздчатых форм	Количество вершин правильного многоугольника, расположенных между двумя вершинами звёздного многоугольника
5	1	1	1
6	1	0
7	2	2	2; 3
8	2	1	2
9	3	2	1; 3
10	3	1	2
11	4	4	1; 2; 3; 4
12	4	1	4

Двумерное дискретное множество звёзд.
Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа).
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как исходный.

Звезда (геометрическая фигура) Вики

Правильная четырёхконечная звезда

Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.

Первое определение[ | код]

Правильная 8-вершинная звезда, вписанная в правильный 8-угольник

Правильной геометрической звездой можно было бы считать фигуру, вписанную в равносторонний многоугольник, построенный в окружности произвольного радиуса так, чтобы вершины многоугольника совпадали с вершинами звезды. Правильные звёзды могут быть построены с числом сторон не менее пяти. Все звёзды, построенные в многоугольниках с числом сторон 5 и более характеризуются определёнными соотношениями угла между соседними вершинами к углу самих вершин, выраженными двумя целыми числами, в зависимости от чётности числа сторон исходного многоугольника. Если число сторон исходного многоугольника чётное, то соотношение указанных углов равно 2 (двум), то есть угол между соседними вершинами в два раза больше угла самих вершин звёзд с числом вершин 6 и более. Если число сторон исходного многоугольника нечётное, то соотношение угла между соседними вершинами к углу самих вершин звёзд равно 3 (трём). Так например, угол между соседними вершинами пятиконечной звезды (нечётное число сторон исходного многоугольника)равен 108°, а угол самой вершины равен 36°. Отношение 108 к 36 равно трём. Угол между соседними вершинами десятиконечной звезды (чётное число исходного многоугольника)равен 72°, а угол самой вершины равен 36°, т.е отношение 72 к 36 равно 2 (двум). Интересно отметить, что восьмиконечная (восьмивершинная) звезда, построенная путём поворота одного из двух наложенных квадратов на 45 градусов вокруг общего центра, имеет соотношение углов 1,5 (полтора), то есть угол между вершинами составляет 135°, а угол вершины-90°. По-видимому, эту 8-вершинную звезду нельзя отнести к категории правильных геометрических звёзд. Восьмиконечная звезда с обычным соотношением этих углов (2) имеет угол между вершинами 90°, а угол самой вершины составляет 45°. Из каждой правильной геометрической звезды можно выделить четырёхстороннюю фигуру с тремя вершинами в виде пики, имеющей две пары сторон разной длины и три вершины с одинаковым значением угла. Например, упомянутая пятивершинная звезда м.б. образована двумя пиками, угол вершин которых равен 36°, при этом одна из трёх вершин каждой пики оказывается совмещённой с одной из вершин другой пики. Поэтому за счёт наложения вершин каждой пики получается звезда с пятью вершинами. Использование равностороннего треугольника и квадрата для построения правильных 3-конечной и 4-конечной звёзд описанным способом не представляется возможным. Для построения этих звёзд можно использовать соответственно равносторонние шестиугольник и восьмиугольник. При этом можно построить произвольное число трёхконечных и четырёхконечных звёзд, но ни одна из них не будет соответствовать данным соотношениям углов. Таким образом, правильными геометрическими звёздами можно было бы признать остроконечные многоугольники с углами меньше 90°, у которых отношение углов вершин к углам между соседними вершинами равно двум или трём. Таким образом, основным признаком правильной звезды является наличие не менее двух пик в виде четырёхсторонних фигур с тремя равными углами, которые в 2 или 3 раза меньше внешнего угла, образованного сторонами соседних углов.

Каждая вершина правильного n-многоугольника соединяется с m-ной от неё на окружности по часовой стрелке. Звезда, полученная таким образом, обозначается как {n/m}. При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n-угольник. Её также называют звёздчатым многоугольником, и она является звёздчатой формой соответствующего ей n-угольника.

Соотношение радиусов 2 окружностей правильной звезды с вышеприведённым вариантом построения: внешней (на которой лежат вершины углов лучей звезды) и внутренней (на которой лежат точки пересечения сторон соседних лучей) вычисляется по формуле:

cos⁡(πn×m)cos⁡(πn×(m−1)){\displaystyle {\frac {\cos \left({\frac {\pi }{n}}\times m\right)}{\cos \left({\frac {\pi }{n}}\times (m-1)\right)}}}

Звёзды могут быть связными (нераспадающимися едиными многоугольниками), не являясь соединениями других правильных или звёздчатых многоугольников, а могут быть несвязными, распадаясь на несколько одинаковых правильных многоугольников или связных звёзд.

Двумерное дискретное множество звёзд.
Пурпурные — выпуклые многоугольники.
Зелёные — связные звёзды {n/m} (где n и m взаимно простые числа), см. также Фигуры Лиссажу.
Чёрные — не связные звёзды {n/m} (где n и m не взаимно простые числа).
Синие прямые соединяют многоугольник (выпуклый или связную звезду) со всеми не связными звёздами, являющимися соединениями (после поворота) разного количества одинаковых многоугольников, таких же как этот

Многообразие звёзд[ | код]

В природе[ | код]

Шахматы[ | код]

• На шахматной доске в поле 3х3 траектория коня образует восьмиконечную звезду.

См. также[ | код]

Ссылки[ | код]

Звёздчатые многоугольники — звёздчатые иллюзии

Звезда. Золотое сечение (часть 1). Группа аналитиков Точка зрения

Переключение навигации

• О нас
  • О проекте
  • Обратная связь
• Ваше мнение
• Предложить материал
• Журнал изменений

• О нас
  • О проекте
  • Обратная связь
  • Ваше мнение
  • Журнал изменений
• Предложить материал

• Войти
• Регистрация

• Рус
• Eng

• Были:
• Ригден Джаппо,
• Ахура Мазда,
• Осирис,
• Архангел Гавриил,
• Джабраил,
• Агапит Печерский,
• Кетцалькоатль

• Ожидаем:
• Имам Махди,
• Утешитель,
• Святой Дух,
• Майтрейя,
• Калки Аватар,
• Машиах,
• Гэсэр-хан

RGDN.info

• Главная
• О нас
  • О проекте
  • Обратная связь
• Ваше мнение
• Предложить материал
• Журнал изменений
• Исконные Знания
  • Беседы с И.М. Даниловым
  • Книги
  • Истина на всех одна
  • Иллюзия и Путь
  • Жизнь
  • Сознание и Личность. От заведомо мёртвого к вечно живому
• Пророчества
• Религии
  • Христианство
  • Ислам
  • Буддизм
  • Индуизм
  • Иудаизм
  • Зороастризм
• Символика и мифология
  • Символика и Мифология
  • Астрономия
  • Мир Пирамид
  • Интересные места
• !?
  • Архонты. Тайные хозяева мира.
  • Кандук. Нечистая сила.
• Новости
• Видео
• Статьи
• Отзывы