Арифметика | Elixir | CodeBasics
В Эликсир есть два вида чисел — целые и с плавающей точкой.
Целые числа могут быть представлены разными способами. В разных системах исчисления: в десятичной, шестнадцатеричной, восьмеричной и двоичной:
42 0x2A 0o52 0b101010
В экспоненциальном виде:
0.42e2
Для больших чисел можно использовать символ подчеркивания между разрядами для удобства чтения:
100_500 1_000_000
Числа с плавающей точкой реализованы по стандарту IEEE 754, как и в большинстве других языков. Это значит, что их точность ограничена, и при некоторых операциях возможна потеря точности:
0.1 + 0.2 # 0.30000000000000004
Для целых чисел, и чисел с плавающей точкой реализованы обычные арифметические операции:
20 + 22 # 42 20.0 + 22 # 42.0 50 - 8.0 # 42.0 2 * 16 # 32 4 * 16.0 # 64.0 128 / 2 # 64.0 64.0 / 4.0 # 16.0
Операторы + - * возвращают целое число, если оба аргумента целые, и число с плавающей точкой, если хотя бы один из аргументов с плавающей точкой.
/ всегда возвращает число с плавающей точкой.Еще есть оператор целочисленного деления div и оператор взятия остатка rem:
div(42, 2) # 21 div(45, 2) # 22 rem(42, 2) # 0 rem(45, 2) # 1
Задание
Реализуйте функцию do_math(a, b), которая принимает два числа, и выводит на экран:
- результат деления суммы первого и второго числа на второе число
- результат целочисленного деления первого числа на второе
- остаток от деления второго числа на первое
Каждый результат выводится на отдельной строке.
defmodule Solution do
def do_math(a, b) do
# TODO реализация
end
end
Упражнение не проходит проверку — что делать? 😶Если вы зашли в тупик, то самое время задать вопрос в «Обсуждениях». Как правильно задать вопрос:
- Обязательно приложите вывод тестов, без него практически невозможно понять что не так, даже если вы покажете свой код. Программисты плохо исполняют код в голове, но по полученной ошибке почти всегда понятно, куда смотреть.

Тесты устроены таким образом, что они проверяют решение разными способами и на разных данных. Часто решение работает с одними входными данными, но не работает с другими. Чтобы разобраться с этим моментом, изучите вкладку «Тесты» и внимательно посмотрите на вывод ошибок, в котором есть подсказки.
Мой код отличается от решения учителя 🤔Это нормально 🙆, в программировании одну задачу можно выполнить множеством способов. Если ваш код прошел проверку, то он соответствует условиям задачи.
В редких случаях бывает, что решение подогнано под тесты, но это видно сразу.
Прочитал урок — ничего не понятно 🙄Создавать обучающие материалы, понятные для всех без исключения, довольно сложно. Мы очень стараемся, но всегда есть что улучшать. Если вы встретили материал, который вам непонятен, опишите проблему в «Обсуждениях». Идеально, если вы сформулируете непонятные моменты в виде вопросов. Обычно нам нужно несколько дней для внесения правок.
Кстати, вы тоже можете участвовать в улучшении курсов: внизу есть ссылка на исходный код уроков, который можно править прямо из браузера.
Полезное
←Предыдущий
Следующий→
Нашли ошибку? Есть что добавить? Пулреквесты приветствуются https://github.com/hexlet-basics
Работа с числами и математическими методами в JavaScript
Подборка самых важных и часто используемых методов работы с числами и математическими функциями в JavaScript с примерами.
Вам будет проще разобраться с этими методами, если вы уже знакомы с типами данных в JavaScript.
Основы работы с числами
- В JavaScript существует всего один числовой тип. Таким образом, значения
5и5.12принадлежат к одному и тому же типу. - JS использует формат 64-битных чисел двойной точности по стандарту IEEE 754.
Это означает, что все числа в JavaScript имеют плавающую запятую. Пусть вас не обманывает запись var x = 1, на самом деле это float, равный 1.. 0
0
Если вы действительно хотите разобраться в особенностях чисел в JS, загляните сюда:
- ECMAScript® 2018 Language Specification. Number Type
- Here is what you need to know about JavaScript’s Number type
А в этой статье мы сконцентрируемся на методах работы со значениями типа Number.
Создание чисел
Объявить переменную, содержащую числовое значение, можно с помощью ключевых слов let (если она будет изменяться) или const (если не будет). Перед отрицательными числами ставится -:
const PI = 3.14 const x = 1 const n = -10
Единственный 0 в целой или дробной части числа можно не указывать, но все же стоит это делать для лучшей читаемости кода.
const y = 0.15 const z = .90 const t = 5.
Будьте осторожны с ограничениями по размеру:
const r = 9999999999999999 // 10000000000000000 const l = 999999999999999999999999 // 1e+25 const i = Infinity // Infinity - бесконечность со знаком +
Конвертация в число:
const str = '24.23' const bin = '110110' const short = +str // 24.23 const num = Number(str) // 24.23 // второй аргумент – основание системы счисления const b = Number.parseInt(bin, 2) // 54
Можно работать и в других системах счисления:
const hex = 0xff // 255 const octal = 012 // 10 const betterOctal = 0o23 // 19 - способ работы с восьмеричной системой, введенный в ES6 const binary = 0b1101 // 13
Важные принципы
- все числа – с плавающей точкой;
- все числа имеют один тип — «number»;
- как и в других языках, в JS существуют ограничения по максимальному размеру и точности чисел.
Основные методы
Безопасные числа
Скорее всего, вы хотите, чтобы значение числа всегда оставалось тем же самым, что вы ему задали. Но если вы используете в коде, к примеру, число 900719925474099164 оно превратится в 900719925474099200. Дело в том, что оно выходит за пределы так называемого безопасного диапазона.
Узнать эти пределы можно, обратившись к свойствам объекта Number MIN_SAFE_INTEGER и MAX_SAFE_INTEGER. А с помощью функции Number.isSafeInteger можно определить, является ли число безопасным.
// константы минимального и максимального безопасных чисел Number.MAX_SAFE_INTEGER // 9007199254740991 Number.MIN_SAFE_INTEGER // -9007199254740991 // не путайте их с минимальным и максимальным числом Number.MAX_VALUE // 1.7976931348623157e+308 Number.MIN_VALUE // 5e-324 // проверка, находится ли число в безопасном диапазоне Number.isSafeInteger(1.7976931348623157e+308) // false Number.isSafeInteger(9007199254740991) // true
Целое ли число?
Используйте метод isInteger
Number. Если число не имеет десятичной части, он возвращает true. Обратите внимание, что числа с пустой десятичной частью автоматически конвертируются в целые.Number.isInteger(5) // true Number.isInteger(5 / 2) // false Number.isInteger(5.00) // true
Есть более короткий, но менее читаемый способ проверить, целое ли число:
5 % 1 === 0 // true 5.5 % 1 === 0 // false
Изменение количества знаков после запятой
Используйте метод Number.toFixed, который принимает количество знаков десятичной части, а возвращает строковое представление числа в нужном формате.
const a = 5.6710142 const b = 0.993 a.toFixed(2) // '5.67' a.toFixed(1) // '5.7' b.toFixed() // '1' b.toFixed(20) // '0.99299999999999999378' b.toFixed(30) // некоторые браузеры не поддерживают более 20 символов
Также можно воспользоваться методом Number.toPrecision, которому нужно передать количество значащих цифр числа. На выходе также получается строка:
const a = 5.6710142 const b = 0.993 a.toPrecision(2) // '5.7' a.toPrecision(1) // '6' b.toPrecision() // 0.993 b.toPrecision(20) // 0.99299999999999999378
Преобразование в экспоненциальную форму
Экспоненциальная форма известна также известна как научная нотация. Для преобразования существует специальный метод toExponential. Его единственный необязательный параметр – количество цифр после запятой.
const x = 25893210 const y = 33.1894 const z = 10000000 const p = x.toExponential() // '2.589321e+7' y.toExponential() // '3.31894e+1' z.toExponential() // '1e+7' z.toExponential(2) // '1.00e+7' // обратное преобразование console.log(p) // '2.589321e+7' Number(p) // 25893210 parseFloat(p) // 25893210
Глобальные функции для работы с числами и методы Number
Вы, возможно, знаете, что существуют глобальные функции вроде parseInt, но только что мы использовали Number.parseInt().
Дело в том, что последний стандарт JavaScript пытается модуляризировать глобальные сущности и обновляет некоторые существующие модули. Например, метод
Например, метод isNaN отличается от нового метода Number.isNaN.
Работа с большими числами
Тип BigInt на данный момент находится в статусе предложения и недоступен в ряде браузеров. Большие числа создаются путем добавления n в конец числа или с помощью конструктора.
const large = 9007199254740991n
const constructed = BigInt(9007199254740991) // 9007199254740991n
const fromString = BigInt('9007199254740991') // 9007199254740991n
const safe = BigInt(Number.MAX_SAFE_INTEGER) // 9007199254740991n
safe + 3n // 9007199254740994n
large + safe // 18014398509481982nПока нет полной поддержки BigInt, вы можете использовать библиотеку bignumber.js.
Преобразование в другую систему счисления
Перевести число из десятичной системы в другую можно с помощью метода toString, указав желаемое основание системы (от 2 до 36). Для обратного преобразования используйте метод parseInt:
const num = 3241 const bin = num.toString(2) // '110010101001' num.toString(8) // '6251' num.toString(16) // 'ca9' num.toString(10) // '3241' Number.parseInt(bin, 2) // 3241
Методы числовых литералов
Возможно, вы попытались применить какой-нибудь метод к числовому литералу (23.toString(2)) и получили синтаксическую ошибку. Это связано со специфическим представлением чисел в JavaScript. Валидная форма для числа 23 — 23. или 23.0 (0 в дробной части можно не указывать).
Когда вы пишете 23.toString(2) JavaScript считает эту запись числом и не понимает, что вызывается метод.
Решением может быть использование скобок или двух точек для указания дробной части (хотя это довольно непонятная запись):
(23).toString(2) // "10111" 23..toString(2)
Не число – это число
Подробное объяснение этого феномена можно найти в статье JS Essentials: Types & Data Structures.
Коротко говоря, NaN является объектом класса Number, но определяется как результат математических операций, значение которых количественно число не является. Правильнее было бы назвать его Invalid Number.
Правильнее было бы назвать его Invalid Number.
NaN превращает все, с чем имеет дело, в NaN.
const a = 5 + NaN // NaN
Проверка на NaN
Это единственное значение в JavaScript, которое не равно самому себе. Мы можем использовать это, применяя проверку true, то x – это NaN.
Помимо этого можно использовать методы Object.is, isNaN и новый метод Number.isNaN. Обратите внимание, два последних метода ведут себя по-разному с нечисловыми значениями.
NaN == NaN // false
NaN === NaN // false
Object.is(NaN, NaN) // true
isNaN(NaN) // true
isNaN('abc') // true
Number.isNaN(NaN) // true
Number.isNaN('abc') // false
Number.isNaN(+'abc') // trueСпособы округления чисел
const x = 5.921 // округление вниз Math.floor(x) // 5 // округление вверх Math.ceil(x) // 6 // округление по правилам математики Math.round(x) // 6 Math.round(5.5) // 6 // до нужного количества цифр после точки x.toFixed(2) // 5.92 x.toPrecision(2) // 5.9 // битовый сдвиг // работает быстрее, чем Math.floor // но очень неочевидно для ваших коллег x >> 0 // 5
Возведение в степень
В JavaScript существует специальный оператор степени – **. Также можно воспользоваться методом Math.pow.
2 ** 2 // 4 let x = 2 x ** = 4 // 16 Math.pow(2, 4) // 16
Генерация случайного числа
Метод Math.random генерирует дробное число в диапазоне от 0 (включая) до 1 (не включая).
Math.random() // 0.7610368478059286
// генерация числа в диапазоне от 0 до 9
// битовый сдвиг работает как Math.floor
Math.random() * 10 >> 0
Math.floor(Math.random() * 10)
// генерация числа в диапазоне [x, y)
const getRandom = (min, max) =>
Math. floor(Math.random() * (max - min + 1)) + min;
floor(Math.random() * (max - min + 1)) + min;Вот небольшой пример: создадим сет – набор уникальных значений, заполним его случайными числами с помощью метода getRandom и отсортируем:
for (let i of Array(500)) {
values.add(getRandom(1, 10))
}
[...values].sort((a, b) => a - b)
// [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ]Математические функции
В модуле Math очень много полезных методов, которые вы можете найти в документации. Все они имеют довольно очевидный принцип работы.
Полезные ссылки
- JavaScript Essentials – серия простых и полезных статей об основных методах и приемах работы в Javascript.
- Спецификация ECMAScript 2018.
- Документация по объекту Number.
- Документация по модулю Math.
Практика работы с числами
Несколько полезных челленджей на codewars.com.
- Преобразуйте число в строку
- Квадрат каждой цифры
- Это треугольник?
- Игра с цифрами
- Кратно 3 или 5
Перевод статьи JavaScript Essentials: Numbers and Math.
Полезные ресурсы для начинающего JavaScript-разработчика
- Где JavaScript джуну получать тестовые задания для практики?
- Путь JavaScript Junior: подборка лучших ресурсов для обучения
- Огромный видеокурс по основам JavaScript от freeCodeCamp
- Тест: насколько хорошо вы знаете JavaScript
javascript — Оператор по модулю — Переполнение стека
Оператор «мод» в компьютерных языках — это просто остаток. За например,
17 мод 3 = 2
потому что
17/3 = 5 рем 2
что в свою очередь означает
17 = 3 * 5 + 2
При использовании отрицательных чисел возникают некоторые сложности, но это обычно не требуется.
В математике (теории чисел) этот термин используется немного по-другому. «модуль» на самом деле не остаток, а число, которое вы деление на; а «мод» — это не оператор, а метка, сообщающая «в в каком смысле две величины считаются конгруэнтными или равными». например, мы бы сказали
17 = 11 (мод.3)
(читается как «17 сравнимо с 11 по модулю 3»), что означает, что 17 и 11 оба оставляют ОДИНАКОВЫЙ остаток при делении на 3. Вы, вероятно, не будете см. это использование, если вы только читаете о программировании, но это стоит знать, если вы глубже изучите математику, стоящую за этим.
Если два числа b и c обладают тем свойством, что их разность b-c равна целое делится на число m (т. е. (b-c)/m — целое число), тогда говорят, что b и c «конгруэнтны по модулю m». Число м называется модулем, а утверждение «b сравнимо с c (по модулю m)» математически записывается как
b=c (mod m). (1) Если b-c не делится на m целиком, то оно говорят, что «b не сравнимо с c (по модулю m)», что записывается как
.б≢в (мод м). (2) Явное выражение «(mod m)» иногда опускается, когда модуль m понимается по контексту, поэтому в таких случаях необходимо соблюдать осторожность. принято, чтобы не путать символ = со знаком эквивалентности.
Величину b иногда называют «основной», а величину c —
называется остатком или остатком. Существует несколько видов остатков.
Общий остаток определяется как неотрицательный и меньше m, в то время как
минимальный остаток равен c или cm, в зависимости от того, что меньше по абсолютной величине
стоимость.
Существует несколько видов остатков.
Общий остаток определяется как неотрицательный и меньше m, в то время как
минимальный остаток равен c или cm, в зависимости от того, что меньше по абсолютной величине
стоимость.
CongruenceClockMinutes Арифметика конгруэнтности, пожалуй, наиболее знакома как обобщение арифметики часов. Так как есть 60 минут в час, «минутная арифметика» использует модуль m = 60. Если один начинается в 40 минут первого часа, а затем ждет еще 35 минут, 40+35=15 (mod 60), поэтому текущее время будет через 15 минут после начала. (следующий) час.
CongruenceClockHours Аналогично, «часовая арифметика» на 12-часовых часах использует модуль m = 12, поэтому 10 часов (утра) плюс пять часов дают 10+5=3 (mod 12), или 3 часа (pm) 9′ (mod m), то важные свойства соответствия включают следующее, где => означает «подразумевает»:
Эквивалентность: a=b (mod 0)=>a=b (что можно рассматривать как определение).
Определение: либо a=b (mod m), либо a≢b (mod m).

Рефлексивность: а=а (mod m).
Симметрия: a=b (mod m)=>b=a (mod m).
Транзитивность: a=b (mod m) и b=c (mod m)=>a=c (mod m).
9’r+rsm)m, (7) так что свойства верны.Сравнения применимы и к дробям. Например, обратите внимание, что
2×4=1 3×3=2 6×6=1 (мод. 7), (8) итак
1/2=4 1/4=2 2/3=3 1/6=6 (мод. 7). (9) Чтобы найти p/q (mod m) где (q,m)=1 (т.е. q и m взаимно просты), используйте алгоритм похоже на жадный алгоритм. Пусть q_0=q и найдите
p_0=[m/(q_0)], (10) где [x] — функция потолка, затем вычислить
q_1=q_0p_0 (mod m). (11) Итерировать до тех пор, пока q_n=1, затем 9(n-1)p_i (mod m). (12) Этот метод работает всегда для m простых, а иногда даже для m составных. Однако для составное m, метод может дать сбой, достигнув 0 (Conway and Guy 1996).
Нахождение дробного сравнения эквивалентно решению соответствующее линейное уравнение сравнения
ось=b (mod m). (13) Дробное сравнение единичной дроби есть известный как модульная инверсия.
 Дробное соответствие можно найти в
Язык Wolfram с помощью следующей функции:
Дробное соответствие можно найти в
Язык Wolfram с помощью следующей функции:FractionalMod[r_Rational, m_Integer] := Mod[ Числитель[r]PowerMod[Знаменатель[r], -1, m], m] или использование недокументированного синтаксиса PolynomialMod[r, m] для r явного рационального количество.
Как выполнять математические операции в JavaScript с помощью операторов
Введение
Математические операции относятся к наиболее фундаментальным и универсальным функциям любого языка программирования. В JavaScript числа часто используются для общих задач, таких как определение размера окна браузера, получение окончательной цены денежной транзакции и расчет расстояния между элементами в документе веб-сайта.
Хотя знание математики на высоком уровне не является необходимым условием для того, чтобы быть способным разработчиком, важно знать, какие типы операций доступны в JavaScript и как использовать математику в качестве инструмента для выполнения практических задач.
В отличие от других языков программирования, JavaScript имеет только один числовой тип данных; например, нет различия между целыми числами (положительными или отрицательными целыми числами) и числами с плавающей запятой (числа с десятичной точкой).

В этом руководстве мы рассмотрим арифметические операторы, операторы присваивания и порядок операций, используемых с числовыми типами данных JavaScript.
Арифметические операторы
Арифметические операторы — это символы, обозначающие математическую операцию и возвращающие значение. В уравнении
3 + 7 = 10+— это синтаксис, означающий сложение.В JavaScript есть много знакомых операторов из базовой математики, а также несколько дополнительных операторов, специфичных для программирования.
Вот справочная таблица арифметических операторов JavaScript.
Оператор Синтаксис Пример Определение Дополнение +х + уСумма хиуВычитание -х - уРазница между xиyУмножение *х * уПродукт xиyОтдел /х/уЧастное xиyМодуль %х % уОстаток х/уВозведение в степень **х ** уxдоyмощностьПриращение ++х++xплюс одинУменьшение --х--xминус одинВ этой статье мы более подробно рассмотрим каждый из этих операторов.

Сложение и вычитание
Сложение и операторы вычитания доступны в JavaScript и могут использоваться для нахождения суммы и разности числовых значений. В JavaScript есть встроенный калькулятор, а математические операции можно выполнять прямо в консоли.
Мы можем выполнить простое сложение с числами, например сложить
10и20, используя знак плюс (+).10 + 20
Помимо выполнения математических операций с простыми числами, мы также можем присваивать числа переменным и выполнять те же вычисления. В этом случае мы присвоим числовые значения
xиyи поместите сумму вz.// Присвоить значения x и y пусть х = 10 пусть у = 20 // Добавляем x и y и присваиваем сумму z пусть г = х + у console.log(z)
Точно так же мы используем знак минус (
-) для вычитания чисел или переменных, представляющих числа.
// Присвоить значения x и y пусть х = 10 пусть у = 20 // Вычитаем x из y и присваиваем разницу z пусть г = у - х console.log(z)
Мы также можем складывать и вычитать отрицательные числа и числа с плавающей запятой (десятичные).
// Присвоить значения x и y пусть х = -5,2 пусть у = 2,5 // Вычитаем y из x и присваиваем разницу z пусть г = х - у console.log(z)
Одна интересная вещь, о которой следует помнить в JavaScript, — это результат добавления числа и строки.
1 + 1должно равняться2, но это уравнение даст неожиданные результаты.пусть х = 1 + '1' console.log(x) тип х
11 'строка'
Вместо сложения двух чисел JavaScript преобразует весь оператор в строку и соединит их вместе. Важно быть осторожным с динамически типизированной природой JavaScript, так как это может привести к нежелательным результатам.
Распространенной причиной использования сложения или вычитания в JavaScript является прокрутка до идентификатора минус высота в пикселях фиксированной панели навигации.

функция scrollToId() { константа navHeight = 60 window.scrollTo(0, window.pageYOffset - navHeight) } window.addEventListener('hashchange', scrollToId)В приведенном выше примере щелчок по идентификатору приведет к прокрутке на 60 пикселей выше идентификатора.
Сложение и вычитание — два самых распространенных математических уравнения, которые вы будете использовать в JavaScript.
Умножение и деление
Операторы умножения и деления также доступны в JavaScript и используются для нахождения произведения и частного числовых значений.
Звездочка (
*) используется для обозначения оператора умножения.// Присвоить значения x и y пусть х = 20 пусть у = 5 // Умножаем x на y, чтобы получить произведение пусть г = х * у console.log(z)
Умножение может использоваться для расчета цены товара после применения налога с продаж.
const price = 26,5 // Цена товара до налогообложения const taxRate = 0,082 // налоговая ставка 8,2% // Рассчитываем сумму после уплаты налогов с точностью до двух знаков после запятой пусть totalPrice = цена + цена * налоговая ставка totalPrice.
 toFixed(2)
console.log('Total:', totalPrice)
toFixed(2)
console.log('Total:', totalPrice) Total: 28,67
Косая черта (
/) используется для представления оператора деления.// Присвоить значения x и y пусть х = 20 пусть у = 5 // Делим y на x, чтобы получить частное пусть г = х / у console.log(z)
Деление особенно полезно при подсчете времени, например при определении количества часов в количестве минут или при подсчете процента правильных ответов, выполненных в тесте.
Модуль
Один арифметический оператор, который немного менее известен, — это оператор модуля (иногда известный как модуль), который вычисляет остаток от частного после деления. Модуль представлен знаком процента (
%).Например, мы знаем, что
3входит в9ровно три раза, и остатка нет.Мы можем использовать оператор по модулю, чтобы определить, является ли число четным или нечетным, как показано в этой функции:
// Инициализировать функцию для проверки четности числа const isEven = (x) => { // Если остаток после деления на два равен 0, возвращаем true если (х% 2 === 0) { вернуть истину } // Если число нечетное, возвращаем false вернуть ложь } // Проверяем число isEven(12)В приведенном выше примере
12делится без остатка на2, поэтому это четное число.
Часто в программировании по модулю используется в сочетании с условными операторами для управления потоком. 95, написан так:
10 ** 5
100000
10 ** 5представляет собой то же самое, что10, умноженные на10Пять раз:10 * 10 * 10 * 10 10 10. 100136
Другой способ записать это с помощью метода
Math.pow().Math.pow(10, 5)
100000
Использование оператора возведения в степень — это краткий способ нахождения степени заданного числа, но, как обычно, важно придерживаться стиля вашей кодовой базы, когда выбор между методом и оператором.
Увеличение и уменьшение
Увеличение и уменьшение операторы увеличивают или уменьшают числовое значение переменной на единицу. Они представлены двумя знаками «плюс» (
++) или двумя знаками «минус» (—) и часто используются с циклами.
Обратите внимание, что операторы увеличения и уменьшения можно использовать только для переменных; попытка использовать их для необработанного числа приведет к ошибке.
Uncaught ReferenceError: Недопустимое левое выражение в постфиксной операции
Операторы инкремента и декремента могут классифицироваться как префиксные или постфиксные операции, в зависимости от того, стоит ли оператор до или после переменной.
Во-первых, мы можем ввести приращение префикса с помощью
++x.// Установить переменную пусть х = 7 // Используем операцию увеличения префикса пусть префикс = ++x console.log(prefix)
Значение
xбыло увеличено на единицу. Чтобы увидеть разницу, мы проверим инкремент постфикса су++.// Установить переменную пусть у = 7 // Используем операцию увеличения префикса пусть постфикс = у++ console.log(postfix)
Значение
yне было увеличено в постфиксной операции. Это связано с тем, что значение не будет увеличиваться до тех пор, пока выражение не будет вычислено. Выполнение операции дважды приведет к увеличению значения.
Это связано с тем, что значение не будет увеличиваться до тех пор, пока выражение не будет вычислено. Выполнение операции дважды приведет к увеличению значения.пусть у = 7 у++ у++ console.log(y)
Оператор увеличения или уменьшения чаще всего встречается в цикле. В этом
для примера цикла, мы выполним операцию десять раз, начиная с0и увеличивая значение на1с каждой итерацией.// Запустить цикл десять раз для (пусть я = 0; я < 10; я ++) { console.log(я) }0 1 2 3 4 5 6 7 8 9
В приведенном выше коде показана итерация цикла, который достигается с помощью оператора приращения.
Мы можем рассматривать
x++как сокращение дляx = x + 1иx--как сокращение дляx = x - 1.Одним из наиболее часто используемых операторов является оператор присваивания , который мы уже видели и который представлен знаком равенства (
=). Мы используем
Мы используем =, чтобы присвоить значение справа переменной слева.// Присвоить 27 переменной age let age = 27
Помимо стандартного оператора присваивания, в JavaScript есть составных оператора присваивания , которые объединяют арифметический оператор с
=.Например, оператор сложения начнет с исходного значения и добавит новое значение.
// Присвоить 27 переменной age пусть возраст = 27 возраст += 3 console.log(age)
В этом случае
age += 3равносильно записиage = age + 3.Все арифметические операторы можно комбинировать с присваиванием для создания составных операторов присваивания. Ниже приведена справочная таблица операторов присваивания в JavaScript.
Оператор Синтаксис Назначение =Дополнительное назначение +=Назначение вычитания -=Назначение умножения *=Назначение отдела /=Оставшееся назначение %=Возведение в степень **=Составные операторы присваивания часто используются с циклами, подобно инкрементации и декрементации, и используются, когда необходимо повторить или автоматизировать уравнения.

Приоритет оператора
Хотя мы читаем слева направо, операторы будут оцениваться в порядке старшинства, как и в обычной математике.
В следующем примере умножение имеет более высокий приоритет, чем сложение, которое определяет результат уравнения.
// Сначала умножьте 3 на 5, затем прибавьте 10 10 + 3 * 5
Если вместо этого мы хотели бы сначала выполнить операцию сложения, мы должны сгруппировать ее в круглые скобки, которые всегда имеют наивысший приоритет.
// Сначала сложите 10 и 3, затем умножьте на 5 ;(10 + 3) * 5
Ниже приведена справочная таблица приоритетов арифметических операций в JavaScript, от высшего к низшему. Для инкрементации и декрементации постфикс имеет более высокий приоритет, чем префикс.
Увеличение/уменьшение, умножение/деление и сложение/вычитание имеют одинаковый уровень приоритета.
Оператор Синтаксис Скобки ()Приращение ++Уменьшение --Возведение в степень **Умножение *Отдел /Дополнение +Вычитание -Приоритет оператора включает не только арифметические операторы, но и операторы присваивания, логические операторы, условные операторы и многое другое.



 23'
const bin = '110110'
const short = +str // 24.23
const num = Number(str) // 24.23
// второй аргумент – основание системы счисления
const b = Number.parseInt(bin, 2) // 54
23'
const bin = '110110'
const short = +str // 24.23
const num = Number(str) // 24.23
// второй аргумент – основание системы счисления
const b = Number.parseInt(bin, 2) // 54 isInteger(5 / 2) // false
Number.isInteger(5.00) // true
isInteger(5 / 2) // false
Number.isInteger(5.00) // true toPrecision(20) // 0.99299999999999999378
toPrecision(20) // 0.99299999999999999378 toString(2) // '110010101001'
num.toString(8) // '6251'
num.toString(16) // 'ca9'
num.toString(10) // '3241'
Number.parseInt(bin, 2) // 3241
toString(2) // '110010101001'
num.toString(8) // '6251'
num.toString(16) // 'ca9'
num.toString(10) // '3241'
Number.parseInt(bin, 2) // 3241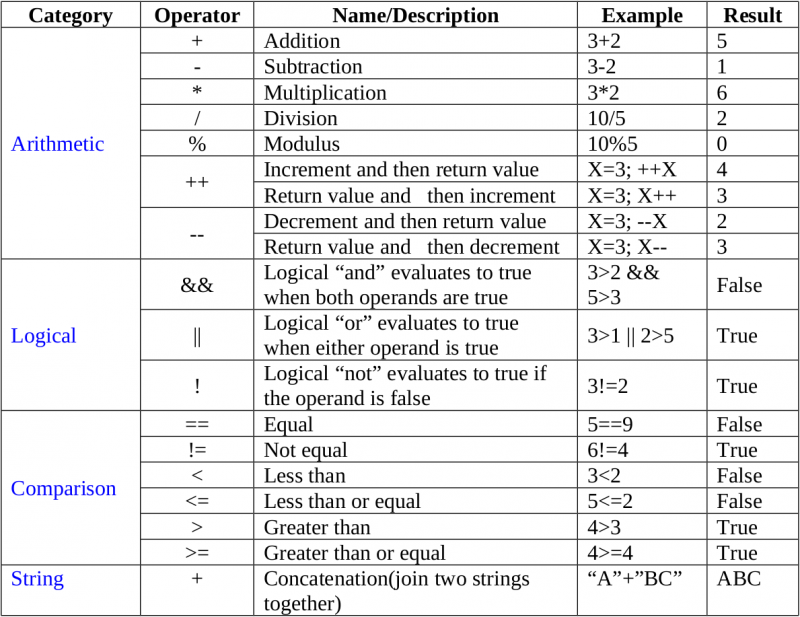 ceil(x) // 6
// округление по правилам математики
Math.round(x) // 6
Math.round(5.5) // 6
// до нужного количества цифр после точки
x.toFixed(2) // 5.92
x.toPrecision(2) // 5.9
// битовый сдвиг
// работает быстрее, чем Math.floor
// но очень неочевидно для ваших коллег
x >> 0 // 5
ceil(x) // 6
// округление по правилам математики
Math.round(x) // 6
Math.round(5.5) // 6
// до нужного количества цифр после точки
x.toFixed(2) // 5.92
x.toPrecision(2) // 5.9
// битовый сдвиг
// работает быстрее, чем Math.floor
// но очень неочевидно для ваших коллег
x >> 0 // 5 floor(Math.random() * (max - min + 1)) + min;
floor(Math.random() * (max - min + 1)) + min; 3)
3)

 Дробное соответствие можно найти в
Язык Wolfram с помощью следующей функции:
Дробное соответствие можно найти в
Язык Wolfram с помощью следующей функции:



 toFixed(2)
console.log('Total:', totalPrice)
toFixed(2)
console.log('Total:', totalPrice) 

 Это связано с тем, что значение не будет увеличиваться до тех пор, пока выражение не будет вычислено. Выполнение операции дважды приведет к увеличению значения.
Это связано с тем, что значение не будет увеличиваться до тех пор, пока выражение не будет вычислено. Выполнение операции дважды приведет к увеличению значения. Мы используем
Мы используем 
