Длина высота широта – Как рассчитать протяженность материка 🚩 длина параллели в градусах 🚩 Гуманитарные науки — Вебджем.рф

Содержание

Система координат — Википедия

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.

В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты[править | править код]

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y):{\displaystyle (x,y):}

x{\displaystyle x} — расстояние от точки P до оси y с учетом знака
y{\displaystyle y} — расстояние от точки P до оси x с учетом знака

В пространстве необходимы уже три координаты (x,y,z):{\displaystyle (x,y,z):}

x{\displaystyle x} — расстояние от точки P до плоскости yz
y{\displaystyle y} — расстояние от точки P до плоскости xz
z{\displaystyle z} — расстояние от точки P до плоскости xy

Полярные координаты[править | править код]

Полярные координаты.

В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox.

В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.

Цилиндрические координаты[править | править код]

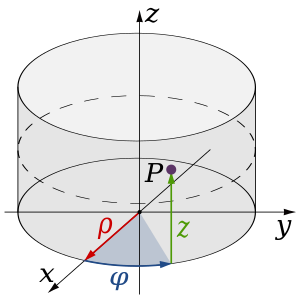Цилиндрические координаты.

Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой (r,φ,z).{\displaystyle (r,\varphi ,z).} В терминах декартовой системы координат,

0⩽r{\displaystyle 0\leqslant {r}} (радиус) — расстояние от оси z до точки P,
0⩽φ<360∘{\displaystyle 0\leqslant \varphi <360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy.
z{\displaystyle z} (высота) равна декартовой z-координате точки P.

Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ, для второй (угловой, или азимутальной) — обозначение θ, для третьей координаты — обозначение h.

Полярные координаты имеют один недостаток: значение φ не определено при r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z, совпадающей с осью цилиндра) имеет уравнение x2+y2=R2,{\displaystyle x^{2}+y^{2}=R^{2},} тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R.

Сферические координаты[править | править код]

$x^{2}+y^{2}=R^{2},$ Сферические координаты.

Сферические координаты — трёхмерный аналог полярных.

В сферической системе координат расположение точки P определяется тремя компонентами: (ρ,φ,θ).{\displaystyle (\rho ,\varphi ,\theta ).} В терминах декартовой системы координат,

0⩽ρ{\displaystyle 0\leqslant \rho } (радиус) — расстояние от точки P до полюса,
0⩽φ⩽360∘{\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P, на плоскость xy.
0⩽θ⩽180∘{\displaystyle 0\leqslant \theta \leqslant 180^{\circ }} (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P.

Примечание: в литературе иногда азимут обозначается θ, а полярный угол — φ. Иногда для радиальной координаты используется r вместо ρ. Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z, а от плоскости xy; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.

Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).

Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ, повернуть его на угол θ вокруг оси y в направлении положительной полуоси x, и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y.

Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как x2+y2+z2=R2,{\displaystyle x^{2}+y^{2}+z^{2}=R^{2},} тогда как в сферических координатах оно становится намного проще: ρ=R.{\displaystyle \rho =R.}

Другие распространённые системы координат[править | править код]

Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса^[1].
Барицентрические координаты были впервые введены в 1827 году А. Мебиусом, решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника. Они аффинно инвариантны, представляют собой частный случай общих однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве Eⁿ, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса^[2].
Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С₁ и С₂, через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P, которая не лежит на этой прямой, определяется углами PC₁C₂ и PC₂C₁.
Биполярные координаты ^[3] характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B, а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы, поверхности, образуемые вращением дуг окружностей, а также полуплоскости, проходящие через ось O_z^[4].
Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью её удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований^[5]^[6].
Бицилиндрические координаты — система координат, которая образуется в том случае, если система биполярных координат на плоскости O_xy параллельно переносится вдоль оси O_z. В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров, оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы^[7].
Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса, и двух семейств перпендикулярных конусов, расположенных вдоль осей x и z^[8].
Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени, которая обыкновенно называется пространством Минковского. В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении, и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчёта, относительно которой она покоится.
Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол. Трехмерная модификация параболических координат строится путём вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка. Параболические координаты связаны определенным отношением с прямоугольными декартовыми^[9].
Проективные координаты существуют, согласно наименованию, в проективном пространстве П_n (К) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К, характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами^[10].
Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два её фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а, лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью^[11].
Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы^[12].
Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований^[13].
Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды, однополостные гиперболоиды, а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы

O_xyz симметричны друг другу^[14].

Переход из одной системы координат в другую[править | править код]

Декартовы и полярные[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

где u₀ — функция Хевисайда с u0(0)=0,{\displaystyle u_{0}(0)=0,} а sgn — функция signum. Здесь функции u₀ и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая возвращает правильный φ в необходимом квадранте, определённом координатами x и y.

Декартовы и цилиндрические[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

z=z.{\displaystyle z=z.\quad }

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

z=z.{\displaystyle z=z.\quad }

(dxdydz)=(rcos⁡θ−rsin⁡φ0rsin⁡θrcos⁡φ0001)⋅(drdφdz),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \theta &-r\sin \varphi &0\\r\sin \theta &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}

(drdφdz)=(xx2+y2yx2+y20−yx2+y2xx2+y20001)⋅(dxdydz).{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Декартовы и сферические[править | править код]

x=ρsin⁡θcos⁡φ,{\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }

y=ρsin⁡θsin⁡φ,{\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;\quad }

ρ=x2+y2+z2,{\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}

θ=arccos⁡zρ=arctg⁡x2+y2z,{\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y.{\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}

(dx

Угловое расстояние — Википедия

Материал из Википедии — свободной энциклопедии

В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.

Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.

Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).

Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.

Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.

Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).

Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — tan⁡(aD){\displaystyle \tan({\frac {a}{D}})}:

θ≈aD{\displaystyle \theta \approx {\dfrac {a}{D}}}

Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), α∈[0,2π]{\displaystyle \alpha \in [0,2\pi ]} и склонением (dec), δ∈[−π/2,π/2]{\displaystyle \delta \in [-\pi /2,\pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:

θ=cos−1⁡[sin⁡(δ1)sin⁡(δ2)+cos⁡(δ1)cos⁡(δ2)cos⁡(α1−α2)]{\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}

НИЗКИЕ ШИРОТЫ — это… Что такое НИЗКИЕ ШИРОТЫ?

НИЗКИЕ ШИРОТЫ

НИЗКИЕ ШИРОТЫ: условное название зоны на поверхности земного шара, расположенной между 40° с. ш. и той же широтой Южного полушария; общее название тропических и субтропических широт. Низкие широты характеризуются специфическими экологическими особенностями: по сравнению с высокими широтами, здесь наблюдается большее видовое разнообразие растительного и животного мира, большая устойчивость экосистем, меньшая флюктуация численности видовых популяций, более высокая биологическая продуктивность и др.

НИЗИННЫЙ ЛУГ
НИЗМЕННОСТЬ

Смотреть что такое «НИЗКИЕ ШИРОТЫ» в других словарях:

низкие широты — Условное название тропических и субтропических областей земного шара, расположенных примерно между 40° северной и южной широты или между тропиками Рака и Козерога … Словарь по географии
Климат — (греч. κλίμα, κλίματος означает наклон солнца, иначе сказать, полуденную высоту солнца). Древние географы делили Землю на климатические пояса в зависимости от этого явления и длины дня, принимая в расчет так называемые астрономические климаты,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Океаны* — Общее понятие. Под этим именем в физической географии подразумевают обширное пространство вод, разделяющих между собой материки. Классификация. До последнего времени в науке господствовало следующее разделение О., введенное в 1845 г. лондонским… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Океаны — Общее понятие. Под этим именем в физической географии подразумевают обширное пространство вод, разделяющих между собой материки. Классификация. До последнего времени в науке господствовало следующее разделение О., введенное в 1845 г. лондонским… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
КАРТА — уменьшенное обобщенное изображение поверхности Земли (или ее части) на плоскости. Человек создавал карты с древнейших времен, пытаясь наглядно представить взаимное расположение различных участков суши и морей. Собрание карт, обычно переплетенных… … Энциклопедия Кольера
Полярные страны Северного полушария* — Северный Ледовитый океан, в противоположность Южному, представляет совершенно средиземный характер. Он на значительном протяжении имеет естественные границы и только в трех местах непосредственно сливается с водами Атлантического и Тихого… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Полярные страны северного полушария — Северный Ледовитый океан, в противоположность южному, представляет совершенно средиземный характер. Он на значительном протяжении имеет естественные границы и только в трех местах непосредственно сливается с водами Атлантического и Тихого… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Лед — (физ.) твердое тело, образующееся из воды при понижении ее температуры до нуля и ниже. Переход воды в Л. есть физическое явление и совершается без изменения химического ее состава, но газы, растворенные в воде, при замерзании выделяются; соли… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Семейство Дельфиновые (Delphinidae) — Дельфиновые мелкие (1 10 м), преимущественно очень подвижные морские китообразные стройного сложения. У большинства дельфиновых имеется спинной плавник, расположенный близ середины тела. У хвостового плавника на заднем крае глубокая… … Биологическая энциклопедия
Субтропический хребет — Картина циркуляции воздуха на Земле. Зона типичного расположения cубтропичного хребта известна как конские широты. Субтропический хребет, или субтропический пояс высокого давления полоса высокого атмосферно … Википедия

Угловой размер — Википедия

Материал из Википедии — свободной энциклопедии

Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.

Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.

Если отрезок длиной D перпендикулярен линии наблюдения (более того, она является серединным его перпендикуляром) и находится на расстоянии L от наблюдателя, то точная формула для углового размера этого отрезка: 2arctg⁡D2L{\displaystyle 2\,\operatorname {arctg} {\frac {D}{2L}}}. Если размер тела D мал по сравнению с расстоянием от наблюдателя L, то угловой размер (в радианах) определяется отношением D/L, так как tg⁡α≈α{\displaystyle \operatorname {tg} \alpha \approx \alpha } для малых углов. При удалении тела от наблюдателя (увеличении L), угловой размер тела уменьшается.

Понятие углового размера очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.

Согласно геометрии предмет, удалённый от глаза на расстояние, в 57 раз большее его поперечника, должен представляться наблюдателю под углом почти в 1°.

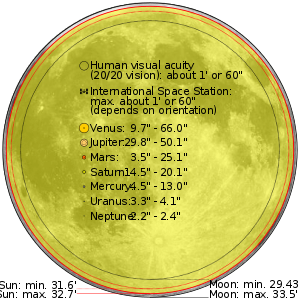$\operatorname {tg} \alpha \approx \alpha$

Сравнение угловых размеров Солнца, Луны и планет. Размеры приведены в угловых минутах (‘) и секундах («) Иллюстрация приведена не в масштабе: для того, чтобы получить точное представление о размерах, нужно рассматривать это изображение с расстояния, в 102.6 раз превышающего ширину кружка «Moon: max.». Например, если диаметр этого кружка на вашем мониторе составляет 10 см, то смотреть следует с расстояния 10,26 м.

Угловой размер астрономического объекта, видимый с Земли, обычно называется угловым диаметром или видимым диаметром. Вследствие удалённости всех объектов, угловые диаметры планет и звёзд очень малы и измеряются в угловых минутах (′) и секундах(″). Например, средний видимый диаметр Луны равен 31′05″ (вследствие эллиптичности лунной орбиты угловой размер изменяется от 29′20″ до 33′32″), или ≈0,5∘.{\displaystyle \approx 0{,}5^{\circ }.} Средний видимый диаметр Солнца — 31′59″ (изменяется от 31′31″ до 32′36″)^[1]. Видимые диаметры звёзд чрезвычайно малы и лишь у немногих достигают нескольких сотых долей секунды.

Длина высота широта – Как рассчитать протяженность материка 🚩 длина параллели в градусах 🚩 Гуманитарные науки