Градиент матпрофи: Градиент — Википедия – Как найти градиент функции в точке, примеры решений

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

1) функции одной переменной;

2) функции трёх переменных в нашем случае.

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x), соответствующее приращению аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, z отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче

.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;

2) произвольный вектор l с направляющими косинусами cosα, cosβ

, cosγ.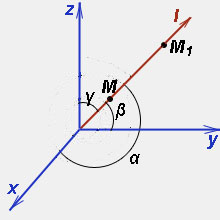

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

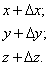
Величину отрезка MM1 можно обозначить .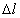

Функция u = f(M) при этом получит приращение

.

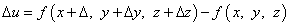Определение производной по направлению. Предел отношения 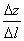при 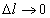, если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается 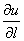, то есть

.

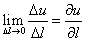
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

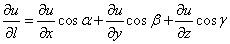Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Пример 1. Найти производную функции 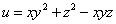в точке M0(1; 2; 3) по направлению вектора

.

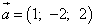
Решение. Найдём частные производные функции в точке M0:

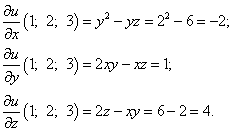
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

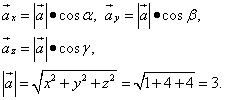
Следовательно,

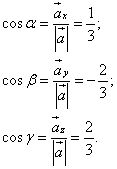
Теперь можем найти производную по направлению данной функции по её формуле:

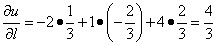
А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

---

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции 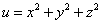в точке M0(1; 1; 1) по направлению вектора

.

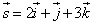
Решение. Найдём направляющие косинусы вектора

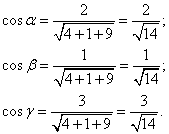
Найдём частные производные функции в точке M0:

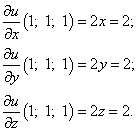
Следовательно, можем найти производную по направлению данной функции по её формуле:

.

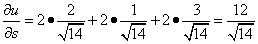Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке

M0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных 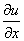, , 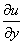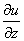этой функции в соответствующей точке:

.

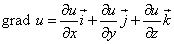То есть, должно получиться

представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

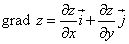Пример 4. Найти градиент функции 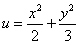в точке M0(2; 4;).

Решение. Найдём частные производные функции в точке M0:

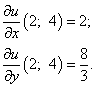
Следовательно, можем записать искомый градиент данной функции:

.

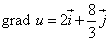Поделиться с друзьями

Производные

Функции нескольких переменных

Производная по направлению — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Производная.

В математическом анализе производная по направлению — одно из обобщений понятия производной на случай функции нескольких переменных. Производная по направлению показывает, как быстро функция изменяется при движении в данном направлении.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению

производной по направлению.

Рассмотрим функцию f(x1,…,xn){\displaystyle f(x_{1},\;\ldots ,\;x_{n})} от n{\displaystyle n} аргументов в окрестности точки x→0=(x10,…,xn0){\displaystyle {\vec {x}}{\,}^{0}=(x_{1}^{0},\;\ldots ,\;x_{n}^{0})}. Для любого единичного вектора e→=(e1,…,en){\displaystyle {\vec {e}}=(e_{1},\;\ldots ,\;e_{n})} определим производную функции f{\displaystyle f} в точке x→0{\displaystyle {\vec {x}}{\,}^{0}} по направлению e→{\displaystyle {\vec {e}}} следующим образом:

De→f(x→0)=∂f∂e=limh→0f(x→0+h⋅e→)−f(x→0)h{\displaystyle D_{\vec {e}}f({\vec {x}}{\,}^{0})={\frac {\partial f}{\partial e}}=\lim _{h\to 0}{\frac {f({\vec {x}}{\,}^{0}+h\cdot {\vec {e}})-f({\vec {x}}{\,}^{0})}{h}}}

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора e→{\displaystyle {\vec {e}}}.

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

Нормальная производная — производная по направлению нормали некоторой поверхности. Понятие нормальной производной особенно важно при решении краевых задач^[1] (см. пример в статье Задача Неймана). Если нормаль обозначить n{\displaystyle \mathbf {n} }, то нормальная производная ∂f∂n{\displaystyle {\frac {\partial f}{\partial n}}} для функции f даётся формулой:

∂f∂n=∇f(x)⋅n=∇nf(x)=∂f∂x⋅n=Df(x)[n].{\displaystyle {\frac {\partial f}{\partial \mathbf {n} }}=\nabla f(\mathbf {x} )\cdot \mathbf {n} =\nabla _{\mathbf {n} }{f}(\mathbf {x} )={\frac {\partial f}{\partial \mathbf {x} }}\cdot \mathbf {n} =Df(\mathbf {x} )[\mathbf {n} ].}

Для функции, заданной на плоскости, нормальная производная определяется как производная по направлению нормали некоторой кривой, лежащей в той же плоскости^[1].

Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:

∂f∂e=∇f⋅e→{\displaystyle {\frac {\partial f}{\partial e}}=\nabla f\cdot {\vec {e}}}

Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке.

1. ↑ ^{1 2} Нормальная производная // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 416. — 847 с.

МА. Производная по направлению. Градиент

Теоретический минимум

Переход от анализа функций одной переменной к анализу функций многих переменных — по крайней мере двух — приводит к значительному
усложнению теории. Помимо прочего теряется наглядность: если функция в общем случае задаёт кривую на плоскости, функция
— поверхность в пространстве, то функции большего числа аргументов уже не допускают подобной геометрической интерпретации.
С другой стороны теоретическое описание функций трёх и большего числа переменных уже принципиально не отличается от описания функций
двух переменных. Поэтому удобно вводить новые понятия именно на основе функций двух переменных, ещё позволяющих наглядно пояснять смысл
нововведений. Так поступим и при определении производной по направлению.

Напомним, что производная функции имеет простой геометрический смысл. Величина в точке равна угловому
коэффициенту касательной к графику этой функции в данной точке. Чем больше этот угловой коэффициент, тем больше угол, который составляет
касательная к графику с осью абсцисс. Чем больше этот угол, тем быстрее меняется функция в малой окрестности рассматриваемой точки. Таким образом,
производная позволяет определять скорость изменения функции.

Теперь обратимся к функции двух переменных. Она, как уже говорилось, определяет поверхность. Выберем точку этой поверхности и зададимся
вопросом о скорости изменения функции в этой точке. Здесь должно быть понятно, что вопрос сформулирован слишком грубо. Когда такой вопрос
ставился в отношении функции одной переменной, то там никаких проблем не было: аргумент мог изменяться только вдоль оси абсцисс. Если же у
функции хотя бы два аргумента, то её изменение определяется уже поведением двух аргументов. В связи с этим в вопрос о скорости изменения
функции следует ввести дополнение, задав направление, в котором будут изменяться её аргументы.

Начнём с частных случаев, а для примера возьмём известную из аналитической геометрии поверхность, которая задаётся уравнением

Поверхность представляет собой т.н. гиперболический параболоид (см. рис. 1).

Исследуем поведение функции в точке и её малой окрестности. Например, рассмотрим изменение этой функции
вдоль оси абсцисс. С геометрической точки зрения мы проводим плоскость ; с точки зрения формальной мы фиксируем один аргумент и
фактически переходим к функции одной переменной. А как исследовать функцию одной переменной известно — для этого существует понятие
производной. В терминологии анализа функций нескольких переменных производная функции по одной переменной при фиксированных остальных —
частная производная. Таким образом, в нашем примере скорость изменения функции в точке в направлении оси абсцисс
позволяет определить частная производная . Более того, мы можем расширить возможности этого инструмента.

Чтобы пояснить это, рассмотрим сечение параболоида плоскостью (см. рис. 2 — там сечение ограничивает вид поверхности сверху).
Это обычная парабола . Эта функция убывает при отрицательных значениях и возрастает при положительных значениях —
если рассматривается изменение функции вдоль оси абсцисс. Но мы можем рассмотреть и изменение функции в направлении, противоположном
направлению оси абсцисс — и тогда всё будет наоборот! При функция будет убывать, а при — возрастать. А частная производная
в данном случае даёт только правильную количественную характеристику скорости изменения функции, но неправильно определяет
характер монотонности. Это говорит о том, что всё-таки одной частной производной в данном случае недостаточно. Тем более что мы ведь
рассмотрели только удобный частный случай. Есть и второй удобный частный случай: рассмотреть изменение функции в направлении оси ординат —
там главную роль будет играть частная производная . Но как исследовать скорость изменения функции в произвольном направлении,
составляющем с осью абсцисс угол ?

Вот для этого и вводится понятие производной по направлению. Строгое определение таково:

Несложно понять его структуру: она полностью аналогична структуре производной функции одной переменной. Действительно, по своей сути
производная — отношение приращения функции к вызвавшему его приращению аргумента. В случае функции одной переменной рассматривается
одна-единственная возможность изменения аргумента — в направлении оси абсцисс. В анализе функций одной переменной это естественное
направление. Когда аргументов становится больше, например, два, то нужно задать изменение аргумента в произвольном направлении.
Именно так и устроены аргументы у первого слагаемого в числителе дроби. Там написано положение точки, смещённой от точки
по прямой, составляющей с осью абсцисс угол . Таким образом, в числителе дроби под пределом написано приращение функции при
смещении в направлении, составляющем с осью абсцисс угол , в знаменателе находится параметр, описывающий величину смещения
аргументов в этом направлении.

Как обычно, по определению считать производную неудобно, поэтому доказывается следующая простая формула:
.
Обратите внимание: если вычисляем производную в направлении оси абсцисс, то , и получается частная производная по переменной .
Если же мы хотим вычислять производную в противоположном направлении, то , и частная производная приобретает знак минус.
При дифференцировании вдоль оси ординат производная по этому направлению совпадает с частной производной по переменной (угол ).

Теперь можно и обобщить на случай трёх аргументов (а там уже будет ясно обобщение на любое число переменных). В трёхмерном случае направление
определяется направляющими косинусами — косинусами углов, которые направление составляет с осями координат.
.

Заметим, что введение направляющего вектора даёт возможность записать производную по направлению в виде
скалярного произведения:
,
где .
Этот вектор называется градиентом функции . Свойства градиента подробнее рассматриваются в векторном анализе. Здесь остановимся
только на его геометрическом смысле, столь важном, например, в физических приложениях. Смысл производной по направлению совпадает
со смыслом производной функции одного аргумента. Величина производной характеризует скорость изменения функции в данной точке
в данном направлении. В каком-то направлении функция может изменяться быстрее, в каком-то медленнее. В направлении самого быстрого
изменения функции производная будет самая большая по модулю. С другой стороны производная по направлению — скалярное произведение
градиента функции и направляющего вектора данного направления:
.
Наибольшего значения это произведение достигает, когда косинус в правой части становится равным единице. А это возможно при
совпадении направления вектора и градиента функции. Следовательно, направление градиента функции и направлении,
при дифференцировании вдоль которого производная наибольшая, совпадают. Иными словами, градиент направлен в сторону скорейшего
возрастания функции — это и есть его геометрический смысл.

Примеры.

Пример 1. Вычисление производной по направлению.
Найдём производную функции в точке в направлении, составляющем угол 60 градусов с осью абсцисс.

Направляющие косинусы в данном случае , частные производные
.
Таким образом,
.
В качестве несложного упражнения можно вычислить эту производную по определению.

Пример 2. Градиент.
Вычислим градиент модуля радиус-вектора точки, т.е. функции .
Фактически требуется вычислить три частные производные:
.
Заметим, что эту формулу можно записать короче:
.
Она часто используется при вычислениях в векторном анализе.

Пример 3. Геометрический смысл градиента.
Для разнообразия приведём пример из физики, с помощью которого хотелось бы показать, как важно для понимания физических законов
хорошо знать математику. Пример, в действительности, хрестоматийный — закон теплопроводности или закон Фурье. Закон выражает плотность
потока тепла (по модулю это количество теплоты, которое переносится через единичную площадку за единицу времени) через
градиент температуры:
,
где — константа (для изотропной среды), называемая коэффициентом теплопроводности.
Оставляя в стороне количественное соотношение, утверждаемое этим эмпирическим законом, отметим, что в законе чётко прописано направление
переноса тепла. Так как градиент направлен в сторону скорейшего возрастания функции, то градиент, взятый со знаком минус, показывает
направление скорейшего убывания функции. Следовательно, в законе Фурье заложено распространение тепла в направлении скорейшего
убывания температуры.

Векторный анализ — Википедия

Материал из Википедии — свободной энциклопедии

Ве́кторный ана́лиз — раздел математики, распространяющий методы математического анализа на векторы, как правило в двух- или трёхмерном пространстве.

Объектами приложения векторного анализа являются:

Наибольшее применение векторный анализ находит в физике и инженерии. Основные преимущества векторных методов перед традиционными координатными:

1. Компактность. Одно векторное уравнение объединяет несколько координатных, и его исследование чаще всего можно проводить непосредственно, не заменяя векторы на их координатную запись.
2. Инвариантность. Векторное уравнение не зависит от системы координат и без труда переводится в координатную запись в любой удобной системе координат.
3. Наглядность. Дифференциальные операторы векторного анализа и связывающие их соотношения обычно имеют простое и наглядное физическое истолкование.

Наиболее часто применяемые векторные операторы:

Приведём сводку практически важных теорем многомерного анализа в векторной записи.

Теорема	Запись	Пояснения
Теорема о градиенте	φ(q)−φ(p)=∫L∇φ⋅dr.{\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{L}\nabla \varphi \cdot d\mathbf {r} .}	Криволинейный интеграл от градиента скалярного поля равен разности значений поля в граничных точках кривой.
Теорема Грина	∮C⁡Ldx+Mdy=∬D(∂M∂x−∂L∂y)dA{\displaystyle \oint \limits _{C}L\,dx+M\,dy=\iint \limits _{D}\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\,dA}	Криволинейный интеграл по замкнутому плоскому контуру может быть преобразован в двойной интеграл по области, ограниченной контуром.
Теорема Стокса	∫Σ∇×F⋅dΣ=∮∂Σ⁡F⋅dr,{\displaystyle \int \limits _{\Sigma }\nabla \times \mathbf {F} \cdot d\mathbf {\Sigma } =\oint \limits _{\partial \Sigma }\mathbf {F} \cdot d\mathbf {r} ,}	Поверхностный интеграл от ротора векторного поля равен циркуляции по границе этой поверхности.
Теорема Остроградского — Гаусса	∭V(∇⋅F)dV=∬∂VF⋅dS,{\displaystyle \iiint \limits _{V}\left(\nabla \cdot \mathbf {F} \right)dV=\iint \limits _{\partial V}\mathbf {F} \cdot d\mathbf {S} ,}	Объёмный интеграл от дивергенции векторного поля равен потоку этого поля через граничную поверхность.

Первым векторы ввёл У. Гамильтон в связи с открытием в 1843 г. кватернионов (как их трёхмерную мнимую часть). В двух монографиях (1853, 1866 посмертно) Гамильтон ввёл понятие вектора и вектор-функции, описал дифференциальный оператор ∇{\displaystyle \nabla } («набла», 1846) и многие другие понятия векторного анализа. Он определил в качестве операций над новыми объектами скалярное и векторное произведения, которые для кватернионов получались чисто алгебраически (при обычном их умножении). Гамильтон ввёл также понятия коллинеарности и компланарности векторов, ориентации векторной тройки и др.

Компактность и инвариантность векторной символики, использованной в первых трудах Максвелла (1873), заинтересовали физиков; вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному исчислению современный вид. Примечательно, что уже в работах Максвелла кватернионная терминология почти отсутствует, фактически заменённая на чисто векторную. Термин «векторный анализ» предложил Гиббс (1879) в своём курсе лекций.

• Александрова Н. В. Формирование основных понятий векторного исчисления. // Историко-математические исследования. — М.: Наука, 1982. — № 26. — С. 205-234.
• Борисенко А. И., Тарапов И. Е. Векторный анализ и начала тензорного исчисления. М.: Высшая школа, 1966, 251 с.
• Краснов М. Л., Кисилев А. И., Макаренко Г. И. Векторный анализ. Наука, 1978, 160 с. (2-ое изд. УРСС, 2002)
• Кумпяк Д. Е. Векторный и тензорный анализ. Учебное пособие. Тверь: Тверской гос. университет, 2007, 158 с.
• Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. М.: Физматлит, 1963, 411 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, том III. — М.: Наука, 1966.

Градиент — это… Что такое Градиент?

Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.

Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве.

Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным.

Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.

Стандартные обозначения:

или, с использованием оператора набла,

— вместо может быть любое скалярное поле, обозначенное любой буквой, например  — обозначения градиента поля V.

Определение

Для случая трёхмерного пространства градиентом скалярной функции координат , , называется векторная функция с компонентами

, , .

Или, использовав для единичных векторов по осям прямоугольных декартовых координат :

Если  — функция переменных , то её градиентом называется -мерный вектор

компоненты которого равны частным производным по всем её аргументам.

• Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.
• Оператором градиента (обозначаемым обычно, как говорилось выше, или ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто «градиентом».

Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена , то есть линейную (в случае общего положения она же главная) часть изменения при смещении на . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку  — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

или, опуская по правилу Эйнштейна знак суммы,

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Пример

Например, градиент функции будет представлять собой:

В физике

В различных отраслях физики используется понятие градиента различных физических полей.

Например, напряженность электростатического поля есть минус градиент электрического потенциала, напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Сила в классической механике есть минус градиент потенциальной энергии.

В естественных науках

Понятие градиента находит применение не только в физике, но и в смежных и даже сравнительно далеких от физики науках (иногда это применение носит количественный, а иногда и просто качественный характер).

Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по какому-то направлению температуры среды и т. д.

Градиент таких величин может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз.

Геометрический смысл

Рассмотрим семейство линий уровня функции :

Нетрудно показать, что градиент функции в точке перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности , то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъема в данной точке.

Связь с производной по направлению

Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции по направлению равняется скалярному произведению градиента на единичный вектор :

Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.

Градиент в ортогональных криволинейных координатах

где  — коэффициенты Ламе.

Полярные координаты (на плоскости)

Коэффициенты Ламе:

Отсюда:

Цилиндрические координаты

Коэффициенты Ламе:

Отсюда:

Сферические координаты

Коэффициенты Ламе:

.

Отсюда:

См. также

Литература

1. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Учебное пособие для физико-математических специальностей университетов, 1986. стр.30