Размеры катеров
От размеров судна (или, правильнее говоря, размерений) – длины, ширины, осадки и высоты борта – в значительной степени зависят его мореходные и эксплуатационные качества.
Оптимальные размерения строящихся катеров устанавливаются с учетом широкого спектра различных показателей:
- вместимости,
- остойчивости,
- ходкости,
- управляемости,
- устойчивости на курсе,
- парусности,
- мощности двигателя,
- прочностных характеристик корпуса и др.
Хотя основной областью применения термина «размерения» является судостроение, его используют специалисты других отраслей. Например, в автомобилестроении применительно к размерам кузовов автомобилей, а в строительстве – к металлическим и деревянным каркасам.
В существительном «размерение» акцентировано звучит активное начало. Размерение – не просто констатация определенной величины, а результат предварительного расчета, запланированного целенаправленного действия.
Согласно ГОСТ 1062-80 «Размерения надводных кораблей и судов главные. Термины, определения и буквенные обозначения», термином «главные размерения судна» обозначается совокупность конструктивных, расчетных, наибольших и габаритных линейных размеров судна.
Для судов (в т. ч. катеров) неводоизмещающего типа (глиссирующих, на подводных крыльях, на воздушной подушке, экранопланов) – определения главных размерений относят к плаванию в водоизмещающем режиме. Определения главных размерений для многокорпусных судов (исключая габаритные) относятся к каждому корпусу в отдельности.
Размерения (размеры катеров) имеют и вполне прикладное значение. Так, в Разъяснении управления ГИМС (Государственной инспекции по маломерным судам) МЧС России в связи с вступлением в силу Федерального закона от 23.04.2012 № 36-Ф3 «О внесении изменений в отдельные законодательные акты Российской Федерации в части определения понятия маломерного судна» указывается: «В качестве длины судна для целей государственной регистрации согласно Закону применять определение «наибольшая длина судна» данное в ГОСТ 1062-80 «Размерения надводных кораблей и судов главные термины, определения и буквенные обозначения»».
Для судна с подвесным мотором еще одним важным размером является высота транца. Если он слишком высокий для используемого мотора, то работающий близко к водной поверхности винт будет захватывать воздух. В противном случае, нижняя часть двигателя будет создавать дополнительное сопротивление потоку воды.
Если главные размерения – длина (L), ширина (В), высота борта (Н) и осадка (Т) – определяют только размеры катера, то их соотношения L/B, В/Т, H/T, L/H, L/T и B/H отражают непосредственное влияние его геометрических параметров на мореходные качества и прочностные характеристики.
Отношение длины к ширине по ватерлинии (L/B) характеризует ходкость (способность катера развивать заданную скорость при определенной затрате мощности главного судового двигателя). Чем большее численное значение имеет отношение L/B, тем быстроходнее судно водоизмещающего типа. Чем L/B меньше, тем оно (при одинаковой длине) остойчивее.
Неудивительно, что гоночные катера имеют вытянутую сигарообразную форму. И не только гоночные. Во времена быстроходных клиперов к их ширине относились очень «экономно». Так, у одного из самых быстрых кораблей своего времени Cutty Sark (построен в 1869 г.), использовавшегося для перевозки на Британские острова чая из Китая и шерсти из Австралии, длина превышала ширину более, чем в 6 раз.
И не только гоночные. Во времена быстроходных клиперов к их ширине относились очень «экономно». Так, у одного из самых быстрых кораблей своего времени Cutty Sark (построен в 1869 г.), использовавшегося для перевозки на Британские острова чая из Китая и шерсти из Австралии, длина превышала ширину более, чем в 6 раз.
От отношения L/B зависит управляемость катером. Его увеличение означает улучшение устойчивости на курсе при снижении поворотливости. Короткий корпус позволяет выиграть в весе, но управлять таким катером станет труднее.
Отношение ширины по конструктивной ватерлинии к осадке (В/Т) характеризует ходкость и остойчивость катера. Чем В/Т больше, тем он остойчивее. С уменьшением этого отношения увеличивается устойчивость на курсе, однако снижается способность сохранять скорость на волнении. Узкий катер с большой осадкой имеет меньшую остойчивость, чем широкий с малой.
Отношение полной высоты борта к осадке (Н/Т) характеризует запас плавучести катера и влияет на его остойчивость, непотопляемость и вместимость. Чем оно больше, тем большую нагрузку способен принять катер без опасности заливания волной.
Чем оно больше, тем большую нагрузку способен принять катер без опасности заливания волной.
С увеличением отношения H/T растет парусность, от которой существенно зависит кренящий момент, возникающий при действии на катер штормовых волн и порывов ветра.
Отношение наибольшей длины к высоте борта (L/H) характеризует прочность и жесткость корпуса (они повышаются с уменьшением этого отношения), а значит, способность катера переносить нагрузки от волнения. Чем меньше отношение длины к осадке (L/T), тем катер маневреннее.
О современных тенденциях в установлении размерений катеров (размеров катеров) можно судить на примере моделей, производимых компанией «Сильвер» из Санкт-Петербурга.
Самый короткий катер имеет длину 4,5 м, самый длинный катер – более 10 м. Причем более ¾ от общего числа моделей попадает в диапазон 5-8 м, а почти половина в еще более узкий – 6-7 м.
Ширина катеров Silver находится в пределах 181-278 см.
У большинства моделей отношение длины к ширине (L/B) находится в промежутке от 2,4 до 3 и только у нескольких катеров превышает 3 (NorthSilver PRO 920 – 3,7 NorthSilver 730 Star Cabin ST – 3,12).
Отношение ширины к осадке (В/Т) составляет от 5,5 до 8, высоты борта к осадке (H/T) – от 1,8 до 2,40, наибольшей длины к высоте борта (Lнб/Н) – от 7 до 11.
Значение размеров катера не исчерпывается конструкторской документацией. Во многом определяя его безопасность, надежность и функциональные свойства (например, удобство размещения грузов и пассажиров), размерения учитываются не только при проектировании и изготовлении, но и в процессе эксплуатации катеров: при выборе района плавания (особенно в таких «проблемных» местах как шлюзы, каналы, пороги) и пунктов швартовки, организации транспортирования судна к месту хранения и т. д.
Длина судна по конструктивной ватерлинии (Lквл) – расстояние между точками пересечения носовой и кормовой частей конструктивной ватерлинии с диаметральной плоскостью судна.
Длина судна по расчетной ватерлинии (Lвл) – расстояние между точками пересечения носовой и кормовой частей расчетной ватерлинии с диаметральной плоскостью судна.
Наибольшая длина судна (Lнб) – расстояние, измеренное в горизонтальной плоскости между крайними точками теоретической поверхности корпуса судна в носовой и кормовой оконечностях.
Габаритная длина судна (Lгб) – расстояние, измеренное в горизонтальной плоскости между крайними точками носовой и кормовой оконечностей корпуса судна с учетом постоянно выступающих частей.
Ширина судна по конструктивной ватерлинии (Вквл) – наибольшая ширина конструктивной ватерлинии судна.
Ширина судна по расчетной ватерлинии (Ввл) – наибольшая ширина расчетной ватерлинии судна.
Наибольшая ширина судна (Внб) – наибольшее расстояние, измеренное перпендикулярно диаметральной плоскости между крайними точками теоретической поверхности корпуса судна.
Габаритная ширина судна (Вгб) – наибольшее расстояние, измеренное перпендикулярно диаметральной плоскости между крайними точками корпуса судна с учетом постоянно выступающих частей.
Теоретическая поверхность корпуса судна – поверхность судна, проходящая по наружным кромкам днищевого, бортового и палубного набора основного корпуса, надстроек, фальшборта и козырька.
Высота борта судна (Hвп) — вертикальное расстояние, измеренное в плоскости мидель-шпангоута от основной плоскости до бортовой линии верхней палубы судна. Под бортовой линией понимается линия пересечения поверхности борта (без учета обшивки) и верхней палубы (без учета толщины настила).
Высота надводного борта (F) — разность между высотой борта и осадкой: F = H-Т.
Осадка судна по конструктивную ватерлинию (Тквл) – вертикальное расстояние, измеренное в плоскости мидель-шпангоута от основной плоскости до плоскости конструктивной ватерлинии судна.
Стол лабораторный усиленный длиной L=1800 мм, высотой H=900 мм, глубиной B=750 мм «ЕвроЭксперт»
Главная \ Каталог \Лабораторная мебель «Эксперт» \Лабораторная мебель серии «ЕвроЭксперт» \Лабораторные столы «ЕвроЭксперт» \ Стол лабораторный усиленный длиной L=1800 мм, высотой H=900 мм, глубиной B=750 мм «ЕвроЭксперт»
Особенности
- в основе стола – прочный металлический каркас с порошковым покрытием, обеспечивающий надежность конструкции;
- комплектуется дополнительным ребром жёсткости для большей надёжности стола;
- лицевой съемный экран для быстрого доступа к коммуникациям;
- допустимая распределенная нагрузка на рабочую поверхность до 500 кг;
- регулируемые опоры для компенсации неровностей пола.

| Характеристики | Значения | |||||
|---|---|---|---|---|---|---|
| Серия | ЕвроЭксперт | |||||
| Артикул | 21-14, 61-14 | |||||
| Габаритные размеры, мм: | ||||||
| длина | 1800 | |||||
| глубина | 750 | |||||
| высота | 900 | |||||
| Цвет/Текстура | Светло-серый, серый/ матовая в два цвета | |||||
| Материал | Металл | |||||
| Рабочая поверхность: | ламинат высокого давления | |||||
| керамогранит | ||||||
| дюркон | ||||||
| дюркон с бортиком | ||||||
| лабгрейд | ||||||
| искусственный кварцевый камень | ||||||
| бесшовный керамогранит | ||||||
| монолитная керамика | ||||||
| Комплектация: | для работы стоя | |||||
| для работы сидя | ||||||
| Дополнительно: | мобильная тумба | |||||
|
установка сервисной или титровальной надстройки |
||||||
| установка электрического блока с розетками | ||||||
|
подвод/слив воды, подвод газовых коммуникаций |
||||||
Специализированный стол лабораторный усиленный длиной L=1800 мм, высотой H=900 мм, глубиной B=750 мм «ЕвроЭксперт» поставленый компанией Лабор пользуется популярностью на пространстве СНГ. За время эффективной работы нашей компании, данные изделия нашли своё законное место в лабораториях предприятий производственной и социальной сферы, а также ряда других отраслей промышленности. Стол полностью соответствует ГОСТ 16371-2014, доказательством чему являются выданные сертификаты. Кроме того, вся специализированная продукция нашей компании отвечает европейскому стандарту ISO 9001:2015, что также подтверждено сертификатом.
За время эффективной работы нашей компании, данные изделия нашли своё законное место в лабораториях предприятий производственной и социальной сферы, а также ряда других отраслей промышленности. Стол полностью соответствует ГОСТ 16371-2014, доказательством чему являются выданные сертификаты. Кроме того, вся специализированная продукция нашей компании отвечает европейскому стандарту ISO 9001:2015, что также подтверждено сертификатом.
Стол лабораторный усиленный длиной L=1800 мм, высотой H=900 мм, глубиной B=750 мм отличает надёжная конструкция, созданная на базе металлического каркаса, окрашенного порошковой эпоксидной краской светло-серого цвета. Для усиления прочностных характеристик столы оборудуются дополнительным ребром жёсткости. Для свободного доступа к коммуникациям стол обеспечивается открывающимися экранами. В комплект стола включены различные типы поверхностей. В целом, столы лабораторные усиленные — это незаменимые изделия для организаций, в которых эксплуатируется тяжёлое и громоздкое оборудование.
Закажите стол лабораторный усиленный длиной L=1800 мм, высотой H=900 мм, глубиной B=750 мм от Торгового дома «Лабор» по оптимальной цене!
ВАМ НЕОБХОДИМА ПОМОЩЬ В ПОДБОРЕ МЕБЕЛИ?
Позвоните нам или оставьте свой номер для звонка менеджера
8 (812) 509-60-85
Согласен на обработку персональных данных
Рекомендуем посмотреть
Стол лабораторный для приборов длиной L=1500 мм, высотой H=1050 мм, глубиной B=750 мм «ЕвроЭксперт»
Стол лабораторный усиленный длиной L=1200 мм, высотой H=900 мм, глубиной B=750 мм «ЕвроЭксперт»
Надстройка лабораторная титровальная высотой H=900-1000 мм «ЕвроЭксперт»
Стол лабораторный физический длиной L=1200 мм, высотой H=900 мм, глубиной B=750 мм «ЕвроЭксперт»
Стол лабораторный усиленный длиной L=900 мм, высотой H=750 мм, глубиной B=620 мм «ЕвроЭксперт»
Стол лабораторный химический с мойкой длиной L=1200 мм, высотой H=900 мм, глубиной B=620 мм «ЕвроЭксперт»
Диафрагмы жесткости
Назад
Диафрагмы жесткости используются для укрепления каркасов зданий и сооружений и обеспечить их безопасной эксплуатации. Диафрагмы жесткости обеспечивают пространственную жесткость многоэтажных зданий, которые связывают между собой колонны и панели.
Диафрагмы жесткости обеспечивают пространственную жесткость многоэтажных зданий, которые связывают между собой колонны и панели.
Несущая способность диафрагм жесткости обеспечивается прочностью бетона, однако для повышения надежности конструкции из армируются горизонтальными и вертикальными стержнями у противоположных граней
Диафрагмы предназначены:
- для передачи давления фундаменту,
- для защиты сооружения от повреждений при сильном ветре,
- для связи остальных элементов и блоков в единое целое.
Обозначение диафрагм жесткости:
- Д – сплошная;
- ДП – с проемом;
- 1Д – сплошная с одной полкой;
- 2Д – сплошная с двумя полками:
- 1ДП (2ДП) – с одной (с двумя) полками с проемами, расположенными посередине.
Длина, L: 2560
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 3,35
Заказать
2560
140
3270
3,35
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3270
Масса изделия,т. : 3,78
: 3,78
Заказать
2560
140
3270
3,78
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 2,38
Заказать
2560
140
3270
2,38
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 2,93
Заказать
2560
140
3270
2,93
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 3,63
Заказать
2560
140
3570
3,63
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 4,05
Заказать
2560
140
3570
4,05
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3570
Масса изделия,т. : 2,63
: 2,63
Заказать
2560
140
3570
2,63
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 3,15
Заказать
2560
140
3570
3,15
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 4,18
Заказать
2560
140
4170
4,18
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 4,6
Заказать
2560
140
4170
4,6
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 3,1
Заказать
2560
140
4170
3,1
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 4170
Масса изделия,т. : 3,6
: 3,6
Заказать
2560
140
4170
3,6
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 3,9
Заказать
2980
140
3270
3,9
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 4,4
Заказать
2980
140
3270
4,4
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 2,88
Заказать
2980
140
3270
2,88
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3270
Масса изделия,т.: 3,38
Заказать
2980
140
3270
3,38
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3570
Масса изделия,т. : 4,23
: 4,23
Заказать
2980
140
3570
4,23
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 4,73
Заказать
2980
140
3570
4,73
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 3,7
Заказать
2980
140
3570
3,7
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 3570
Масса изделия,т.: 3,7
Заказать
2980
140
3570
3,7
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 4,85
Заказать
2980
140
4170
4,85
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 4170
Масса изделия,т. : 5,35
: 5,35
Заказать
2980
140
4170
5,35
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 3,83
Заказать
2980
140
4170
3,83
Заказать
Длина, L: 2980
Ширина, b: 140
Высота, h: 4170
Масса изделия,т.: 4,33
Заказать
2980
140
4170
4,33
Заказать
Длина, L: 2070
Ширина, b: 140
Высота, h: 3710
Масса изделия,т.: 2.57
Заказать
2070
140
3710
2.57
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 2810
Масса изделия,т.: 2.47
Заказать
2560
140
2810
2. 47
47
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3710
Масса изделия,т.: 3.29
Заказать
2560
140
3710
3.29
Заказать
Длина, L: 2660
Ширина, b: 120
Высота, h: 3710
Масса изделия,т.: 2.9
Заказать
2660
120
3710
2.9
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 2810
Масса изделия,т.: 2.68
Заказать
2770
140
2810
2.68
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 3280
Масса изделия,т.: 3.12
Заказать
2770
140
3280
3.12
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 3710
Масса изделия,т. : 3.34
: 3.34
Заказать
2770
140
3710
3.34
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 4180
Масса изделия,т.: 3.96
Заказать
2770
140
4180
3.96
Заказать
Длина, L: 2820
Ширина, b: 120
Высота, h: 3280
Масса изделия,т.: 2.75
Заказать
2820
120
3280
2.75
Заказать
Длина, L: 2820
Ширина, b: 120
Высота, h: 4180
Масса изделия,т.: 3.52
Заказать
2820
120
4180
3.52
Заказать
Длина, L: 2980
Ширина, b: 120
Высота, h: 3710
Масса изделия,т.: 3.25
Заказать
2980
120
3710
3. 25
25
Заказать
Длина, L: 4060
Ширина, b: 140
Высота, h: 2810
Масса изделия,т.: 3.94
Заказать
4060
140
2810
3.94
Заказать
Длина, L: 2020
Ширина, b: 140
Высота, h: 3230
Масса изделия,т.: 2.23
Заказать
2020
140
3230
2.23
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 2330
Масса изделия,т.: 2.09
Заказать
2560
140
2330
2.09
Заказать
Длина, L: 2560
Ширина, b: 140
Высота, h: 3230
Масса изделия,т.: 2.85
Заказать
2560
140
3230
2.85
Заказать
Длина, L: 2660
Ширина, b: 120
Высота, h: 1430
Масса изделия,т. : 1.12
: 1.12
Заказать
2660
120
1430
1.12
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 2330
Масса изделия,т.: 2.23
Заказать
2770
140
2330
2.23
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 2800
Масса изделия,т.: 2.65
Заказать
2770
140
2800
2.65
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 3230
Масса изделия,т.: 3.1
Заказать
2770
140
3230
3.1
Заказать
Длина, L: 2770
Ширина, b: 140
Высота, h: 3700
Масса изделия,т.: 3.53
Заказать
2770
140
3700
3. 53
53
Заказать
Длина, L: 4060
Ширина, b: 140
Высота, h: 2330
Масса изделия,т.: 3.25
Заказать
4060
140
2330
3.25
Заказать
Длина, L: 5660
Ширина, b: 120
Высота, h: 1430
Масса изделия,т.: 2.38
Заказать
5660
120
1430
2.38
Заказать
Длина, L: 5660
Ширина, b: 120
Высота, h: 1930
Масса изделия,т.: 3.25
Заказать
5660
120
1930
3.25
Заказать
1.4 Размерный анализ | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Находить размерности математического выражения, включающего физические величины.

- Определить, является ли уравнение, включающее физические величины, размерно-согласованным.
Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. (Рисунок) перечислены основные величины и символы, используемые для их измерения. Например, говорят, что измерение длины имеет размерность L или L 1 , измерение массы имеет размерность M или M 1 , а измерение времени имеет размерность T или T 1 . Как и единицы, измерения подчиняются правилам алгебры. Таким образом, площадь является произведением двух длин и поэтому имеет размерность L 2 , или длину в квадрате. Точно так же объем является произведением трех длин и имеет размерность L 3 , или длину в кубе. Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
Физики часто называют безразмерные величины чистыми числами .
| Базовое количество | Символ размера |
|---|---|
| Длина | л |
| Масса | М |
| Время | Т |
| Текущий | я |
| Термодинамическая температура | Θ |
| Количество вещества | Н |
| Сила света | Дж |
Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Важность понятия размерности проистекает из того факта, что любое математическое уравнение, связывающее физические величины, должно быть размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:
- Каждый член выражения должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
- Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными.
 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь вспомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2} [/латекс] и [латекс] 2\pi r. [/latex] Одно выражение — это длина окружности круга радиусом r , а другое — его площадь. Но что есть что?
Стратегия
Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
[латекс] [2\pi r]=[2]·[\pi ]·[r]=1·1·\text {L}=\text{L,} [/latex]
, так как константы [latex] 2 [/latex] и [latex] \pi [/latex] безразмерны, а радиус [latex] r [/latex ] — это длина. Мы видим, что [латекс] 2\pi r [/латекс] имеет размерность длины, что означает, что он никак не может быть площадью.
Мы исключаем [латекс] 2\pi r [/латекс], потому что его размеры не соответствуют площади. Мы видим, что [латекс] \pi {r}^{2} [/латекс] согласуется по размерам с областью, поэтому, если нам нужно выбирать между этими двумя выражениями, [латекс] \пи {г}^{2} [/latex] — это то, что нужно выбрать. {2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
{2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
Стратегия
В соответствии с определением размерной согласованности нам необходимо проверить, что каждый член данного уравнения имеет те же размерности, что и другие члены этого уравнения, и что аргументы любых стандартных математических функций безразмерны.
Решение
- В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})]=1.\hfill \end{массив} [/latex]
Два термина имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».
Значение
Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Проверьте свое понимание
Соответствует ли размерность уравнения v = at ?
Показать решение
Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :
[латекс] [ \frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]
[/latex]
Аналогично, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла v по отношению к t — это просто размерность v , умноженная на размерность t :
[латекс] [\int vdt]=[v]·[t]. [/latex]
По тем же рассуждениям аналогичные правила справедливы для единиц физических величин, полученных из других величин путем интегрирования или дифференцирования.
Резюме
- Размерность физической величины — это просто выражение основных величин, из которых она получена.
- Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2}; [/latex] (c) [latex] v=s\text{/}t; [/latex] (d) [latex] a=v\text{/}t. [/latex]
Показать решение
Рассмотрим физические величины [латекс] m, [/латекс] [латекс] s, [/латекс] [латекс] v, [/латекс] [латекс] а, [/латекс] и [латекс] t [/латекс ] с размерами [ м ] = M, [ s ] = L, [ v ] = LT –1 , [ a ] = LT –2 , и [ 2 t 90 ] T.
 Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .
Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .Предположим, что количество [латекс] s [/латекс] — это длина, а количество [латекс] t [/латекс] — это время. Предположим, что количества [латекс] v [/латекс] и [латекс] а [/латекс] определены как v = ds / dt и a = dv / dt . а) Какова размерность числа 9?{–3}, [/latex] и [t] = T. (a) Какова размерность [latex] \int \rho dV? [/latex] (b) Каков размер dV / dt ? в) Каков размер [латекс] \rho (dV\text{/}dt)? [/latex]
Формула длины дуги говорит, что длина [латекс] s [/латекс] дуги, опирающейся на угол [латекс] Ɵ [/латекс] в окружности радиусом [латекс] r [/латекс], определяется выражением уравнение [латекс] s=rƟ.
 [/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числом
[/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числомРазмеры — литые пирорезервуары
Стандартные размеры резервуаров с плоским дном (дюймы)
Также доступны нестандартные размерыРезервуар № . Длина (Д) Ширина (Ш) Высота (В)† 7467 6,50 5,50 6,00 7545 7,60 5,60 10.  00
007478 7,50 6,50 7,81 7479 7,50 7,25 8,81 7457 7,75 7,75 9,81 7445 9,00 7,50 9,00 7466 11,50 7,50 7,81 7498 12.00 11.00 11,69 7484 16.  00
008.00 9,81 7528 16,87 9,50 11.00 7526 17,77 10,65 12.00 7530 21,50 11,50 12,69
ТИПОВЫЕ РАЗМЕРЫ, PyroTank — наклонное дно
Стандартные размеры резервуара с наклонным дном (дюймы)
Также доступны размеры по индивидуальному заказуНомер резервуара Длина (Д) Ширина (Ш) Высота (В)† 7534-СБ 14.  00
0010.00 8,20/8,95 7526-СБ 17,70 10,65 12,325/12,70 ТИПОВЫЕ РАЗМЕРЫ PyroTank (показан бак с мешалкой)
Стандартные размеры бака Stirwell (в дюймах)
Длина (Д) Ширина (Ш) Высота (В)† 7458-SW 7,75 7,75 9,81 7496-SW 9,87 8,62 11.00 7472-SW 11,50 7,50 7,81 7474-Ш 13,50 7,50 8,81 7484-SW 16. 00 8,00 9,81 7496-SW 9,87 8,62 11.00 7498-SW 12.00 11.00 11,69
00 8,00 9,81 7496-SW 9,87 8,62 11.00 7498-SW 12.00 11.00 11,69Наборы стандартных фланцев (дюймы)
(поставляются от 4 до 6 шт.)Деталь № Длина (Д) Ширина (Ш) Толщина (Т) 7167-* по необходимости 1,00 .  190
190*Укажите номер резервуара при заказе фланца, например, 7167-7467
Стандартные фланцевые детали (дюймы)
Деталь № Длина (Д) Ширина (Ш) Высота (В)† 7167-11 11 1,00 0,190 7167-12 12 1,00 0,190 7167-13 13 1,00 0,190 7167-14 14 1,00 0,190 7167-15 15 1,00 0,190 7167-16 16 1,00 0,190
† Указанные размеры являются СТАНДАРТНЫМИ. Другие высоты доступны по запросу. Верхняя кромка стандартных резервуаров поставляется только в черновом варианте. Возможна огневая полировка за дополнительную плату.
Другие высоты доступны по запросу. Верхняя кромка стандартных резервуаров поставляется только в черновом варианте. Возможна огневая полировка за дополнительную плату.
†† Зависит от типа вафельной кассеты.
* Бак имеет наклон дна в сторону емкости для перемешивания.
** Увеличенный радиус угла и радиуса дна этих резервуаров.Copyright © 2010, Pyromatics Corp.
9321 Pineneedle Drive Mentor, Ohio 44060 (440) 352-3500Mathway | Популярные проблемы
9(1/2) 92-4*-1+2 921 Найдите том сфера (5) 2 Найти площадь круг (5) 3 Найдите площадь поверхности сфера (5) 4 Найти площадь круг (7) 5 Найти площадь круг (2) 6 Найти площадь круг (4) 7 Найти площадь круг (6) 8 Найдите том сфера (4) 11 Найти простую факторизацию 741 12 Найдите том сфера (3) 13 Оценка 3 квадратный корень из 8*3 квадратный корень из 10 14 Найти площадь круг (10) 15 Найти площадь круг (8) 16 Найдите площадь поверхности сфера (6) 17 Найти простую факторизацию 1162 18 Найти площадь круг (1) 19 Найдите окружность круг (5) 20 Найдите том сфера (2) 21 Найдите том сфера (6) 22 Найдите площадь поверхности сфера (4) 23 Найдите том сфера (7) 24 Оценка квадратный корень из -121 25 Найти простую факторизацию 513 26 Оценка квадратный корень из 3/16* квадратный корень из 3/9 27 Найдите том коробка (2)(2)(2) 28 Найдите окружность круг (6) 29 Найдите окружность круг (3) 30 Найдите площадь поверхности сфера (2) 31 Оценка 2 1/2÷22000000 32 Найдите Том коробка (5)(5)(5) 33 Найдите том коробка (10)(10)(10) 34 Найдите окружность круг (4) 35 Преобразование в проценты 1,7 36 Оценка (5/6)÷(4/1) 37 Оценка 3/5+3/5 38 Оценка ф(-2) 92 40 Найти площадь круг (12) 41 Найдите том коробка (3)(3)(3) 42 Найдите том коробка (4)(4)(4) 45 Найти простую факторизацию 228 46 Оценка 0+0 47 Найти площадь круг (9) 48 Найдите окружность круг (8) 49 Найдите окружность круг (7) 50 Найдите том сфера (10) 51 Найдите площадь поверхности сфера (10) 52 Найдите площадь поверхности сфера (7) 53 Определить, является простым или составным 5 60 Преобразование в упрощенную дробь 2 1/4 61 Найдите площадь поверхности сфера (12) 62 Найдите том сфера (1) 63 Найдите окружность круг (2) 64 Найдите том коробка (12)(12)(12) 65 Добавить 2+2= 66 Найдите площадь поверхности коробка (3)(3)(3) 67 Оценка корень пятой степени из 6* корень шестой из 7 68 Оценка 7/40+17/50 69 Найти простую факторизацию 1617 70 Оценка 27-(квадратный корень из 89)/32 71 Оценка 9÷4 72 Оценка 92 74 Оценка 1-(1-15/16) 75 Преобразование в упрощенную дробь 8 76 Оценка 656-521 9-2 79 Оценка 4-(6)/-5 80 Оценка 3-3*6+2 81 Найдите площадь поверхности коробка (5)(5)(5) 82 Найдите площадь поверхности сфера (8) 83 Найти площадь круг (14) 84 Преобразование в десятичное число 5 ноября 85 9-2 88 Оценка 1/2*3*9 89 Оценка 4/4-17/-4 90 Оценка 11. 

 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных. Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .
Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr . [/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числом
[/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числом 00
00 00
00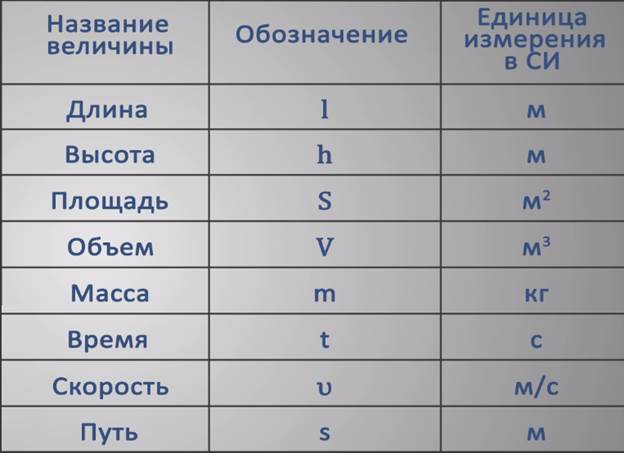 00
00 00 8,00 9,81 7496-SW 9,87 8,62 11.00 7498-SW 12.00 11.00 11,69
00 8,00 9,81 7496-SW 9,87 8,62 11.00 7498-SW 12.00 11.00 11,69 190
190 Другие высоты доступны по запросу. Верхняя кромка стандартных резервуаров поставляется только в черновом варианте. Возможна огневая полировка за дополнительную плату.
Другие высоты доступны по запросу. Верхняя кромка стандартных резервуаров поставляется только в черновом варианте. Возможна огневая полировка за дополнительную плату.