Построение овала — Чертежик
Рассмотрим построение овала двумя методами: окружности и параллелограмма.
Воспользуемся методом окружности.
1.) Начинаем чертить с построения осей.
2.) Чертим окружность
3.) Чертим дуги ЕА и BD радиусом ЕС
4.) Чертим дуги ED и AB радиусом FB
Применим метод параллелограмма.
1.) Начинаем с построения осевых линий
2.) Чертим линии параллельные осевым линиям. Где d — диаметр окружности.
3.) Строим дуги HB и DF радиусом HE4.) Продолжаем с черчения дуги BD радиуса MB и дуги FH радиусом PH
Применение построения овала на чертежах вы можете посмотреть здесь
Навигация по записям
Как нарисовать Овал правильно карандашом шаг за шагом?
В данном уроке вы найдете поэтапную схему рисования, состоящую из 9 шагов, посвященную тому, как нарисовать Овал правильно.
Шаг 1. Рисуем вертикаль и горизонталь, которые пересекаются под прямым углов в 90 градусов. В верхней части вертикали ставим засечку и измеряем расстояние от нее к центру. В зависимости от того, где вы поставите засечку будет зависеть размер итогового эллипса. Полученное расстояние откладываем вниз по вертикали, и ставим еще одну засечку. Такие же действия проделываем для горизонтали. Но здесь мы откладываем по два таких расстояния в каждую сторону. Крайние отрезки на горизонтали разбиваем приблизительно пополам и также ставим засечки.
Шаг 2. Соединяем крайние засечки на вертикали и горизонтали прямыми линями, получая форму ромба.
Шаг 3. Воспользовавшись двумя другими засечками на горизонтальной линии, нарисуем две вертикали до пересечения со сторонами ромба. Таким образом, мы получим четыре вспомогательные точки, по одной на каждой стороне ромба.
Шаг 4. Через центр и вспомогательные точки, полученные в прошлом шаге, проведем две наклонные прямые линии, которые будут параллельны сторонам ромба.
Шаг 5. Воспользовавшись двумя оставшимися засечками, проведем еще две вертикали до пересечения с наклонными линиями, полученными в прошлом этапе.
Шаг 6. Дугой изобразим часть овала.
Шаг 7. Второй дугой достроим первую четверть фигуры.
Шаг 8. По аналогии с 6-ым и 7-ым шагами строим верхнюю правую и нижнюю левую четверти овала.
Шаг 9. В завершающем шаге строится последняя нижняя четверть. После того как Вы сотрете все лишние линии у Вас должен получится правильный симметричный овал.
На данном этапе урок как нарисовать Овал правильно завершен. Теперь вы научились тому как правильно нарисовать овал. Желаем Вам творческих успехов!

ТОП 10: |
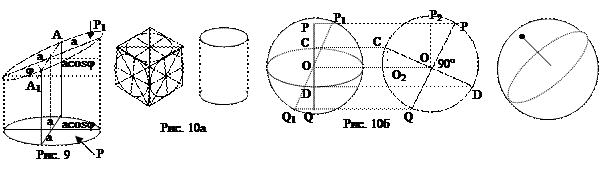
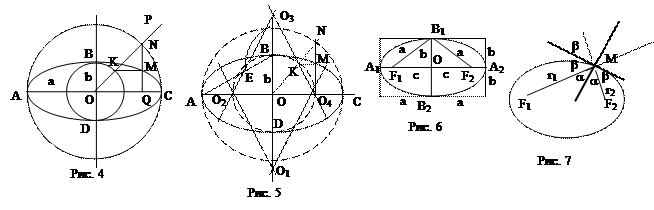
⇐ ПредыдущаяСтр 19 из 25Следующая ⇒ Процедуру построения эллипса из окружности путем сжатия можно выполнить с помощью циркуля и линейки следующим образом. Проводим две концентрические окружности радиуса OA=a и OВ=b. Через центр О проводим произвольный луч ОР. Через точки К и N, в которых OР встречает две окружности, проводим прямые, параллельные осям Х и Y. Эти прямые пересекутся в точке M. Ее ордината MQ меньше ординаты NQ точки N, лежащей на окружности радиуса а, причем MQ:NQ=b:a. Значит, точка M лежит на искомом эллипсе. Меняя направление луча ОР, получим новые точки эллипса (рис. 4). На рисунке 5 показано, как построить овал, похожий на эллипс с полуосями а и b (когда а и b отличаются друг от друга не слишком сильно), из дуг окружностей двух радиусов. Для этого надо на отрезке АВ от точки В отложить отрезок длины a-b, поставить точку Е и провести перпендикуляр через середину отрезка АЕ до пересечения с прямой BD. Точку пересечения с прямой BD назовем О1, точку пересечения с прямой АС назовем О2. Из этих точек, как из центров, проведем две сопрягающиеся дуги, радиусами О1В и О2А, соответственно. Центры О3 и О4 симметричны центрам О1 и О2. Если на том же чертеже построить опорные точки для эллипса методом сжатия окружности, будет видно, насколько сильно различаются линии овала и эллипса. Из уравнения эллипса можно заключить, что оси координат являются осями симметрии эллипса. Центр симметрии О называется
Сумма расстояний от вершины В1 эллипса до фокусов равна 2а. Для любой другой точки эллипса сумма расстояний r1+r2 от нее до фокусов тоже равна 2а (рис. 6). Обычно эллипс так и определяют – как геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина Нормаль и касательная к эллипсу являются биссектрисами соответственно внутреннего и внешнего углов между радиусами-векторами, проведенными из точки касания в фокусы (рис 7). На чертеже видно, что луч, выходящий из F1, отразившись от касательный по формуле «угол падения равен углу отражения», попадает в фокус F2.
Если а>b, то эллипс вытянут вдоль оси X, и число а называют большой полуосью. И фокусы расположены на оси X. Если же b>а, то эллипс вытянут вдоль оси Y. И фокусы расположены на оси Y. Для него все рассуждения сохраняются, но с заменой в них x на y и а на b, соответственно. Очевидно, что если а=b, то фокусное расстояние обращается в ноль, фокусы совпадают и эллипс превращается в окружность с радиусом а и с центром в начале координат. Так что окружность – это частный случай эллипса (рис. 8).
Уравнение Примеры 1.Составьте уравнение линии, полученной сжатием окружности х2+у2=25 по оси Y к оси Х с коэффициентом сжатия k, если k=3\5. Решение. Заданная окружность вписывается в квадрат со стороной 5. Следовательно, большая полуось эллипса а=5. По условию задачи 2.При проектировании окружности на какую-нибудь плоскость Р диаметр АА1, параллельный этой плоскости, проектируется в натуральную величину. А все хорды, перпендикулярные к этому диаметру, сокращаются в отношении, равном cosj, где j — угол между плоскостью окружности Р1 и плоскостью Р. Поэтому проекция окружности есть эллипс с большой осью 2 а=АА1 и коэффициентом сжатия k=cosj (малая полуось равна acosj) (рис. 9). 3. Эллипс используется в черчении для изображения окружности, расположенной не в плоскости чертежа, и в живописи при изображении окружности, не находящейся в плоскости, параллельной плоскости изображения (рис.10а). Шар изображают окружностью. Для того чтобы показать его объемность, в нем изображается «экватор» в виде эллипса и полюс Р (рис. 10б). Изображение полюсов получается параллельным переносом изображений полюсов на виде шара слева. Можно этот дополнительный чертеж не строить, а достаточно заметить, что из равенства: DО2СО=DР2РО=DР1РО=DQ1QО следует равенство: OC=OD=PP1=QQ1 и точки Р и Q выбираются так, чтобы выполнялись эти равенства.
|
۞ → Читать Урок Элементы черчения для начинающих
Первый способ начертить эллипс
Давайте начертим эллипс, вписанный в прямоугольник А.
Сначала при помощи циркуля найдите, где круг (показанный на рисунке А) пересекает длинную среднюю линию. Эти пересечения обозначены точками 1 и 2.
Воткните в эти точки булавки, а третью булавку (3) — в конце средней линии.
Крепко обвяжите эти булавки прочной льняной ниткой, как показано на рисунке В.
Удалите булавку 3 и очертите карандашом эллипс, как показано на рисунке С. Нитка должна быть постоянно равномерно натянута.
Второй способ построения
Вот еще один способ как начертить эллипс, вписанный в прямоугольник А.
Начертите два круга с центром в точке О. Диаметр одного круга должен быть равен ширине прямоугольника, а диаметр другого — длине прямоугольника, как показано на рисунке D.
Теперь проведите линии наподобие спиц колеса, как показано на рисунке Е.
Через точки пересечения спиц с малым кругом проведите линии, параллельные длинным сторонам. Через точки пересечения спиц с большим кругом проведите линии, параллельные коротким сторонам.
Эллипс проходит через точки пересечения линий, параллельных коротким сторонам и параллельных длинным сторонам, как показано на рисунке F.
Третий способ построения эллипса
Приводим еще один способ начертить эллипс определенной величины.
Возьмите полоску бумаги и отметьте на ней половину длины данного в качестве основы прямоугольника. Обозначьте точку буквой L, как показано на рисунке G.
Далее положите полоску вдоль линии ширины и буквой W обозначьте точку, отмечающую половину этой ширины, как показано на рисунке Н.
Теперь поместите бумажную полоску так, чтобы точка L касалась линии ширины, а точка W касалась линии длины, как показано на рисунке I.
Кончик полоски (обозначенный буквой Е) показывает, где проходит контур эллипса.
Продолжайте двигать полоску по кругу, пока не отметите столько точек, сколько вам нужно.
Этот метод подходит для вычерчивания эллипсов любой величины. При черчении после обозначения точек можно вычертить контур эллипса по лекалу.
Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).
Содержание:

Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).

То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.

Принципы рисования эллипсов:
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).

Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.

Рисуем эллипсы
Шаг 1. Для начала проведем две перпендикулярных оси.

Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.

Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.

Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.

Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.

Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.

Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Рисуем кружку

Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.

Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.

Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.

Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.

Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то — на глаз).

Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!

Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).

Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).

Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.

Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.

Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!

Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
 Юлия Отрубянникова
Юлия ОтрубянниковаКак правильно нарисовать (начертить) овал (эллипс)?
Чертишь ромб, по углам ставишь циркуль — и вперёд.. . Потренируешься — там много всяких вариантов, за 5 мин начертишь столько, сколько нужно…
Возьми две иголочки. Воткни их в лист бумаги на некотором расстоянии друг от друга. Сделай из ниточки колечко. Надень на иголочки. Возьми карандаш, подцепи колечко, натяни аккуратненько, и рисуй по «кругу». Вот и получится у тебя математически точный эллипс. Понятно, что величину, вытянутость, ты можешь регулировать…
Вот как это делается в черчении (правда, получается не точный эллипс, а очень похожая на него гладкая фигура из четырёх дуг) . 1) Рисуется ромб, в который необходимо вписать эллипс. 2) Вершины тупых углов ромба соединяются линиями с серединами противолежащих сторон. 3) Далее циркулем рисуются четыре дуги окружности как показано на рисунке <img src=»//otvet.imgsmail.ru/download/da304bc5c54d230574276285039457f7_i-136.jpg» >
Берешь круг и отрезаешь его!!!
очень смешно, Кристина. Нужен же овал, а не круг
Как нарисовать овал в прямоугольнике с помощью линейки и карандаша.
Для просмотра онлайн кликните на видео ⤵
Как начертить овал. Эллипс вписанный в ромб Подробнее
КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВ Подробнее

Как нарисовать круг в перспективе, рисуем эллипс, основы рисунка Подробнее

Как разметить эллипс, Как нарисовать эллипс Подробнее

Овал по заданным осям . Геометрические построения. Подробнее

Как начертить овал. Уроки черчения. Подробнее

OVALE DATO L’ASSE MAGGIORE Подробнее
How to make an Oval Подробнее

Основы ПЕРСПЕКТИВЫ в Рисунке Карандашом / Учимся Рисовать КАРАНДАШОМ Подробнее
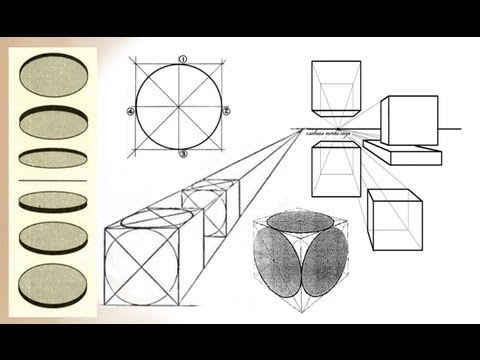
Как делать штриховку карандашом — теоретические основы. Подробнее

Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуля Подробнее

Как нарисовать эллипс — kalachevaschool.ru — Лайфхак 3 по рисованию от Дарьи Остапенко Подробнее
Как начертить эллипс. Уроки черчения. Подробнее

Как нарисовать идеальный круг от руки — 3 простых способа. Сможет каждый! Подробнее

Геометрия — Построение восьмиугольника Подробнее
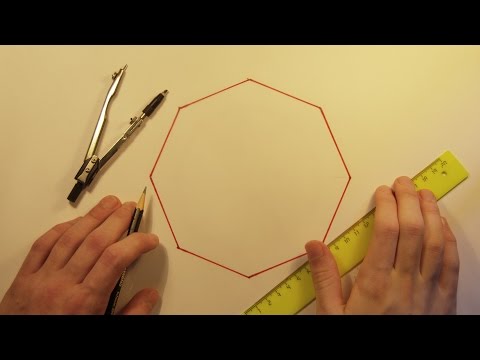
Как нарисовать эллипс — kalachevaschool.ru — Лайфхак по рисованию от Дарьи Остапенко Подробнее

КАК НАЧЕРТИТЬ, КАК РАЗМЕТИТЬ ОВАЛ, ЭЛЛИПС ПРОСТОЙ СПОСОБ Подробнее

5 ПРОСТЫХ ЛАЙФХАКОВ ДЛЯ ШКОЛЫ | Как нарисовать круг без циркуля Подробнее

3D треугольник / Как нарисовать 3D фигуру самому Подробнее
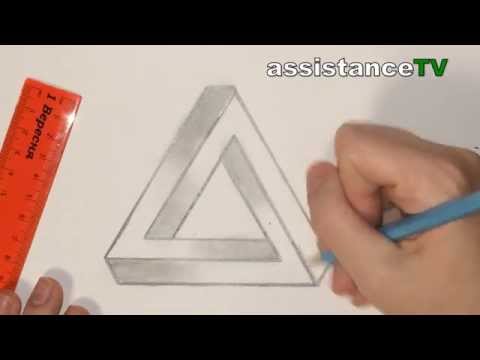

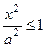 . Аналогично,
. Аналогично, 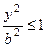 . Следовательно, длины сторон характеристического прямоугольника равны 2a и 2b, соответственно. Числа а и b — называются полуосямиэллипса. Большая полуось называется главной. Из точки В1 проведем дугу окружности радиуса а, точки пересечения этой дуги с осью симметрии эллипса А1А2 назовем F1 и F2. Это фокусыэллипса. Расстояние между ними обозначим через 2c. Ось симметрии, на которой расположены фокусы, называется фокальной осью, а величина с (расстояние от центра эллипса до фокуса) – фокусное расстояние эллипса.Фокусное расстояние эллипса – очень важная характеристика. Эллипс можно задавать и с помощью величины его главной полуоси и фокусного расстояния. Величины a b и c, являясь катетами и гипотенузой прямоугольного треугольника, связаны друг с другом простыми соотношениями (рис. 6):
. Следовательно, длины сторон характеристического прямоугольника равны 2a и 2b, соответственно. Числа а и b — называются полуосямиэллипса. Большая полуось называется главной. Из точки В1 проведем дугу окружности радиуса а, точки пересечения этой дуги с осью симметрии эллипса А1А2 назовем F1 и F2. Это фокусыэллипса. Расстояние между ними обозначим через 2c. Ось симметрии, на которой расположены фокусы, называется фокальной осью, а величина с (расстояние от центра эллипса до фокуса) – фокусное расстояние эллипса.Фокусное расстояние эллипса – очень важная характеристика. Эллипс можно задавать и с помощью величины его главной полуоси и фокусного расстояния. Величины a b и c, являясь катетами и гипотенузой прямоугольного треугольника, связаны друг с другом простыми соотношениями (рис. 6):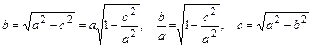
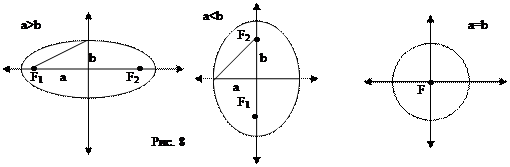
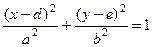
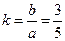 , отсюда b=3 и уравнение эллипса:
, отсюда b=3 и уравнение эллипса: