Как работать с процентами: Легко и просто решаем задачи на проценты – «Как правильно решать задачи на проценты?» – Яндекс.Знатоки

«Как правильно решать задачи на проценты?» – Яндекс.Знатоки

Что такое процент? Это часть от целого числа.
В чём ещё можно выразить часть от целого числа? В долях от единицы.
Целое число — это сколько процентов? Это 100%.
Можно целое число принять за 1 (единицу)? Можно.
Как найти часть от целого? Чтобы найти часть от числа, нужно целое число умножить на дробь, которая соответствует этой части.
Например. Задача.
Фруктовая корзина содержит яблоки, груши, персики и сливы массой 4 кг. Слив в этой корзине 20%-ов, персиков -10%-ов, груш — 30%-ов. Чему равна масса каждого фрукта в корзине?
Решение
20% — это в долях от единицы 0,2. Почему так? Потому что 1 меньше 100 во сколько раз? Правильно, в 100 раз. Значит, 20 разделить на 100, будет 0,2 (просто запятую переносим на два знака вперёд).
Вся фруктовая корзина — это целое и масса целого 4 кг. Чему будет равна масса 0,2 части этой корзины (это наши 20%)? Надо 4 кг умножить на 0,2. Получится 0,8 кг. Слив в корзине 800 грамм.
Таким же образом находим массу груш и персиков.
4 х 0,3 = 1,2 кг. Столько груш по массе в корзине или это и есть 30%.
4 х 0,1 = 0,4 кг. Столько персиков (10%).
А массу яблок расчитаем, как оставшуюся массу от остальных фруктов:
4 — 0,8 — 1,2 — 0,4 = 1,6 кг.
Когда я училась в школе (в советское время) нам учитель прочитала такой стишок: «Если часть найти желаешь, то на дробь ты умножаешь. Если часть тебе известна, хочешь целое найти, тут уж всем на удивленье делай поскорей деленье!» Эта присказка навечно засела в голове. Вот и вся премудрость!!! Всё! Про проценты.
Осталось про «удивленье». Задача. Раствор соли содержит 16 г соли, что сооветствует 10%-ам. Чему равна масса этого раствора соли?
Решение
Для удобства переведём проценты в доли от единицы. 10% — это 0,1.
Теперь делим: 16 : 0,1 = 160 г. Мы нашли массу этого 10%-го раствора соли. В 160 г 10%-ного раствора соли содержится 16 г соли
Можешь проверить. 160 х 0,1 = 16 г.

«Как правильно решать задачи на проценты?» – Яндекс.Кью

Что такое процент? Это часть от целого числа.
В чём ещё можно выразить часть от целого числа? В долях от единицы.
Целое число — это сколько процентов? Это 100%.
Можно целое число принять за 1 (единицу)? Можно.
Как найти часть от целого? Чтобы найти часть от числа, нужно целое число умножить на дробь, которая соответствует этой части.
Например. Задача.
Фруктовая корзина содержит яблоки, груши, персики и сливы массой 4 кг. Слив в этой корзине 20%-ов, персиков -10%-ов, груш — 30%-ов. Чему равна масса каждого фрукта в корзине?
Решение
20% — это в долях от единицы 0,2. Почему так? Потому что 1 меньше 100 во сколько раз? Правильно, в 100 раз. Значит, 20 разделить на 100, будет 0,2 (просто запятую переносим на два знака вперёд).
Вся фруктовая корзина — это целое и масса целого 4 кг. Чему будет равна масса 0,2 части этой корзины (это наши 20%)? Надо 4 кг умножить на 0,2. Получится 0,8 кг. Слив в корзине 800 грамм.
Таким же образом находим массу груш и персиков.
4 х 0,3 = 1,2 кг. Столько груш по массе в корзине или это и есть 30%.
4 х 0,1 = 0,4 кг. Столько персиков (10%).
А массу яблок расчитаем, как оставшуюся массу от остальных фруктов:
4 — 0,8 — 1,2 — 0,4 = 1,6 кг.
Когда я училась в школе (в советское время) нам учитель прочитала такой стишок: «Если часть найти желаешь, то на дробь ты умножаешь. Если часть тебе известна, хочешь целое найти, тут уж всем на удивленье делай поскорей деленье!» Эта присказка навечно засела в голове. Вот и вся премудрость!!! Всё! Про проценты.
Осталось про «удивленье». Задача. Раствор соли содержит 16 г соли, что сооветствует 10%-ам. Чему равна масса этого раствора соли?
Решение
Для удобства переведём проценты в доли от единицы. 10% — это 0,1.
Теперь делим: 16 : 0,1 = 160 г. Мы нашли массу этого 10%-го раствора соли. В 160 г 10%-ного раствора соли содержится 16 г соли
Можешь проверить. 160 х 0,1 = 16 г.

прибавить проценты к числу, подсчитать проценты, вычесть из числа

Проценты в современном мире крутятся повсюду. Не проходит ни дня без их использования. Покупая продукты – мы оплачиваем НДС. Взяв в банке кредит, мы выплачиваем сумму с процентами. Сверяя доходы, мы так же используем проценты.

Работа с процентами в Excel

Перед началом работы в Microsoft Excel вспомним школьные уроки математики, где вы изучали дроби и проценты.

Работая с процентами, помните, что один процент – это сотая часть (1%=0,01).

Выполняя действие прибавления процентов (к примеру, 40+10%), сначала находим 10% от 40, а только потом прибавляем основу (40).

Работая с дробями, не забывайте об элементарных правилах математики:

1. Умножения на 0.5 равно делению на 2.
2. Любой процент выражается через дробь (25%=1/4; 50%=1/2 и т.д.).

Считаем процент от числа

Чтобы найти процент от целого числа, разделите искомую долю на целое число и то что получилось умножьте на 100.

Пример №1. На складе хранится 45 единиц товара. 9 единиц товара продали за день. Сколько товара было продано в процентном соотношении?

9 — это часть, 45 — целое. Подставляем данные в формулу:

(9/45)*100=20%

В программе делаем следующее:

1. Для начала пропишем значение A1 и B1, в С1 выберем процентный тип расчетов и пропишем формулу =B1/A1.
2. После нажатия на «Enter» мы получим ответ, но появляется один нюанс. Ответ мы получаем в процентах. Он правильный, но мы не умножали на сто.

Как же это получилось? Задав процентный тип расчетов, программа самостоятельно допишет за вас формулу и поставит знак «%». Если бы мы задавали формулу самостоятельно (с умножением на сто), то знака «%» не было!

Пример №2. Решим обратную задачу. Известно, что на складе 45 единиц товара. Так же указано, что продано только 20%. Сколько всего единиц товара продали?

1. Найдем 20% из числа 45. Для этого задаем формулу (45*20)/100. Или воспользуемся похожей формулой (45/100)*20.
2. Чтобы не делить на 100, для нахождения результата попробуйте воспользоваться знаком «%».
3. Во всех случаях ответ получался одинаковым (9).

Пример №3. Попробуем обретенные знания на практике. Мы знаем цену за товар (см. рисунок ниже) и НДС (18%). Требуется найти сумму НДС.

Умножаем цену товара на процент, по формуле B1*18%.

Совет! Не забываем распространить эту формулу на остальные строчки. Для этого хватаем нижний правый угол ячейки и опускаем его до конца. Таким образом мы получаем ответ сразу на несколько элементарных задач.

Пример №4. Обратная задача. Мы знаем сумму НДС за товар и ставку (18%). Требуется найти цену товара.

1. Используем формулу (C1*100)/18.
2. Снова распространяем формулу до низа и получаем ответ.

Прибавляем и вычитаем

Начнем с прибавления. Будем рассматривать задачу на простом примере:

1. Нам дана цена товара. Необходимо прибавить к ней проценты НДС (НДС составляет 18%).
2. Если воспользоваться формулой B1+18%, то результат мы получим не верный. Так происходит потому, что нам необходимо прибавить не просто 18%, а 18% от первой суммы. В итоге мы получаем формулу В1+В1*0,18 либо В1+В1*18%.
3. Потяните вниз чтобы получить все ответы сразу.
4. На случай если вы воспользуетесь формулой В1+18 (без значка %), то ответы получатся со знаками «%», а результаты – не такими, как нам нужны.
5. Но эта формула тоже будет работать, если мы поменяем формат ячейки с «процентного» на «числовой».
6. Число знаков после запятой можете убрать (0) или выставить по своему усмотрению. 

Теперь попробуем вычесть процент из числа. Имея знания о прибавлении, вычитание не составит никакой сложности. Работать все будет при помощи подмены одного знака «+» на «-». Рабочая формула будет выглядеть так: В1-В1*18% или В1-В1*0,18.

Теперь найдем процент от всех продаж. Для этого просуммируем количество проданного товара и воспользуемся формулой B2/$B$7.

Вот такие элементарные задачи получились. Кажется все просто, но много людей допускают при этом ошибки.

Делаем диаграмму с процентами

Существует несколько типов диаграмм. Рассмотрим их по отдельности.

Круговая диаграмма

Попробуем создать круговую диаграмму. Она будет отображать проценты продажи товаров. Для начала ищем проценты от всех продаж.

Далее выделяем результаты и переходив во вкладку «Вставка» и выбираем диаграмму.

После, ваша диаграмма появится в таблице. Если вас не устроит ее место расположения, то переместите, потянув за рамки диаграммы.

Гистограмма

Для этого нам понадобятся данные. Например, данные о продажах. Для создания гистограммы нам потребуется выделить все числовые значения (кроме итога) и во вкладке «Вставить» выбрать гистограмму. Для создания гистограммы нам потребуется выделить все числовые значения (кроме итога) и во вкладке «Вставить» выбрать гистограмму.

График

Вместо гистограммы можно использовать график. К примеру, для слежки за прибылью гистограмма не подходит. Более уместным будет использование  графика. Вставляется график таким же способом как и гистограмма. Необходимо во вкладке «Вставить» выбрать график. На этот график можно наложить еще один. К примеру, график с убытками.

На этом мы заканчиваем. Теперь вы умеете рационально использовать проценты, строить диаграммы и графики в Microsoft Excel. Если у вас возник вопрос, на который статья не ответила, напишите нам. Постараемся вам помочь.

Вычисление процентов

В каждой естественной науке заключено столько истины, сколько в ней есть математики.

Вычисление процентов.

К числу типовых задач, предлагаемых на вступительных испытаниях, являются  задачи, связанные с вычислением процентов. Естественно, что для успешного решения таких задач необходимо знать свойства процентов и иметь хорошие навыки их применения при решении соответствующих задач. Особенно важно понимание процентов для абитуриентов – будущих студентов экономических специальностей.

В настоящей статье сначала приводятся основные понятия и обозначения, используемые при решении таких задач, а затем рассматриваются примеры решения задач на вычисление процентов.

Основные понятия и обозначения.

Под одним процентом от некоторой величины понимается ее одна сотая часть,

т.е.   величины  равна  .

Введем следующее обозначение: если значение величины  увеличивается  (уменьшается)  на  , то этот факт будем обозначать посредством записи   (соответственно, посредством  ).

Из определения понятия «процент» следует, что

 и  .

Если    и  , то имеет место  .

Аналогично, если    и  , то  .

 

Рассмотрим примеры текстовых задач на проценты, при решении которых применяются введенные выше обозначения.

Пример 1. Цена товара была увеличена на . На сколько процентов необходимо ее уменьшить, чтобы вернуться к первоначальной цене?  

Решение. Пусть  первоначальная цена товара. Тогда условие задачи можно (схематично) представить, как  .

Отсюда получаем уравнения    

,   ,    или  .

Ответ:  .

Пример 2

. Оклад молодого специалиста сначала повысили на , а затем (за прогулы) понизили на . На сколько процентов был увеличен первоначальный оклад?  

Решение. Пусть  первоначальный оклад. Тогда условие задачи можно записать в виде . Отсюда следует

,  ,    или  .

Ответ:  .

Пример 3. Численность населения города за два года увеличилась на  .  Найти средний ежегодный процент прироста населения.  

Решение. Пусть первоначальная численность населения. Тогда из условия следует  . Отсюда вытекает

, ,  или  .

Ответ:  .

Отметим, что при решении приведенных выше примеров в качестве первоначальной величины    можно принять единицу.

Пример 4. На сколько процентов следует увеличить радиус круга, чтобы площадь круга стала больше на ?.  

Решение. Так как площадь круга  , то из условия задачи следует  . Отсюда получаем

, ,    или  .

Ответ:  .

Пример 5. На сколько процентов следует уменьшить радиус шара, чтобы его объем стал меньше на ?   

Решение. Так как объем шара  , то из условия примера имеем  . Отсюда получаем

,  ,   

или  .

Ответ:  . 

Пример 6. На сколько процентов изменится произведение двух чисел, если одно из них увеличить, а другое уменьшить на ?

Решение. Схематично условие примера можно представить в следующем виде:  . Отсюда получаем

,  ,    

или   . Следовательно, произведение чисел уменьшится на .

Ответ:  .

Пример 7. Числитель дроби увеличили на . На сколько процентов следует уменьшить ее знаменатель, чтобы сама дробь увеличилась бы в два раза?

Решение. Условие примера схематично можно представить следующим образом:   . Отсюда получаем

,  ,      или   .

Ответ:  .

Пример 8. На сколько процентов следует уменьшить число рабочих завода, если при увеличении производительности труда на требуется увеличить объем готовой продукции только на ?

Решение. Пусть число рабочих, объем выпускаемой продукции, производительность труда рабочих (исходные значения).

Известно, что  . По условию задачи здесь имеем  

,   ,

,      или  .

Ответ:  .

Пример 9. Через какое наименьшее число лет денежный вклад, вложенный в банк под годовых, увеличится более чем в два раза?

Решение.

Первоначально составим схему решения данной задачи:   .

Отсюда вытекают неравенства

  или   .            Так как    и  ,  то  .

Ответ:   лет.

Пример 10. Однозначное число увеличили на 10 единиц. Если полученное  число  увеличить  на  такое  же  число ,  то  получится число 49. Найти число  .

Решение.  Из условия примера получаем     или

                               

Если первое уравнение системы разделить на второе, то получим

,    или   .

Корнями квадратного уравнения являются    и   или    и  . Так как по условию  однозначное число, то .

Ответ:  .

В заключение статьи рассмотрим задачи, при решении которых требуется вычислить процентное содержание определенных компонент в некоторых веществах, растворах или сплавах. При решении таких задач будем составлять схему решения, в которой символом «стрелка» выделяются те компоненты веществ (растворов, сплавов), которые используются при составлении уравнений.

Пример 11. Свежие фрукты содержат по массе воды,  а сухие – . Сколько сухих фруктов получится из свежих?

Решение. Условие задачи и схему ее решения представим посредством следующего чертежа (рис.1):

Так как при сушке свежих фруктов «фруктовая масса» является постоянной величиной, то    или  .

Ответ:

Пример 12. Сколько граммов воды необходимо добавить к раствора, содержащего сахара, чтобы содержание сахара в растворе уменьшилось до ?

Решение. На рис. 2 приведено схематическое изображение условия задачи и способа ее решения:

                                                                                 Рис. 2                                               

Так как содержание сахара в растворе до перемешивания с водой и после этого является постоянной величиной, то  

  или  .

Ответ:  .

Пример 13. Из железной руды выплавили металла, содержащего примесей. Сколько процентов примесей в руде?

Решение. Составим схему условия и способа решения заданной задачи (рис. 3) в следующем виде:

Поскольку содержание «чистого» металла (металла без примесей) в железной руде и в металле, полученного в процессе плавления, одинаково, то    или  .

Ответ:  .

Для более глубокого изучения методов решения текстовых задач на проценты мы рекомендуем обратиться к учебным пособиям, названия которых приведены в списке рекомендованной литературы.  

Рекомендуемая литература

1. Азаров А.И., Барвенов С.А., Федосенко В.С. Текстовые задачи. Пособие для учащихся. – Минск: ТетраСистемс, 2002.–208 с.

2. Сборник задач по математике для поступающих во втузы /Под ред. М.И. Сканави. – М.: Мир и Образование, 2013.–608 с.

3. Супрун В.П. Математика для старшеклассников: дополнительные разделы школьной программы. – М.: Ленанд /URSS, 2014. – 216 с.

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

 

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Как быстро посчитать процент от числа? Лайфхак от математика

Преподаватель математики из Британии поделился в твиттере простой формулой, с помощью которой можно мгновенно и без калькулятора рассчитать процент от числа. Лайфхак оценили даже учёные и уже вовсю применяют новые знания. Вопрос у пользователей соцсетей только один: почему чудо-трюкам их учит твиттер, а не учителя.

В России задачи, решаемые с помощью процентов, можно встретить в учебниках по математике для шестого класса. Тем не менее даже выпускникам школ и университетов бывает сложно быстро и в уме рассчитать процент от числа.

Пользователь твиттера по имени Бен Стефенс поделился арифметическим трюком для тех, кто не хочет растеряться над кредитным договором или при виде ценника со скидкой в магазине. Лайфхакер живёт в Британии и работает преподавателем математики.

Фокус Стефенса прост, но о нём вряд ли слышали представители гуманитарных профессий.

Для тех, кто не понял пост Бена: математик заметил, что, если числа в примере поменять местами, ответ не изменится. При этом в некоторых случаях считающему будет легче решить задачу. (Кстати, ответ на пример из поста: 3).

Легче всего лайфхак Стефенса объяснить на примере с участием 50 процентов и любого числа. Вам будет сложно найти 24 процента от числа 50, но намного легче найти 50 процентов от числа 24. Правильный ответ 12, и он будет верным решением для обеих задач.

За несколько дней математический твит Стефенса собрал свыше 5 тысяч репостов и 14 тысяч лайков. Оказалось, многие школьные преподаватели не рассказывали ученикам о таком фокусе.

Пользователи решили немедленно испытать силу лайфхака на собственных примерах. Пятёрки на экзамене им были бы обеспечены.

Хотя трюк Стефенса может существенно облегчить жизнь гуманитариев, он подходит не для всех задач. С этим нужно просто смириться.

Richard Young

ОригиналА сколько будет 43 процента от 87?

Pa ‏

ОригиналЭто будет 87 процентов от 43.

В сложных случаях любой желающий может воспользоваться классической формулой для нахождения процента от числа: (X*Y)/100. Чтобы найти 43 процента от числа 87, нужно умножить 43 на 87, а после разделить произведение на 100 (скорее всего, вам понадобится калькулятор). Благодаря расчётам мы узнали, что правильный ответ на задачу подписчиков Бена — 37,41.

Открытие Бена — настоящая неожиданность среди лайфхаков из социальных сетей. Зачастую люди делятся более жизненными фокусами. Например, объясняют, как без посторонних средств согреть лицо в лютую зиму, или рассказывают о самодельных приспособлениях, которые помогут вам не потерять свои AirPods.

Если вы любите новости об оригинальных лайфхаках и полезных изобретениях, подпишитесь на наш канал в телеграме. Это отличный способ стать настоящим гуру своей жизни.

Читайте на MedialeaksСын хвастался маме, что одноклассник — его двойник. И совместное фото мальчиков чуть не довело женщину до слёз

Проект по математике «Зачем нужны проценты?»

Проект по математике на тему:

«Зачем нужны проценты?»

Выполнил ученик 5А класса:

Еланцев Даниил

Проверила:

Грошева И.Г.

Новокузнецк, 2019г.

Для чего нужны проценты?

В повседневной жизни люди сталкиваются с процентами ежедневно.

При посещении магазинов мы видим яркие объявления о скидках и распродажах.

В последние годы в средствах массовой информации довольно часто можно услышать о повышении тарифов на коммунальные услуги. Как правило, все цифры озвучиваются в процентах.

Коммунальные платежи будут повышены в 2019 году в два этапа: на 1,7 % с 1 января и на 2,4 % с 1 июля

Кредиты в банковской сфере выдаются людям под процент. Также очень многие люди в целях безопасности и увеличения суммы денег хранят свои денежные средства в банках под процентами.

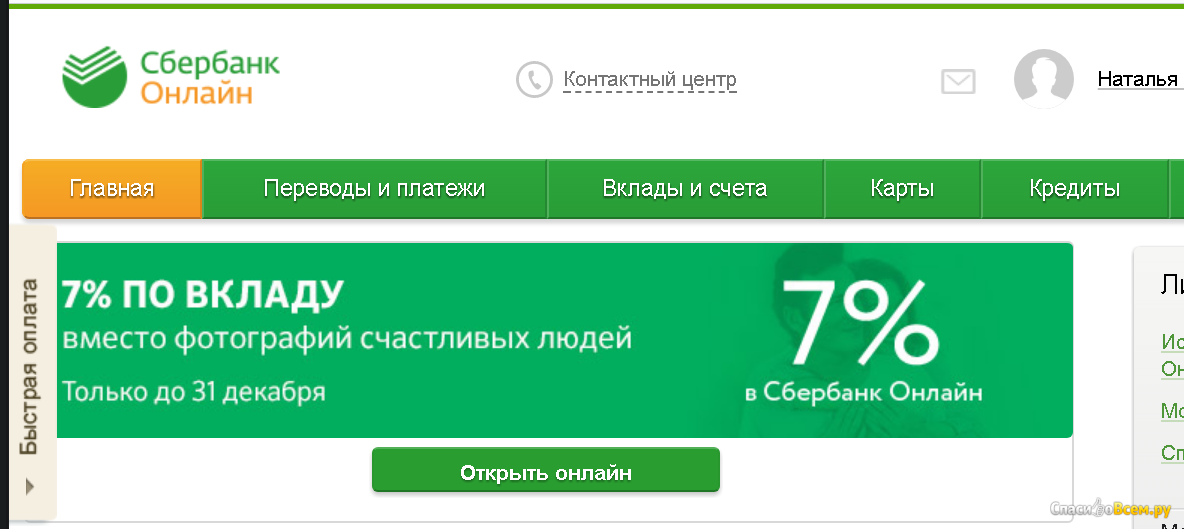
На выборах победа кандидата в президенты так же определяется в процентах.

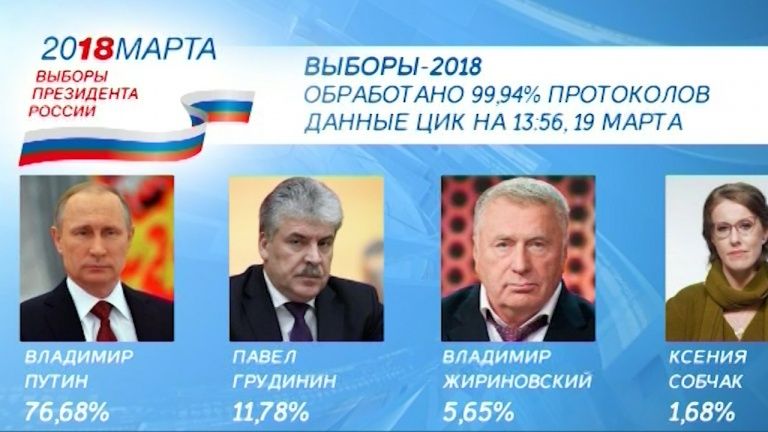
Медицинские работники ежедневно сталкиваются с умением рассчитать проценты, например, при инъекциях, для разбавления препарата. Покупая любое лекарство больной перед его использованием внимательно изучает инструкцию к нему, в которой подробно перечислен состав препарата с указанием процентного содержания всех входящих в него веществ.

Бухгалтер любого предприятия ежемесячно рассчитывает прибыль, полученную предприятием, начисляет заработную плату всем сотрудникам предприятия, производит отчисления в налоговую инспекцию, пенсионный фонд, в фонд социального страхования и прочие. Все отчисления рассчитываются индивидуально для каждого сотрудника, но при этом бухгалтер пользуется единой для всех процентной ставкой.

Умение вычислять проценты очень важно при приготовлении сплавов, например, для получения сплава золота 585 пробы необходимо 58.5% чистого золота и два основных металла: медь (33.5%) и серебро (8%). Из-за достаточно большого количества золота, внешний вид изделия из 585 пробы не тускнеет в процессе эксплуатации.

Так что же такое процент?

Процент — это одна сотая часть от числа. Процент записывается с помощью знака %.

Это понятие появилось в математике с развитием торговли, когда за взятые в долг деньги стали получать с должников какую-либо сумму сверх долга. Обычно эта сумма выражалась в сотых долях. Гораздо позже у нее появилось название — проценты. Слово «процент» произошла от двух латинских слов «pro centum»: «про»-на, и «центум»- сто, в переводе на русский язык процент означает «на сто». В ту пору проценты обозначали «cto». Но при наборе на печатной машинке эти три буквы приняли за дробь и напечатали знак «%». Так, опечатка дала жизнь новому математическому знаку.

— Чтобы перевести проценты в десятичную дробь, нужно разделить число на 100.

25% = 25:100 = 0,25

— Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100.

0,25 * 100 = 25%

— Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь, а потом умножить на 100.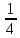

= 0, 25 * 100 = 25%

Проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств. В повседневной жизни нужно знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%, три четверти — 75%, одна пятая — 20%, а три пятых — 60%.

Знание наизусть соотношений из таблицы внизу облегчит решение многих задач. 1 = 100%

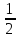
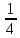
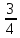
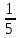
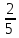
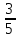
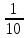
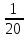
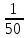
Десятичная дробь

0,5

0,25

0,75

0,2

0,4

0,6

0,1

0,05

0,02

Проценты

50%

25%

75%

20%

40%

60%

10%

5%

2%

Чаще всего проценты применяются для сравнения величин, для остроты восприятия и их значимости. Например, в городе Новокузнецке проживает 547 885 человек. А население России составляет 146 781 095 человек. То есть население Новокузнецка составляет 0,2% от всего населения страны. Сделав круговую или столбчатую диаграмму можно наглядно увидеть эту разницу.

Из диаграмм видно насколько мало население нашего города по сравнению со всей страной.

Интересные факты в процентах

Все живые животные и растительные существа состоят из воды: животные – на 75%, рыбы – на 75%, медузы – на 99%, картофель — на 76%, помидоры — на 90%, огурцы — на 95%, яблоки — на 85%, арбузы — на 96%. Даже человек состоит из воды. 86% воды содержится в теле у новорожденного и до 50% у пожилых людей.

Если человек теряет 2% воды от массы своего тела, то у него возникает сильная жажда. Если проценты потерянной воды увеличатся до 10, то у человека начнутся галлюцинации. При потере в 12% человек не сможет восстановиться без помощи врача. При потере в 20% человек умирает.

Вода не только дарит жизнь, но может и отнимать ее, 85% всех заболеваний в мире передается с помощью воды.

60% всех озёр мира находятся на территории Канады: более 3 000 000 озёр, занимающих 9% канадских земель.

Самая засушливая страна: Ливия. 99% Ливии покрыто пустыней.

Страна — крупнейший производитель кислорода в мире: Россия. В Сибири растёт примерно 25% мировых лесов, которые охватывают площадь больше, чем континентальная часть США, что делает Россию самым мощным в мире переработчиком углекислого газа в ценнейший кислород.

Итак, мы заметили, что проценты сопровождают нас повсюду. Следовательно, понимание процентов и умение производить, процентные расчеты в настоящее время необходимы каждому человеку, так как прикладное значение этой темы затрагивает все стороны нашей жизни: школьную, научную, хозяйственную, экономическую, финансовую, демографическую и другие.

Источники:

1. Васильева Л. В., Икон А. И. Проценты в нашей жизни и их применение // Юный ученый. — 2018. — №4. — С. 34-35. URL: http://yun.moluch.ru/archive/18/1279/ (дата обращения: 13.05.2019)

2. http://yun.moluch.ru/archive/18/1279/

3. https://intolimp.org/publication/proiekt-na-tiemu-protsienty/html

4. https://kopilkaurokov.ru/matematika/meropriyatia/nauchnyi_proiekt_protsienty_v_nashiei_zhizni

Процент — Википедия

Материал из Википедии — свободной энциклопедии

%

Проце́нт (нем. Prozent, от новолат. per centum «на сотню; сотая») — сотая часть; обозначается знаком «%»; используется для обозначения доли чего-либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть 85 кг. Справедливо также утверждение, что 200 % от 500 кг является 1000 кг, поскольку 1 % от 500 кг равен 5 кг, и 5 × 200 = 1000.

В Древнем Риме, задолго до существования десятичной системы счисления, вычисления часто производились с помощью дробей, которые были кратны 1/100. Например, Октавиан Август взимал налог в размере 1/100 на товары, реализовавшиеся на аукционе, это было известно как лат. centesima rerum venalium (сотая доля продаваемых вещей). Подобные расчёты были похожи на вычисление процентов.

При деноминации валюты в средние века вычисления со знаменателем 100 стали более привычными, а с конца XV века до начала XVI века данный метод расчёта стал повсеместно использоваться, судя по содержанию изученных материалов, содержащих арифметические вычисления. Во многих из этих материалов данный метод применялся для расчёта прибыли и убытка, процентных ставок, а также в «тройном правиле»^[1]. В XVII веке данная форма вычислений стала стандартом для представления процентных ставок в сотых долях^[2].

В России понятие процента впервые ввёл Пётр I. Но считается, что подобные вычисления начали применяться в Смутное время, как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек^{[источник не указан 1895 дней]}.

Соотношение процентов и десятичных дробей[править | править код]

• 0 % = 0;
• 0,07 % = 0,0007;
• 45,1 % = 0,451;
• 76,69 % = 0,7669;
• 100 % = 1;
• 146 % = 1,46;
• 200 % = 2
• 500 % = 5

• «Работать за проценты» — работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.
• «Процентщик» — человек, ссужающий деньги под большие проценты, ростовщик.

Изменения показателей, которые сами исчисляется в процентах, обычно выражают не в процентах от исходного показателя, а в так называемых «процентных пунктах», выражающих разность нового и старого значений показателя^[3]. Например, если в некой стране индекс деловой активности вырос с 50 % до 51 %, то он изменился на 51 %−50 %50 %=150=0,02=2 %{\displaystyle {\frac {51~\%-50~\%}{50~\%}}={\frac {1}{50}}=0{,}02=2~\%}, а в процентных пунктах изменение составило 51 %−50 %=1 %{\displaystyle 51~\%-50~\%=1~\%}.

Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остаётся только одна возможность вычисления процента, а именно деление разности на меньшее из двух чисел с последующим умножением результата на 100.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)