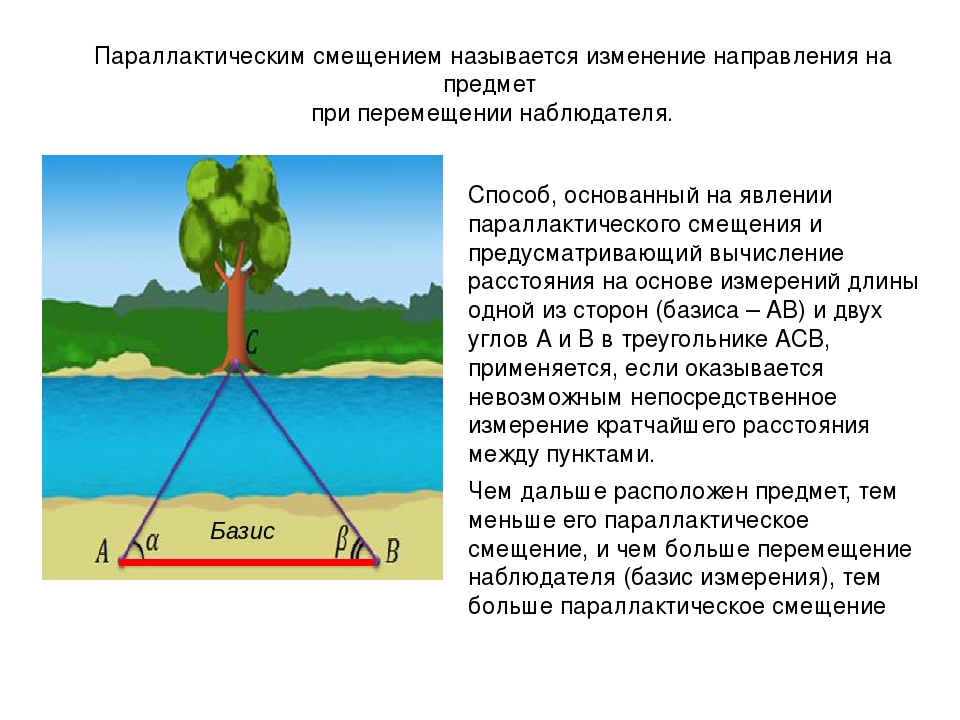
Мнимое смещение обьекта, 9 (девять) букв
Вопрос с кроссворда
Ответ на вопрос «Мнимое смещение обьекта «, 9 (девять) букв:
параллакс
Альтернативные вопросы в кроссвордах для слова параллакс
Фильм Алана Пакулы «Заговор «…»
Изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя
Смещение звезды при перемещении наблюдателя
Оптическое явление — видимое смещение двух изображений
Фильм Алана Пакулы «Заговор «…»
Видимое изменение положения объекта (напр., звезды), происходящее из-за изменения положения наблюдателя
Определение слова параллакс в словарях
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова. Значение слова в словаре Новый толково-словообразовательный словарь русского языка, Т.
Ф. Ефремова.
Википедия Значение слова в словаре Википедия
Параллакс — вымышленный космический злодей, появлявшийся в комиксах компании DC Comics . Создан писателем Роном Мартцем и художником Дэррилом Бэнксом, Параллакс впервые появился в номере Green Lantern (vol. 3) #50 в январе 1994 года, где стал новой протагонистической …
Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
(греч. parallaxis — уклонение) (астр.). угол измеряющий видимое смещение светила при перемещении наблюдателя из одной точки пространства в другую. Суточный параллакс (угол между направлениями на светило из данного места земной поверхности …Примеры употребления слова параллакс в литературе.
Труднее пользоваться записями акселерометра для определения направления движения Все эти координатные системы, аппараты, дифференциальные исчисления, небесные координаты, эклиптики, знаки зодиака, параллаксы, измерения широт, ортогональные проекции, перигелии, афелии, скорости В многочисленных чертежах чертовски трудно разобраться.
Ту бесчисленность миров, о которой рассказывал Сен-Савен, следовало искать не только по другую сторону созвездий, но и посреди пузыря в пространстве, для которого Роберт, весь сводящийся к оку, ныне выступал источником неисчисляющихся параллаксов.
Этот Зонд позволил им измерить параллакс нескольких сравнительно далеких звезд.
Потребовалось еще трое суток упорной и кропотливой работы, всего на свете от измерения точного перемещения источника до интерферометрического анализа его пространственной протяженности, прежде чем оба брата согласились признать: параллакс, наблюдаемый из юпитерианских точек Л-4 и Л-5, реален.
Мы измерили параллакс, провели целую серию оптических и спектральных исследований, а также ряд независимых проверок.
Как заметил Соларатов, именно прицел являлся слабейшим элементом всей конструкции он был расположен параллельно оси винтовки, но не над стволом, а сбоку, и это создавало трудности с определением параллакса, которые необходимо было преодолеть.
Источник: библиотека Максима Мошкова
Мнимое Смещение Обьекта 9 Букв
Решение этого кроссворда состоит из 9 букв длиной и начинается с буквы П Ниже вы найдете правильный ответ на Мнимое смещение обьекта 9 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
ПАРАЛЛАКС
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Параллакс
- Видимое изменение положения объекта (напр.
, звезды), происходящее из-за изменения положения наблюдателя - Параллакс
- Переведите на греческий язык «отклонение» 9 букв
- Угол 9 букв
- Видимое изменение положения объекта (напр 9 букв
- Оптическое явление- видимое смещение двух изображений 9 букв
, звезды), происходящее из-за изменения положения наблюдателяпохожие кроссворды
- Мнимое смещение обьекта
- Нечто несуществующее, мнимое, ложное
- Мнимое предсказание
- Нечто несуществующее, мнимое, ложное 6 букв
- Мнимое божество 4 буквы
- Нечто мнимое, ложное 6 букв
- Косоглазие мнимое
- Мнимое доказательство 6 букв
- фикция, вещь или дело мнимое, вымысел, плод воображения, мороки
- Уловка, мнимое доказательство, при недостаточно внимательном логич
- Мнимое лекарство, исцеляющие от всех болезней
- Смещение всей матки кпереди относительно оси таза
- Смещение костей в суставе
- Смещение концов костей
- Ненормальное смещение какого-либо органа
2.
1 Перемещение – Физика колледжаПерейти к содержимому
Глава 2 Одномерная кинематика
Сводка
- Определение положения, перемещения, расстояния и пройденного расстояния.
- Объясните взаимосвязь между положением и перемещением.
- Различать перемещение и пройденное расстояние.
- Рассчитать смещение и расстояние, учитывая начальное положение, конечное положение и путь между ними.
Чтобы описать движение объекта, вы должны сначала уметь описать его — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам в этой системе отсчета.
Например, запуск ракеты может быть описан с точки зрения положения ракеты относительно Земли в целом, а положение профессора может быть описано с точки зрения того, где он находится по отношению к ближайшей доске. (См. рис. 2.) В других случаях мы используем системы отсчета, которые не стационарны, а находятся в движении относительно Земли. Например, для описания положения человека в самолете в качестве системы отсчета мы используем самолет, а не Землю. (См. рис. 3.)
Если объект перемещается относительно системы отсчета (например, если профессор движется вправо относительно белой доски или пассажир движется к задней части самолета), то положение объекта изменяется. Это изменение положения известно как . Слово «смещение» подразумевает, что объект сдвинулся или был смещен.
ПЕРЕМЕЩЕНИЕ
Смещение — это изменение положения объекта:
[латекс]{\Delta{x}=x_f-x_0}[/latex]
, где [latex]{\Delta{x}}[/latex] — смещение, [latex]{x_f}[/latex] — конечная позиция, а [latex]{x_0}[/latex] — начальная позиция .
В этом тексте заглавная греческая буква [латекс]{\дельта}[/латекс] (дельта) всегда означает «изменение» любой величины, следующей за ней; таким образом, [latex]{\Delta{x}}[/latex] означает изменение позиции . Всегда вычисляйте смещение, вычитая начальное положение [латекс]{x_0}[/латекс] из конечного [латекс]{x_f}[/латекс].
Обратите внимание, что единицей СИ для перемещения является метр (м) (см. главу 1.2 Физические величины и единицы), но иногда используются километры, мили, футы и другие единицы длины. Имейте в виду, что когда в задаче используются единицы измерения, отличные от метра, вам может потребоваться преобразовать их в метры, чтобы завершить расчет.
Рисунок 2. Профессор ходит влево и вправо во время лекции. Ее положение относительно Земли определяется как x . Смещение профессора относительно Земли на +2,0 м показано стрелкой, указывающей вправо. Рисунок 3. Пассажир перемещается со своего места в заднюю часть самолета.
Его местоположение относительно самолета определяется как x . Смещение пассажира на -4,0 м относительно самолета показано стрелкой в направлении задней части самолета. Обратите внимание, что стрелка, обозначающая его смещение, в два раза длиннее стрелки, обозначающей смещение профессора (он перемещается в два раза дальше) на рис. 2.Обратите внимание, что смещение имеет не только величину, но и направление. Перемещение профессора — 2,0 м вправо, перемещение авиапассажира — 4,0 м назад. В одномерном движении направление может быть указано со знаком плюс или минус. Когда вы начинаете решать задачу, вы должны выбрать положительное направление (обычно это будет вправо или вверх, но вы можете выбрать любое положительное направление). Начальное положение профессора — [латекс]{x_0=1,5\текст{м}}[/латекс], а его конечное положение — [латекс]{х_f=3,5\текст{м}}[/латекс]. Таким образом, ее водоизмещение равно
[латекс]{\Delta{x}=x_f-x_0=3,5\текст{м}-1,5\текст{м} =+2,0\текст{м}}[/латекс].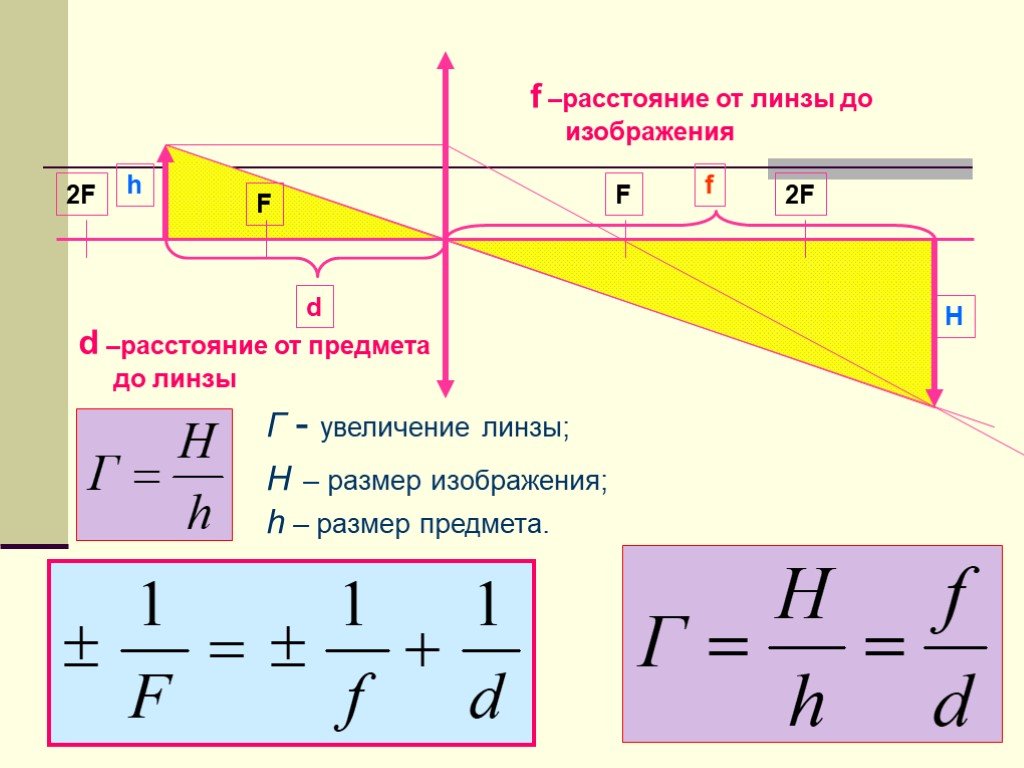
В этой системе координат движение вправо считается положительным, а движение влево отрицательным. Точно так же начальное положение пассажира самолета [latex]{x_0=6.0\text{ m}}[/latex], а его конечное положение — [latex]{x_f=2.0\text{ m}}[/latex], поэтому его смещение
[латекс] {\ Delta {x} = x_f-x_0 = 2,0 \ текст {м} -6,0 \ текст {м} = -4,0 \ текст {м}} [/латекс].
Его смещение отрицательное, потому что он движется к задней части плоскости или в отрицательном направлении x в нашей системе координат.
Хотя смещение описывается в терминах направления, расстояние — нет. определяется как величина или размер смещения между двумя позициями . Обратите внимание, что расстояние между двумя положениями не равно расстоянию, пройденному между ними. равно общей длине пути между двумя позициями . Расстояние не имеет направления и, следовательно, не имеет знака. Например, расстояние, которое проходит профессор, равно 2,0 м.
Расстояние, которое проходит пассажир самолета, равно 4,0 м.
ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ: ПРОБЕГЕННОЕ РАССТОЯНИЕ VS. ВЕЛИЧИНА ПЕРЕМЕЩЕНИЯ
Важно отметить, что пройденное расстояние , однако, может быть больше, чем величина смещения (под величиной мы подразумеваем именно величину смещения без учета его направления, т. е. просто число с единицей). Например, профессор может ходить взад и вперед много раз, возможно, пройдя расстояние 150 м во время лекции, но все же оказаться всего в 2,0 м справа от своей начальной точки. В этом случае ее перемещение составило бы +2,0 м, величина ее смещения составила бы 2,0 м, а пройденное ею расстояние составило бы 150 м. Мы почти всегда имеем дело со смещением и величиной смещения и почти никогда с пройденным расстоянием. Один из способов подумать об этом — предположить, что вы отметили начало и конец движения. Смещение — это просто разница в положении двух меток, и оно не зависит от пути, пройденного при перемещении между двумя метками.
Однако пройденное расстояние — это общая длина пути, пройденного между двумя отметками.
- Кинематика — это изучение движения без учета его причин. В этой главе оно ограничивается движением по прямой линии, называемым одномерным движением.
- Смещение — это изменение положения объекта.
- В символах смещение [латекс]{\Delta{x}}[/латекс] определяется как
[латекс]{\Delta{x} =x_f -x_0}[/латекс]
, где [латекс]{х_0}[/латекс] — это начальная позиция, а [латекс]{x_f}[/латекс] — это конечное положение. В этом тексте греческая буква [латекс]{\дельта}[/латекс] (дельта) всегда означает «изменение» того количества, которое следует за ней. Единицей водоизмещения в СИ является метр (м). Смещение имеет направление, а также величину.
- Когда вы начинаете решать задачу, укажите, какое направление будет положительным.
- Расстояние — это величина смещения между двумя положениями.
- Пройденное расстояние — это общая длина пути, пройденного между двумя позициями.
Глоссарий
- Кинематика
- изучение движения без рассмотрения его причин
- позиция
- местоположение объекта в определенное время
- рабочий объем
- изменение положения объекта
- расстояние
- величина смещения между двумя положениями
- пройденное расстояние
- общая длина пути, пройденного между двумя позициями
License
College Physics by OpenStax распространяется под лицензией Creative Commons Attribution 4.0 International License, если не указано иное.
Поделиться этой книгой
Поделиться в Твиттере
Три закона Кеплера
В начале 1600-х годов Иоганн Кеплер предложил три закона движения планет. Кеплер смог обобщить тщательно собранные данные своего наставника Тихо Браге тремя утверждениями, описывающими движение планет в солнечной системе с центром в центре Солнца.
Попытки Кеплера объяснить основные причины таких движений больше не принимаются; тем не менее, сами фактические законы по-прежнему считаются точным описанием движения любой планеты и любого спутника.
Три закона движения планет Кеплера можно описать следующим образом:
- Путь планет вокруг Солнца имеет эллиптическую форму, при этом центр Солнца находится в одном фокусе. (Закон эллипсов)
- Воображаемая линия, проведенная от центра Солнца к центру планеты, заметает равные площади за равные промежутки времени. (Закон равных площадей)
- Отношение квадратов периодов любых двух планет равно отношению кубов их средних расстояний от Солнца. (Закон Гармоний)
Первый закон Кеплера, иногда называемый законом эллипсов, объясняет, что планеты вращаются вокруг Солнца по траектории, описываемой как эллипс. Эллипс можно легко построить с помощью карандаша, двух кнопок, веревки, листа бумаги и куска картона.
Прикрепите лист бумаги к картону двумя кнопками. Затем завяжите нить в петлю и оберните петлю вокруг двух кнопок. Возьмите карандаш и тяните за нитку, пока карандаш и две кнопки не образуют треугольник (см. схему справа). Затем начните обводить путь карандашом, плотно обмотав нитку вокруг кнопок. В результате получится эллипс. Эллипс — это особая кривая, в которой сумма расстояний от каждой точки кривой до двух других точек является постоянной величиной. Две другие точки (обозначенные здесь положениями галса) известны как 9-я точка.0020 фокусов эллипса. Чем ближе друг к другу эти точки, тем больше эллипс напоминает форму круга. На самом деле круг — это частный случай эллипса, в котором два фокуса находятся в одном месте. Первый закон Кеплера довольно прост: все планеты вращаются вокруг Солнца по траектории, напоминающей эллипс, причем Солнце находится в одном из фокусов этого эллипса.
Второй закон Кеплера, иногда называемый законом равных площадей, описывает скорость, с которой любая планета будет двигаться по орбите вокруг Солнца.
Скорость, с которой любая планета движется в космосе, постоянно меняется. Планета движется быстрее всего, когда она находится ближе всего к Солнцу, и медленнее всего, когда она дальше всего от него. Однако если воображаемую линию провести от центра планеты к центру Солнца, то эта линия охватит ту же площадь за равные промежутки времени. Например, если воображаемую линию провести от земли к солнцу, то площадь, заметаемая этой линией за каждый 31-дневный месяц, будет одинаковой. Это изображено на диаграмме ниже. Как видно на диаграмме, области, образованные, когда Земля находится ближе всего к Солнцу, можно аппроксимировать широким, но коротким треугольником; тогда как области, образованные, когда Земля находится дальше всего от Солнца, могут быть аппроксимированы узким, но длинным треугольником. Эти области имеют одинаковый размер. С основание этих треугольников являются самыми короткими, когда Земля находится дальше всего от Солнца, Земля должна двигаться медленнее, чтобы эта воображаемая площадь была того же размера, что и когда Земля находится ближе всего к Солнцу.
Закон гармоний
Третий закон Кеплера, иногда называемый законом гармоний , сравнивает период обращения и радиус орбиты планеты с таковыми у других планет. В отличие от первого и второго законов Кеплера, описывающих характеристики движения одной планеты, третий закон сравнивает характеристики движения разных планет. Проводится сравнение, заключающееся в том, что отношение квадратов периодов к кубам их средних расстояний от Солнца одинаково для каждой из планет. В качестве иллюстрации рассмотрим период обращения и среднее расстояние от Солнца (радиус орбиты) для Земли и Марса, как указано в таблице ниже.
Планета | Период | Среднее | T 2 /R 3 |
Земля | 3,156 x 10 7 с | 1,4957 x 10 11 | 2,977 x 10 -19 |
Марс | 5,93 x 10 7 с | 2,278 x 10 11 | 2,975 x 10 -19 |
Обратите внимание, что соотношение T 2 /R 3 для Земли такое же, как и для Марса.
На самом деле, если вычислить одно и то же отношение T 2 /R 3 для других планет, можно обнаружить, что это отношение является почти одинаковым для всех планет (см. таблицу ниже). Удивительно, но на каждой планете одинаковый T 2 /R 3 соотношение.
Планета | Период | Среднее | T 2 /R 3 |
Меркурий | 0,241 | 0,39 | 0,98 |
Венера | . | 0,72 | 1.01 |
Земля | 1,00 | 1,00 | 1,00 |
Марс | 1,88 | 1,52 | 1.01 |
Юпитер | 11,8 | 5,20 | 0,99 |
Сатурн | 29,5 | 9,54 | 1,00 |
Уран | 84,0 | 19.18 | 1,00 |
Нептун | 165 | 30. | 1,00 |
Плутон | 248 | 39,44 | 1,00 |
615
06( ПРИМЕЧАНИЕ : Среднее значение расстояния дано в астрономических единицах, где 1 а. 1 земной год — это время, необходимое Земле для обращения вокруг Солнца — 3,156 х 10 7 секунд. )
Третий закон Кеплера дает точное описание периода и расстояния по орбите планеты вокруг Солнца. Кроме того, тот же закон, который описывает отношение T 2 /R 3 для орбит планет вокруг Солнца, также точно описывает отношение T 2 /R 3 для любого спутника (будь то луна или человек). спутник) о любой планете. В этом Т 9 есть что-то гораздо более глубокое.0217 2 /R 3 отношение — то, что должно относиться к основным фундаментальным принципам движения.
В следующей части Урока 4 эти принципы будут исследованы по мере того, как мы будем проводить связь между принципами кругового движения, обсуждавшимися в Уроке 1, и движением спутника.
Как Ньютон расширил свое понятие гравитации, чтобы объяснить движение планет?
Сравнение Ньютоном ускорения Луны с ускорением объектов на Земле позволило ему установить, что Луна удерживается на круговой орбите силой тяжести — силой, которая находится в обратной зависимости от расстояния между центрами двух объектов. . Установление гравитации как причины орбиты Луны не обязательно означает, что гравитация является причиной орбит планеты. Как же тогда Ньютон представил достоверные доказательства того, что сила гравитации соответствует требованию центростремительной силы для эллиптического движения планет?
Напомним, что ранее в Уроке 3 Иоганн Кеплер предложил три закона движения планет. Его закон гармонии предполагал, что отношение квадрата периода обращения ( T 2 ) к среднему радиусу обращения в кубе ( R 3 ) равно одному и тому же значению k для всех планет, обращающихся по орбите.
солнце. Известные данные для вращающихся планет предполагают следующее среднее соотношение:
к = 2,97 х 10 -19 с 2 /м 3 = (T 2 )/(R 3 )
Ньютон смог объединить закон всемирного тяготения с принципами кругового движения, чтобы показать, что если сила тяжести обеспечивает центростремительную силу для почти круговых орбит планет, то значение 2,97 x 10 -19 с 2 /m 3 можно было предсказать для отношения T 2 /R 3 . Вот рассуждения, используемые Ньютоном:
Рассмотрим планету с массой M планету , совершающую почти круговое движение вокруг Солнца с массой M Солнце . Суммарная центростремительная сила, действующая на эту вращающуюся вокруг планеты, определяется соотношением
F нетто = (M планета * v 2 ) / R
Эта результирующая центростремительная сила является результатом гравитационной силы, которая притягивает планету к Солнцу, и может быть представлена как
F грав = (G* M планета * M Солнце ) / R 2
Поскольку F grav = F net , приведенные выше выражения для центростремительной силы и силы тяжести равны.
Таким образом,
(M планета * v 2 ) / R = (G* M планета * M Солнце ) / R 2
Так как скорость объекта на почти круговой орбите может быть аппроксимирована как v = (2*pi*R) / T,
v 2 = (4 * pi 2 * R 2 ) / T 2
Подстановка выражения для v 2 в приведенное выше уравнение дает
(M планета * 4 * pi 2 * R 2 ) / (R • T 2 ) = (G* M планета * M Солнце ) / R 2
Путем перекрестного умножения и упрощения уравнение можно преобразовать в
T 2 / R 3 = (M планета * 4 * пи 2 ) / (G* M планета * M Солнце 1 )
Затем массу планеты можно вычесть из числителя и знаменателя правой части уравнения, что даст
T 2 / R 3 = (4 * pi 2 ) / (G * M Sun )
Правая часть приведенного выше уравнения будет иметь одинаковое значение для каждой планеты, независимо от массы планеты.
Следовательно, разумно, что отношение T 2 /R 3 будет одинаковым значением для всех планет, если сила, удерживающая планеты на их орбитах, является силой гравитации. Универсальный закон всемирного тяготения Ньютона предсказывает результаты, которые согласуются с известными планетарными данными и обеспечивают теоретическое объяснение закона гармонии Кеплера.
Расследуй!
Ученые знают о планетах гораздо больше, чем во времена Кеплера. Используйте виджет The Planets , чтобы узнать, что известно о различных планетах.
Проверьте свое понимание
1. Наше понимание эллиптического движения планет вокруг Солнца продолжалось несколько лет и включало вклад многих ученых.
а. Какому ученому приписывают сбор данных, необходимых для поддержки эллиптического движения планеты?
б.
с. Какому ученому приписывают точное объяснение данных?
Какому ученому приписывают долгую и сложную задачу анализа данных?
2. Галилею часто приписывают раннее открытие четырех из множества спутников Юпитера. Луны, вращающиеся вокруг Юпитера, следуют тем же законам движения, что и планеты, вращающиеся вокруг Солнца. Один из спутников называется Ио — его расстояние от центра Юпитера составляет 4,2 единиц и обращается вокруг Юпитера за 1,8 земных дня. Другая луна называется Ганимед; это 10,7 единицы от центра Юпитера. Сделайте предсказание периода Ганимеда, используя закон гармоний Кеплера.
3. Предположим, открыта небольшая планета, которая находится в 14 раз дальше от Солнца, чем Земля от Солнца (1,5 x 10 11 м). Используйте закон гармоний Кеплера, чтобы предсказать период обращения такой планеты. ДАННО: Т 2 /R 3 = 2,97 x 10 -19 с 2 /м 3
4.
Среднее орбитальное расстояние Марса в 1,52 раза больше среднего орбитального расстояния Земли. Зная, что Земля совершает оборот вокруг Солнца примерно за 365 дней, используйте закон гармоний Кеплера, чтобы предсказать время обращения Марса вокруг Солнца.
Данные о радиусе и периоде обращения четырех крупнейших спутников Юпитера приведены в таблице ниже. Масса планеты Юпитер 1,9.х 10 27 кг. Основывайте свои ответы на следующие пять вопросов на этой информации.
Луна Юпитера | Период(ы) | Радиус (м) | Т 2 /Р 3 |
Ио | 1,53 x 10 5 | 4,2 x 10 8 | а. |
Европа | 3,07 x 10 5 | 6,7 x 10 8 | б. |
Ганимед | 6,18 x 10 5 | 1,1 x 10 9 | с. |
Каллисто | 1,44 x 10 6 | 1,9 х 10 9 | д. |
5. Определите отношение T 2 /R 3 (последний столбец) для спутников Юпитера.
6. Какую закономерность вы наблюдаете в последнем столбце данных? Какой закон Кеплера это подтверждает?
7.
Используйте графические возможности калькулятора TI для построения графика T 2 в сравнении с R 3 (T 2 следует отложить по вертикальной оси) и определить уравнение прямой. Запишите уравнение в форме пересечения наклона ниже.
См. график ниже.
8. Как отношение T 2 /R 3 для Юпитера (как показано в последнем столбце таблицы данных) соотносится с отношением T 2 /R 3 , найденным в № 7 (т.е. , наклон линии)?
9. Как отношение T 2 /R 3 для Юпитера (как показано в последнем столбце таблицы данных) соотносится с отношением T 2 /R 3 , найденным с использованием следующего уравнение? (G = 6,67×10 -11 N *M 2 / KG 2 и M Jupiter = 1,9 x 10 27 кг)
