По вертикали и горизонтали как это: История искусств

Содержание

#1 Прямые линии — вертикали и горизонтали :: DIY Photo School

Итак, поехали!
Речь в первом выпуске пойдёт о вертикальных и горизонтальных линиях.

Я постарался сохранить основной смысл, немного сократив исходные тексты и по-возможности упростив описание. Если всё же встретите незнакомые слова, спросите в комментариях, особенно если это мешает понять идею. Ничего зазорного в этом нет, мы все тут новички.

Настоятельно рекомендую пойти и почитать сами источники, особенно Майкла Фримана (ссылки в конце поста). Это займёт 10-30 минут. Некоторые мысли и идеи, а главное авторские иллюстрации, не попали в выпуск.

P.S: Картинки в посте видно?

Линии

Все изображения состоят из совокупности линий, форм и очертаний. В фотографии линии проявляются менее явно, чем в изобразительном искусстве, и обычно они воображаемые. Роль линии часто играют края видимых предметов или последовательность объектов.

При визуальном определении линий наибольшую роль играет контраст — между светом и тенью, участками разного цвета, текстурами и формами. Поскольку рамка фотографии сама состоит из линий, это побуждает глаз сравнивать угол и длину линий рамки и линий изображения.

Линии характеризуются динамическими свойствами — направлением и движением. С помощью линий, автор может направлять взгляд зрителя по пространству кадра к объекту.

Линии обладают и выразительными свойствами. Мощные чёткие линии могут выражать смелость, тонкие изгибающиеся линии намекают на деликатность и т.д.

Разные формы линий вызывают определённые ассоциации. Горизонтальные и вертикальные линии порождают ощущение силы и мощи и некой статичности. Диагональные линии создают впечатление движения неподвижного изображения.

Горизонтальные, вертикальные и наклонные линии (диагонали), вносят свой вклад в создание настроения, вызываемого изображением. Угол наклона и соотношение с размером рамки определяют влияние линии на восприятие изображения.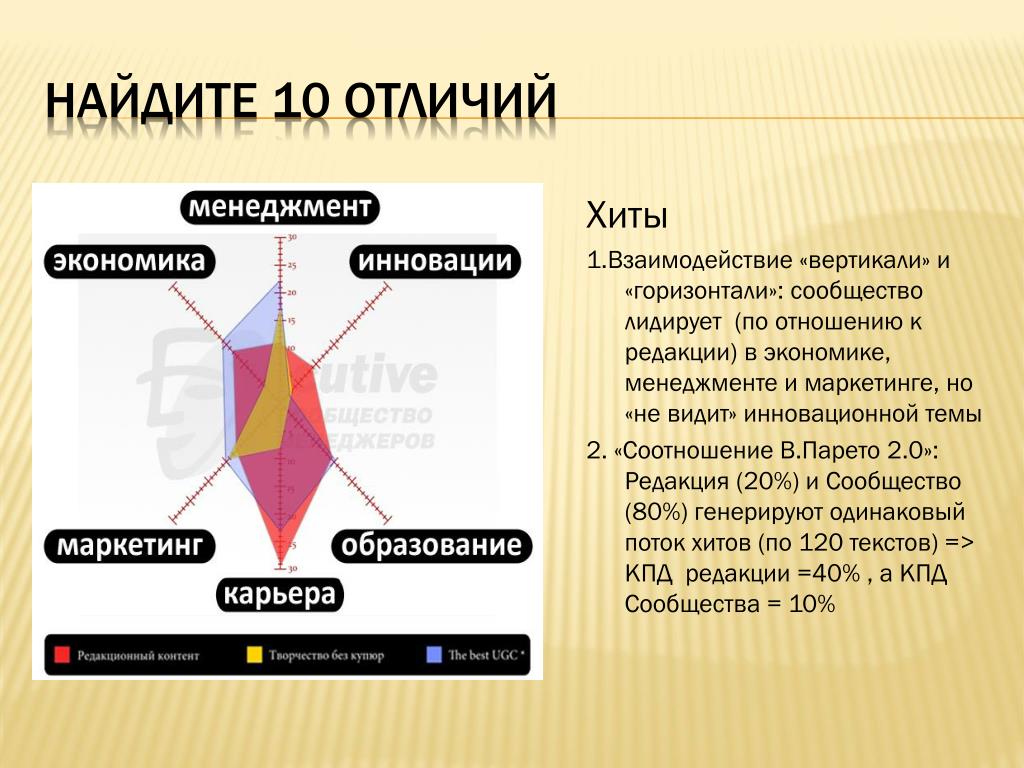 Большое влияние имеют тон и цвет линии по отношению к остальному изображению, а также её повторяемость.

Как и любой приём, линии могут помочь создать или наоборот разрушить образ.

Горизонтальные линии

Горизонталь во многих смыслах служит базовой линией композиции. Это фундаментальная ориентирная линия, самая знакомая из всех, и даже её визуальная тяжесть — это напоминание о том, что горизонтальная поверхность есть держащая основа. Поэтому горизонтальные линии обычно выражают стабильность, вес, мир и спокойствие. Через их ассоциацию с горизонтом они также указывают на дистанцию и широту.

Прямые горизонтальные линии могут играть роль разделительной черты, заставляющей зрителя оставаться снаружи, заглядывая за них.

Горизонтали практически всегда присутствуют в перспективном изображении. Даже беспорядочные скопления объектов с увеличением дистанции превращаются в горизонтальные вереницы предметов, и в конченом итоге — в линии.

Вертикальные линии

Вертикаль — второй основной компонент рамки.
Для единичной вертикали более подходит вертикальный формат. Однако группа вертикальных форм может служить основой горизонтального кадра.

Вертикальная линия обычно является главным компонентом изображения человеческой фигуры или дерева. Её направление совпадает с направлением вектора силы тяжести или противоположно ему.
Без ассоциации с поддерживающей основой, характерной для горизонтальной линии, вертикальная линия обычно в большей степени даёт ощущение скорости и движения — либо вверх, либо вниз.

Видимые отвесно с низкой точки съёмки вертикали при подходящих обстоятельствах словно противостоят зрителю. Изображение содержащее выраженные вертикальные линии как правило вызывает ощущение высоты и значительности.

Несколько вертикальных форм могут вызывать ассоциации с барьером — например, столбы или шеренга людей, стоящих лицом к объективу. В какой-то степени они могут олицетворять силу и власть.

Как и в случае с горизонтальными линиями, здесь очень важно выравнивание. На фотографии и те и другие сразу сопоставляются взглядом с краями рамки, и даже незначительное несоответствие моментально бросается в глаза.

Горизонтальные и вертикальные линии перпендикулярны и действуют как ограничители друг друга, уравновешивая композицию. Также они могут создавать ощущение баланса, так как возникает ассоциация с прямым стоянием, поддерживаемым на плоской поверхности.

Композиция, основанная на вертикальных и горизонтальных линиях вызывает ощущение надёжности, удовлетворения.

Материал возмутительным образом скопирован из:

Майкл Фриман. Дао цифровой фотографии (pdf)
Эксель, Бетдорф и др. Искусство фотографии: сила композиции (pdf)
wikipedia.org: Composition_(visual_arts)

Иллюстрации, на мой взгляд, подобраны не сильно удачно, но общую идею вроде удалось показать.

Добро пожаловать в комментарии, там можно обсудить описание, задания и способности автора 🙂

Также категорически приветствуется обсуждение всего что касается выполнения задания, непонятных моментов и прочего. Это едва ли не главное, ради чего стоит обучаться вместе!

Спасибо за внимание!

Задания к выпуску
Другая сторона практики — пересмотрите любимые работы фотографов и живописцев. Обратите внимание, как используются описанные приёмы. Поделитесь вдохновением с соучастниками 🙂

Горизонталь или вертикаль: какую карьеру выбрать?

Существует два основных вида карьеры: вертикальная и горизонтальная. Сейчас все больше ценятся узкие специалисты, мастера своего дела, которые делают ставку как раз на горизонтальную карьеру, на развитие вглубь. Это золотой фонд компании. За такими сотрудниками охотятся рекрутеры и работодатели. Какую карьеру выбрать вам?
Начнем с определения карьеры. Термин «карьера» происходит от латинского «carrus» (телега, повозка) и итальянского «carriera» (бег, жизненный путь, поприще). Наиболее распространенное толкование слова «карьера» — продвижение вперед в определенной сфере деятельности. Например, получение бóльших полномочий, более высокого статуса, престижа, власти, денег. Под словосочетанием «сделать карьеру» понимается достижение престижного положения в обществе и более высокого уровня дохода.

Вертикаль и горизонталь

Карьера подразумевает разнообразные варианты профессионального роста и продвижения по службе. Горизонтальная карьера (карьера вширь) — это когда человек берет на себя более широкий круг обязанностей и полномочий на своем рабочем месте. Это верный путь к узкому профи, мастеру своего дела. Такие сотрудники сегодня очень высоко ценятся рынком. За ними будущее. Их готовы перекупать, удерживать, развивать, мотивировать.
Часто обязанности работника при горизонтальном перемещении меняются, но должность остается прежней. Иногда у него появляется возможность по совместительству руководить проектом или преподавать. Горизонтальная карьера подразумевает и расширение полномочий, ответственности, повышение статуса, увеличение бонусов и оплаты труда.
Карьера вширь характерна для экспертов, научных сотрудников, консультантов, людей творческих профессий, профильных работников, которые являются лучшими в своей области. Эти специалисты профессионально совершенствуется в рамках своей должности, но кресло начальника в ближайшем будущем они, как правило, занять не стремятся.

В горизонтальной карьере нет других конкурентов, кроме себя вчерашнего. Все остальные — учителя. Когда человек перерастает определенный уровень, он сам становится наставником и передает дальше свой опыт, знания, умения.

Вертикальная карьера

Вертикальная карьера — это движение вверх по служебной лестнице. Здесь карьерный рост настолько очевиден, что порой его отождествляют с самим понятием «карьера». Итак, вот как может выглядеть вертикальная карьера финансиста. Выпускник финансового института работает некоторое время помощником бухгалтера, потом бухгалтером, затем заместителем главного бухгалтера, главным бухгалтером, финансовым директором, заместителем генерального директора, генеральным директором.

Но в то же время молодой человек может, набравшись опыта и накопив клиентскую базу, создать собственную компанию. В идеале вертикальная карьера заканчивается на посту генерального директора (президента) компании. Но в реальном бизнесе редко можно встретить такой тип карьеры в чистом виде.
Движение по вертикали привязано к социуму. У начальника всегда должны быть подчиненные, иначе повышение не имеет смысла. Наличие конкурентов предъявляет к «вертикальному карьеристу» жесткие требования. Стремящийся к вертикальной карьере сотрудник должен наращивать как профессиональные, так и управленческие навыки. Его цель — стать лучшим, а в идеале единственным. Часто вертикальная карьера связана не только с самореализацией, но и с самоутверждением — через социальный статус, власть над подчиненными, материальную обеспеченность. Плохо, когда сама деятельность для человека лишь средство достижения этих благ. Так появляются начальники-самодуры, которые обрушивают свои личные амбиции на головы подчиненных.

Универсальных рецептов не бывает!

Люди, строящие горизонтальную карьеру, составляют золотой фонд компании. Как правило, эти сотрудники любят свою профессию, свое дело, оно им интересно, у них, что называется, горят глаза. Эксперты считают, что за таких узких специалистов и будут бороться работодатели. Перед последними встанет вопрос: как мотивировать такого рода сотрудников, чтобы они остались работать именно в данной компании?
«Как отмечают многие психологические исследования, в наше время, финансовая мотивация стоит не на первом месте, поэтому мотивировать сотрудников можно интересными задачами и проектами, вовлеченностью в процесс развития компании. А для данной вовлеченности в процесс сотрудники должны знать цели, задачи и стратегию компании, и понимать, какой вклад в реализацию этих целей, задач и стратегии вносит каждый из сотрудников. Необходимо помнить о поощрении (не только финансовом) тех сотрудников, которые показали наилучшие результаты в работе.

К тому же, для сотрудников, стремящихся к построению карьеры в компании, важным является понимание того, что необходимо сделать, каких результатов добиться, для того, чтобы перейти на следующую ступень. Поэтому с первых дней работы сотрудники должны понимать систему роста в компании. Да и не стоит забывать про то, что есть у сотрудников интересы и увлечения помимо работы, которые тоже можно и нужно рассматривать как средства мотивации», — комментирует Анастасия Максимова, специалист по работе с персоналом, Иностранное унитарное предприятие «ДИСКОМ», группа фирм CAPAROL
Даже если работодатель не готов платить зарплату выше средней по рынку или организация вынуждена экономить на соцпакете, то можно мотивировать сотрудника различными дополнительными мероприятиями. Это могут быть тимбилдинги, возможность обучения внутри компании, скидки в магазинах и ресторанах, льготное кредитование, новогодние подарки, совместные праздники, возможность интересных командировок, внутренние коммуникации (электронная газета, общие собрания, участие в работе над разными проектами и т.

д.). Еще, как это ни банально, важно не забывать регулярно благодарить людей за хорошо выполненную работу.

Главное — личные ценности

Одному нужна помощь компании в изучении иностранного языка, другой хочет посетить семинар с целью более детального изучения своей специальности, третьему достаточно подарить на рождение ребенка коляску, а четвертый давно мечтал об абонементе в спортивный клуб рядом с домом. Важно, чтобы HR-отдел держал руку на пульсе событий, регулярно выясняя потребности персонала.

Деньги мотивируют всех!

Если есть возможность увеличения зарплаты и улучшения условий труда, то работникам не нужен вертикальный рост. Но желание иметь больше денег и больше возможностей для комфортной жизни есть у каждого. Следует уделять внимание в первую очередь постоянным сотрудникам — тем, кто проработал в компании свыше двух лет. Нужно давать им больше полномочий, возможностей проявить себя.
Итак, если работнику интересно развиваться горизонтально, ставьте перед ним более сложные задачи в рамках его компетенций. Его можно периодически переводить (с его согласия, конечно же) в другой отдел — чтобы глаз не замыливался, чтобы он осваивал новые сферы деятельности.

Кого ценят работодатели?

Кого компания больше ценит, в том числе финансово, — строящих вертикальную или горизонтальную карьеру?

«Компании ценят ответственных и грамотных сотрудников, приносящих прибыль, — считает Анастасия Максимова, специалист по работе с персоналом, Иностранное унитарное предприятие «ДИСКОМ», группа фирм CAPAROL, — А что касается построения карьерной лестницы в компании, то возможны варианты, в зависимости от актуального этапа развития конкретной компании и принятых корпоративных норм и стандартов.
В нашей стране широко представлены и те компании, которые вкладывают время и средства в развитие своих сотрудников, растят топ-менеджмент у себя внутри, и соответственно заинтересованы в лояльных сотрудниках. Но есть и те, кто старается взять сотрудника, который скорее заполнит недостающую функциональную единицу, и не будет стремиться к росту.
Наша компания относится к первому типу компаний: мы вкладываем много средств и времени в обучение и постоянное развитие сотрудников, и заинтересованы в том, чтобы сотрудники росли и строили свою карьерную лестницу в нашей компании. И ценим соответственно и тех, кто строит вертикальную карьеру, и тех, кто хочет развиваться горизонтально, но связывает свою карьеру именно с нашей компанией».
В последнее время рынок приходит к тому, что работодатели готовы платить достойную зарплату и предоставлять бонусы не только топ-менеджменту, но и узким специалистам, которые как раз развиваются горизонтально.
Нацеленные на горизонтальный рост сотрудники стремятся к профессиональному росту, и в силах компании обеспечить их ресурсами: предоставить бóльшую степень свободы, возможность реализовывать новые идеи. Хорошо, если человек будет учить других, использовать свой педагогический и управленческий потенциал.

Определитесь: вертикаль или горизонталь

Когда вы придете устраиваться на работу, вас не должны застать врасплох вопросы о видах карьеры.

Желательно заранее определиться, в какую сторону вы собираетесь развиваться: вширь или в высоту. Именно горизонтальная карьера на определенном этапе вашей профессиональной деятельности может послужить отличным началом к восхождению по вертикали. Опыт, умения, знания приобретаются именно во время работы по специальности. Рынок уже пришел к тому, чтобы платить достойные деньги именно мастерам своего дела. Людей с управленческими навыками и массой бизнес-образований сейчас достаточно, а вот отличных исполнителей, в совершенстве знающих свой продукт, не хватает.
Самое главное — определить для себя, какой путь построения карьеры подходит именно вам. Важно, чтобы он совпадал с вашими истинными потребностями. Ваши профессиональные навыки, знания, опыт — это основа, почва для любого вида карьеры, а главное, это основа профессионального развития. В то время как социального статуса, должности, материальных благ можно лишиться в один момент, ваша профессия будет с вами всегда.

Вертикали и горизонтали в картинах мира Текст научной статьи по специальности «Языкознание и литературоведение»

сажирами вели за собой паровозы.

УЖД временно возводились для военных целей в качестве фронтальных и рокадных железных дорог, перебрасывавших соединения и снабжавших их. Предшественником военно-полевых железных дорог (ВПЖД) с локомотивной тягой были рельсовые пути узкой колеи, на которых применялась конная тяга. Такие пути использовались, в частности, в ходе Русско-Японской войны. В период двух мировых войн противоборствующими сторонами было построено множество облегченных дорог с шириной колеи 600 мм. Большинство ВПЖД перешивались или разбирались после окончания военных действий, но некоторые из них действовали и после войны, проходя через конверсионные процедуры.

Что касается торфовозных узкоколеек, то их основным назначением принято считать перевозку торфа от места, где он добывается, до места погрузки или же к месту сжигания или переработки. Среди основных потребителей торфа в Советском Союзе были тепловые электростанции и химическая промышленность. Одна из причин заката торфовозных узкоколеек — переход энергетических объектов на газ или мазут.

Во многих «непроходимых местах» узкоколейка имела статус единственного средства сообщения для населения. Например, закрытие узкоколейки Тула-Лихвин, где ходило в день пять пар пригородных поездов, не могло не вызвать народный протест. Среди пассажирских узкоколейных дорог на постсоветском пространстве известны: украинская узкоколейка Руд-ница-Гайворон-Ольвиополь с ветвями на Чечельник и Гайсин; Рязань-Тумская линия, проходящая по Ме-

щере; прибалтийская узкоколейная сеть общего пользования, которая вплоть до 1960-х гг. была едва ли не протяженнее широкой [6, с. 170-171].

Важно уточнить оптимальную область применения УЖД. Исследования ученых, подтвержденные опытом работы лесозаготовительных предприятий, показывают, что узкоколейный транспорт наиболее эффективен на крупных и концентрированных лесосырьевых базах при грузообороте от 400 тыс. до 2 млн т и средних расстояниях вывозки от 40 до 200 км [4]. Именно лесная отрасль давала наибольшие возможности для развития УЖД, поскольку строительство новых веток зависело от темпов выработки лесных массивов.

Ускорившийся переход на внутрирегиональные автомобильные грузовые перевозки в 1970-е гг. и кризис промышленного производства в 1990-е гг. нивелировали все преимущества использования УЖД и привели к тому, что протяженность узкоколейных дорог в России резко уменьшилась, причем даже приблизительных статистических данных о современной суммарной протяженности всех узкоколеек страны нет. Среди сохранившихся крупных УЖД на постсоветском пространстве можно назвать Сахалинскую, Алапаев-скую, Кудемскую, Лойгинскую и Апшеронскую узкоколейки.

УЖД в одночасье потеряли значение транспортных капилляров, пронизывавших пространство вблизи хозяйственных объектов, и еще только предстоит оценить роль узкоколейного транспорта в истории развития отдельных регионов.

Статья поступила 09.04.2015 г.

Библиографический список

1. ГОСТ 5865-51-1955. Железные дороги узкоколейные наземные и подземные. Ширина колеи. М.: Изд-во стандартов, 1988. 28 с.

2. Алексеев С.В., Кравченко Ю.М. Узкоколейки — тоже транспортная сеть [Электронный ресурс]. URL: http://tppekb.ru/publications/uzkokoleyki-tozhe-transport/ (30.03.2015).

3. Арсеньев К.К. Энциклопедический словарь Брокгауза и Ефрона: в 86 т. СПб.: Брокгауз-Ефрон, 1902. Т. 34А. 960 с.

4. Берзегов А.П. Надежная узкоколейка [Электронный ресурс]. URL: //moshud.info/ moshud-article/article/nadezhnaja-uzkokoleika (28.03.2015).

5. Бурлев Е.О., Кравченко Ю.М. От колеи до колеи — во-

круг земного шара [Электронный ресурс]. URL: http://tppekb.ru/publications/ot-kolei-do-kolei-vokrug-zemnogo-shara/ (28.03.2015).

6. Вульфов А.Б. Повседневная жизнь российских железных дорог. М: Молодая гвардия, 2007. 496 с.

7. Москалев Л.М. Наши узкоколейные паровозы. М.: Железнодорожное дело, 1997. 408 с.

8. Общий курс железных дорог / под ред. В.Н. Соколова. М.: УМК МПС России, 2002. 296 с.

9. Прохоров А.М. Большая советская энциклопедия: в 30 т. М.: Советская энциклопедия, 1977. Т. 26. 624 с.

10. Сотников Е.А. Железные дороги мира из XIX в XXI век. М.: Транспорт, 1993. 200 с.

УДК 72.03:821.161.1

ВЕРТИКАЛИ И ГОРИЗОНТАЛИ В КАРТИНАХ МИРА

Пензенский государственный университет архитектуры и строительства, 440028, Россия, Пенза, ул. Титова, 28.

Показана роль гравитационных вертикалей и горизонталей в картинах мира в поэзии и прозе А. С. Пушкина. Рассмотрены смыслы, выраженные с их помощью в скитаниях по Крыму, Кавказу и дорогам России. Разобран метафорический вклад привлеченных при этом пространственных элементов, отношений, качеств. Очерчен их идей-

1Стеклова Ирина Алексеевна, кандидат искусствоведения, доцент кафедры «Дизайн и ХПИ», тел.: 89023533543, e-mail: [email protected]

Steklova Irina, Candidate of Art Criticism, Associated Professor, tel.: 89023533543, e-mail: [email protected]

ный диапазон на основании культурных универсалий романтической эпохи. Выдвинуто предположение о том, что вертикали и горизонтали архитектуры предлагают не только понимание о мире, но и объясняют мир собою. Ключевые слова: архитектурное пространство; архитектоника; картина мира; базовые и культурные универсалии; Пушкин.

VERTICALS AND HORIZONTALS IN WORLD VIEWS I. A. Steklova

Penza State University of Architecture and Construction, 28 Titov St., Penza, 440028, Russia.

The article demonstrates the role of gravitational verticals and horizontals in the worldviews of Alexander Pushkin’s poetry and prose. The meanings expressed by means of them are considered in wandering in Crimea, Caucasus and Russian roads. Metaphorical contribution of the brought-in spatial elements, relationships and qualities is analyzed. Their ideological range is outlined on the basis of Romantic era cultural universals. A hypothesis is made that architectural verticals and horizontals provide both world understanding and world explanation through themselves. Keywords: architectural space; architectonics; worldview; basic and cultural universals; Pushkin

Геометрические универсалии миропонимания у А. С. Пушкина преимущественны перед цветовыми, световыми, динамическими и т.п. универсалиями. Через них в абстрактном, природном или архитектурном пространстве постигались, переживались и оценивались все постоянные и переменные явления, попадающие под какую-либо определенность в процессе познания и объяснения. В частности, его картины мира -это прозаические и поэтические модели мироощущения и миропонимания с ортогональным соподчинением несущих и несомых сущностей, в габаритах или бесконечности. Архитектоника этих моделей задает надежность мира, а значит, его расположенность к человеку.

Считается, что решающую роль в пушкинском опыте архитектонического моделирования действительности и в построении картин мира сыграли Крым и Кавказ — приобщение к любимому умом простору, который не подавлял, но, напротив, возвышал [18]. Недаром через пять лет после ссылки поэт добровольно вернется к возможности проникнуть в иерархию законного мироустройства и вскрыть ее послойно: Кавказ подо мною. Один в вышине Стою над снегами у края стремнины: Орел, с отдаленной поднявшись вершины, Парит неподвижно со мной наравне* [8, с. 131] *Здесь и далее выделены курсивом цитаты из текстов А.С. Пушкина, а также слова в значении цитат, приведенных по изданию: Пушкин А.С. Полное собрание сочинений в 10 т. Л.: Наука, 1977-1979.

Поэт стал свидетелем соперничества ортогонально ориентированного простора и предельной тесноты, взлетов и провалов. Горизонтальные расстояния моделировались в положении сверху вниз, что называется, с птичьего полета, и снизу вверх, в виде перспективы с точкой схода, теряющейся в облаках, на древней церкви Цминда Самеба. Равновесие грандиозных контрастов по вертикали и горизонтали оценивалось как неподдельная гармония: Высоко над семьею гор, Казбек, твой царственный шатер Сияет вечными лучами. Твой монастырь за облаками, Как в небе реющий ковчег, Парит, чуть видный, над горами [11, с. 134].

В отточенной самоорганизации горных ландшафтов, по мысли А. И. Каплуна, выявлены все архитектонические принципы, присущие большому зодчеству, более того, целеполагания зодчества: здесь нет «конфликта формы» [2, а 187] между массой и пространством, неодолимого и в самом совершенном рукотворном решении. Этим, например, покоряла многих художников громадная шапка Аю-дага (рис. 1), органично доминирующая в природе: «увидел я картину пленительную: разноцветные горы сияли; плоские кровли хижин татарских издали казались ульями, прилепленными к горам; тополи, как зеленые колонны, стройно возвышались между ими; справа огромный Аю-даг… и кругом это синее, чистое небо, и светлое море, и блеск и воздух полуденный…» [12, с. 429].

Бесконфликтные формы, архитектурообразно структурированные стихией, замечались поэтом и словесно, и графически. Так, нарисованный на полях первой главы «Евгения Онегина» арочный проем в горе признан Золотыми воротами Карадага. С мифом о других воротах связывалось происхождение названия Дарьяльского ущелья: «Против Дариала на крутой скале видны развалины крепости. Предание гласит, что в ней скрывалась какая-то царица Дария, давшая имя свое ущелию: сказка. Дариал на древнем персидском языке значит ворота» [13, с. 441]. Архитектонические усилия дикой природы вдохновили не одного русского художника и отразились в народном наречии, мудрости которого стоило доверять (рис. 2). Ходила молва, будто выразительное сужение Дарья-льского ущелья использовалось когда-то функционально, и в готовые каменные ворота были вмонтированы для защиты вторые — деревянные, окованные железом:

Притек сатрап к ущельям горным И зрит: их узкие врата Замком замкнуты непокорным; Стеной, как поясом узорным, Препоясалась высота. И, над тесниной торжествуя, Как муж на страже, в тишине Стоит, белеясь, Ветилуя В недостижимой вышине [10, с. 326].

Рис. 1. К.Ф. Кюгельген. Крым. Гурфуз. 1824 г.

Рис. 2. Н.Г. Чернецов. Дарьяльское ущелье. 1832 г.

О раскрепощении творчества Пушкина под влиянием пограничных ландшафтов писал еще Н. В. Гоголь. Считается, что бесконфликтно контрастирующие формы Крыма и Кавказа, архитектонически недосягаемые для городской цивилизации, стали рубежами не только пленения, но и внутреннего освобождения поэта. Именно в их совершенной, ничем не стесненной архитектонике горизонтальность простора и вертикальная шкала как кратчайшая связь с вольной вышиной получили пожизненное преимущество в его оценочных суждениях. В определенном смысле, он так и не вернулся из мира абсолютной свободы, являющейся утопическим кумиром эпохи. Положение об обретенной в горах потребности в вертикальном приращении пространства с бескорыстной экспансией горизонтального — общее место академической науки

в осмыслении метафор поэта. Их попадание в объятия романтизма сохраняет понятийную притягательность, заражая ответной метафоричностью даже критику: «После плоской «метафизической горизонтали» вольтерьянства Кавказ (в два этапа — 1820, 1829) дал ему объем: своей природой, «дикими» нравами, бурлящей жизнью, идущей по иным нормам. Кавказ дал ему вертикаль… И он НА деле убедился в том, что существует высота. После этого он снова оказался в горизонтальном мире — но это была лишь в физическом смысле горизонталь: Россия, ширь, воля. И он, пришедший туда уже новым, другим, вдруг увидел -тоже высоту, но не физическую. После этого появился шестикрылый серафим» [3, с. 384].

Несмотря на то, что восприятие измерений, ориентированных по горизонтали и вертикали, специально исследуется эстетикой, соотнесение поэтики пушкинских творений с горизонталью и вертикалью «в физическом смысле» обречено на клеймо буквализма. Тем более, если таковые взяты не в природе, а в вульгарной рукотворности. Однако независимые умы первой половины XIX века подобных предрассудков не признавали: «Многие <…> подумают, что не всякий и не везде имеет право говорить языком высшей истины — я не такого мнения. Истина, как добро Мольера, там и берется, где попадается» [14, с. 508]. В картинах с объектами, вытянутыми вверх, поднятыми на высоту или увиденными с еще большей высоты, проявлялось особое парение духа, идейное укрупнение, перекрывающее прочие, физически и семантически пониженные обстоятельства места: «он…проникает в глубину пирамид, пускается в пустыню, оживленную черными шатрами бедуинов и верблюдами караванов, вступает в обетованную землю, наконец с высоты вдруг видит Иерусалим…» [16, с. 181].

Поскольку среднерусскому раздолью остроты Крыма и Кавказа не хватало, вертикальные перепады акцентировались здесь особо. Причем не в статичных построениях, а в кадрах кинематографического качества, в динамике подвижных картин. Проехав тридцать четыре тысячи километров по дорогам страны, А.С. Пушкин старался ухватить геометрию ее видоизменяющейся протяженности, понять, чем она собирается на самом деле, требуя «другой мысли, другой формулы, как мысли и формулы, выведенные Гизо-том из истории христианского Запада» [4, с. 100]. Среди сохранившихся рисунков поэта есть несколько дорожных пейзажей, сделанных с натуры и по памяти [19]. На большинстве из них подчеркнута волнообраз-ность рельефа, увенчанная контурами обобщенных поселений, отдельных изб, церквей с колокольнями, господских домов в виде периптеров с треугольными фронтонами и т.п. (рис. 3, 4) Ровно тем же помечались и умозрительные пространства: Господский дом уединенный, Горой от ветров огражденный, Стоял над речкою. Вдали Пред ним пестрели и цвели Луга и нивы золотые… [6, с. 31].

Рис. 3. А.С. Пушкин. Сельский пейзаж. Ноябрь 1833 г.

Рис. 4. А.С. Пушкин. Пейзаж с рекой

Несколько героев поэта получили возможность переоценить смысл собственной жизни на местности с крутым холмом, откуда все может развернуться. Наиболее емкие характеристики давались с самых высоких точек обзора:

Шла, шла. И вдруг перед собою С холма господский видит дом, Селенье, рощу под холмом И сад над светлою рекою [6, с. 126]. Разные дома деревенских жителей либо ставились на возвышенностях, либо с возвышенностей раскрывались. Так, для лучшего кругового обзора был поднят дом Нулиных. Старинный дом на горе с садом и озером возникнет в «Романе в письмах». Сразу три усадьбы в сложном рельефе появятся в повести «Дубровский», где сначала покажется новая пятиглавая церковь со старинной колокольней и огромный каменный дом с зеленой кровлей, потом жилище во вкусе английских замков с видом на Волгу, за которой несколько деревень оживляли окрестность, и, наконец, «березовая роща и влево на открытом месте серенький домик с красной кровлею» [5, с. 157]. Вид третьего дома, да и всей усадьбы, повторял изображение из «Истории села Горюхина», начатой ранее. Намеченный в плане горюхинской летописи пункт Число жителей. Архитектура. Церковь деревянная был раскрыт здесь, и деревянная церковь выросла рядом с кладбищем, осененном старыми липами. Буквальный повтор текста в повестях, сочиненных с

трехлетним перерывом, обнаруживает личностную интонацию автора, выделившего серенький домик красной, почти кровной кровлей.

Черты скромных родительских усадеб и их окрестностей: холмистого Михайловского и равнинного Болдина — перешли в произведения поэта. В житейском переходе от первого ко второму произошло естественное обмельчание его романтических представлений:

Иные нужны мне картины: Люблю песчаный косогор, Перед избушкой две рябины, Калитку, сломанный забор, На небе серенькие тучи… [6, с. 174]. Картины мира с равнинной архитектоникой показали новое отношение к выразительности пространства, независимого от сильных доминант ни в ландшафте, ни в архитектуре: «Я глядел во все стороны, ожидая увидеть грозные бастионы, башни и вал; но ничего не видал, кроме деревушки, окруженной бревенчатым забором. С одной стороны стояли три или четыре скирда сена, полузанесенные снегом; с другой скривившаяся мельница, с лубочными крыльями, лениво опущенными. „Где же крепость?»» [9, с. 275]. В степной унылости Болдина, без привычного сада и цветников, радовали лишь роща, прозванная Лучинником, и пруд. Впечатлениями от подобного пейзажа делился прапорщик из неоконченных «Записок молодого человека»: «Я сел под окно. Виду

Рис. 5. П.А. Александров, с оригинала И.С. Иванова. Михайловское. 1837 г.

никакого. Тесный ряд однообразных изб, прислоненных одна к другой.Я пошел по большой дороге -справа тощий озимь, слева кустарник и болото. Кругом плоское пространство. Навстречу одни полосатые версты. В небесах медленное солнце, кое-где облако. Какая скука!» [7, с. 386]. Только и пустырь с вкраплениями безликих построек, физически приближаясь, становился созвучным пронзительной русской безбрежности:

Смотри, какой здесь вид: избушек ряд убогий, За ними чернозем, равнины скат отлогий, Над ними серых туч густая полоса. Где нивы светлые? где темные леса? Где речка? На дворе у низкого забора Два бедных деревца стоят в отраду взора, Два только деревца. [17, с. 179].

Рис. 6. Д.О. Аткинсон. Русская деревня

Рис. 7. А. Мейерберг. Деревня Зимогоры. Из книги «Путешествие в Московию»

Эстетика в низких, распластанных ландшафтах истиралась за ненадобностью. Даже цвет в эту трех-плановую перспективу добавлялся один — серый, правда, в максимальной тональной растяжке. Монохромное плоское пространство цеплялось за деревце, за полосатые столбы и в прозаической иронии, и в поэтической риторике, и в публицистических выводах аналитического характера: «Наружный вид русской избы мало переменился со времен Мейерберга. Посмотрите на рисунки, присовокупленные к его «Путешествию». Ничто так не похоже на русскую деревню в 1662 году, как русская деревня в 1833 году. Изба, мельница, забор — даже эта елка, это печальное тавро северной природы…» [13, с. 198]. Воля к развитию действия, прописанного в ландшафтах родины, усиливалась и этими стержнями. Онтологические и метафизические смыслы, поднимаемые на высоту, нанизываемые на вертикали и разворачиваемые по горизонтали, в пластике поверхностей и объемов, тем же неизбежно нагружали и самое незамысловатое архитектурное овеществление.

Дистанцируясь от допусков праязыка пластических искусств в эволюции эстетических воззрений, нельзя не учитывать использования вертикалей и горизонталей для архитектонического моделирования действительности как глубинной основы миропонимания. Даже дилетантское объяснение архитектуры, как, впрочем, и ее профессиональный комментарий, а также проектирование и строительство, зиждется на них, обозначаемых так или иначе. Гравитационная вертикаль и горизонталь, высота и широта в неколебимых декартовых осях несут и массы, и пустоты объектов и образуют в них, в видении А. В. Бокова, швы, линии деления, расчленения, способные «выступать независимо в качестве формопорождающих обстоятельств» [1, с. 19].

Русское самосознание ждало от мира архитектонической внятности и надежности. В пушкинских картинах мира эта потребность удовлетворялась посредством гармонизации геометрических универсалий, в первую очередь вертикализма и горизонтальности.

При этом с горизонтальным развитием связывался простор, а с вертикальным — свобода. Некоторое преимущество у автора имели абстрактные или архитектурно облеченные вертикали, наделяемые этическим и даже нравственным содержанием. Понимание

нравственности в свободе удерживалось ими настолько убедительно, насколько надежно организовывали пространство их реальные прототипы.

Статья поступила 25.05.2015 г.

Библиографический список

1. Боков А.В. Геометрические универсалии архитектуры в картине мира: автореф. … докт. архитектуры. М.: НИИТАГ, 1995. 36 с.

2. Каплун А.И. Стиль и архитектура. М.: Стройиздат, 1984. 232 с.

3. Непомнящий В.Я. Поэзия и судьба. Книга о Пушкине. М.: Московский городской фонд поддержки школьного книгоиздания, 1999. 480 с.

4. Пушкин А.С. Второй том «Истории русского народа» Полевого. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VII. С. 97-100.

5. Пушкин А.С. Дубровский. ПСС в 10 т. Л.: Наука, 19771979. Т. VI. С. 142-209.

6. Пушкин А.С. Евгений Онегин. ПСС в 10 т. Л.: Наука, 19771979. Т. V. С. 5-184.

7. Пушкин А. С. Записки молодого человека. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VI. С. 385-387.

8. Пушкин А.С. Кавказ. ПСС в 10 т. Л.: Наука, 1977. Т. III. С. 131.

9. Пушкин А.С. Капитанская дочка. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VI. С. 258-370.

10. Пушкин А.С. Когда владыка ассирийский. ПСС в 10 т. Л.: Наука, 1977. Т. III. С. 326.

11. Пушкин А.С. Монастырь на Кавказе. ПСС в 10 т. Л.: Наука, 1977. Т. III. С. 134.

12. Пушкин А.С. Отрывок из письма к Д. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VI. С. 429-431.

13. Пушкин А.С. Путешествие в Арзрум. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VI. С. 432-484.

14. Пушкин А.С. Из ранних редакций. Путешествие в Арзрум. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VI. С. 505-510.

15. Пушкин А.С. Путешествие из Москвы в Петербург. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VII. С. 184-249.

16. Пушкин А.С. «Путешествие к св. местам» А. Н. Муравьева. ПСС в 10 т. Л.: Наука, 1977-1979. Т. VII. С. 180.

17. Пушкин А.С. Румяный критик мой, насмешник толстопузый. ПСС в 10 т. Л.: Наука, 1977. Т. III. С. 179.

18. Стеклова И.А. Архитектура в поэтической картине мира // Современные проблемы науки и образования. [Электронный ресурс]. 2014. № 4 URL: www.science-education.ru/118-13422 (28.02.2015).

19. Стеклова И.А. Архитектура в текстах и графике Пушкина // Архитектон: известия вузов. [Электронный ресурс]. 2011. № 34. URL: // http://archvuz.ru/2011 _2/13 (22.02.2015).

УДК 378.14

ПОВЫШЕНИЕ КАЧЕСТВА ПОДГОТОВКИ СТУДЕНТОВ НА ОСНОВЕ СОВРЕМЕННЫХ ОБРАЗОВАТЕЛЬНЫХ МОДЕЛЕЙ

Северо-Кавказский горно-металлургический институт (Государственный технологический университет), 362000, Россия, г. Владикавказ, ул. Николаева, 44.

Рассматриваются вопросы повышения качества подготовки студентов на основе современных образовательных моделей: демонстрационной модели, программированного обучения, информационно-справочной модели, модели конструирования знаний. Особое внимание уделяется разрабатываемой авторами структурно-функциональной модели обучения, включающей педагога, персональный компьютер (ПК), интернет-ресурсы, учебную книгу и технические средства обучения (ТСО).

Ключевые слова: модели обучения; качество подготовки студентов; структурно-функциональная модель обучения.

STUDENT TRAINING QUALITY IMPROVEMENT ON THE BASIS OF MODERN EDUCATIONAL MODELS N.A. Tsgoeva

North-Caucasian Mining and Metallurgical Institute (State Technological University), 44 Nikolaev St., Vladikavkaz, Republic of North Ossetia-Alania, 362000.

The article covers the issues of improving the quality of training students on the basis of modern learning models: a demonstration model, a model of computer-assisted learning, a reference information model, a model of knowledge structuring. Special attention is paid to a structural and functional model of learning including a teacher, a personal computer (PC), Internet resources, a student’s book and technical training aids (TTA). Keywords: learning models; quality of training students; structural and functional learning model.

Качество образования в современных условиях является важной характеристикой, которая определяет конкурентоспособность как отдельных учебных за-

ведений, так и национальных систем образования в целом. Центральное место в реформировании образования занимает обеспечение и повышение качества

1Цгоева Наталья Анатольевна, ассистент кафедры «Информационные системы в экономике», тел.: 89284983028, e-mail: [email protected]

Tsgoeva Natalia, Assistant Professor of the Department of Information Systems in Economy, tel.: 89284983028, e-mail: [email protected]

Вертикаль и Горизонталь Андрея Тарковского » Философия вертикали+горизонтали. Константин Рылёв. Блог-книга на Peremeny.ru

Начало – здесь. Предыдущее – здесь.

На примере анализа фильмов Тарковского как одного из самых сложных явлений искусства я хотел показать принципы работы Вертикали+Горизонтали. Разберемся пока поподробнее с самими понятиями.

Вертикаль

Вертикаль – связь с Космосом, эта категория – вне времени (даже в учебниках по физике за шестой класс в стандартной системе координат прямая времени – горизонтальная; если время расположить по вертикали, с ним начнет твориться то, о чем предупреждал старина Эйнштейн).

Вертикаль чувствуется в состоянии статики, нужно остановить время. Ближе к этому состоянию – поэзия. В ней внимание уделяется деталям, красоте рисунка.

Вот пример соотношения статики и динамики. Человек едет на велосипеде. Он – в потоке автомобилей, его захватывает движение, он наслаждается ощущением скорости. Но различает он только дорогу и машины. Вот человек резко съезжает с шоссе к реке. Застыв, он вдруг видит, как на воде корабликами курсируют крошечные травинки, а под ними шастают мальки. Перед его носом в любовном танце замерли стрекозы, а наверху величественно планирует ворона, воображая себя орлом. Все это можно заметить только в статическом состоянии.

Хорошие поэты, такие как Флобер, редко бывают общественно активны, им ближе созерцательное отношение к жизни. В «Мадам Бовари» так подробно и ярко описаны сотни деталей Нормандии, что эту часть планеты представляешь как живую. Но динамичность этой литературной вселенной придают поступки уважаемой Бовари. Если бы не ее страсть к мужчинам и деньгам, произведение бы провисло. Основой для романа послужило реальное судебное разбирательство, происходившее в Руане. В других книгах мастера не чувствуется такого мощного волевого вектора. Сказалось безвылазное домашнее времяпрепровождение великого писателя. Его ученик Мопассан в силу бойкого темперамента почти идеально сочетал в своих произведениях динамику и статику, детали и сюжет, поэзию и прозу, Вертикаль и Горизонталь.

К Вертикали относятся гуманитарная область, образное мышление, за которое отвечает правое полушарие мозга. Категории Вертикали – дух, интуиция.

Из сторон света ей соответствует восток. (Основатели всех ведущих мировых религий – уроженцы Востока.) Из стихий – огонь.

Горизонталь

Горизонталь – волевые, решительные поступки, время, «завоевательная» власть, направленная на увеличение масштаба влияния. Деньги, разумеется. Так поступают американцы: можно снять в Голливуде любую ерунду, но благодаря мощному промоушену заставить посмотреть ее пять материков.

Пример «горизонтальной» силы – татаро-монгольские завоевания. Однако татары не сохранили влияния, их философия и религиозные представления работали только в динамике. Кочевники – что с них взять? Любая же добротно организованная империя сразу пытается навязать покоренным свою религию и идеологию. У Золотой Орды были только разные формы шаманизма (исламизация наступила позднее).

Горизонталь – логика, «здравый смысл», точные науки, за которые несет ответственность левое полушарие головного мозга.

Сторона света – запад. Фундаментальные открытия в точных дисциплинах за европейцами. Чисто горизонтальное мышление наиболее явно демонстрируют США.

Тут же и женская, материнская ипостась: размножение и сохранение (что порой подразумевает: своим – все, чужим – ничего).

Из определяющих стихий – вода.

Стремление к идеалу

Точка Пересечения – Бог.

В любом человеке, разумеется, присутствуют сочетание и взаимодействие макро- и микрокосма, Космоса и Земли, мужского и женского начал, Востока и Запада, Вертикали и Горизонтали. Идеальный вариант – поровну. То есть крест. Ближе всего к Богу – дети. Отец (Вертикаль), мать (Горизонталь), маленькие человечки и рождаются от этого союза, а значит, они в начале своего пути, ближе к Точке Пересечения, к Богу. Отсюда утверждение, что «все дети гениальны». Они еще не выявили собственные способности и не закрепили их, дабы занять в социальной сетке свое место: либо стать «горизонтальным» бухгалтером, либо «вертикальным» священником.

Гениальные художники пытаются совместить внутри себя Вертикаль и Горизонталь, сфокусировать их в одной точке, а затем перенести на полотно. Когда это случается, рождается «Джоконда».

Леонардо, кстати, как никто демонстрирует отказ от мужского и женского начал: юноши и девушки на его картинах похожи. Причем, судя по всему, все они смахивают к тому же на самого великого флорентийца, который, по-видимому, бессознательно наделял их своими чертами. Для него, как для божества (или ребенка), пол модели уже не имел решающего значения (Фрейд, конечно, свой анализ творчества Леонардо свел к сексуальным отклонениям).

Продолжение

купить книгу можно здесь.

Рубрики: I. ФИЛОСОФИЯ ВЕРТИКАЛИ + ГОРИЗОНТАЛИ, Вертикаль и Горизонталь Андрея Тарковского | Оставить комментарий »

На Главную блог-книги «Философия Вертикали+Горизонтали»

Вертикали и горизонтали

Выставка «Вертикаль – Горизонталь: Рихард Пауль Лозе – Владимир Андреенков» в Музее архитектуры им. Щусева. 25.09 – 4.10.2019

Государственный музей архитектуры имени А.В. Щусева, фонд Рихарда Пауля Лозе и фонд поддержки современного искусства Надежды Брыкиной проводят выставку «Вертикаль – Горизонталь: Рихард Пауль Лозе – Владимир Андреенков». Оригинальный проект приурочен к дате 45-летия встречи представителей двух разных художественных направлений – швейцарца Рихарда Пауля Лозе (Richard Paul Lohse, 1902–1988) и советского нонконформиста Владимира Андреенкова (1930).

Точка соприкосновения творчества двух художников – серии работ «Горизонтали» и «Вертикали», созданные ими в 1970-е годы в Швейцарии и СССР. Несмотря на сходство живописной манеры, художественная интерпретация у авторов была разной. Как художник, Р. Лозе обосновывал свои методы в текстах и вычислениях, В. Андреенков же «подходил к своим вертикалям на духовно-интуитивном уровне».

Лозе впервые увидел работы Андреенкова, на выставке в цюрихской Galerie Renee Ziegler, и это стало важным этапом в творческой жизни двух художников. Лично они познакомились в Москве 13 августа 1974 года. Тогда подобное событие воспринималось как встреча представителей двух разных миров, но в которых, несмотря на различия, существуют общие художественные процессы. Между художниками, во многом благодаря их схожим представлениям об искусстве, завязалась дружба. К сожалению, в связи с наличием политических, экономических и языковых преград, им не удалось полноценно поддерживать личное общение.

Посетители выставки «Вертикаль – Горизонталь: Рихард Пауль Лозе – Владимир Андреенков могут по-своему продолжить и интерпретировать разговор художников Андреенкова и Лозе с помощью их работ.

Владимир Емельянович Андреенков – художник советского неофициального искусства второй половины XX века. Его абстрактные произведения, композиционно выверенные геометрические миры, что называется, наследуют русскому авангарду. Встреча в 1974 году с Рихардом Паулем Лозе подтвердила Владимиру Андреенкову, что он «не одинок в своих творческих взглядах и идеях». К личной «математике» и цветовой палитре работ Лозе Андреенков сразу проникся глубоким уважением. Значительное влияние на Владимира Андреенкова оказала подаренная швейцарским художником монография «Рихард Пауль Лозе: модульные и последовательные построения» Ойгена Гомрингера. «В искусственной культурной изоляции книга стала доказательством того, что он находится на верном пути; что существуют люди, которым близко его искусство и которые способны его понять». Художник уделяет много внимания и усилий, поиску «идеальных пропорций, что сближает творчество с музыкальной теорией».

Швейцарский художник Рихард Пауль Лозе – участник направления «конкретного искусства» в рамках авангардной живописи. Своим творчеством, текстами, издательской деятельностью (он был главным редактором журнала «Bauen + Wohnen») Лозе оказал заметное влияние на художественные сообщества в Швейцарии и Европе. Наряду с известными художниками Тео ван Дусбургом, Соней Делоне; Питом Мондрианом он развивал принципы конкретного искусства для создания арт-объектов предназначенных для разнообразного круга «ценителей и покупателей».

Richard Paul Lohse. 15 systematic color series. 1950/62
Открытие выставки «Вертикаль. Горизонталь»
Владимир Андреенков. 4 красных вертикали. 1984/2002
Владимир Андреенков. Созвучия No43. 1991
Владимир Андреенков. Созвучия No44. 1991
Владимир Андреенков. Созвучия No45. 1991
Владимир Андреенков. Созвучия No46.
1991
Владимир Андреенков. Две голубые вертикали No1. 1971
Владимир Андреенков. Две голубые вертикали No2. 1971
Владимир Андреенков. Две голубые вертикали No3. 1971
Владимир Андреенков. Две вертикали 1971-2002
Владимир Андреенков. Красная вертикаль 1972-2002
Richard Paul Lohse. Interpenetration of two color progressions
Richard Paul Lohse. Interpenetration of two color progressions
Richard Paul Lohse. Progression from yellow to violet
Richard Paul Lohse. Interpenetration of five color progressions
Richard Paul Lohse. Interpenetration of four color progressions
Richard Paul Lohse.
Interpenetration of five color progressions
Richard Paul Lohse. Interpenetration of four color progressions
Richard Paul Lohse. Interpenetration of four color progressions
Richard Paul Lohse. Interpenetration of five color progressions
Владимир Андреенков. Вариации на тему пространства. 1970
Владимир Андреенков. Вертикали. 1972
Владимир Андреенков на открытии выставки

Возврат к списку

Выравнивание текста или настройка границ в текстовом поле

Word 2016 для Mac Word для Mac 2011 Еще…Меньше

В Word текст надписи можно выравнивать по вертикали и по горизонтали, а также настраивать ширину полей. Горизонтальное выравнивание определяет расположение левого и правого краев абзаца между полями, а вертикальное — размещение текста между верхней и нижней границами.

Выравнивание текста по горизонтали

В надписи выделите текст, для которого нужно изменить выравнивание по горизонтали.
На вкладке Главная выберите нужный вариант выравнивания .

Выравнивание текста по вертикали

Вы можете выровнять весть текст в надписи по ее верхнему или нижнему краю либо по центру.

org/ListItem»>
Щелкните внешнюю границу надписи, чтобы выделить ее.
На вкладке Формат фигуры щелкните Область форматирования.
Откройте вкладку Параметры фигуры, если она еще не выбрана.
Щелкните значок надписи и выберите пункт Надпись.
Выберите По верхнему краю, По середине или По нижнему краю из раскрывающегося списка Выравнивание по вертикали.

Настройка полей надписи

Щелкните внешнюю границу надписи, чтобы выделить ее.
На вкладке Формат фигуры щелкните Область форматирования.
Откройте вкладку Параметры фигуры, если она еще не выбрана.
org/ListItem»>
Щелкните значок надписи и выберите пункт Надпись.
Вы можете настроить поля слева, справа, сверху и снизу.

Важно: Microsoft Office для Mac 2011 больше не поддерживается. Перейдите на Microsoft 365, чтобы работать удаленно с любого устройства и продолжать получать поддержку.

Обновить

Выравнивание текста по горизонтали

В надписи выделите текст, для которого нужно изменить выравнивание по горизонтали.
На вкладке Главная в области Абзацвыберите нужный вариант выравнивания .

Выравнивание текста по вертикали

Вы можете выровнять весть текст в надписи по ее верхнему или нижнему краю либо по центру.

Щелкните внешнюю границу надписи, чтобы выделить ее.
Перейдите на вкладку Формат (сиреневую контекстную вкладку, которая появляется рядом с вкладкой Главная), а затем в области Текстовое поле щелкните Изменить выравнивание текста внутри .
Выберите требуемый вариант выравнивания.

Настройка полей надписи

Щелкните внешнюю границу надписи, чтобы выделить ее.
В меню Формат выберите пункт Фигура.
В левой области диалогового окна Формат фигуры нажмите кнопку Текстовое поле.
В разделе Внутренние поля настройте параметры расстояния между текстом и внешней границей надписи.

Выравнивание объектов

Настройка обтекания текстом объектов

горизонтальных и вертикальных линий | Purplemath

Наклон и формулаПар. & Перп. Lines

Purplemath

Давайте снова рассмотрим два уравнения, которые мы сделали сначала на предыдущей странице, и сравним уравнения линий с их значениями наклона.

Уравнение первой линии было y = ( ² / ₃ ) x − 4, а наклон линии был м = ² / 3_1.

Уравнение второй строки было y = -2 x + 3, а наклон линии составил м = -2.

В обоих случаях число, умноженное на переменную x , также было значением наклона этой линии. Это соотношение всегда выполняется: если уравнение прямой имеет вид « y =», то число, умноженное на x , является значением уклона м .

Содержание продолжается ниже

MathHelp.com

Параллельные и перпендикулярные линии

Это соотношение станет очень важным, когда вы начнете работать с уравнениями прямых.

Теперь давайте рассмотрим эти два уравнения и их графиков .

Для первого уравнения, y = (² / ₃) x − 4, уклон составил м = ² / ₃, положительное число. График выглядел так:

Обратите внимание, как линия, когда мы двигаемся слева направо вдоль x — ось, направленная вверх к верхней части чертежа; технически линия представляет собой «возрастающую» линию. И… наклон был положительным.

Это соотношение всегда верно: если линия возрастает, то ее наклон будет положительным; а если наклон линии положительный, то ее график будет возрастающим.

Для второй линии y = -2 x + 3, уклон составил м = -2, отрицательное число. График выглядел так:

Обратите внимание, как линия, когда мы двигаемся слева направо по оси x , смещается вниз к нижней части рисунка; технически линия представляет собой «убывающую» линию. И… склон был отрицательным.

Это соотношение всегда верно: если линия убывает, то ее наклон будет отрицательным; а если наклон линии отрицателен, то ее график будет убывающим.

Эта связь между знаком на наклоне и направлением графика линии может помочь вам проверить ваши расчеты: если вы вычисляете наклон как отрицательное, но вы можете видеть из графика уравнения, что линия на самом деле увеличивается (поэтому наклон должен быть положительным), тогда вы знаете, что вам нужно переделать свои расчеты. Знание об этой связи может сэкономить вам баллы на тесте, потому что это позволит вам проверить свою работу перед вы сдаете его.

Итак, теперь мы знаем: возрастающие линии имеют положительный наклон, а убывающие линии имеют отрицательный наклон. Имея это в виду, рассмотрим следующую горизонтальную линию:

y = 4

Ее график показан ниже:

Горизонтальная линия направлена вверх; то есть это возрастающая линия? Нет, поэтому его наклон не может быть положительным. Горизонтальная линия направлена вниз; то есть это убывающая линия? Нет, поэтому его наклон не может быть отрицательным. Какое число не является ни положительным, ни отрицательным?

Ноль!

Таким образом, наклон этой (и любой другой) горизонтальной линии логически должен быть равен нулю. Проведем расчеты, чтобы убедиться в этом. Используя (произвольные) точки на линии (−3, 4) и (5, 4), наклон вычисляется как:

Это соотношение всегда выполняется: нулевой наклон означает, что линия горизонтальна, а горизонтальная линия означает, что вы получите нулевой наклон.

(Кстати, все горизонтальные линии имеют вид « y = некоторое число», а уравнение « y = некоторое число» всегда отображается в виде горизонтальной линии.)

Теперь рассмотрим следующую вертикальную линию:

x = 4

График показан ниже .

Вертикальная линия идет вверх с одного конца? Ну да, вроде. Так что, может быть, наклон будет положительным…? Вертикальная линия идет вниз с другого конца? Ну, опять вроде как Так что, возможно, наклон будет отрицательным…?0009 оба положительные и отрицательные? Неа.

Вердикт: вертикальные линии НЕТ НАКЛОНА. Концепция наклона просто не работает для вертикальных линий. Наклон вертикальной линии не существует , а не !

Давайте проведем расчеты, чтобы подтвердить логику. Из графика линии я буду использовать (произвольно) точки (4, 5) и (4, −3). Тогда наклон равен:

Мы не можем делить на ноль, поэтому, конечно, это значение наклона «не определено».

Это соотношение верно всегда: вертикальная линия не имеет наклона, а «наклон не определен» или «линия не имеет наклона» означает, что линия вертикальна.

(Кстати, все вертикальные линии имеют вид « x = некоторое число», а « x = некоторое число» означает, что линия вертикальна. Каждый раз, когда ваша линия включает неопределенный наклон, линия вертикальной; и каждый раз, когда линия вертикальная, вы закончите делением на ноль, если попытаетесь вычислить наклон.)

Предупреждение: очень часто путают эти два типа линий и их наклоны, но они очень разные.

Как «горизонтальный» совсем не то же самое, что «вертикальный», так и «нулевой наклон» совсем не то же самое, что «без наклона».

Точно так же, как «Z» (с двумя горизонтальными линиями) не то же самое, что «N» (с двумя вертикальными линиями), так и «Нулевой» наклон (для горизонтальной линии) не то же самое, что » Нет» наклона (для вертикальной линии).

Число «ноль» существует, поэтому горизонтальные линии действительно имеют наклон. Но вертикальные линии не имеют наклона; «наклон» просто не имеет никакого значения для вертикальных линий.

Очень часто тесты содержат вопросы, касающиеся горизонталей и вертикалей. Не путайте их!

URL: https://www.purplemath.com/modules/slope2.htm

Страница 1 Страница 3

ORCCA Горизонтальные, вертикальные, параллельные и перпендикулярные линии

Цели: Содержание курса PCC и руководство по результатам

Месяц 60 CCOG 4.4
Месяц 60 CCOG 5.3
Месяц 60 CCOG 6.7
Месяц 60 CCOG 7,5

Рисунок 3.8.1. Альтернативные видео-уроки

Уравнения горизонтальных и вертикальных прямых отличают их от других линейных уравнений настолько, что заслуживают специального исследования. Кроме того, пары прямых, параллельных или перпендикулярных друг другу, обладают интересными особенностями и свойствами. В этом разделе рассматриваются геометрические особенности этих типов линий.

epspdfpngsvgtex

Рисунок 3.8.2. Горизонтальная линия

epspdfpngsvgtex

Рисунок 3.8.3. Вертикальная линия

epspdfpngsvgtex

Рисунок 3.8.4. Две параллельные линии

epspdfpngsvgtex

Рисунок 3.8.5. Две перпендикулярные линии

Подраздел 3.8.1 Горизонтальные линии и вертикальные линии

В разделе 3.7 мы узнали, что все строки можно записать в стандартной форме (3.7.1). Когда $A$ или $B$ равно $0\text{,}$, мы получаем горизонтальную или вертикальную линию, как мы скоро увидим. Давайте возьмем линейное уравнение стандартной формы, $Ax+Bx=C\text{,}$ и по одному пусть $A=0$ и $B=0$ и упростим каждое уравнение.

\начать{выровнять*} Ax+By\amp=C\amp Ax+By\amp=C\\ \substitute{0}x+By\amp=C\amp Ax+\substitute{0}y\amp=C\\ By\amp=C\amp Ax\amp=C\\ y\amp=\divideunder{C}{B}\amp x\amp=\divideunder{C}{A}\\ y\amp=k\amp x\amp=h \конец{выравнивание*}

В конце мы просто переименовали постоянные числа $\frac{C}{B}$ и $\frac{C}{A}$ в $k$ и $h$ по традиции . Важно то, что вы просматриваете $h$ и $k$ (а также $A\text{,}$ $B\text{,}$ и $C$) как константы: числа, которые имеют определенное значение и не меняются в контексте одной задачи.

Подумайте об одном из следующих уравнений: $y=k\text{.}$ Оно говорит, что значение $y$ одинаково независимо от того, где вы находитесь на линии. Если вы хотите нанести точки на эту линию, вы можете двигаться далеко влево или далеко вправо по оси $x$, но тогда вы всегда двигаетесь вверх (или вниз), чтобы сделать $y $-значение равно $k\text{.}$ Как выглядит такая строка?

Пример 3.8.6.

Давайте построим линию с уравнением $y=3\text{.}$ (Обратите внимание, что это то же самое, что $0x+1y=3\text{.}$) Чтобы нанести некоторые точки, это не Не имеет значения, какие $x$-значения мы используем. Все, что имеет значение, это то, что $y$ равно всегда $3\text{.}$

epspdfpngsvgtex

Рисунок 3.8.7. $у=3$

Такая линия горизонтальна , параллельна горизонтальной оси. Все строки с уравнением вида

\begin{уравнение*} у=к \end{уравнение*}

(или, в стандартной форме, $0x+By=C$) являются горизонтальными .

Пример 3.8.8.

Построим линию с помощью уравнения $x=5\text{.}$ Точки на линии всегда имеют $x=5\text{,}$ поэтому, если мы хотим сделать таблицу для построения точек, мы требовал , чтобы сделать все $x$-значения равными $5\text{.}$. Отсюда у нас есть полная свобода позволить $y$ принимать любое значение. Здесь мы берем некоторые случайные $y$-значения.

$х$	$у$
$5$	$-6$
$5$	$-2$
$5$	$1$
$5$	$5$

Эти точки нанесены на рисунок 3.8.9..

epspdfpngsvgtex

Рисунок 3.8.9. $х=5$

Обратите внимание, что уравнение для этой строки такое же, как $x+0y=5\text{. }$ Альтернативой для создания таблицы является выбор сначала наших $y$-значений и подстановка их в уравнение .

$у$	$х+0у=5\подразумевается х=5$	Заказанная пара
$-6$	$х+0(-6)=5\подразумевается х=5$	$(5,-6)$
$-2$	$х+0(-2)=5\подразумевается х=5$	$(5,-2)$
$1$	$х+0(1)=5\подразумевается х=5$	$(5,1)$
$5$	$х+0(5)=5\подразумевается х=5$	$(5,5)$

В каждом случае, независимо от того, какое значение $y$, мы обнаруживаем, что уравнение говорит нам, что $x=5\text{.}$

Такая линия вертикальна , параллельна вертикальной оси. Все строки с уравнением вида

\begin{уравнение*} х=ч \end{уравнение*}

(или, в стандартной форме, $Ax+0y=C$) вертикальны.

Пример 3.

8.10. Нулевой уклон.

В контрольной точке 3.4.17 мы узнали, что наклон горизонтальной линии равен $0\text{,}$, поскольку расстояние не меняется с течением времени. Таким образом, числитель в формуле наклона (3.4.3) равен $0\text{.}$. Теперь, если мы знаем наклон линии и ее точку пересечения $y$, мы можем использовать форму точки пересечения наклона (3.5 .1) написать его уравнение:

\начать{выровнять*} у\амп=мх+б\\ у\усилитель=0x+b\\ у\ампер=б \end{выравнивание*}

Это дает нам альтернативный способ думать об уравнениях горизонтальных линий. Они имеют некоторый $y$-перехват $b\text{,}$ и имеют наклон $0\text{.}$

Мы используем горизонтальные линии для моделирования сценариев, в которых значения $y$ не изменяются, например, когда Като остановился на $12$ часов (он заслужил отдых)!

КПП 3.8.11. Точки построения.

Пример 3.8.12. Наклон вертикальной линии.

Каков наклон вертикальной линии? На рис. 3.8.13 показаны три линии, проходящие через начало координат, каждая из которых круче предыдущей. На каждом графике вы можете увидеть треугольник наклона, в котором используется «пробег» в $1$ единицы.

epspdfpngsvgtex

Рисунок 3.8.13.

Если бы мы продолжали делать линию все круче и круче, пока она не стала вертикальной, треугольник наклона по-прежнему имел бы «пробег» $1\text{,}$, но «подъем» становился бы все больше и больше без верхнего предела . Наклон будет равен $m=\frac{\text{очень большой}}{1}\text{.}$ На самом деле, если линия вертикальна, нарисованный нами «подъемный» сегмент никогда не пересекает линию. . Таким образом, наклон вертикальной линии можно считать «бесконечно большим». Обычно мы говорим, что наклон вертикальной линии равен не определено . Некоторые люди говорят, что вертикальная линия не имеет наклона.

Факт 3.8.14.

Наклон вертикальной линии не определен.

КПП 3.8.16. Точки построения.

Пример 3.8.17.

Пусть $x$ представляет собой цену нового $60$-дюймового телевизора в Target в Черную пятницу (которая составляла $\$650$), а $y$ — количество часов, в течение которых вы будет смотреть что-то на этом телевизоре за всю его жизнь. Какая связь между $x$ и $y\text{?}$

Что ж, нельзя обойти стороной тот факт, что $x=650\text{.}$ Что касается $y\text{,}$ без дополнительной информации о ваших привычках просмотра, то теоретически оно может быть столь же низким как $0$ или может быть больше. Если мы нарисуем этот сценарий, мы должны изобразить уравнение $x=650$, которое, как мы теперь знаем, дает вертикальную линию, и мы получим рисунок 3.8.18.

epspdfpngsvgtex

Рисунок 3.8.18. Новый телевизор: количество часов просмотра по сравнению с ценой покупки; отрицательные $y$-значения опущены, так как они не имеют смысла в контексте

Горизонтальные линии	Вертикальные линии
Линия является горизонтальной тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение} у=к \end{уравнение} для некоторой константы $k\text{.}$	Линия вертикальна тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение} х=ч \end{уравнение} для некоторой константы $h\text{. }$
В стандартной форме (3.7.1) любая строка с уравнением \begin{уравнение} 0x+By=С \end{уравнение} горизонтальный.	В стандартной форме (3.7.1) любая строка с уравнением \begin{уравнение} Ах+0у=С \end{уравнение} вертикальный.
Если линия с уравнением $y=k$ горизонтальна, она имеет точку пересечения $y$ в точке $(0,k)$ и наклон $0\text{.} $	Если линия с уравнением $x=h$ вертикальна, она имеет точку пересечения $x$ в точке $(h,0)$ и ее наклон равен не определено . Одни говорят, что у него , а не наклон, а другие говорят, что наклон бесконечно большой .
В форме пересечения наклона (3.5.1) любая линия с уравнением \begin{уравнение} у=0х+б \end{уравнение} горизонтальный.	Невозможно записать уравнение вертикальной линии в форме пересечения наклона (3. 5.1), поскольку вертикальные линии не имеют определенного наклона.

Рисунок 3.8.19. Краткое изложение уравнений горизонтальной и вертикальной линий

Подраздел 3.8.2 Параллельные линии

Пример 3.8.20.

Два дерева были посажены в один и тот же год, и их рост с течением времени моделируется двумя линиями на рисунке 3.8.21. Используйте линейные уравнения для моделирования роста каждого дерева и интерпретируйте их значения в этом контексте.

Мы видим, что уравнение Дерева 1 имеет вид $y=\frac{2}{3}x+2\text{,}$, а уравнение Дерева 2 имеет вид $y=\frac{2}{3}x+ 5\text{.}$ Дерево 1 было $2$ футов высотой, когда оно было посажено, а Дерево 2 было $5$ футов высотой, когда оно было посажено. Оба дерева растут с одинаковой скоростью, $\frac{2}{3}$ футов в год или $2$ футов каждые $3$ лет.

epspdfpngsvgtex

Рисунок 3.8.21. Диаграмма роста двух деревьев

Сейчас важно отметить, что эти две линии параллельны. Почему? Для линий с положительным наклоном чем больше наклон линии, тем круче наклон линии. В результате, если две линии имеют одинаковый наклон, они наклонены под одним и тем же углом, следовательно, они параллельны.

Факт 3.8.22.

Любые две вертикальные линии параллельны друг другу. Две невертикальные прямые параллельны тогда и только тогда, когда они имеют одинаковый наклон.

КПП 3.8.23.

КПП 3.8.24.

Подраздел 3.8.3 Перпендикулярные линии

Наклоны двух перпендикулярных линий также имеют особое отношение.

На рис. 3.8.25 показано объяснение этой взаимосвязи.

epspdfpngsvgtex

(a) Две общие перпендикулярные линии, одна из которых имеет наклон $m\text{.}$

epspdfpngsvgtex

(b) Так как один наклон равен $m\text{,}$, мы можем нарисовать треугольник наклона со значениями «бег» $1$ и «подъем» $m\text{.}$

epspdfpngsvgtex

(c) -конгруэнтный треугольник наклона может быть нарисован для перпендикулярной линии. Его ноги имеют одинаковую длину, но в разных положениях, и одна из них отрицательная.

Рисунок 3.8.25. Соотношение между наклонами перпендикулярных линий

. Вторая линия на рисунке 3.8.25 имеет наклон

\begin{уравнение*} \frac{\Delta y}{\Delta x}=\frac{-1}{m}=-\frac{1}{m}\text{.} \end{уравнение*}

Факт 3.8.26.

Вертикальная линия и горизонтальная линия перпендикулярны. Для двух линий, которые не являются ни вертикальными, ни горизонтальными, они перпендикулярны тогда и только тогда, когда наклон одной является отрицательной обратной величиной наклона другой. То есть, если у одного есть наклон $m\text{,}$, у другого есть наклон $-\frac{1}{m}\text{.}$

Другой способ сказать это так: произведение наклонов двух перпендикулярных линий равно $-1$ (предполагая, что обе линии изначально имеют наклон). То есть, если есть две перпендикулярные линии, и мы допустим, что $m_1$ и $m_2$ представляют их наклоны, тогда $m_1\cdot m_2=-1\text{.}$

Не уверены? Вот три пары перпендикулярных линий, по которым мы можем видеть, сохраняется ли шаблон.

epspdfpngsvgtex

Рисунок 3.8.27. Графики $y=2x-2$ и $y=-\frac{1}{2}x+2\text{.}$ Обратите внимание на соотношение между их наклонами: $2=-\frac{1 }{-\sfrac{1}{2}}$

epspdfpngsvgtex

Рисунок 3.8.28. Графики $y=-3x+4$ и $y=\frac{1}{3}x-3\text{.}$ Обратите внимание на соотношение между их наклонами: $-3=-\frac{ 1}{\sfrac{1}{3}}$

epspdfpngsvgtex

Рисунок 3.8.29. Графики $y=x$ и $y=-x\text{.}$ Обратите внимание на соотношение между их наклонами: $1=-\frac{1}{-1}$

Пример 3.8.30.

Линия $A$ проходит через $(-2,10)$ и $(3,-10)\text{.}$ Линия $B$ проходит через $(-4,- 4)$ и $(8,-1)\text{.}$ Определите, являются ли эти две прямые параллельными, перпендикулярными или ни тем, ни другим.

Объяснение

Мы будем использовать формулу наклона, чтобы найти наклоны обеих линий:

\begin{align*} \text{Линия }A\text{наклон}\amp=\frac{y_2-y_1}{x_2-x_1}\amp\text{Линия }B\text{наклон}\amp=\frac{y_2 -y_1}{x_2-x_1}\\ \amp=\frac{-10-10}{3-(-2)}\amp\amp=\frac{-1-(-4)}{8-(-4)}\\ \amp=\frac{-20}{5}\amp\amp=\frac{3}{12}\\ \amp=-4\amp\amp=\frac{1}{4} \end{align*}

Их наклоны не одинаковы, поэтому эти две линии не параллельны.

Произведение их наклонов равно $(-4)\cdot\frac{1}{4}=-1\text{,}$, что означает, что две линии перпендикулярны.

КПП 3.8.31.

Вопросы для чтения 3.8.4 Вопросы для чтения

1.

Объясните разницу между линией без наклона и линией с наклоном $0\text{.}$

2.

Если составить таблицу значений $x$ и $y$ для горизонтальной или вертикальной линии, что произойдет в одном из двух столбцов?

3.

Если вам известны две точки на одной прямой и две точки на другой прямой, что вы можете сделать, чтобы определить, перпендикулярны ли эти две прямые?

Упражнения 3.8.5 Упражнения

Обзор и прогрев

1.

Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).

$\displaystyle{ \frac{7}{0} = }$
$\displaystyle{ \frac{0}{7} = }$

2.

Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).

$\displaystyle{ \frac{0}{8} = }$
$\displaystyle{ \frac{8}{0} = }$

3.

Прямая проходит через точки $(5,8)$ и $(-3,8)\text{.}$ Найдите наклон этой линии.

4.

Прямая проходит через точки $(3,10)$ и $(-1,10)\text{.}$ Найдите наклон этой линии.

5.

Прямая проходит через точки $(-8,-5)$ и $(-8,3)\text{.}$ Найдите наклон этой линии.

6.

Прямая проходит через точки $(-6,-1)$ и $(-6,5)\text{.}$ Найдите наклон этой линии.

7.

Рассмотрим уравнение:

\begin{уравнение*} у=1 \end{уравнение*}

Какие из следующих упорядоченных пар являются решениями данного уравнения? Может быть более одного правильного ответа.

$(4,1)$
$(-4,1)$
$(0,7)$
$(1,4)$

8.

Рассмотрим уравнение:

\begin{уравнение*} у=1 \end{уравнение*}

$(-6,1)$
$(5,1)$
$(0,9)$
$(1,2)$

9.

Рассмотрим уравнение:

\begin{уравнение*} х+1=0 \end{уравнение*}

$(-1,0)$
$(-1,3)$
$(0,-6)$
$(1,-1)$

10.

Рассмотрим уравнение:

\begin{уравнение*} х+1=0 \end{уравнение*}

$(1,-1)$
$(-1,0)$
$(0,-8)$
$(-1,4)$

Столы для горизонтальных и вертикальных линий

11.

Заполните эту таблицу для уравнения $y=8\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-3$	$8$	$\влево(-3,8\вправо)$
$-2$
$-1$
$0$
$1$
$2$

12.

Заполните эту таблицу для уравнения $y=9\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-3$	$9$	$\влево(-3,9\вправо)$
$-2$
$-1$
$0$
$1$
$2$

13.

Заполните эту таблицу для уравнения $x=-1\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-1$	$-3$	$\влево(-1,-3\вправо)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

14.

Заполните эту таблицу для уравнения $x=-9\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-9$	$-3$	$\влево(-9,-3\вправо)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

Линейные уравнения

15.

Показан линейный график. Напишите уравнение прямой.

epspdfpngsvgtex

16.

Показан линейный график. Напишите уравнение прямой.

epspdfpngsvgtex

17.

Показан линейный график. Напишите уравнение прямой.

epspdfpngsvgtex

18.

Показан линейный график. Напишите уравнение прямой.

epspdfpngsvgtex

19.

Прямая проходит через точки $(-2,3)$ и $(-3,3)\text{.}$ Найдите уравнение для этой прямой.

Уравнение для этой линии .

20.

Прямая проходит через точки $(5,6)$ и $(2,6)\text{.}$ Найдите уравнение для этой прямой.

Уравнение для этой линии .

21.

Прямая проходит через точки $(8,1)$ и $(8,-5)\text{.}$ Найдите уравнение для этой прямой.

Уравнение для этой линии .

22.

Прямая проходит через точки $(10,-3)$ и $(10,0)\text{.}$ Найдите уравнение для этой прямой.

Уравнение для этой линии .

Перехваты

23.

Найдите точку пересечения $y$ и точку пересечения $x$ прямой, заданной уравнением. Если определенного перехвата не существует, введите нет во все поля для ответов в этой строке.

\begin{уравнение*} х = -8 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

24.

\begin{уравнение*} х = -6 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$у$-перехват
$х$-перехват

25.

\begin{уравнение*} у = -4 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$у$-перехват
$х$-перехват

26.

\begin{уравнение*} у = -1 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

Графики горизонтальных и вертикальных линий

27.

Нарисуйте линию $y=1\text{.}$

28.

Нарисуйте линию $y+5=0\text{.}$

29.

Нарисуйте линию $x=2\text{.}$

30.

Нарисуйте линию $x-3=0\text{.}$

Параллельно или перпендикулярно?

31.

Линия $m$ проходит через точки $(1,3)$ и $(-3,-9)\text{.}$

Линия $n$ проходит через точки $(5,20)$ и $(4,17)\text{.}$

Эти две строки

32.

Линия $m$ проходит через точки $(-21,28)$ и $(-7,16)\text{.}$

Линия $n$ проходит через точки $(-35,33)$ и $(7,-3)\text{.}$

Эти две строки равны

33.

Линия $m$ проходит через точки $(-5,8)$ и $(5,6)\text{.}$

Линия $n$ проходит через точки $(-4,-16)$ и $(2,14)\text{.}$

Эти две строки

34.

Линия $m$ проходит через точки $(-5,15)$ и $(5,-1)\text{.}$

Строка $n$ проходит через точки $(-16,0)$ и $(-24,-5)\text{. }$

Эти две строки

35.

Линия $m$ проходит через точки $(-3,-5)$ и $(-4,-4)\text{.}$

Линия $n$ проходит через точки $(-2,-9)$ и $(1,3)\text{.}$

Эти две строки

36.

Линия $m$ проходит через точки $(6,-8)$ и $(4,-8)\text{.}$

Линия $n$ проходит через точки $(3,7)$ и $(10,7)\text{.}$

Эти две строки

37.

Линия $m$ проходит через точки $(-6,-2)$ и $(-6,-9)\text{.}$

Линия $n$ проходит через точки $(1,3)$ и $(1,-1)\text{.}$

Эти две строки

38.

Линия $m$ проходит через точки $(-4,-9)$ и $(-4,0)\text{.}$

Линия $n$ проходит через точки $(3,10)$ и $(3,1)\text{.}$

Эти две строки равны

Уравнения параллельных и перпендикулярных линий

39.

Прямая проходит через точку $(9,5)\text{,}$ и параллельна прямой $y=-2\text{.}$ Найдите уравнение для этой прямой.

40.

Прямая проходит через точку $(-3,-2)\text{,}$ и параллельна прямой $y=1\text{.}$ Найдите уравнение для этой прямой.

41.

Прямая проходит через точку $(-10,5)\text{,}$ и параллельна прямой $x=3\text{.}$ Найдите уравнение для этой прямой.

42.

Прямая проходит через точку $(4,-7)\text{,}$ и параллельна прямой $x=5\text{.}$ Найдите уравнение для этой прямой.

43.

Строка $k$ имеет уравнение $y={4x-2}\text{.}$

Прямая $\ell$ параллельна прямой $k\text{,}$, но проходит через точку $(4,{18})\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

44.

Строка $k$ имеет уравнение $y={5x+5}\text{.}$

Прямая $\ell$ параллельна прямой $k\text{,}$, но проходит через точку $(1,{-5})\text{. }$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

45.

Строка $k$ имеет уравнение $y={-{\frac{1}{7}}x-3}\text{.}$

Прямая $\ell$ параллельна прямой $k\text{,}$, но проходит через точку $(-2,{-{\frac{5}{7}}})\text{ .}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

46.

Линия $k$ имеет уравнение $y={-{\frac{2}{9}}х+10}\текст{.}$

Прямая $\ell$ параллельна прямой $k\text{,}$, но проходит через точку $(3,{-{\frac{11}{3}}})\text{. }$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

47.

Строка $k$ имеет уравнение $y={-x+9}\text{.}$

Прямая $\ell$ перпендикулярна прямой $k\text{,}$ и проходит через точку $(-1,{-4})\text{.}$

Найдите уравнение для линии $\ell\text{.}$

48.

Строка $k$ имеет уравнение $y={4x+2}\text{.}$

Прямая $\ell$ перпендикулярна прямой $k$ и проходит через точку $(2,{{\frac{9}{2}}})\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

49.

Уравнение линии $k$ равно $y={-{\frac{6}{5}}x-3}\text{.}$

Прямая $\ell$ перпендикулярна прямой $k$ и проходит через точку $(2,{{\frac{14}{3}}})\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

50.

Строка $k$ имеет уравнение ${x-9y}=-45\text{.}$

Прямая $\ell$ перпендикулярна прямой $k$ и проходит через точку $(1,{-8})\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Уравнение для $\ell$ в форме точка-наклон: .

Уравнение для $\ell$ в форме пересечения наклона: .

Вызов

51.

Докажите, что треугольник с вершинами в точках $(1, 1)\text{,}$ $(-4, 4)\text{,}$ и $(-3, 0)$ является прямоугольным треугольником.

Изучаем параллельные линии, перпендикулярные линии, горизонтальные и вертикальные линии

Параллельные линии и перпендикулярные линии.

Две невертикальные прямые параллельны тогда и только тогда, когда они имеют одинаковый наклон. Этот факт довольно интуитивен, поскольку две линии, которые не поднимаются и не опускаются с одинаковой скоростью, неизбежно пересекутся (как и две линии, одна из которых поднимается, а другая опускается).

Менее интуитивный, но столь же верный факт заключается в том, что две линии, ни одна из которых не является вертикальной, перпендикулярны тогда и только тогда, когда они имеют противоположные взаимные наклоны. Например, если линия имеет наклон $-\frac{9}{11}\text{,}$, чем любая линия, перпендикулярная этой линии, имеет наклон $\frac{11}{9}$

Пример 7.6.1.

Определите уравнение пересечения наклона линии, которая проходит через точку $(9,-2)$ и параллельна линии с уравнением $x-3y=14\text{.}$

Решение

Начнем с определения наклона линии $x-3y=14\text{.}$ Мы можем сделать это, записав уравнение в форме пересечения наклона, что по существу влечет за собой выделение $y\text {.}$

\begin{выравнивание*} х-3у\ампер=14\\ x-3y\вычесть вправо{х}\amp=14\вычесть вправо{х}\\ -3y\amp=-x+14\\ \multiplyleft{-\frac{1}{3}}-3y\amp=\multiplyleft{-\frac{1}{3}}(-x+14)\\ y=\frac{1}{3}x-\frac{14}{3} \end{align*}

Из уравнения $y=\frac{1}{3}x-\frac{14}{3}$ мы можем определить, что наклон линии $x-3y= 14 $ равно $\frac{1}{3}\text{. }$ Поскольку прямая, уравнение которой мы ищем, параллельна $x-3y=14\text{,}$ и параллельные прямые имеют равные наклон, наклон искомой линии также равен $\frac{1}{3}\text{.}$

Линия, которую нам нужно определить, имеет наклон $\frac{1}{3}$ и проходит через точку $(9,-2)\text{.}$ Используя эту информацию в точечно-наклонной формы линейного уравнения и упрощая результат, уравнение наклона-пересечения для линии определяется следующим образом.

\начать{собирать*} у-у_1=м(х-х_1)\\ у-(-2)=\фракция{1}{3}(х-9)\\ у+2=\фракция{1}{3}х-3\\ y+2\subtractright{2}=\frac{1}{3}x-3\subtractright{2}\\ у=\фракция{1}{3}-5 \конец{собрать*}

Пример 7.6.2.

Давайте составим уравнение пересечения наклона линии, проходящей через точку $(-8,16)$, которая перпендикулярна линии, проходящей через точки, показанные на рисунке 7.6.3.

$х$	$у$
$-4$	$7$
$10$	$-5$

Рисунок 7.

6.3. Точки на линии

Решение

Начнем с определения наклона линии, проходящей через точки, показанные на рисунке 7.6.3. Пусть $(x_1,y_1)$ будет упорядоченной парой $(-4,7)$ и $(x_2,y_2)$ будет упорядоченным $(10,-5)\text{,} $ мы вычисляем наклон следующим образом.

\begin{выравнивание*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-5-7}{10-(-4)}\\ \amp=\frac{-12}{14}\\ \amp=-\frac{6}{7} \end{align*}

Поскольку искомая линия перпендикулярна линии с наклоном $-\frac{6}{7}\text{,}$, а перпендикулярные линии имеют противоположные обратные наклоны, линия мы ищем, имеет наклон $\frac{7}{6}\text{.}$

Используя наклон $\frac{7}{6}$ и упорядоченную пару $(-8 ,16)\text{,}$ определяем уравнение пересечения наклона искомой прямой следующим образом.

\начать{собирать*} у-у_1=м(х-х_1)\\ y-16=\frac{7}{6}(x-(-8))\\ у-16 = \ гидроразрыва {7} {6} (х + 8) \\ y-16=\frac{7}{6}x+\frac{28}{3}\\ y-16 \ addright {16} = \ frac {7} {6} x + \ frac {28} {3} \ addright {\ frac {48} {3}} \\ y=\frac{7}{6}x+\frac{76}{3} \end{gather*}

Горизонтальные линии.

Уравнение горизонтальной линии можно определить так же, как и любую другую невертикальную линию, хотя после того, как это сделано, обобщение может значительно упростить процесс.

Рассмотрим горизонтальную линию, показанную на рисунке 7.6.4. Пусть $(x_1,y_1)$ будет упорядоченной парой $(-4,-3)$ и $(x_2,y_2)$ будет упорядоченной парой $(2,-3)\text{ .}$ Мы вычисляем наклон ниже.

Рисунок 7.6.4. Горизонтальная линия

\начать{выровнять*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-3-(-3)}{2-(-4)}\\ \amp=\frac{0}{6}\\ \усилитель=0 \конец{выравнивание*}

По наблюдениям, $y$-пересечение линии равно $(0,-3)\text{.}$ Это в сочетании с наклоном $0$ дает нам следующее.

\начать{выровнять*} у\амп=мх+б\\ y\amp=0 \cdot x+(-3)\\ у\ампер=-3 \конец{выравнивание*}

Теперь, когда у нас есть уравнение $y=-3\text{,}$, подходящим ответом может быть «d’oh!» По наблюдениям, определяющее свойство точек на прямой состоит в том, что все $y$-координаты равны $-3$

В общем, все горизонтальные линии имеют наклон $0\text{. }$ Кроме того, горизонтальная линия имеет уравнение формы $y=k$, где $k$ — это $y $-координата, общая для каждой точки прямой.

Вертикальные линии.

Рассмотрим вертикальную линию, показанную на рисунке 7.6.5. Когда мы пытаемся вычислить наклон линии, все выходит из-под контроля. Например:

\begin{выравнивание*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{5-(-3)}{2-2}\\ \amp=\frac{8}{0} \end{align*}

Рисунок 7.6.5. Вертикальная линия

К последнему выражению мы присоединяем фразу —у-у-у! Деление на $0$ никогда не бывает хорошим. Деление на ноль всегда является результатом применения формулы наклона к вертикальной линии, и по этой причине мы говорим, что вертикальная линия не имеет наклона или что наклон не определен.

На рис. 7.6.5 видно, что каждая точка на прямой имеет $x$-координату $2\text{,}$, поэтому уравнение прямой должно быть $x=2\text {.}$ В общем, вертикальные линии имеют уравнения вида $x=h\text{,}$, где $h$ — $x$-координата каждой точки на линии

Итак, в отличие от определения уравнений невертикальных, негоризонтальных линий, определение уравнения горизонтальной или вертикальной линии — это просто вопрос записи уравнения.

Например, если вас попросят определить уравнения для горизонтальных и вертикальных линий, проходящих через точку $(-3,7)\text{,}$, соответствующий ответ будет следующим.

Горизонтальная линия имеет уравнение $y=7$, а вертикальная линия имеет уравнение $x=-3\text{.}$

Если в данный момент вы не можете вспомнить, какая форма уравнения горизонтальна, а какая вертикальна, просто нарисуйте линию и спросите себя, «какая координата всегда одна и та же, $x$ или $y\text{ ?}$»

Упражнения Упражнения

1.

Укажите уравнения вертикальной и горизонтальной линий, проходящих через точку $(-7,25)\text{.}$

Решение

Уравнение вертикальной линии $y=25$, а уравнение горизонтальной линии $x=-7$

2.

Каковы наклоны линий, параллельных прямой с уравнением $-6x+8y=12\text{?}$ Каковы наклоны линий, перпендикулярных этим линиям?

Решение

Начнем с преобразования уравнения $-6x+8y=12$ в форме пересечения наклона.

\begin{выравнивание*} -6x+8y\amp=12\\ -6x+8y\addright{6x}\amp=12\addright{6x}\\ 8у\ампер=6х+12\\ \multipleleft{\frac{1}{8}}(8y) \amp=\multipleleft{\frac{1}{8}}(6x+12)\\ y\amp=\frac{3}{4}x+\frac{3}{2} \end{align*}

Из последнего уравнения видно, что наклон линии $-6x+8y=12$ равен $\frac{3}{4}\text{.}$ Итак все линии, параллельные $-6x+8y=12$, имеют наклоны $\frac{3}{4}$, а линии, перпендикулярные этим линиям, имеют наклоны $-\frac{4}{3}\ текст{.}$

3.

Определите уравнения линий, проходящих через точку $(3,5)$ и соответственно параллельных и перпендикулярных линии, изображенной на рисунке 7.6.6. Сформулируйте каждое уравнение в форме пересечения наклона.

Рисунок 7.6.6. Определить уравнение…

Решение

Линия, изображенная на рисунке 7.6.6, имеет наклон $-\frac{1}{2}$, поэтому линии, параллельные этой линии, имеют наклон $-\frac{1}{2}\ ) и прямые, перпендикулярные ему, имеют наклон \(2\text{. }$

Используя наклон $-\frac{1}{2}$ и упорядоченную пару $(3,5)$ в уравнении $y-y_1=m(x-x_1)$, мы вывести уравнение описанной параллельной прямой следующим образом.

\begin{выравнивание*} y-5\amp=-\frac{1}{2}(x-3)\\ y-5\amp=-\frac{1}{2}x+\frac{3}{2}\\ y-5 \ addright {5} \ amp = — \ frac {1} {2} x + \ frac {3} {2} \ addright {\ frac {10} {2}} \\ y\amp=-\frac{1}{2}x+\frac{13}{2} \end{align*}

Используя наклон $2$ и упорядоченную пару $(3,5)$ в уравнении $y-y_1=m(x-x_1)$, мы получаем уравнение описанной перпендикулярной прямой выглядит следующим образом.

\begin{выравнивание*} у-5\ампер=2(х-3)\\ у-5\ампер=2x-6\\ y-5\addright{5}\amp=2x-6\addright{5}\\ у\ампер=2x-1 \end{align*}

Две новые строки показаны на рисунке 7.6.7 вместе с данной строкой. Они действительно параллельны или перпендикулярны данной прямой.

Рисунок 7.6.7. Визуальная проверка

4.

Определите уравнение прямой, проходящей через точку $(9,-2)$ и перпендикулярной прямой с уравнением $y=14\text{. }$

Решение

Линия $y=14$ горизонтальна, поэтому любая прямая, перпендикулярная ей, вертикальна. Следовательно, прямая, проходящая через точку $(9,-2)$ и перпендикулярна прямой $y=14$ имеет уравнение $x=9\text{.}$

5.

Определите уравнение прямой, проходящей через точку $(-3,14)$ и перпендикулярной прямой с уравнением $12x-4y=18\text{.}$ Уравнение состояния в наклоне-пересечении форма.

Решение

Начнем с того, что запишем уравнение $12x-4y=18$ в форме пересечения наклона.

\begin{выравнивание*} 12x-4y\amp=18\\ 12x-4y\subtractright{12x}\amp=18\subtractright{12x}\\ -4у\ампер=-12х+18\\ \multiplyleft{-\frac{1}{4}}(-4y)\amp=\multiplyleft{-\frac{1}{4}}(-12x+18)\\ y\amp=3x-\frac{9{2} \end{align*}

Из последнего уравнения видно, что наклон линии $12x-4y=18$ равен $3\text{.}$ Таким образом, любая линия, перпендикулярная $12x- 4y=18$ имеет наклон $-\frac{1}{3}\text{. }$ Используя новый наклон вместе с упорядоченной парой $(-3,14)$ в точке- уравнение наклона мы получаем уравнение запрошенной линии таким образом:

\begin{align*} у-у_1\амп=м(х-х_1)\\ y-14\amp=-\frac{1}{3}(x-(-3))\\ y-14\amp=-\frac{1}{3}x-1\\ y-14\addright{14}\amp=-\frac{1}{3}x-1\addright{14}\\ y\amp=-\frac{1}{3}x+13 \end{выравнивание*}

7.4: Уравнения вертикальных и горизонтальных линий

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 45198

Виктория Домингес, Кристиан Мартинес и Санаа Сайкали
Citrus College через Инициативу открытых образовательных ресурсов ASCCC

Определение: вертикальная линия

Уравнение вертикальной линии имеет вид $x = c$, где $c$ — любое действительное число. Вертикальная линия всегда будет пересекать ось $x$ в точке $(c, 0)$. Наклон вертикальной линии равен undefined .

Пример 7.4.1

Найдите наклон линии $x = 4$ и нарисуйте линию.

Раствор

$x = 4$ представляет собой график вертикальной линии, как показано на рисунке ниже.

Чтобы найти наклон линии $x = 4$, выберите любые две различные точки на линии. Пусть это точки $(4, −1)$ и $(4, 3)$. Используя формулу наклона линии,

$\begin{array} && m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Формула наклона линии} \\ &= \dfrac{3 − (−1)}{4 − 4} &\text{Подстановка значений} \\ &= \dfrac{4}{0} &\text{Упрощение} \end{массив}$

Теперь, если $4$ разделить на $0$, это эквивалентно заданию вопроса: «Какое число, умноженное на ноль, дает $4$?» ответ в том, что такого номера нет. Деление на ноль не определено, а наклон вертикальной линии $x = 4$ равен undefined .

Определение: Горизонтальная линия

Уравнение горизонтальной линии имеет форму $y = k$, где $k$ — любое действительное число. Горизонтальная линия всегда будет пересекать ось $y$ в точке $(0, k)$. Наклон горизонтальной линии равен Ноль .

Пример 7.4.2

Найдите наклон прямой, проходящей через точки $(−3, −2)$ и $(4, −2)$. Нанесите точки и начертите линию, проходящую через них.

Раствор

Используйте формулу наклона линии. Таким образом,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Формула наклона линии} \\ &= \dfrac{(−2) − (−2)} {4 − (−3)} &\text{Подстановка значений} \\ &= \dfrac{0}{7} &\text{Упрощение} \\ &= 0 &\text{\(0$ разделить на любое ненулевое число равно нулю} \end{массив}\)

Таким образом, линия, проходящая через две заданные точки, является горизонтальной линией с нулевым наклоном, как показано на рисунке ниже.

Пример 7.4.3

Нарисуйте прямую $y − 3 = 0$ и найдите ее наклон.

Раствор

Строка $y − 3 = 0$ может быть записана как $y = 3$ (добавьте $3$ к обеим частям уравнения). Линия $y = 3$ является горизонтальной линией, как показано на рисунке ниже.

Теперь, чтобы найти наклон, выберите любые две различные точки на линии $y = 3$. Рассмотрим точки $(0, 3)$ и $(3, 3)$. Таким образом,

$\begin{array} && m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Формула наклона линии} \\ &= \dfrac{3-3}{3-0} & \text{Подстановка значений} \\ &= \dfrac{0}{2} &\text{Упрощение} \\ &= 0 &\text{\(0$ деленное на любое ненулевое число равно нулю} \end {массив}\)

Следовательно, наклон данной прямой равен $m = 0.$

Упражнение 7.4.1

Найдите наклон каждой линии.

$х = -\dfrac{1}{2}$
$у — 1 = 0$
$х + 7 = 10$
$у + 2 = -9$
Найдите наклон прямой, проходящей через точки $(−4, 1)$ и $(2, 1)$. Нанесите точки и начертите линию, проходящую через них.
Найдите наклон прямой, проходящей через точки $(−3, 5)$ и $(−3, −7)$. Нанесите точки и начертите линию, проходящую через них.

Эта страница под названием 7.4: Уравнения вертикальных и горизонтальных линий распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Викторией Домингес, Кристианом Мартинесом и Санаа Сайкали (ASCCC Open Educational Resources Initiative ).

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Виктория Домингес, Кристиан Мартинес и Сана Сайкали
Лицензия
СС BY-SA
Версия лицензии
4,0
Программа ООР или издатель
Программа ASCCC OERI
Показать страницу Содержание
нет
Теги
1. горизонтальная линия
2. не определено
3. вертикальная линия

ORCCA Горизонтальные, вертикальные, параллельные и перпендикулярные линии

Горизонтальные и вертикальные линии имеют некоторые особенности, заслуживающие нашего внимания. Кроме того, если пара прямых параллельна или перпендикулярна друг другу, мы можем сказать о них кое-что интересное. В этом разделе рассматриваются эти геометрические особенности, которые могут иметь линии.

Рисунок 4.8.1. Горизонтальная линия Рисунок 4.8.2. Вертикальная линия Рисунок 4.8.3. Параллельные линии Рисунок 4.8.4. Перпендикулярные линии

Подраздел 4.8.1 Горизонтальные линии и вертикальные линии

В разделе 4.7 мы узнали, что все строки можно записать в стандартной форме. Когда $A$ или $B$ равно $0\text{,}$, мы получаем горизонтальную или вертикальную линию, как мы скоро увидим. Давайте возьмем линейное уравнение стандартной формы, пусть $A=0$ и $B=0$ по одному, и упростим каждое уравнение.

\начать{выравнивать*} Ax+By\amp=C\amp Ax+By\amp=C\\ \substitute{0}x+By\amp=C\amp Ax+\substitute{0}y\amp=C\\ By\amp=C\amp Ax\amp=C\\ y\amp=\divideunder{C}{B}\amp x\amp=\divideunder{C}{A}\\ y\amp=k\amp x\amp=h \конец{выравнивание*}

Подумайте хотя бы об одном из этих последних уравнений: $y=k\text{.}$ Оно говорит, что значение $y$ одинаково независимо от того, где вы находитесь на линии. Если вы хотите нанести точки на эту линию, вы можете двигаться далеко влево или далеко вправо по оси $x$, но тогда вы всегда двигаетесь вверх (или вниз), чтобы сделать $y $-значение равно $k\text{.}$ Как выглядит такая строка?

Пример 4.8.5.

Давайте построим линию с уравнением $y=3\text{.}$ (Обратите внимание, что это то же самое, что и $0x+1y=3\text{.}$)

Для построения точек не имеет значения, какие $x$-значения мы используем. Все, что имеет значение, это то, что $y$ всегда $3\text{.}$

Такая линия горизонтальна , параллельна горизонтальной оси. Все строки с уравнением вида

\begin{equation*} у=к \end{equation*}

(или, в стандартной форме, $0x+By=C$) по горизонтали .

Рисунок 4.8.6. $у=3$

Пример 4.8.7.

Давайте построим линию с уравнением $x=5\text{.}$ (Обратите внимание, что это то же самое, что $1x+0y=5\text{.}$)

Линия имеет $x=5\text{,}$, поэтому для построения точек нам требуется , чтобы перейти к $x=5\text{.}$ Оттуда у нас есть полная свобода двигаться так далеко, как нам нравится вверх или вниз.

Такая линия вертикальна , параллельна вертикальной оси. Все строки с уравнением вида

\begin{equation*} х=ч \end{equation*}

(или, в стандартной форме, $Ax+0y=C$) вертикальны.

Рисунок 4.8.8. $х=5$

Пример 4.8.9. Нулевой уклон.

В контрольной точке 4.4.16 мы узнали, что наклон горизонтальной линии равен $0\text{,}$ . Таким образом, числитель в формуле наклона равен $0\text{.}$. Теперь, если мы знаем наклон линии и ее точку пересечения $y$, мы можем использовать форму точки пересечения для записи уравнения:

\начать{выровнять*} у\амп=мх+б\\ у\усилитель=0x+b\\ у\ампер=б \конец{выравнивание*}

Это дает нам альтернативный способ думать об уравнениях горизонтальных линий. Они имеют некоторую $y$-пересечение $(0,b)$ и наклон $0\text{.}$

КПП 4.8.10. Точки построения.

Пример 4.8.11. Неопределенный наклон.

Каков наклон вертикальной линии? На рис. 4.8.12 показаны три линии, проходящие через начало координат, каждая из которых круче предыдущей. На каждом графике вы можете видеть треугольник наклона, который каждый раз использует «подъем» $4$.

Рисунок 4.8.12.

Если бы мы продолжали делать линию все круче и круче, пока она не стала вертикальной, треугольник наклона по-прежнему имел бы «подъем» на $4\text{,}$, но «пробег» становился бы все меньше и меньше, приближаясь к \ (0\text{.}\) И тогда наклон будет $m=\frac{4}{\text{очень маленький}}=\text{очень большой}\text{.}$ Таким образом, наклон вертикальную линию можно рассматривать как «бесконечно большую».

Если мы на самом деле попытаемся вычислить уклон, используя треугольник наклона, когда пробег равен $0\text{,}$, мы получим $\frac{4}{0}\text{,}$, который не определен . Поэтому мы также говорим, что наклон вертикальной линии равен не определено . Некоторые люди говорят, что вертикальная линия не имеет наклона.

КПП 4.8.14. Точки построения.

Пример 4.8.15.

Что ж, нельзя обойти стороной тот факт, что $x=650\text{.}$ Что касается $y\text{,}$ без дополнительной информации о ваших привычках просмотра, то теоретически оно может быть столь же низким как $0$ или может быть больше. Если мы нарисуем этот сценарий, мы должны изобразить уравнение $x=650\text{,}$, которое, как мы теперь знаем, дает вертикальную линию, и мы получим рисунок 4. 8.16.

Рисунок 4.8.16. Новый телевизор: количество часов просмотра по сравнению с ценой покупки; отрицательные $y$-значения опущены, поскольку они не имеют смысла в контексте

Краткое изложение уравнений горизонтальной и вертикальной линий.

Горизонтальные линии	Вертикальные линии
Линия является горизонтальной тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение} у=к \end{уравнение} для некоторой константы $k\text{.}$	Строка вертикальный тогда и только тогда, когда его уравнение может быть записано \begin{уравнение} х=ч \end{уравнение} для некоторой константы $h\text{.}$
В стандартной форме любая строка с уравнением \begin{уравнение} 0x+By=С \end{уравнение} горизонтальный.	В стандартной форме любая строка с уравнением \begin{уравнение} Ах+0у=С \end{уравнение} вертикальный.
Если линия с уравнением $y=k$ горизонтальна, она имеет точку пересечения $y$ в точке $(0,k)$ и наклон $0\text{.} $	Если линия с уравнением $x=h$ вертикальна, она имеет точку пересечения $x$ в точке $(h,0)$ и ее наклон равен undefined . Одни говорят, что у него , а не наклон, а другие говорят, что наклон бесконечно большой .
В форме пересечения наклона любая линия с уравнением \begin{уравнение} у=0х+б \end{уравнение} горизонтальный.	Невозможно записать уравнение вертикальной линии в форме наклон-отрезок, потому что вертикальные линии не имеют определенного наклона.

Подраздел 4.8.2 Параллельные линии

Пример 4.8.17.

Два дерева были посажены в один и тот же год, и их рост с течением времени моделируется двумя линиями на рисунке 4.8.18. Используйте линейные уравнения для моделирования роста каждого дерева и интерпретируйте их значения в этом контексте.

Рисунок 4.8.18. Диаграмма роста двух деревьев

Мы видим, что уравнение Дерева 1 имеет вид $y=\frac{2}{3}x+2\text{,}$, а уравнение Дерева 2 имеет вид $y=\frac{2}{3}x+5 \text{.}$ Дерево 1 было $2$ футов высотой, когда оно было посажено, а Дерево 2 было $5$ футов высотой, когда оно было посажено. Оба дерева растут с одинаковой скоростью, $\frac{2}{3}$ футов в год или $2$ футов каждые $3$ лет.

Факт 4.8.19.

КПП 4.8.20.

КПП 4.8.21.

Подраздел 4.8.3 Перпендикулярные линии

Наклоны двух перпендикулярных линий также имеют особое отношение.

На рис. 4.8.22 показано объяснение этой связи.

(a) Две общие перпендикулярные линии, одна из которых имеет наклон $m\text{.}$(b) Поскольку один наклон равен $m\text{,}$, мы можем нарисовать треугольник наклона с помощью «run» $1$ и «подниматься» $m\text{.}$(c) A конгруэнтный треугольник наклона можно нарисовать для перпендикулярной линии. Его ноги имеют одинаковую длину, но в разных положениях, и одна из них отрицательная. Рисунок 4.8.22. Соотношение между наклонами перпендикулярных линий

. Вторая линия на рисунке 4.8.22 имеет наклон

\begin{уравнение*} \frac{\Delta y}{\Delta x}=\frac{-1}{m}=-\frac{1}{m}\text{. } \end{уравнение*}

Факт 4.8.23.

Вертикальная линия и горизонтальная линия перпендикулярны. Для линий, которые не являются ни вертикальными, ни горизонтальными, они перпендикулярны тогда и только тогда, когда наклон одной является отрицательной обратной величиной наклона другой. То есть, если у одного есть наклон $m\text{,}$, у другого есть наклон $-\frac{1}{m}\text{.}$

Другой способ сказать это так: произведение наклонов двух перпендикулярных линий равно $-1$ (предполагая, что обе линии изначально имеют наклон).

Не убежден? Вот три пары перпендикулярных линий, по которым мы можем видеть, сохраняется ли шаблон.

Рисунок 4.8.24. Графики $y=2x-2$ и $y=-\frac{1}{2}x+2\text{.}$ Обратите внимание на соотношение между их наклонами: $2=-\frac{1 }{-\sfrac{1}{2}}$Рисунок 4.8.25. Графики $y=-3x+4$ и $y=\frac{1}{3}x-3\text{.}$ Обратите внимание на соотношение между их наклонами: $-3=-\frac{ 1}{\sfrac{1}{3}}$Рисунок 4.8.26. Графики $y=x$ и \(y=-x\text{.

}\) Обратите внимание на соотношение между их наклонами: $1=-\frac{1}{-1}$

Пример 4.8.27.

Объяснение

Мы будем использовать формулу наклона, чтобы найти наклоны обеих линий:

Их наклоны неодинаковы, поэтому эти две линии не параллельны.

Произведение их наклонов равно $(-4)\cdot\frac{1}{4}=-1\text{,}\text{,}$, что означает, что две линии перпендикулярны.

КПП 4.8.28.

Упражнения 4.

8.4 Упражнения

Обзор и прогрев

1.

Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).

$\displaystyle{ \frac{0}{2} = }$
$\displaystyle{ \frac{2}{0} = }$

2.

Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).

$\displaystyle{ \frac{3}{0} = }$
$\displaystyle{ \frac{0}{3} = }$

3.

Прямая проходит через точки $(4,-4)$ и $(-5,-4)\text{.}$ Найдите наклон этой линии.

4.

Прямая проходит через точки $(2,-1)$ и $(-3,-1)\text{.}$ Найдите наклон этой линии.

5.

Прямая проходит через точки $(1,-1)$ и $(1,5)\text{.}$ Найдите наклон этой линии.

6.

Прямая проходит через точки $(3,-3)$ и $(3,3)\text{.}$ Найдите наклон этой линии.

7.

Рассмотрим уравнение:

\begin{уравнение*} у=1 \end{уравнение*}

$\displaystyle (1,3)$
$\displaystyle (-9,1)$
$\displaystyle (8,1)$
$\displaystyle (0,10)$

8.

Рассмотрим уравнение:

\begin{уравнение*} у=1 \end{уравнение*}

$\displaystyle (-2,1)$
$\displaystyle (1,6)$
$\displaystyle (9,1)$
$\displaystyle (0,7)$

9.

Рассмотрим уравнение:

\begin{уравнение*} х+1=0 \end{уравнение*}

$\displaystyle (1,-1)$
$\displaystyle (0,-7)$
$\displaystyle (-1,0)$
$\displaystyle (-1,5)$

10.

Рассмотрим уравнение:

\begin{уравнение*} х+1=0 \end{уравнение*}

$\displaystyle (-1,1)$
$\displaystyle (-1,0)$
$\displaystyle (0,-9)$
$\displaystyle (1,-1)$

Столы для горизонтальных и вертикальных линий

11.

Заполните эту таблицу для уравнения $y=3\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-3$	$3$	$\влево(-3,3\вправо)$
$-2$
$-1$
$0$
$1$
$2$

12.

Заполните эту таблицу для уравнения $y=4\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-3$	$4$	$\влево(-3,4\вправо)$
$-2$
$-1$
$0$
$1$
$2$

13.

Заполните эту таблицу для уравнения $x=-6\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-6$	$-3$	$\влево(-6,-3\вправо)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

14.

Заполните эту таблицу для уравнения $x=-5\text{.}$ Первая строка является примером.

$х$	$у$	Очки
$-5$	$-3$	$\влево(-5,-3\вправо)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

Линейные уравнения

15.

Прямая проходит через точки $(-1,3)$ и $(-4,3)\text{.}$ Найдите уравнение для этой прямой.

16.

Прямая проходит через точки $(-4,6)$ и $(1,6)\text{.}$ Найдите уравнение для этой прямой.

17.

Прямая проходит через точки $(8,3)$ и $(8,5)\text{. }$ Найдите уравнение для этой прямой.

18.

Прямая проходит через точки $(10,-1)$ и $(10,-4)\text{.}$ Найдите уравнение для этой прямой.

19.

Показан линейный график. Напишите уравнение прямой.

20.

Показан линейный график. Напишите уравнение прямой.

21.

Показан линейный график. Напишите уравнение прямой.

22.

Показан линейный график. Напишите уравнение прямой.

Перехваты

23.

\begin{уравнение*} х = 1 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

24.

\begin{уравнение*} х = 3 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

25.

\begin{уравнение*} у = 5 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

26.

\begin{уравнение*} у = 8 \end{уравнение*}

	$х$-значение	$y$-значение	Местоположение
$y$-перехват
$х$-перехват

Графики горизонтальных и вертикальных линий

27.

Нарисуйте линию $y=1\text{.}$

28.

Нарисуйте линию $y+5=0\text{.}$

29.

Нарисуйте линию $y-6=0\text{.}$

30.

Нарисуйте линию $x=2\text{.}$

31.

Нарисуйте линию $x+4=0\text{.}$

32.

Нарисуйте линию $x-3=0\text{.}$

Параллельно или перпендикулярно?

33.

Линия $m$ проходит через точки $(-4,-25)$ и $(1,0)\text{.}$

Линия $n$ проходит через точки $(1,-4)$ и $(5,16)\text{.}$

Эти две строки

34.

Линия $m$ проходит через точки $(-9,4)$ и $(-27,8)\text{.}$

Линия $n$ проходит через точки $(9,-11)$ и $(-18,-5)\text{.}$

Эти две строки равны

35.

Линия $m$ проходит через точки $(6,-1)$ и $(-6,5)\text{.}$

Линия $n$ проходит через точки $(1,-8)$ и $(2,-6)\text{.}$

Эти две строки

36.

Линия $m$ проходит через точки $(6,-10)$ и $(-9,10)\text{.}$

Линия $n$ проходит через точки $(8,-3)$ и $(-8,-15)\text{.}$

Эти две строки равны

37.

Линия $m$ проходит через точки $(4,-4)$ и $(-5,23)\text{.}$

Линия $n$ проходит через точки $(1,10)$ и $(-3,-2)\text{.}$

Эти две строки

38.

Линия $m$ проходит через точки $(1,1)$ и $(-5,1)\text{. }$

Линия $n$ проходит через точки $(10,-5)$ и $(-9,-5)\text{.}$

Эти две строки

39.

Линия $m$ проходит через точки $(3,-6)$ и $(3,3)\text{.}$

Линия $n$ проходит через точки $(10,10)$ и $(10,1)\text{.}$

Эти две строки

40.

Линия $m$ проходит через точки $(5,7)$ и $(5,-9)\text{.}$

Линия $n$ проходит через точки $(4,10)$ и $(4,-10)\text{.}$

Эти две строки

Уравнения параллельных и перпендикулярных линий

41.

Прямая проходит через точку $(-2,0)\text{,}$ и параллельна прямой $y=8\text{.}$ Найдите уравнение для этой прямой.

42.

Прямая проходит через точку $(9,-7)\text{,}$ и она параллельна прямой $y=10\text{.}$ Найдите уравнение для этой прямой.

43.

Прямая проходит через точку $(6,-4)\text{,}$ и параллельна прямой $x=-9\text{.}$ Найдите уравнение для этой прямой.

44.

Прямая проходит через точку $(-1,5)\text{,}$ и параллельна прямой $x=-6\text{.}$ Найдите уравнение для этой прямой.

45.

Линия $k$ и линия $\ell$ параллельны.

Строка $k$ имеет уравнение $y=3x+3\text{.}$

Линия $\ell$ проходит через точку $(-5,-11)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме пересечения наклона равна

46.

Линия $k$ и линия $\ell$ параллельны.

Строка $k$ имеет уравнение $y=4x+5\text{.}$

Линия $\ell$ проходит через точку $(4,15)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме точки пересечения

47.

Линия $k$ и линия $\ell$ параллельны.

Строка $k$ имеет уравнение $y=-\frac{1}{3}x+8\text{.}$

Линия $\ell$ проходит через точку $(-9,7)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Строка $\ell$ в форме пересечения наклона равна

48.

Линия $k$ и линия $\ell$ параллельны.

Строка $k$ имеет уравнение $y=-\frac{2}{7}x-7\text{.}$

Линия $\ell$ проходит через точку $(14,1)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме пересечения наклона равна

49.

Линия $k$ и линия $\ell$ перпендикулярны.

Строка $k$ имеет уравнение $y=-x+5\text{.}$

Линия $\ell$ проходит через точку $(-3,1)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме пересечения наклона равна

50.

Линия $k$ и линия $\ell$ перпендикулярны.

Строка $k$ имеет уравнение $y=-3x-4\text{.}$

Прямая $\ell$ проходит через точку $\left(2,-\frac{7}{3}\right)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме пересечения наклона равна

51.

Линия $k$ и линия $\ell$ перпендикулярны.

Строка $k$ имеет уравнение $y=\frac{5}{8}x+5\text{.}$

Линия $\ell$ проходит через точку $\left(-2,\frac{36}{5}\right)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Линия $\ell$ в форме пересечения наклона равна

52.

Линия $k$ и линия $\ell$ перпендикулярны.

Строка $k$ имеет уравнение $x-5y=-25\text{.}$

Линия $\ell$ проходит через точку $(3,-13)\text{.}$

Найдите уравнение для линии $\ell$ как в форме точки-наклона, так и в форме наклона-пересечения.

Линия $\ell$ в форме точка-наклон равна

Строка $\ell$ в форме пересечения наклона равна

Вызов

53.

Нейронная основа суждений о делении пополам по вертикальной и горизонтальной линиям: фМРТ-исследование здоровых добровольцев

. 2001 г., июль; 14 (1 часть 2): S59-67.

doi: 10.1006/nimg.2001.0819.

Г Р Финк ¹ , J C Marshall, P H Weiss, K Zilles

принадлежность

¹ Медицинский институт, Исследовательский центр Юлиха, Юлих, 52425, Германия. [email protected]

PMID: 11373134
DOI: 10.1006/нимг.2001.0819

GR Fink et al. Нейроизображение. 2001 июль

. 2001 г., июль; 14 (1 часть 2): S59-67.

doi: 10.1006/nimg.2001.0819.

Авторы

Г Р Финк ¹ , Дж. К. Маршалл, П. Х. Вайс, К. Зиллес

принадлежность

¹ Медицинский институт, Исследовательский центр Юлиха, Юлих, 52425, Германия. [email protected]

PMID: 11373134
DOI: 10.1006/нимг.2001.0819

Абстрактный

Разделение горизонтальных линий пополам используется в качестве клинического теста пространственного познания у пациентов с игнорированием левого зрительно-пространственного восприятия после поражений правого полушария. Разделение вертикальных линий пополам также использовалось, хотя и реже. Интересно, что нормальные объекты часто делят горизонтальные линии слишком далеко влево, а вертикальные — слишком высоко. Мы использовали фМРТ, чтобы выяснить, взаимодействует ли вертикальная/горизонтальная ориентация стимула с нейронными механизмами, связанными с суждениями о делении линии пополам (задача Landmark). Для контроля ориентации как таковой испытуемые выполняли задачу визуального обнаружения с теми же стимулами. Статистический анализ вызванных ответов BOLD с использованием SPM99. Задача Landmark увеличила нервную активность (P < 0,05, скорректировано) в верхней и нижней теменных долях с двух сторон, хотя преимущественно справа; зоны ранней зрительной обработки двусторонне; и червь мозжечка, левое полушарие мозжечка, передняя поясная извилина и префронтальная кора с двух сторон. Вертикальные линии (по сравнению с горизонтальными линиями и наоборот) увеличивали нейронную активность в областях ранней обработки зрительной информации, что согласуется с дифференциальной ретинотопической стимуляцией. Кроме того, вертикальные линии билатерально активировали правую теменно-затылочную и верхнюю заднюю теменную кору. Никаких существенных взаимодействий между нервными механизмами, связанными с заданием и стимулами, не наблюдалось. Повышенная нервная активация в теменной и теменно-затылочной коре, связанная с вертикальными линиями, может отражать повышенные требования к вниманию, связанные с этой ориентацией стимула. Доминирование правого полушария, наблюдаемое в задней теменной области во время задания Landmark, независимо от ориентации стимула, согласуется с исследованиями поражений. Наши результаты показывают, что поведенческие паттерны, наблюдаемые у нормальных субъектов и неврологических пациентов, являются результатом различных эффектов стимула, а не различных требований к задаче.

Цитируется

Односторонняя катодная транскраниальная стимуляция постоянным током над теменной областью модулирует постуральный контроль в зависимости от открытых и закрытых глаз.
Ока С., Икеда Т., Мицутакэ Т., Огата К., Гото Ю. Ока С. и др. ПЛОС Один. 2022, 22 сентября; 17(9):e0269145. doi: 10.1371/journal. pone.0269145. Электронная коллекция 2022. ПЛОС Один. 2022. PMID: 36137124 Бесплатная статья ЧВК.
Модулирует ли рука изменение формы системы внимания во время адаптации правой призмы? ФМРТ-исследование.
Фаррон Н., Кларк С., Кроттаз-Хербетт С. Фаррон Н. и др. Фронт Псих. 2022 27 июля; 13:5. doi: 10.3389/fpsyg.2022.5. Электронная коллекция 2022. Фронт Псих. 2022. PMID: 35967619 Бесплатная статья ЧВК.
Выбор сторон: влияние призматической адаптации на латерализацию системы внимания.
Кларк С., Фаррон Н., Кроттаз-Хербетт С. Кларк С. и др. Фронт Псих. 2022 23 июня; 13:6. doi: 10.3389/fpsyg.2022.6. Электронная коллекция 2022. Фронт Псих. 2022. PMID: 35814089 Бесплатная статья ЧВК.

\(х\)	\(у\)
\(5\)	\(-6\)
\(5\)	\(-2\)
\(5\)	\(1\)
\(5\)	\(5\)

\(у\)	\(х+0у=5\подразумевается х=5\)	Заказанная пара
\(-6\)	\(х+0(-6)=5\подразумевается х=5\)	\((5,-6)\)
\(-2\)	\(х+0(-2)=5\подразумевается х=5\)	\((5,-2)\)
\(1\)	\(х+0(1)=5\подразумевается х=5\)	\((5,1)\)
\(5\)	\(х+0(5)=5\подразумевается х=5\)	\((5,5)\)

Горизонтальные линии	Вертикальные линии
Линия является горизонтальной тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение} у=к \end{уравнение} для некоторой константы \(k\text{.}\)	Линия вертикальна тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение} х=ч \end{уравнение} для некоторой константы \(h\text{. }\)
В стандартной форме (3.7.1) любая строка с уравнением \begin{уравнение} 0x+By=С \end{уравнение} горизонтальный.	В стандартной форме (3.7.1) любая строка с уравнением \begin{уравнение} Ах+0у=С \end{уравнение} вертикальный.
Если линия с уравнением \(y=k\) горизонтальна, она имеет точку пересечения \(y\) в точке \((0,k)\) и наклон \(0\text{.} \)	Если линия с уравнением \(x=h\) вертикальна, она имеет точку пересечения \(x\) в точке \((h,0)\) и ее наклон равен не определено . Одни говорят, что у него , а не наклон, а другие говорят, что наклон бесконечно большой .
В форме пересечения наклона (3.5.1) любая линия с уравнением \begin{уравнение} у=0х+б \end{уравнение} горизонтальный.	Невозможно записать уравнение вертикальной линии в форме пересечения наклона (3. 5.1), поскольку вертикальные линии не имеют определенного наклона.

\(х\)	\(у\)	Очки
\(-3\)	\(8\)	\(\влево(-3,8\вправо)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)

\(х\)	\(у\)	Очки
\(-3\)	\(9\)	\(\влево(-3,9\вправо)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)

	\(х\)-значение	\(y\)-значение	Местоположение
\(y\)-перехват
\(х\)-перехват

\(х\)	\(у\)
\(-4\)	\(7\)
\(10\)	\(-5\)

#1 Прямые линии — вертикали и горизонтали :: DIY Photo School

Линии

Горизонтальные линии

Вертикальные линии

Горизонталь или вертикаль: какую карьеру выбрать?

Вертикали и горизонтали в картинах мира Текст научной статьи по специальности «Языкознание и литературоведение»

Вертикаль и Горизонталь Андрея Тарковского » Философия вертикали+горизонтали. Константин Рылёв. Блог-книга на Peremeny.ru

Вертикали и горизонтали

Выставка «Вертикаль – Горизонталь: Рихард Пауль Лозе – Владимир Андреенков» в Музее архитектуры им. Щусева. 25.09 – 4.10.2019

Richard Paul Lohse. 15 systematic color series. 1950/62

Открытие выставки «Вертикаль. Горизонталь»

Владимир Андреенков. 4 красных вертикали. 1984/2002

Владимир Андреенков. Созвучия No43. 1991

Владимир Андреенков. Созвучия No44. 1991

Владимир Андреенков. Созвучия No45. 1991

Владимир Андреенков. Созвучия No46.

Владимир Андреенков. Две голубые вертикали No1. 1971

Владимир Андреенков. Две голубые вертикали No2. 1971

Владимир Андреенков. Две голубые вертикали No3. 1971

Владимир Андреенков. Две вертикали 1971-2002

Владимир Андреенков. Красная вертикаль 1972-2002

Richard Paul Lohse. Interpenetration of two color progressions

Richard Paul Lohse. Interpenetration of two color progressions

Richard Paul Lohse. Progression from yellow to violet

Richard Paul Lohse. Interpenetration of five color progressions

Richard Paul Lohse. Interpenetration of four color progressions

Richard Paul Lohse.

Richard Paul Lohse. Interpenetration of four color progressions

Richard Paul Lohse. Interpenetration of four color progressions

Richard Paul Lohse. Interpenetration of five color progressions

Владимир Андреенков. Вариации на тему пространства. 1970

Владимир Андреенков. Вертикали. 1972

Владимир Андреенков на открытии выставки

Выравнивание текста или настройка границ в текстовом поле

Выравнивание текста по горизонтали

Выравнивание текста по вертикали

Настройка полей надписи

Выравнивание текста по горизонтали

Выравнивание текста по вертикали

Настройка полей надписи

горизонтальных и вертикальных линий | Purplemath

Purplemath

MathHelp.com

ORCCA Горизонтальные, вертикальные, параллельные и перпендикулярные линии

Цели: Содержание курса PCC и руководство по результатам

Подраздел 3.8.1 Горизонтальные линии и вертикальные линии

Пример 3.8.6.

Пример 3.8.8.

Пример 3.

КПП 3.8.11. Точки построения.

Пример 3.8.12. Наклон вертикальной линии.

Факт 3.8.14.

КПП 3.8.16. Точки построения.

Пример 3.8.17.

Подраздел 3.8.2 Параллельные линии

Пример 3.8.20.

Факт 3.8.22.

КПП 3.8.23.

КПП 3.8.24.

Подраздел 3.8.3 Перпендикулярные линии

Факт 3.8.26.

Пример 3.8.30.

КПП 3.8.31.

Вопросы для чтения 3.8.4 Вопросы для чтения

1.

2.

3.

Упражнения 3.8.5 Упражнения

Обзор и прогрев

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.