#1 Прямые линии — вертикали и горизонтали :: DIY Photo School
Итак, поехали!
Речь в первом выпуске пойдёт о вертикальных и горизонтальных линиях.
Я постарался сохранить основной смысл, немного сократив исходные тексты и по-возможности упростив описание. Если всё же встретите незнакомые слова, спросите в комментариях, особенно если это мешает понять идею. Ничего зазорного в этом нет, мы все тут новички.
Настоятельно рекомендую пойти и почитать сами источники, особенно Майкла Фримана (ссылки в конце поста). Это займёт 10-30 минут. Некоторые мысли и идеи, а главное авторские иллюстрации, не попали в выпуск.
P.S: Картинки в посте видно?
Линии
Все изображения состоят из совокупности линий, форм и очертаний. В фотографии линии проявляются менее явно, чем в изобразительном искусстве, и обычно они воображаемые. Роль линии часто играют края видимых предметов или последовательность объектов.
При визуальном определении линий наибольшую роль играет контраст — между светом и тенью, участками разного цвета, текстурами и формами. Поскольку рамка фотографии сама состоит из линий, это побуждает глаз сравнивать угол и длину линий рамки и линий изображения.
Линии характеризуются динамическими свойствами — направлением и движением. С помощью линий, автор может направлять взгляд зрителя по пространству кадра к объекту.
Линии обладают и выразительными свойствами. Мощные чёткие линии могут выражать смелость, тонкие изгибающиеся линии намекают на деликатность и т.д.
Разные формы линий вызывают определённые ассоциации. Горизонтальные и вертикальные линии порождают ощущение силы и мощи и некой статичности. Диагональные линии создают впечатление движения неподвижного изображения.
Горизонтальные, вертикальные и наклонные линии (диагонали), вносят свой вклад в создание настроения, вызываемого изображением. Угол наклона и соотношение с размером рамки определяют влияние линии на восприятие изображения.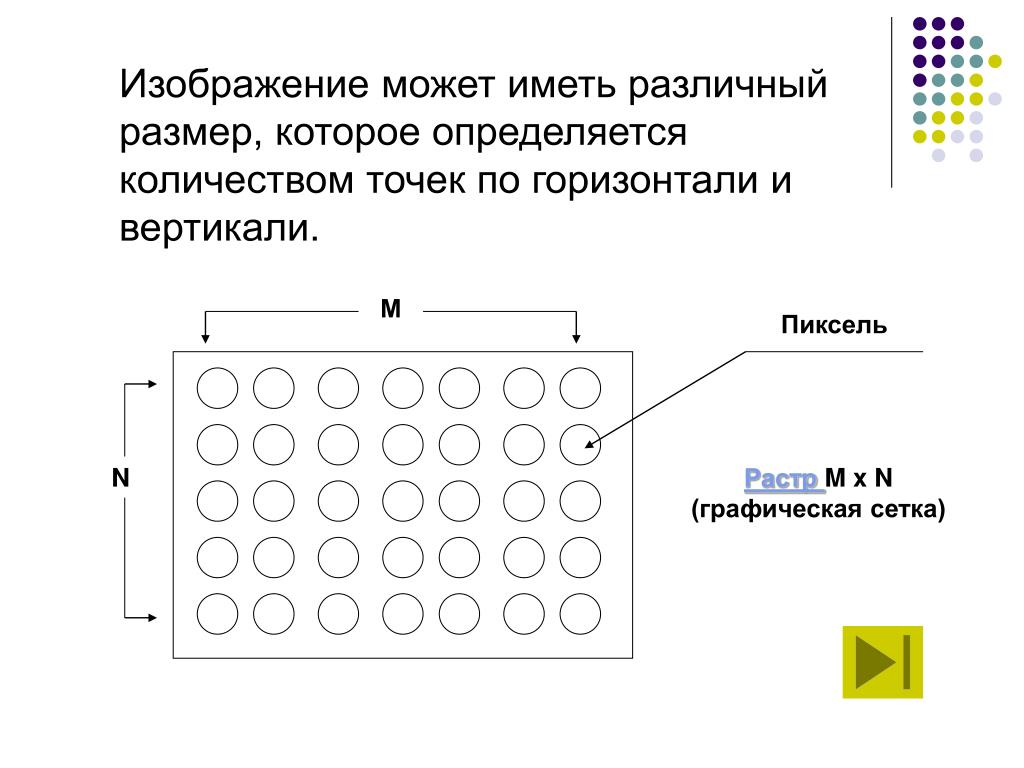 Большое влияние имеют тон и цвет линии по отношению к остальному изображению, а также её повторяемость.
Большое влияние имеют тон и цвет линии по отношению к остальному изображению, а также её повторяемость.
Как и любой приём, линии могут помочь создать или наоборот разрушить образ.
Горизонтальные линии
Горизонталь во многих смыслах служит базовой линией композиции. Это фундаментальная ориентирная линия, самая знакомая из всех, и даже её визуальная тяжесть — это напоминание о том, что горизонтальная поверхность есть держащая основа. Поэтому горизонтальные линии обычно выражают стабильность, вес, мир и спокойствие. Через их ассоциацию с горизонтом они также указывают на дистанцию и широту.
Прямые горизонтальные линии могут играть роль разделительной черты, заставляющей зрителя оставаться снаружи, заглядывая за них.
Горизонтали практически всегда присутствуют в перспективном изображении. Даже беспорядочные скопления объектов с увеличением дистанции превращаются в горизонтальные вереницы предметов, и в конченом итоге — в линии.
Вертикальные линии
Вертикаль — второй основной компонент рамки.
Для единичной вертикали более подходит вертикальный формат. Однако группа вертикальных форм может служить основой горизонтального кадра.
Вертикальная линия обычно является главным компонентом изображения человеческой фигуры или дерева. Её направление совпадает с направлением вектора силы тяжести или противоположно ему.
Без ассоциации с поддерживающей основой, характерной для горизонтальной линии, вертикальная линия обычно в большей степени даёт ощущение скорости и движения — либо вверх, либо вниз.
Видимые отвесно с низкой точки съёмки вертикали при подходящих обстоятельствах словно противостоят зрителю. Изображение содержащее выраженные вертикальные линии как правило вызывает ощущение высоты и значительности.
Несколько вертикальных форм могут вызывать ассоциации с барьером — например, столбы или шеренга людей, стоящих лицом к объективу. В какой-то степени они могут олицетворять силу и власть.
Как и в случае с горизонтальными линиями, здесь очень важно выравнивание. На фотографии и те и другие сразу сопоставляются взглядом с краями рамки, и даже незначительное несоответствие моментально бросается в глаза.
Горизонтальные и вертикальные линии перпендикулярны и действуют как ограничители друг друга, уравновешивая композицию. Также они могут создавать ощущение баланса, так как возникает ассоциация с прямым стоянием, поддерживаемым на плоской поверхности.
Композиция, основанная на вертикальных и горизонтальных линиях вызывает ощущение надёжности, удовлетворения.
Материал возмутительным образом скопирован из:
Майкл Фриман. Дао цифровой фотографии (pdf)
Эксель, Бетдорф и др. Искусство фотографии: сила композиции (pdf)
wikipedia.org: Composition_(visual_arts)
Иллюстрации, на мой взгляд, подобраны не сильно удачно, но общую идею вроде удалось показать.
Добро пожаловать в комментарии, там можно обсудить описание, задания и способности автора 🙂
Также категорически приветствуется обсуждение всего что касается выполнения задания, непонятных моментов и прочего. Это едва ли не главное, ради чего стоит обучаться вместе!
Это едва ли не главное, ради чего стоит обучаться вместе!
Спасибо за внимание!
Задания к выпуску
Другая сторона практики — пересмотрите любимые работы фотографов и живописцев. Обратите внимание, как используются описанные приёмы. Поделитесь вдохновением с соучастниками 🙂
Вертикали и горизонтали. Тайны древних цивилизаций. Том 2 [Сборник статей]
Вертикали и горизонтали
Возможно, за всю историю Европы именно в готическом храме полнее всего выразилась идея культуры как пути к Божеству. Собор – не застывшее отражение божественного величия и мощи, а подвижное, живое во многом благодаря никогда не стоящему на месте свету отражение пути человека к Богу. Пути от света земного к свету Божественному. С запада на восток, где сияет над алтарем образ Христа – Солнца Справедливости. Пути от болезни к здоровью, «пути исцеления», как называли в Средние века центральный неф.
Что представлял собой готический собор? В основе его плана – базилика, роднящая готику с раннехристианскими храмами, строившимися по модели римского дома для собраний. Его пространство – три, реже пять нефов: один главный, центральный, и боковые. Главный неф (от слова nave – «корабль») – ось собора, протянувшаяся с запада на восток, от царства мрака навстречу восходящему солнцу. Высотой нефа измерялась высота собора, благодаря ей создавалось ощущение вертикальности, устремленности вверх. Она поражала входившего в храм. Строители пытались вознести свод как можно выше. Собор в Бове, пока его строили, обрушивался два раза – мечты архитекторов обгоняли их возможности. Тем не менее, сейчас это один из самых высоких готических храмов, высота его сводов 47 метров (почти 20 этажей современного дома). Длина нефа до 150 метров – поистине путь!
Его пространство – три, реже пять нефов: один главный, центральный, и боковые. Главный неф (от слова nave – «корабль») – ось собора, протянувшаяся с запада на восток, от царства мрака навстречу восходящему солнцу. Высотой нефа измерялась высота собора, благодаря ей создавалось ощущение вертикальности, устремленности вверх. Она поражала входившего в храм. Строители пытались вознести свод как можно выше. Собор в Бове, пока его строили, обрушивался два раза – мечты архитекторов обгоняли их возможности. Тем не менее, сейчас это один из самых высоких готических храмов, высота его сводов 47 метров (почти 20 этажей современного дома). Длина нефа до 150 метров – поистине путь!
Боковые нефы были, как правило, существенно ниже центрального, поэтому путь этот освещался светом, лившимся из огромных витражных окон верхнего яруса. Подобно величественному кораблю – ковчегу, собор плыл вместе с вращением Земли навстречу восходящему солнцу среди суеты повседневной жизни.
Ближе к восточной стороне неф пересекался трансептом, образуя громадный крест – символ духа, распятого в материи. Символ жертвы ради любви и сострадания к человеку. Над центром креста, символически над сердцем распятого Божества, возвышалась башенка, а под ним в крипте находился колодец, образуя еще одну ось – вертикальную, соединявшую небо и землю.
Символ жертвы ради любви и сострадания к человеку. Над центром креста, символически над сердцем распятого Божества, возвышалась башенка, а под ним в крипте находился колодец, образуя еще одну ось – вертикальную, соединявшую небо и землю.
Алтарь располагался в восточной части собора, в центре хора, окруженный так называемым деамбулаторием, обходом вокруг. Этого обхода нет в православных храмах.
Троица в витраже: свет – Отец, материя стекла – Дух Святой, священные образы человека и природы – Сын
Часовня Сен-Шапель в Париже
Собор – отражение Космоса, в котором живет человек. Его своды покрывались звездами и становились подобны высокому ночному небу. Колонны храма символизировали деревья, пол – землю. Его стены и окна благодаря стрельчатой форме арок устремлялись ввысь, задавая основные вектора движения – к востоку по горизонтали и к Небу по вертикали.
Но что интересно, похожее строение имели, например, египетские храмы Нового царства и храмы Древней Индии, где святилище было окружено коридором или даже двумя.
Горизонталью по вертикали
Горизонталью по вертикали 6 февраля, 11:38Многие возражают против моего предложения выступить 4 марта единым фронтом. Из этого делаю вывод, что я плохо объяснил идею.Несколько уточнений вдогонку.1. Сейчас речь идет только о том, чтобы мы в принципе договорились действовать
«Период полураспада»: погром вертикали власти
«Период полураспада»: погром вертикали власти
Генеральный секретарь ЦК КПССЗахватить этот пост — задача номер один. Потом разрушающая волна на уровне всего Союза и всей партии пойдет отсюда.«…высшая власть в стране принадлежала Генсеку — „царю и богу“, по известному
Потом разрушающая волна на уровне всего Союза и всей партии пойдет отсюда.«…высшая власть в стране принадлежала Генсеку — „царю и богу“, по известному
201. Тупик непарламентской оппозиции. Растление идет по вертикали из центра на места
201. Тупик непарламентской оппозиции. Растление идет по вертикали из центра на места — Говоря по-честному, не вижу, чем откорректировать развернувшийся по всей стране процесс захвата и присвоения власти. Здесь нужна прямая политическая борьба, прямое действие, а от этого
Глава 7 Федерация. Построение вертикали власти
Глава 1 Китай: экспансия «по вертикали»; Индия: экспансия «по горизонтали»
Глава 1
Китай: экспансия «по вертикали»; Индия: экспансия «по горизонтали»
Аль-Бахр-аль-Хинди – так назывался этот океан в древних арабских трактатах о мореходстве. Индийский океан и водные потоки, впадающие в него, поныне хранят привкус той великой, стремившейся
Индийский океан и водные потоки, впадающие в него, поныне хранят привкус той великой, стремившейся
Горизонтали и вертикали. Код Мандельштама
Горизонтали и вертикали
Жизнь человека — поиск, отягченный незнанием будущего.
Единственно, что знает каждый, — конечный исход этого поиска, называемый смертью. Если поиск ведется в кромешной тьме и человек лишен возможности отыскать на шкале жизни то место, где он находится, поневоле ориентиром становится крайняя точка.
Но значит ли это, что данную точку ищущий считает спасением?
И значит ли это, что следует отвергать поиск как таковой, значит ли это, что жизнь отвращает от себя уже самим обозначением конечного ориентира? Углубившись в раздумья на эту тему, начинаешь замечать, что ищущие тоже устроены по-разному: для кого-то поиск — движение по горизонтали:
назад — вперед
а для кого-то — это низвержение и вознесение: вверх — вниз.
Поэт Мандельштам, безусловно, относится к тем, кому дано в своем поиске подняться на необозримую высоту и низвергнуться глубоко вниз.
И заметим, что смерть для него — низвержение.
Психея-жизнь
Но вот что проявляется в двадцатых годах: если раньше поэт говорил о ночи в отправной точке и выше, поскольку в той его ночи царило черно-желтое солнце, он наблюдал за ней как бы снизу вверх, то сейчас все чаще НОЧЬ отождествляется с тем, что внизу!
Постепенное уступание смерти?
Она берет тех, кто с нею внутренне смирился.
Мандельштам — пока нет.
Но слишком часты эти вылазки в мир теней, в котором он пока (как Персефона) проводит лишь часть отпущенного ему времени, но возвращается в него снова и снова «на крыльях срезанных», чтобы играть с прозрачными тенями, среди бесплотных мыслей, вернувшихся «в чертог теней» («Я слово позабыл, что я хотел сказать…»).
И все же несмирение со смертью, стремление ввысь отчетливо видно в желании поэта «разбудить ночь»:
Я хотел бы ни о чем
Еще раз поговорить,
Прошуршать спичкой, плечом
Растолкать ночь — разбудить.
Приподнять, как душный стог,
Воздух, что шапкой томит.
Перетряхнуть мешок,
В котором тмин зашит,
Чтобы розовой крови связь,
Этих сухоньких трав звон,
Уворованная нашлась
Через век, сеновал, сон.
(«Я не знаю, с каких пор…», 1922)
Растолкать душную ночь, сбросить давящую тяжесть — впрочем, нет, не сбросить, но хоть чуть-чуть ослабить — приподнять, восстановить кровную связь с небом, найти место обрыва этой связи.
Тут порыв (но не прорыв!) сквозь шапку воздуха.
Душа устремлена к небу.
Мечта о ночи-жизни выражается в желании «растолкать ночь». Спящая ночь — ночь-смерть.
Это стремление ввысь видим и в следующем стихотворении (опубликованном поэтом вместе со стихотворением «Я не знаю, с каких пор…»).
Я по лесенке приставной
Лез на всклоченный сеновал,
Я дышал звезд млечных трухой,
Колтуном пространства дышал.
Там, высоко-высоко, пространство, откуда выброшен в жизнь поэт.
В жизнь, пересекающую его связь с небом, звездами.
Распряженный огромный воз
Поперек вселенной торчит…
Именно этот воз, груженный кошмарами жизни, разрывает «розовой крови связь» поэта с высью, и дальше потрясающе емкая формула, определяющая причины разлада с тем, что здесь:
Не своей чешуей шуршим,
Против шерсти мира поем.
Лиру строим, словно спешим
Обрасти косматым руном.
Мир видится Мандельштаму зверем, ибо шерсть — волос животного (такое толкование приводит В. Даль как самое первое).
Гладить против шерсти — доставлять неудовольствие, раздражать, дразнить.
В этой метафоре явно обозначено противопоставление себя миру, не-кровность связи с этим миром-зверем.
«Мать гладит по шерсти, мачеха супротив» — такую поговорку находим у Даля.
В данном случае раздражающее, провоцирующее действие производит не мачеха, а пасынок.
Пасынок жизни, каковым поэт ощущает себя очень давно, ибо внутренняя не-родственность певца, дышащего «колтуном пространства», с вечной склокой древнего сеновала жизни, ощущающаяся под гнетом внешних обстоятельств все более, прослеживается с самого начала творчества О. Мандельштама.
Мандельштама.
Направление роста шерсти — вниз. Поэт поет «против шерсти». Не для того, чтобы просто раздразнить, взбудоражить — он устремлен ввысь, к звездам. Так устроена его лира. Мир не пускает, тянет назад, эти пространственные колебания (по вертикали) наполняют все стихотворение.
В следующей строфе — та же картина (с точки зрения этого «вниз — вверх»):
Из гнезда упавших щеглов
Косари приносят назад,
Из горящих вырвусь рядов
И вернусь в родной звукоряд.
Падение из гнезда — сверху вниз.
В жизнь. Гнездо поэта — среди «трухи млечных звезд»? Кто эти «косари», возвращающие птенцов в родное гнездо, вверх?
Быть может, какая-то виденная сельская картинка складывается в трагический и одновременно спасительный образ смерти: какой косарь спасет щегла-поэта, упавшего со страшной высоты в горящие ряды жизни?
Какой косарь поможет вернуться в родной звукоряд, к звездам?
Человек с косой — символизирующий смерть в европейской традиции.
Только этот косарь может сделать так, чтобы распростились «розовой крови связь // И травы сухорукий звон».
Стихотворение наполнено колебаниями — вверх-вниз. Это «вверх» поэта Мандельштама — начало и конец, причина и следствие: вверх, «против шерсти», потому что иначе не может. И когда зверь-мир не простит, стряхнет с себя в гибельный хаос мертвой травы, тогда остается еще один — последний — порыв вверх — в родное млечное гнездо, к звездам.
Помог бы только косарь!
Разбуженная тьма-ночь, набухая и звеня, зовет поэта к себе — домой, откуда когда-то, «как раковина без жемчужин», был он выброшен.
Следующее за этим стихотворение «Ветер нам утешенье принес…» (1922) углубляет основную тему двух предыдущих:
Ветер нам утешенье принес,
И в лазури почуяли мы
Ассирийские крылья стрекоз,
Переборы коленчатой тьмы.
И военной грозой потемнел
Нижний слой помраченных небес,
Шестируких летающих тел
Слюдяной перепончатый лес.
Есть в лазури слепой уголок,
И в блаженные полдни всегда,
Как сгустившейся ночи намек,
Роковая трепещет звезда.
И с трудом пробиваясь вперед
В чешуе искалеченных крыл,
Под высокую руку берет
Побежденную твердь Азраил.
Ветер приносит в качестве утешения — тьму.
Полуденные знойные лазурные небеса в слепом уголке таят намек сгустившейся ночи, делают видимой роковую трепещущую звезду.
Взгляд снизу вверх к спасительной звездной тьме (даже среди ясной лазури!), и снизу же (из царства мертвых?) пробивается вперед к небу Азраил (ангел смерти), стремительно, калеча крылья и побеждая небесную твердь.
НОЧЬ — ВЫСЬ — СМЕРТЬ — СПАСЕНИЕ (УТЕШЕНИЕ)
Вот итог этого поэтического цикла.
Данный текст является ознакомительным фрагментом.
Сбоку от вертикали
Сбоку от вертикали
«Внешняя среда» весны 2000 года ознаменовалась тем, что с первым теплом на российских просторах бурно пошли в рост не только привычные глазу озимые и сорняки, деревья и кустарники, но и растение, от которого народ слегка поотвык. Называется оно «властная
Называется оно «властная
От вертикали к горизонтали управления
От вертикали к горизонтали управления Трудности с подготовкой «честной» пятилетки окончательно убедили отца — министерская централизованная вертикальная структура себя исчерпала. Выход в регионализации экономики. Местные руководители, такие, как и он сам когда-то,
«Вертикаль» против «горизонтали»
«Вертикаль» против «горизонтали» 13 марта 1963 года происходит реорганизация правительства, создается Высший совет народного хозяйства СССР (ВСНХ) и одновременно резко укрупняются совнархозы. Их количество сокращается с первоначального (в 1957 году) почти полутораста до
Отношения с регионами. Реформа вертикали власти
Отношения с регионами. Реформа вертикали власти Еще 4 сентября в обращении к нации по поводу трагедии в Беслане Владимир Путин сказал, что в ближайшее время будет разработан комплекс мер по укреплению единства страны и народа и по созданию более эффективного контроля за
Гонки по вертикали
Гонки по вертикали
Не так уж сложно лазить по стенам, для этого достаточно иметь минимум знаний и немного тренировки. Привожу группу курсантов к невысокой каменной стене, полутораметровой высоты. Разбившись на пары, они должны, помогая друг другу, перелезть через нее.
Привожу группу курсантов к невысокой каменной стене, полутораметровой высоты. Разбившись на пары, они должны, помогая друг другу, перелезть через нее.
Авторитарное государство. Три вертикали Владимира Путина
Авторитарное государство. Три вертикали Владимира Путина 7 августа 2002 г. «Ведомости», МоскваВ конце июля заместитель руководителя администрации президента РФ г-н Д. Козак предложил поправку к закону о недрах, принятие которой могло бы кардинально изменить экономическую
Часть первая. ЧЕЛОВЕК ВЕРТИКАЛИ
Часть первая. ЧЕЛОВЕК ВЕРТИКАЛИ Я вижу то, что существует в жизни, чего не замечает
Глава третья По партийной «горизонтали»
Глава третья
По партийной «горизонтали»
Пензенский обком. ЦК Компартии Молдавии. Годы работы в агитпропе ЦК КПССПредписание Центрального комитета партии Пензенскому обкому было выполнено. В начале июня 1945 года К. У. Черненко был избран секретарем обкома партии по
Годы работы в агитпропе ЦК КПССПредписание Центрального комитета партии Пензенскому обкому было выполнено. В начале июня 1945 года К. У. Черненко был избран секретарем обкома партии по
Деление власти по вертикали и региональная горизонталь власти
Деление власти по вертикали и региональная горизонталь власти Деление власти по вертикали, иными словами, — между Федерацией и субъектами Федерации стало реальным достижением российской демократии, нашим наибольшим демократическим прорывом. В соответствии с
Глава 9 Спасение вертикали Провал на выборах
Глава 9
Спасение вертикали
Провал на выборах
Летом 1995 года, оценивая перспективы НДР, Борис Ельцин заявил: «На выборах в Государственную думу движение “Наш дом — Россия” наберет порядка 8-12 % голосов избирателей. Конечно, не 30–40 % и, естественно, не большинство». Это
Это
Отношения с регионами. Реформа вертикали власти
Отношения с регионами. Реформа вертикали власти Еще 4 сентября в обращении к нации по поводу трагедии в Беслане Владимир Путин сказал, что в ближайшее время будет разработан комплекс мер по укреплению единства страны и народа и по созданию более эффективного контроля за
Самоуправление: вертикаль вместо горизонтали
Самоуправление: вертикаль вместо горизонтали Реформа местного самоуправления стала одним из первых заметных политических шагов нового губернатора. При Рокецком – и это было предметом особой гордости – в области действовала поселенческая модель.Рокецкому, который
Выравнивание текста или настройка границ в текстовом поле
Word 2016 для Mac Word для Mac 2011 Еще… Меньше
Меньше
В Word текст надписи можно выравнивать по вертикали и по горизонтали, а также настраивать ширину полей. Горизонтальное выравнивание определяет расположение левого и правого краев абзаца между полями, а вертикальное — размещение текста между верхней и нижней границами.
Выравнивание текста по горизонтали
-
В надписи выделите текст, для которого нужно изменить выравнивание по горизонтали.
-
На вкладке Главная выберите нужный вариант выравнивания .
Выравнивание текста по вертикали
Вы можете выровнять весть текст в надписи по ее верхнему или нижнему краю либо по центру.
-
Щелкните внешнюю границу надписи, чтобы выделить ее.
-
На вкладке Формат фигуры щелкните Область форматирования.
-
Откройте вкладку Параметры фигуры, если она еще не выбрана.
-
Щелкните значок надписи и выберите пункт Надпись.
org/ListItem»>
Выберите По верхнему краю, По середине или По нижнему краю из раскрывающегося списка Выравнивание по вертикали.
Настройка полей надписи
-
Щелкните внешнюю границу надписи, чтобы выделить ее.
-
На вкладке Формат фигуры щелкните Область форматирования.
org/ListItem»>
-
Щелкните значок надписи и выберите пункт Надпись.
-
Вы можете настроить поля слева, справа, сверху и снизу.
Откройте вкладку Параметры фигуры, если она еще не выбрана.
Важно: Microsoft Office для Mac 2011 больше не поддерживается. Перейдите на Microsoft 365, чтобы работать удаленно с любого устройства и продолжать получать поддержку.
Обновить
Выравнивание текста по горизонтали
В надписи выделите текст, для которого нужно изменить выравнивание по горизонтали.
На вкладке Главная в области Абзацвыберите нужный вариант выравнивания .
Выравнивание текста по вертикали
Вы можете выровнять весть текст в надписи по ее верхнему или нижнему краю либо по центру.
-
Щелкните внешнюю границу надписи, чтобы выделить ее.
org/ListItem»>
-
Выберите требуемый вариант выравнивания.
Перейдите на вкладку Формат (сиреневую контекстную вкладку, которая появляется рядом с вкладкой Главная), а затем в области Текстовое поле щелкните Изменить выравнивание текста внутри .
Настройка полей надписи
-
Щелкните внешнюю границу надписи, чтобы выделить ее.
-
В меню Формат выберите пункт Фигура.

-
В левой области диалогового окна Формат фигуры нажмите кнопку Текстовое поле.
-
В разделе Внутренние поля настройте параметры расстояния между текстом и внешней границей надписи.
Выравнивание объектов
Настройка обтекания текстом объектов
Какое положение называется горизонтальным, что означает слово горизонталь
Горизонтальность, горизонталь, горизонтальный – все эти слова обозначают положение предмета или любого объекта, в том числе живого, описываемого в переносном смысле, по отношению к земле. Если посмотреть с некоторой дистанции на беспорядочное скопление предметов, то можно увидеть, что объекты превращаются в горизонтальные цепочки, в конченом итоге — в горизонтальные линии.
Если посмотреть с некоторой дистанции на беспорядочное скопление предметов, то можно увидеть, что объекты превращаются в горизонтальные цепочки, в конченом итоге — в горизонтальные линии.
…
Оглавление:
- Горизонтальная линия
- Горизонтальность, как психологическое понятие
- Горизонталь – топографическое определение
- Определение в профессиональном росте
Рассмотрим примеры, что значит по горизонтали?
- Мы смотрим вдаль – видим горизонт. Как расположена линия горизонта? Горизонтально. Чему? Земле.
- Мы легли отдыхать – приняли горизонтальное положение. В какой позиции находится наше тело? В горизонтальной. По отношению к чему? К дивану. К полу. К земле.
- Читаем письмо или книгу. Как расположены строки? По горизонтали. Относительно чего?
- Летит птица – горизонтально. Чему? Земле.
- Река течёт – горизонтально. Чему? Земле.
Здесь мы можем привести массу примеров, но теперь понятно, что горизонтальность означает параллельное положение линий, предметов, объектов или конструкций по отношению к земле или другому предмету (объекту, конструкции), но который должен быть расположен обязательно параллельно опять-таки земле. Чтобы было проще представить, что же такое горизонталь, горизонтальность или горизонт впредь предлагаем ориентироваться именно на расположение объекта по отношению в конечном счёте к поверхности земли.
Чтобы было проще представить, что же такое горизонталь, горизонтальность или горизонт впредь предлагаем ориентироваться именно на расположение объекта по отношению в конечном счёте к поверхности земли.
Это интересно: разность чисел — что это, как ее найти?
Горизонтальная линия
Рисуем горизонтальную линию на листе бумаги. Если лист бумаги лежит на столе – лист расположен горизонтально. Рисунок линии выполняется слева направо или справа налево – нарисована горизонтальная линия. Нарисовать на листе можно что угодно: вертикальные лини (сверху вниз или снизу вверх), диагональ, любой рисунок. При этом лист расположен всё равно горизонтально. Чему? Столу. Полу. Нижнему этажу дома. Земле.
Горизонталь – самая знакомая из всех, базовая линия. Она в каких угодно смыслах служит основой любой композиции. Даже её визуальная тяжесть напоминает о том, что горизонтальная поверхность есть фундаментальная держащая основа. Она параллельна земле. Не зря изображение горизонтальной линии выражает вес, спокойствие, мир и стабильность.
Она параллельна земле. Не зря изображение горизонтальной линии выражает вес, спокойствие, мир и стабильность.
Горизонтальность, как психологическое понятие
Горизонтальность линий в рисунках можно рассматривать через знание психологии. Прямые линии подразумевают некую разделительную черту. Человек, как зритель, может оставаться снаружи, заглядывая за неё, или перешагнуть этот горизонт, так сказать «переступить за черту». Прямые и чёткие линии выражают смелость и настойчивость, тонкие и изгибающиеся горизонтали – деликатность и мягкость.
Горизонталь – топографическое определение
Самое простое определение этому слову можно найти в многочисленных словарях и энциклопедиях разных направлений. Чаще всего такое название применяется в отношении изогипс, т. е., линий, соединяющих точки, находящиеся на одинаковой абсолютной высоте над уровнем моря или любой другой взятой за основу плоскости.
Вот как расшифровывает это понятие Энциклопедический толковый словарь И. А. Ефрона и Ф.А. Брокгауза:
А. Ефрона и Ф.А. Брокгауза:
- Горизонтали – (изогипсы) линии, соединяющие на местности точки, лежащие на одной и той же высоте над уровнем моря или какой-то основной плоскости, принятой за основание.
Вот что можно прочитать в Техническом железнодорожном словаре:
- Горизонтали – линии на карте или плане местности, полученные от пересечения земной поверхности горизонтальными плоскостями, стоящими друг от друга на одинаковом расстоянии.
Выдержка из Геологической энциклопедии:
- Горизонтали – это линии, соединяющие точки одной высоты над уровнем моря. С помощью горизонталей на топографических картах отображаются особенности рельефа различных участков земной коры.
И в конце приведём текст определения из Справочника технического переводчика (отрасль машиностроение):
- Горизонтали – линии на поверхности, параллельные горизонтальной плоскости проекций.
Определение в профессиональном росте
У профессионалов есть такое понятие, как вектор карьеры. Многочисленные и очень сейчас популярные тренинги по достижению результатов в профессиональной деятельности и продвижении по лестнице к успешной карьере, выносят на обсуждение идеи, которые подразумевают рост потенциала человека как по вертикали, так и по горизонтали. По вертикали понятно, перешагивая ступени одну за другой, т. е., двигаясь вверх, индивид поднимается по вертикали. А что со вторым вариантом?
Многочисленные и очень сейчас популярные тренинги по достижению результатов в профессиональной деятельности и продвижении по лестнице к успешной карьере, выносят на обсуждение идеи, которые подразумевают рост потенциала человека как по вертикали, так и по горизонтали. По вертикали понятно, перешагивая ступени одну за другой, т. е., двигаясь вверх, индивид поднимается по вертикали. А что со вторым вариантом?
Здесь надо вспомнить шутливый принцип канадского педагога Питера Лоуренса, говорящий о том, что при подъёме по вертикали есть предел, та ступень, выше которой человек подняться не в состоянии. Ну что ж, доля правды в этом есть. Но, мало кто согласен остановиться на том, в чём он хорош. Значит, есть смысл продолжить рост в другом направлении.
Рост по горизонтали означает углубление специалиста в экспертную область. Индивид становится отличным мастером и непревзойдённым экспертом в конкретном виде деятельности, конкретном направлении. Он делает свою работу, у него те же обязанности, но при этом освоены и применяются новые инструменты к выполнению возложенных задач. С некоторым временем его работа становится качественнее и выполняется виртуознее, за что профессионал больше ценится начальством и внешними партнёрами.
С некоторым временем его работа становится качественнее и выполняется виртуознее, за что профессионал больше ценится начальством и внешними партнёрами.
Другой вариант развития профессиональной деятельности по горизонтали – это переход в параллельное направление, приобретение в нём новых навыков, в том числе и во многих других областях. Это необходимо, когда в компании практикуют перестановку сотрудников из одного блока в другой. Например, из финансового отдела в логистику. С одной стороны, специалист вносит в это новое подразделение знания из других областей, с другой – учится всё время новому. Сотрудник сильно развивается личностно, что непременно скажется на его профессиональных качествах.
Многие профессионалы вполне остаются довольны ростом по горизонтали и не нуждаются в росте по вертикали, мотивируя это таким немаловажным бонусом, как меньшая ответственность. Самое главное, что в этом случае человек должен понять, в какой своей роли он будет наиболее успешен, ценен для профессии и эффективен для результата. Здесь надо хорошо продумать свои шаги по карьерной лестнице и быть честным с собой самим. Тем более что не все хотят быть руководителями.
Здесь надо хорошо продумать свои шаги по карьерной лестнице и быть честным с собой самим. Тем более что не все хотят быть руководителями.
Какое положение называется горизонтальным, что означает слово горизонталь
Горизонтальность, горизонталь, горизонтальный – все эти слова обозначают положение предмета или любого объекта, в том числе живого, описываемого в переносном смысле, по отношению к земле. Если посмотреть с некоторой дистанции на беспорядочное скопление предметов, то можно увидеть, что объекты превращаются в горизонтальные цепочки, в конченом итоге — в горизонтальные линии.
Оглавление:
- Горизонтальная линия
- Горизонтальность, как психологическое понятие
- Горизонталь – топографическое определение
- Определение в профессиональном росте
Рассмотрим примеры, что значит по горизонтали?
- Мы смотрим вдаль – видим горизонт.
 Как расположена линия горизонта? Горизонтально. Чему? Земле.
Как расположена линия горизонта? Горизонтально. Чему? Земле. - Мы легли отдыхать – приняли горизонтальное положение. В какой позиции находится наше тело? В горизонтальной. По отношению к чему? К дивану. К полу. К земле.
- Читаем письмо или книгу. Как расположены строки? По горизонтали. Относительно чего?
- Летит птица – горизонтально. Чему? Земле.
- Река течёт – горизонтально. Чему? Земле.
Здесь мы можем привести массу примеров, но теперь понятно, что горизонтальность означает параллельное положение линий, предметов, объектов или конструкций по отношению к земле или другому предмету (объекту, конструкции), но который должен быть расположен обязательно параллельно опять-таки земле. Чтобы было проще представить, что же такое горизонталь, горизонтальность или горизонт впредь предлагаем ориентироваться именно на расположение объекта по отношению в конечном счёте к поверхности земли.
Это интересно: разность чисел что это, как ее найти?
Содержание
Горизонтальная линия
Рисуем горизонтальную линию на листе бумаги. Если лист бумаги лежит на столе – лист расположен горизонтально. Рисунок линии выполняется слева направо или справа налево – нарисована горизонтальная линия. Нарисовать на листе можно что угодно: вертикальные лини (сверху вниз или снизу вверх), диагональ, любой рисунок. При этом лист расположен всё равно горизонтально. Чему? Столу. Полу. Нижнему этажу дома. Земле.
Если лист бумаги лежит на столе – лист расположен горизонтально. Рисунок линии выполняется слева направо или справа налево – нарисована горизонтальная линия. Нарисовать на листе можно что угодно: вертикальные лини (сверху вниз или снизу вверх), диагональ, любой рисунок. При этом лист расположен всё равно горизонтально. Чему? Столу. Полу. Нижнему этажу дома. Земле.
Горизонталь – самая знакомая из всех, базовая линия. Она в каких угодно смыслах служит основой любой композиции. Даже её визуальная тяжесть напоминает о том, что горизонтальная поверхность есть фундаментальная держащая основа. Она параллельна земле. Не зря изображение горизонтальной линии выражает вес, спокойствие, мир и стабильность.
Горизонтальность, как психологическое понятие
Горизонтальность линий в рисунках можно рассматривать через знание психологии. Прямые линии подразумевают некую разделительную черту. Человек, как зритель, может оставаться снаружи, заглядывая за неё, или перешагнуть этот горизонт, так сказать «переступить за черту». Прямые и чёткие линии выражают смелость и настойчивость, тонкие и изгибающиеся горизонтали – деликатность и мягкость.
Прямые и чёткие линии выражают смелость и настойчивость, тонкие и изгибающиеся горизонтали – деликатность и мягкость.
Горизонталь – топографическое определение
Самое простое определение этому слову можно найти в многочисленных словарях и энциклопедиях разных направлений. Чаще всего такое название применяется в отношении изогипс, т. е., линий, соединяющих точки, находящиеся на одинаковой абсолютной высоте над уровнем моря или любой другой взятой за основу плоскости.
Вот как расшифровывает это понятие Энциклопедический толковый словарь И.А. Ефрона и Ф.А. Брокгауза:
- Горизонтали – (изогипсы) линии, соединяющие на местности точки, лежащие на одной и той же высоте над уровнем моря или какой-то основной плоскости, принятой за основание.
Вот что можно прочитать в Техническом железнодорожном словаре:
- Горизонтали – линии на карте или плане местности, полученные от пересечения земной поверхности горизонтальными плоскостями, стоящими друг от друга на одинаковом расстоянии.

Выдержка из Геологической энциклопедии:
- Горизонтали – это линии, соединяющие точки одной высоты над уровнем моря. С помощью горизонталей на топографических картах отображаются особенности рельефа различных участков земной коры.
И в конце приведём текст определения из Справочника технического переводчика (отрасль машиностроение):
- Горизонтали – линии на поверхности, параллельные горизонтальной плоскости проекций.
Определение в профессиональном росте
У профессионалов есть такое понятие, как вектор карьеры. Многочисленные и очень сейчас популярные тренинги по достижению результатов в профессиональной деятельности и продвижении по лестнице к успешной карьере, выносят на обсуждение идеи, которые подразумевают рост потенциала человека как по вертикали, так и по горизонтали. По вертикали понятно, перешагивая ступени одну за другой, т. е., двигаясь вверх, индивид поднимается по вертикали. А что со вторым вариантом?
Здесь надо вспомнить шутливый принцип канадского педагога Питера Лоуренса, говорящий о том, что при подъёме по вертикали есть предел, та ступень, выше которой человек подняться не в состоянии. Ну что ж, доля правды в этом есть. Но, мало кто согласен остановиться на том, в чём он хорош. Значит, есть смысл продолжить рост в другом направлении.
Ну что ж, доля правды в этом есть. Но, мало кто согласен остановиться на том, в чём он хорош. Значит, есть смысл продолжить рост в другом направлении.
Рост по горизонтали означает углубление специалиста в экспертную область. Индивид становится отличным мастером и непревзойдённым экспертом в конкретном виде деятельности, конкретном направлении. Он делает свою работу, у него те же обязанности, но при этом освоены и применяются новые инструменты к выполнению возложенных задач. С некоторым временем его работа становится качественнее и выполняется виртуознее, за что профессионал больше ценится начальством и внешними партнёрами.
Другой вариант развития профессиональной деятельности по горизонтали – это переход в параллельное направление, приобретение в нём новых навыков, в том числе и во многих других областях. Это необходимо, когда в компании практикуют перестановку сотрудников из одного блока в другой. Например, из финансового отдела в логистику. С одной стороны, специалист вносит в это новое подразделение знания из других областей, с другой – учится всё время новому. Сотрудник сильно развивается личностно, что непременно скажется на его профессиональных качествах.
Сотрудник сильно развивается личностно, что непременно скажется на его профессиональных качествах.
Многие профессионалы вполне остаются довольны ростом по горизонтали и не нуждаются в росте по вертикали, мотивируя это таким немаловажным бонусом, как меньшая ответственность. Самое главное, что в этом случае человек должен понять, в какой своей роли он будет наиболее успешен, ценен для профессии и эффективен для результата. Здесь надо хорошо продумать свои шаги по карьерной лестнице и быть честным с собой самим. Тем более что не все хотят быть руководителями.
горизонтальных и вертикальных линий | Purplemath
Наклон и формулаПар. & Перп. Lines
Purplemath
Давайте снова рассмотрим два уравнения, которые мы сделали сначала на предыдущей странице, и сравним уравнения линий с их значениями наклона.
Уравнение первой линии было
Y = ( 2 / 3 ) x — 4, а наклон линии составлял M = 2 / 3 .
Уравнение второй линии было y = −2 x + 3, а наклон линии был равен м = −2.
В обоих случаях число, умноженное на переменную x , также было значением наклона этой линии. Это соотношение всегда выполняется: если уравнение прямой имеет вид « y =», то число, умноженное на x , является значением уклона м .
Содержание продолжается ниже
MathHelp.com
Это соотношение станет очень важным, когда вы начнете работать с уравнениями прямых.
Теперь давайте рассмотрим эти два уравнения и их графиков .
Для первого уравнения
y = ( 2 / 3 ) x − 4, уклон составил м = 2 9001 6 / 3 положительное число. График выглядел так:
Обратите внимание, как линия, когда мы двигаемся слева направо по оси x , поднимается вверх к верхней части рисунка; технически линия представляет собой «возрастающую» линию. И… наклон был положительным.
И… наклон был положительным.
Это соотношение всегда верно: если линия возрастает, то ее наклон будет положительным; а если наклон линии положительный, то ее график будет возрастающим.
Для второй строки y = −2 x + 3, наклон м = -2, отрицательное число. График выглядел следующим образом:
Обратите внимание, как линия, когда мы двигаемся слева направо вдоль оси x , опускается вниз к нижней части рисунка; технически линия представляет собой «убывающую» линию. И… склон был отрицательным.
Это соотношение всегда верно: если линия убывает, то ее наклон будет отрицательным; а если наклон линии отрицателен, то ее график будет убывающим.
Эта связь между знаком на наклоне и направлением графика линии может помочь вам проверить ваши расчеты: если вы вычисляете наклон как отрицательное, но вы можете видеть из графика уравнения, что линия на самом деле увеличивается (поэтому наклон должен быть положительным), тогда вы знаете, что вам нужно переделать свои расчеты. Знание об этой связи может сэкономить вам баллы на тесте, потому что это позволит вам проверить свою работу перед , вы сдаете его.
Знание об этой связи может сэкономить вам баллы на тесте, потому что это позволит вам проверить свою работу перед , вы сдаете его.
Итак, теперь мы знаем: возрастающие линии имеют положительный наклон, а убывающие линии имеют отрицательный наклон. Имея это в виду, рассмотрим следующую горизонтальную линию:
y = 4
Ее график показан ниже:
Горизонтальная линия направлена вверх; то есть это возрастающая линия? Нет, поэтому его наклон не может быть положительным. Горизонтальная линия направлена вниз; то есть это убывающая линия? Нет, поэтому его наклон не может быть отрицательным. Какое число не является ни положительным, ни отрицательным?
Ноль!
Таким образом, наклон этой (и любой другой) горизонтальной линии логически должен быть равен нулю. Проведем расчеты, чтобы убедиться в этом. Используя (произвольные) точки на линии (−3, 4) и (5, 4), наклон вычисляется как:
Это соотношение всегда сохраняется: нулевой наклон означает, что линия горизонтальна, а горизонтальная линия означает, что вы получите нулевой наклон.
(Кстати, все горизонтальные линии имеют вид « y = некоторое число», а уравнение « y = некоторое число» всегда отображается в виде горизонтальной линии.)
Теперь рассмотрим следующую вертикальную линию:
x = 4
График показан ниже .
Вертикальная линия идет вверх с одного конца? Ну да, вроде. Так что, может быть, наклон будет положительным…? Вертикальная линия идет вниз с другого конца? Ну, опять вроде как Так что, возможно, наклон будет отрицательным…?0011 оба положительные и отрицательные? Неа.
Вердикт: вертикальные линии НЕТ НАКЛОНА. Концепция наклона просто не работает для вертикальных линий. Наклон вертикальной линии не существует , а не !
Давайте проведем расчеты, чтобы подтвердить логику. Из графика линии я буду использовать (произвольно) точки (4, 5) и (4, −3). Тогда наклон равен:
Мы не можем делить на ноль, поэтому, конечно, это значение наклона «не определено».
Это соотношение верно всегда: вертикальная линия не имеет наклона, а «наклон не определен» или «линия не имеет наклона» означает, что линия вертикальна.
(Кстати, все вертикальные линии имеют форму « x = некоторое число», а « x = некоторое число» означает, что линия вертикальна. Каждый раз, когда ваша линия включает неопределенный наклон, линия вертикальной; и каждый раз, когда линия вертикальная, вы закончите делением на ноль, если попытаетесь вычислить наклон.)
Предупреждение: очень часто путают эти два типа линий и их наклоны, но они очень разные.
Как «горизонтальный» совсем не то же самое, что «вертикальный», так и «нулевой наклон» совсем не то же самое, что «без наклона».
Точно так же, как «Z» (с двумя горизонтальными линиями) не то же самое, что «N» (с двумя вертикальными линиями), так и «Нулевой» наклон (для горизонтальной линии) не то же самое, что » Нет» наклона (для вертикальной линии).
Число «ноль» существует, поэтому горизонтальные линии действительно имеют наклон. Но вертикальные линии не имеют наклона; «наклон» просто не имеет никакого значения для вертикальных линий.
Но вертикальные линии не имеют наклона; «наклон» просто не имеет никакого значения для вертикальных линий.
Очень часто тесты содержат вопросы, касающиеся горизонталей и вертикалей. Не путайте их!
URL: https://www.purplemath.com/modules/slope2.htm
Страница 1 Страница 3
Горизонтальные и вертикальные линии и прямоугольники в Python
питон > Основы > Горизонтальные и вертикальные линии и прямоугольники
Предложить редактирование этой страницыКак добавить аннотированные горизонтальные и вертикальные линии в Python.
Впервые в сюжете?
Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.
Горизонтальные и вертикальные линии и прямоугольники¶
введен в сюжет 4.12
Горизонтальные и вертикальные линии и прямоугольники, охватывающие всю
сюжет можно добавить через add_hline , add_vline , add_hrect и add_vrect методы plotly.graph_objects.Рисунок . Фигуры, добавленные с помощью этих методов,
добавлены в виде форм макета (как показано при выполнении print(fig) , для
пример). Эти формы привязаны к конечным точкам одной оси, независимо от
диапазон графика и привязан к координатам данных на другой оси.
ниже показаны некоторые возможности, попробуйте панорамировать и масштабировать получившуюся фигуру
чтобы увидеть, как фигуры прилипают к некоторым осям:
В [1]:
импортировать plotly.express как px df = px.data.iris() рис = px.scatter(df, x="petal_length", y="petal_width") fig.add_hline(y=0,9) fig.add_vrect(x0=0.9, x1=2) рис.шоу()
Эти фигуры можно стилизовать, передав те же аргументы, что и add_shape :
В [2]:
импортировать plotly.express как px df = px.data.iris() рис = px.scatter(df, x="petal_length", y="petal_width") fig.add_vline(x=2.5, line_width=3, line_dash="тире", line_color="зеленый") fig.add_hrect(y0=0,9, y1=2,6, line_width=0, fillcolor="красный", непрозрачность=0,2) рис.шоу()
Горизонтальные и вертикальные линии в Dash¶
Dash — лучший способ создавать аналитические приложения на Python с использованием рисунков Plotly. Чтобы запустить приложение ниже, запустите pip install dash , нажмите «Загрузить», чтобы получить код, и запустите python app.py .
Начните с официальной документации Dash, а узнайте, как с легкостью создавать и развертывать подобные приложения с помощью Dash Enterprise.
Выход[3]:
Добавление текстовых аннотаций¶
Текстовые аннотации могут быть дополнительно добавлены к автофигуре
с использованием аргумента ключевого слова annotation_text и позиционирования с использованием аргумента annotation_position :
В [4]:
импортировать plotly.express как px df = px.data.stocks(indexed=True) рис = px.line (df) fig.add_hline(y=1, line_dash="точка", annotation_text="1 января 2018 г. – базовый уровень", annotation_position="внизу справа") fig.add_vrect(x0="2018-09-24", x1="2018-12-18", annotation_text="отклонение", annotation_position="вверху слева", fillcolor="зеленый", непрозрачность=0,25, line_width=0) рис.шоу()
Дополнительное форматирование аннотации можно выполнить с помощью магических подчеркиваний с префиксом annotation_ или путем передачи экземпляра dict или go.layout.Annotation в аргумент аннотации :
В [5]:
импортировать plotly.express как px
df = px.data.stocks(indexed=True)
рис = px.line (df)
fig.add_hline(y=1, line_dash="точка",
annotation_text="1 января 2018 г. – базовый уровень",
annotation_position="внизу справа",
annotation_font_size=20,
annotation_font_color="синий"
)
fig. add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
аннотация = dict (font_size = 20, font_family = "Times New Roman"),
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
аннотация = dict (font_size = 20, font_family = "Times New Roman"),
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
Добавление к нескольким аспектам/подграфикам¶
Одну и ту же строку или блок можно добавить к нескольким подграфикам или аспектам, установив для строки и/или столбца значение «все» . По умолчанию ряд и столбец значения "все" .
В [6]:
импортируйте plotly.express как px.
df = px.data.stocks(indexed=True)
рис = px.line(df, facet_col="company", facet_col_wrap=2)
fig.add_hline(y=1, line_dash="точка", row=3, col="все",
annotation_text="1 января 2018 г. – базовый уровень",
annotation_position="внизу справа")
fig.add_vrect(x0="2018-09-24", x1="2018-12-18", row="all", col=1,
annotation_text="отклонение", annotation_position="вверху слева",
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис. шоу()
шоу()
Справочник¶
Доступны дополнительные сведения о формах макета и аннотациях.
Справочная документация также доступна для add_hline , add_vline , add_hrect , add_vrect .
А как насчет Dash?¶
Dash — это платформа с открытым исходным кодом для создания аналитических приложений, не требующая Javascript и тесно интегрированная с графической библиотекой Plotly.
Узнайте, как установить Dash, по адресу https://dash.plot.ly/installation.
Везде на этой странице, где вы видите fig.show() , вы можете отобразить один и тот же рисунок в приложении Dash, передав его аргументу figure компонента Graph из встроенного dash_core_components пакет вроде этого:
import plotly.graph_objects как go # или plotly.express как px fig = go.Figure() # или любая функция Plotly Express, например. px.bar(...) # fig.add_trace( ... ) # fig.update_layout( ... ) импортировать тире импортировать dash_core_components как DCC импортировать dash_html_components как html приложение = тире.Dash() app.layout = html.Div([ dcc.Graph(рисунок=рис) ]) app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter
ORCCA Горизонтальные, вертикальные, параллельные и перпендикулярные линии
Горизонтальные и вертикальные линии имеют некоторые особенности, заслуживающие нашего внимания. Кроме того, если пара прямых параллельна или перпендикулярна друг другу, мы можем сказать о них кое-что интересное. В этом разделе рассматриваются эти геометрические особенности, которые могут иметь линии.
Рисунок 4.8.1. Горизонтальная линия Рисунок 4.8.2. Вертикальная линия Рисунок 4.8.3. Параллельные линии Рисунок 4.8.4. Перпендикулярные линииПодраздел 4.8.1 Горизонтальные линии и вертикальные линии
В разделе 4.7 мы узнали, что все строки можно записать в стандартной форме. Когда \(A\) или \(B\) равно \(0\text{,}\), мы получаем горизонтальную или вертикальную линию, как мы скоро увидим. Давайте возьмем линейное уравнение стандартной формы, пусть \(A=0\) и \(B=0\) по одному, и упростим каждое уравнение.
Когда \(A\) или \(B\) равно \(0\text{,}\), мы получаем горизонтальную или вертикальную линию, как мы скоро увидим. Давайте возьмем линейное уравнение стандартной формы, пусть \(A=0\) и \(B=0\) по одному, и упростим каждое уравнение.
\начать{выровнять*} Ax+By\amp=C\amp Ax+By\amp=C\\ \substitute{0}x+By\amp=C\amp Ax+\substitute{0}y\amp=C\\ By\amp=C\amp Ax\amp=C\\ y\amp=\divideunder{C}{B}\amp x\amp=\divideunder{C}{A}\\ y\amp=k\amp x\amp=h \end{выравнивание*}
В конце мы просто переименовали постоянные числа \(\frac{C}{B}\) и \(\frac{C}{A}\) в \(k\) и \(h\) по традиции . Важно то, что вы просматриваете \(h\) и \(k\) (а также \(A\text{,}\) \(B\text{,}\) и \(C\)) как константы: числа, которые имеют определенное значение и не меняются в контексте одной задачи.
Подумайте хотя бы об одном из этих последних уравнений: \(y=k\text{.}\) Оно говорит, что значение \(y\) одинаково независимо от того, где вы находитесь на линии. Если вы хотите нанести точки на эту линию, вы можете двигаться далеко влево или далеко вправо по оси \(x\), но тогда вы всегда двигаетесь вверх (или вниз), чтобы сделать \(y \)-значение равно \(k\text{. }\) Как выглядит такая строка?
}\) Как выглядит такая строка?
Пример 4.8.5.
Построим линию с уравнением \(y=3\text{.}\) (Обратите внимание, что это то же самое, что и \(0x+1y=3\text{.}\))
Для построения точек не имеет значения, какие \(x\)-значения мы используем. Все, что имеет значение, это то, что \(y\) всегда \(3\text{.}\)
Такая линия горизонтальна , параллельна горизонтальной оси. Все строки с уравнением вида
\begin{equation*} у=к \end{equation*}
(или, в стандартной форме, \(0x+By=C\)) равно горизонтальный .
Рисунок 4.8.6. \(у=3\)Пример 4.8.7.
Давайте построим линию с уравнением \(x=5\text{.}\) (Обратите внимание, что это то же самое, что и \(1x+0y=5\text{.}\))
Линия имеет \(x=5\text{,}\), поэтому для построения точек нам требуется , чтобы перейти к \(x=5\text{.}\) Отсюда у нас есть полная свобода двигаться так далеко, как нам нравится вверх или вниз.
Такая линия вертикальна , параллельна вертикальной оси. Все строки с уравнением в форме
\begin{уравнение*} х=ч \end{equation*}
(или, в стандартной форме, \(Ax+0y=C\)) вертикальны.
Рисунок 4.8.8. \(х=5\)Пример 4.8.9. Нулевой наклон.
В контрольной точке 4.4.16 мы узнали, что наклон горизонтальной линии равен \(0\text{,}\) . Таким образом, числитель в формуле наклона равен \(0\text{.}\). Теперь, если мы знаем наклон линии и ее точку пересечения \(y\), мы можем использовать форму точки пересечения наклона, чтобы написать ее уравнение:
\начать{выровнять*} у\амп=мх+б\\ у\усилитель=0x+b\\ у\ампер=б \end{выравнивание*}
Это дает нам альтернативный способ думать об уравнениях горизонтальных линий. Они имеют некоторый \(y\)-перехват \((0,b)\) и имеют наклон \(0\text{.}\)
Мы используем горизонтальные линии для моделирования сценариев, в которых значения \(y\) не изменяются, например, когда Като остановился на \(12\) часов (он заслужил отдых)!
КПП 4.
 8.10. Точки построения.
8.10. Точки построения.Пример 4.8.11. Неопределенный наклон.
Каков наклон вертикальной линии? На рис. 4.8.12 показаны три линии, проходящие через начало координат, каждая из которых круче предыдущей. На каждом графике вы можете видеть треугольник наклона, который каждый раз использует «подъем» \(4\).
Рисунок 4.8.12.Если бы мы продолжали делать линию все круче и круче, пока она не стала вертикальной, треугольник наклона по-прежнему имел бы «подъем» в \(4\text{,}\), но «пробег» становился бы все меньше и меньше, приближаясь к \ (0\text{.}\) И тогда наклон будет \(m=\frac{4}{\text{очень маленький}}=\text{очень большой}\text{.}\) Таким образом, наклон вертикальную линию можно рассматривать как «бесконечно большую».
Если мы на самом деле попытаемся вычислить уклон, используя треугольник наклона, когда пробег равен \(0\text{,}\), мы получим \(\frac{4}{0}\text{,}\), который не определен . Поэтому мы также говорим, что наклон вертикальной линии равен не определено . Некоторые люди говорят, что вертикальная линия не имеет наклона.
Некоторые люди говорят, что вертикальная линия не имеет наклона.
КПП 4.8.14. Точки построения.
Пример 4.8.15.
Пусть \(x\) представляет собой цену нового \(60\)-дюймового телевизора в Target в Черную пятницу (которая составляла \(\$650\)), а \(y\) — количество часов, в течение которых вы будет смотреть что-то на этом телевизоре за всю его жизнь. Какая связь между \(x\) и \(y\text{?}\)
Что ж, нельзя обойти стороной тот факт, что \(x=650\text{.}\) Что касается \(y\text{,}\) без дополнительной информации о ваших привычках просмотра, то теоретически оно может быть столь же низким как \(0\) или может быть больше. Если мы нарисуем этот сценарий, мы должны изобразить уравнение \(x=650\text{,}\), которое, как мы теперь знаем, дает вертикальную линию, и мы получим рисунок 4.8.16.
Рисунок 4.8.16. Новый телевизор: количество часов просмотра по сравнению с ценой покупки; отрицательные \(y\)-значения опущены, поскольку они не имеют смысла в контекстеКраткое изложение уравнений горизонтальной и вертикальной линий.
| Горизонтальные линии | Вертикальные линии |
Линия горизонтальна тогда и только тогда, когда ее уравнение может быть записано \begin{уравнение*} у=к \end{уравнение*} для некоторой константы \(k\text{.}\) | Строка вертикальный тогда и только тогда, когда его уравнение может быть записано \begin{уравнение*} х=ч \end{уравнение*} для некоторой константы \(h\text{.}\) |
В стандартной форме любая строка с уравнением \begin{уравнение*} 0x+By=С \end{уравнение*} горизонтальный. | В стандартной форме любая строка с уравнением \begin{уравнение*} Ах+0у=С \end{уравнение*} вертикальный. |
Если линия с уравнением \(y=k\) горизонтальна, она имеет точку пересечения \(y\) в точке \((0,k)\) и наклон \(0\text{.} \) | Если линия с уравнением \(x=h\) вертикальна, она имеет точку пересечения \(x\) в точке \((h,0)\) и ее наклон равен undefined . Некоторые говорят, что у него нет наклона , а некоторые говорят, что наклон бесконечно большой . |
В форме пересечения наклона любая линия с уравнением \begin{уравнение*} у=0х+б \end{уравнение*} горизонтальный. | Невозможно записать уравнение вертикальной линии в форме наклон-отрезок, потому что вертикальные линии не имеют определенного наклона. |
Подраздел 4.8.2 Параллельные линии
Пример 4.8.17.
Два дерева были посажены в один и тот же год, и их рост с течением времени моделируется двумя линиями на рисунке 4. 8.18. Используйте линейные уравнения для моделирования роста каждого дерева и интерпретируйте их значения в этом контексте.
8.18. Используйте линейные уравнения для моделирования роста каждого дерева и интерпретируйте их значения в этом контексте.
Мы видим, что уравнение Дерева 1 имеет вид \(y=\frac{2}{3}x+2\text{,}\), а уравнение Дерева 2 имеет вид \(y=\frac{2}{3}x+5 \text{.}\) Дерево 1 было \(2\) футов высотой, когда оно было посажено, а Дерево 2 было \(5\) футов высотой, когда оно было посажено. Оба дерева растут с одинаковой скоростью, \(\frac{2}{3}\) футов в год или \(2\) футов каждые \(3\) лет.
Сейчас важно отметить, что эти две линии параллельны. Почему? Для линий с положительным наклоном чем больше наклон линии, тем круче наклон линии. В результате, если две линии имеют одинаковый наклон, они наклонены под одним и тем же углом, следовательно, они параллельны.
Факт 4.8.19.
Любые две вертикальные линии параллельны друг другу. Две невертикальные прямые параллельны тогда и только тогда, когда они имеют одинаковый наклон.
КПП 4.8.20.
КПП 4.8.21.
Подраздел 4.8.3 Перпендикулярные линии
Наклоны двух перпендикулярных линий также имеют особое отношение.
На рис. 4.8.22 показано объяснение этой связи.
(a) Две общие перпендикулярные линии, одна из которых имеет наклон \(m\text{.}\)(b) Поскольку один наклон равен \(m\text{,}\), мы можем нарисовать треугольник наклона с помощью «run» \(1\) и «подниматься» \(m\text{.}\)(c) A конгруэнтный треугольник наклона можно нарисовать для перпендикулярной линии. Его ноги имеют одинаковую длину, но в разных положениях, и одна из них отрицательная. Рисунок 4.8.22. Соотношение между наклонами перпендикулярных линий. Вторая линия на рисунке 4.8.22 имеет наклон
.\begin{уравнение*} \frac{\Delta y}{\Delta x}=\frac{-1}{m}=-\frac{1}{m}\text{.} \end{уравнение*}
Факт 4.8.23.
Вертикальная линия и горизонтальная линия перпендикулярны. Для линий, которые не являются ни вертикальными, ни горизонтальными, они перпендикулярны тогда и только тогда, когда наклон одной является отрицательной обратной величиной наклона другой. То есть, если у одного есть наклон \(m\text{,}\), у другого есть наклон \(-\frac{1}{m}\text{.}\)
То есть, если у одного есть наклон \(m\text{,}\), у другого есть наклон \(-\frac{1}{m}\text{.}\)
Другой способ сказать это так: произведение наклонов двух перпендикулярных линий равно \(-1\) (предполагая, что обе линии изначально имеют наклон).
Не убежден? Вот три пары перпендикулярных линий, по которым мы можем видеть, сохраняется ли шаблон.
Рисунок 4.8.24. Графики \(y=2x-2\) и \(y=-\frac{1}{2}x+2\text{.}\) Обратите внимание на соотношение между их наклонами: \(2=-\frac{1 }{-\sfrac{1}{2}}\)Рисунок 4.8.25. Графики \(y=-3x+4\) и \(y=\frac{1}{3}x-3\text{.}\) Обратите внимание на соотношение между их наклонами: \(-3=-\frac{ 1}{\sfrac{1}{3}}\)Рисунок 4.8.26. Графики \(y=x\) и \(y=-x\text{.}\) Обратите внимание на соотношение между их наклонами: \(1=-\frac{1}{-1}\)Пример 4.8.27.
Линия \(A\) проходит через \((-2,10)\) и \((3,-10)\text{.}\) Линия \(B\) проходит через \((-4,- 4)\) и \((8,-1)\text{.}\) Определите, являются ли эти две прямые параллельными, перпендикулярными или ни тем, ни другим.
Объяснение
Мы будем использовать формулу наклона, чтобы найти наклоны обеих линий:
\begin{align*} \text{Линия }A\text{наклон}\amp=\frac{y_2-y_1}{x_2-x_1}\amp\text{Линия }B\text{наклон}\amp=\frac{y_2 -y_1}{x_2-x_1}\\ \amp=\frac{-10-10}{3-(-2)}\amp\amp=\frac{-1-(-4)}{8-(-4)}\\ \amp=\frac{-20}{5}\amp\amp=\frac{3}{12}\\ \amp=-4\amp\amp=\frac{1}{4} \end{выравнивание*}
Их наклоны неодинаковы, поэтому эти две линии не параллельны.
Произведение их наклонов равно \((-4)\cdot\frac{1}{4}=-1\text{,}\text{,}\), что означает, что две линии перпендикулярны.
КПП 4.8.28.
Упражнения 4.8.4 Упражнения
Обзор и прогрев
1.
Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).
\(\displaystyle{ \frac{0}{2} = }\)
\(\displaystyle{ \frac{2}{0} = }\)
2.

Оцените следующие выражения. Если ответ не определен, вы можете указать DNE (что означает «не существует»).
\(\displaystyle{ \frac{3}{0} = }\)
\(\displaystyle{ \frac{0}{3} = }\)
3.
Прямая проходит через точки \((4,-4)\) и \((-5,-4)\text{.}\) Найдите наклон этой линии.
4.
Прямая проходит через точки \((2,-1)\) и \((-3,-1)\text{.}\) Найдите наклон этой линии.
5.
Прямая проходит через точки \((1,-1)\) и \((1,5)\text{.}\) Найдите наклон этой линии.
6.
Прямая проходит через точки \((3,-3)\) и \((3,3)\text{.}\) Найдите наклон этой линии.
7.
Рассмотрим уравнение:
\begin{уравнение*} у=1 \end{уравнение*}
Какие из следующих упорядоченных пар являются решениями данного уравнения? Может быть более одного правильного ответа.
\(\displaystyle (1,3)\)
\(\displaystyle (-9,1)\)
\(\displaystyle (8,1)\)
\(\displaystyle (0,10)\)
8.
Рассмотрим уравнение:
\begin{уравнение*} у=1 \end{уравнение*}
Какие из следующих упорядоченных пар являются решениями данного уравнения? Может быть более одного правильного ответа.
\(\displaystyle (-2,1)\)
\(\displaystyle (1,6)\)
\(\displaystyle (9,1)\)
\(\displaystyle (0,7)\)
9.
Рассмотрим уравнение:
\begin{уравнение*} х+1=0 \end{уравнение*}
Какие из следующих упорядоченных пар являются решениями данного уравнения? Может быть более одного правильного ответа.
\(\displaystyle (1,-1)\)
\(\displaystyle (0,-7)\)
\(\displaystyle (-1,0)\)
\(\displaystyle (-1,5)\)
10.
Рассмотрим уравнение:
\begin{уравнение*} х+1=0 \end{уравнение*}
Какие из следующих упорядоченных пар являются решениями данного уравнения? Может быть более одного правильного ответа.
\(\displaystyle (-1,1)\)
\(\displaystyle (-1,0)\)
\(\displaystyle (0,-9)\)
\(\displaystyle (1,-1)\)
Столы для горизонтальных и вертикальных линий
11.
Заполните эту таблицу для уравнения \(y=3\text{.}\) Первая строка является примером.
| \(х\) | \(у\) | Очки |
| \(-3\) | \(3\) | \(\влево(-3,3\вправо)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
12.
Заполните эту таблицу для уравнения \(y=4\text{. }\) Первая строка является примером.
}\) Первая строка является примером.
| \(х\) | \(у\) | Очки |
| \(-3\) | \(4\) | \(\влево(-3,4\вправо)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
13.
Заполните эту таблицу для уравнения \(x=-6\text{.}\) Первая строка является примером.
| \(х\) | \(у\) | Очки |
| \(-6\) | \(-3\) | \(\влево(-6,-3\вправо)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
14.
Заполните эту таблицу для уравнения \(x=-5\text{.}\) Первая строка является примером.
| \(х\) | \(у\) | Очки |
| \(-5\) | \(-3\) | \(\влево(-5,-3\вправо)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
Линейные уравнения
15.
Прямая проходит через точки \((-1,3)\) и \((-4,3)\text{.}\) Найдите уравнение для этой прямой.
16.
Прямая проходит через точки \((-4,6)\) и \((1,6)\text{.}\) Найдите уравнение для этой прямой.
17.
Прямая проходит через точки \((8,3)\) и \((8,5)\text{. }\) Найдите уравнение для этой прямой.
}\) Найдите уравнение для этой прямой.
18.
Прямая проходит через точки \((10,-1)\) и \((10,-4)\text{.}\) Найдите уравнение для этой прямой.
19.
Показан линейный график. Напишите уравнение прямой.
20.
Показан линейный график. Напишите уравнение прямой.
21.
Показан линейный график. Напишите уравнение прямой.
22.
Показан линейный график. Напишите уравнение прямой.
Перехваты
23.
Найдите точку пересечения \(y\) и точку пересечения \(x\) прямой, заданной уравнением. Если определенного перехвата не существует, введите нет во все поля для ответов в этой строке.
\begin{уравнение*} х = 1 \end{уравнение*}
| \(х\)-значение | \(y\)-значение | Местоположение | |
| \(y\)-перехват | |||
| \(х\)-перехват |
24.

Найдите точку пересечения \(y\) и точку пересечения \(x\) прямой, заданной уравнением. Если определенного перехвата не существует, введите нет во все поля для ответов в этой строке.
\begin{уравнение*} х = 3 \end{уравнение*}
| \(х\)-значение | \(y\)-значение | Местоположение | |
| \(y\)-перехват | |||
| \(х\)-перехват |
25.
Найдите точку пересечения \(y\) и точку пересечения \(x\) прямой, заданной уравнением. Если определенного перехвата не существует, введите нет во все поля для ответов в этой строке.
\begin{уравнение*} у = 5 \end{уравнение*}
| \(х\)-значение | \(y\)-значение | Местоположение | |
| \(y\)-перехват | |||
| \(х\)-перехват |
26.

Найдите точку пересечения \(y\) и точку пересечения \(x\) прямой, заданной уравнением. Если определенного перехвата не существует, введите нет во все поля для ответов в этой строке.
\begin{уравнение*} у = 8 \end{уравнение*}
| \(х\)-значение | \(y\)-значение | Местоположение | |
| \(y\)-перехват | |||
| \(х\)-перехват |
Графики горизонтальных и вертикальных линий
27.
Нарисуйте линию \(y=1\text{.}\)
28.
Нарисуйте линию \(y+5=0\text{.}\)
29.
Нарисуйте линию \(y-6=0\text{.}\)
30.
Нарисуйте линию \(x=2\text{.}\)
31.
Нарисуйте линию \(x+4=0\text{.}\)
32.
Нарисуйте линию \(x-3=0\text{.}\)
Параллельно или перпендикулярно?
33.

Линия \(m\) проходит через точки \((-4,-25)\) и \((1,0)\text{.}\)
Линия \(n\) проходит через точки \((1,-4)\) и \((5,16)\text{.}\)
Эти две строки
.34.
Линия \(m\) проходит через точки \((-9,4)\) и \((-27,8)\text{.}\)
Линия \(n\) проходит через точки \((9,-11)\) и \((-18,-5)\text{.}\)
Эти две строки равны
.35.
Линия \(m\) проходит через точки \((6,-1)\) и \((-6,5)\text{.}\)
Линия \(n\) проходит через точки \((1,-8)\) и \((2,-6)\text{.}\)
Эти две строки
.36.
Линия \(m\) проходит через точки \((6,-10)\) и \((-9,10)\text{.}\)
Линия \(n\) проходит через точки \((8,-3)\) и \((-8,-15)\text{.}\)
Эти две строки равны
.37.
Линия \(m\) проходит через точки \((4,-4)\) и \((-5,23)\text{.}\)
Линия \(n\) проходит через точки \((1,10)\) и \((-3,-2)\text{.}\)
Эти две строки
.38.
Линия \(m\) проходит через точки \((1,1)\) и \((-5,1)\text{. }\)
}\)
Линия \(n\) проходит через точки \((10,-5)\) и \((-9,-5)\text{.}\)
Эти две строки
.39.
Линия \(m\) проходит через точки \((3,-6)\) и \((3,3)\text{.}\)
Линия \(n\) проходит через точки \((10,10)\) и \((10,1)\text{.}\)
Эти две строки
.40.
Линия \(m\) проходит через точки \((5,7)\) и \((5,-9)\text{.}\)
Линия \(n\) проходит через точки \((4,10)\) и \((4,-10)\text{.}\)
Эти две строки
.Уравнения параллельных и перпендикулярных линий
41.
Прямая проходит через точку \((-2,0)\text{,}\) и параллельна прямой \(y=8\text{.}\) Найдите уравнение для этой прямой.
42.
Прямая проходит через точку \((9,-7)\text{,}\) и она параллельна прямой \(y=10\text{.}\) Найдите уравнение для этой прямой.
43.
Прямая проходит через точку \((6,-4)\text{,}\) и параллельна прямой \(x=-9\text{.}\) Найдите уравнение для этой прямой.
44.

Прямая проходит через точку \((-1,5)\text{,}\) и параллельна прямой \(x=-6\text{.}\) Найдите уравнение для этой прямой.
45.
Линия \(k\) и линия \(\ell\) параллельны.
Строка \(k\) имеет уравнение \(y=3x+3\text{.}\)
Линия \(\ell\) проходит через точку \((-5,-11)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
46.
Линия \(k\) и линия \(\ell\) параллельны.
Строка \(k\) имеет уравнение \(y=4x+5\text{.}\)
Линия \(\ell\) проходит через точку \((4,15)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
47.
Линия \(k\) и линия \(\ell\) параллельны.
Строка \(k\) имеет уравнение \(y=-\frac{1}{3}x+8\text{.}\)
Линия \(\ell\) проходит через точку \((-9,7)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Строка \(\ell\) в форме пересечения наклона равна
48.
Линия \(k\) и линия \(\ell\) параллельны.
Строка \(k\) имеет уравнение \(y=-\frac{2}{7}x-7\text{.}\)
Линия \(\ell\) проходит через точку \((14,1)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
49.
Линия \(k\) и линия \(\ell\) перпендикулярны.
Строка \(k\) имеет уравнение \(y=-x+5\text{.}\)
Линия \(\ell\) проходит через точку \((-3,1)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
50.
Линия \(k\) и линия \(\ell\) перпендикулярны.
Строка \(k\) имеет уравнение \(y=-3x-4\text{.}\)
Прямая \(\ell\) проходит через точку \(\left(2,-\frac{7}{3}\right)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
51.
Линия \(k\) и линия \(\ell\) перпендикулярны.
Строка \(k\) имеет уравнение \(y=\frac{5}{8}x+5\text{.}\)
Линия \(\ell\) проходит через точку \(\left(-2,\frac{36}{5}\right)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Линия \(\ell\) в форме пересечения наклона равна
52.

Линия \(k\) и линия \(\ell\) перпендикулярны.
Строка \(k\) имеет уравнение \(x-5y=-25\text{.}\)
Линия \(\ell\) проходит через точку \((3,-13)\text{.}\)
Найдите уравнение для линии \(\ell\) как в форме точки-наклона, так и в форме наклона-пересечения.
Линия \(\ell\) в форме точка-наклон равна
Строка \(\ell\) в форме пересечения наклона равна
Вызов
53.
Докажите, что треугольник с вершинами в точках \((1, 1)\text{,}\) \((-4, 4)\text{,}\) и \((-3, 0)\) является прямоугольным треугольником.
Как вставить горизонтальную или вертикальную линию в Microsoft Word
Линии являются важным элементом дизайна. В Microsoft Word горизонтальная или вертикальная линия может разделить документ и направить поток текста. Вы можете вставить строку в Word и отформатировать ее по-другому, чтобы превратить скромную строку во что-то более привлекательное.
Ведь это так просто. Но если вы не знаете всех способов сделать это, то этот учебник для начинающих о том, как вставить строку в Word, для вас.
Как вставить прямую линию в Word с помощью клавиатуры?
Знаете ли вы, что в Word можно быстро добавить строку, набрав несколько символов? Функция Word AutoFormat печатает данные для вас по мере их ввода. Возможно, вы уже видели его в действии, когда он создает автоматические маркированные списки.
Вы можете вставлять не только прямую линию, но и добавлять линии с различным дизайном. Вот как это работает:
- Поместите курсор в то место, где вы хотите начать горизонтальную линию.
- Затем введите три символа для любых возможных стилей линий, которые вы видите на снимке экрана ниже, — нажмите Введите . Например, чтобы нарисовать пунктирную линию, введите *** и нажмите Enter.
Как вы увидите, вы получите шесть вариантов стандартной горизонтальной линии.
- Простая одна строка с тремя дефисами (—)
- Ломаная или пунктирная линия с тремя звездочками (***)
- Простая двойная строка с тремя знаками равенства (===)
- Жирная одинарная строка с тремя символами подчеркивания (___)
- Тройная строка с жирным центром и тремя цифрами (###)
- Волнистая линия с тремя тильдами (~~~)
Строка занимает всю ширину страницы. При добавлении внутрь столбца строка вставляется в соответствии с шириной столбца. Если вы хотите добавить текст выше или ниже строки, поместите курсор в нужное место и начните печатать.
При добавлении внутрь столбца строка вставляется в соответствии с шириной столбца. Если вы хотите добавить текст выше или ниже строки, поместите курсор в нужное место и начните печатать.
Вы также заметите всплывающую крошечную кнопку «Параметры автозамены» рядом со строкой. Это ярлык, который позволяет вам отменить автоматическую строку, когда она вам не нужна, полностью остановить их или погрузиться в диалоговое окно параметров автоформата.
Вы можете навсегда отключить эти строки в диалоговом окне параметров автоформата.
Перейдите к Автоформат при вводе e вкладка > раздел Применить при вводе > снимите флажок Линии границ .
Вставка горизонтальной линии с ленты
Если вас раздражает автозамена и вы отключили этот параметр, есть еще один быстрый способ добавить горизонтальную линию.
1. Поместите курсор туда, куда вы хотите вставить строку.
2. Перейдите на вкладку Home и щелкните стрелку раскрывающегося списка для параметра Borders в группе Paragraph .
3. Выберите в меню Горизонтальная линия .
4. Чтобы настроить внешний вид этой горизонтальной линии, дважды щелкните ее. Диалоговое окно «Формат горизонтальной линии» позволяет изменить ширину, высоту, цвет и выравнивание линии.
5. Чтобы изменить размер линии, выберите линию двойным щелчком, а затем перетащите любую из точек изменения размера, чтобы изменить длину или ширину.
6. Чтобы удалить строку, выберите ее и нажмите Удалить на клавиатуре.
Использование границ для добавления горизонтальных и вертикальных линий
Параметр «Границы» в группе «Абзац» также дает вам другой способ вставить верхнюю или нижнюю границу, которая напоминает горизонтальную линию в документе.
1. Щелкните абзац текста, в котором должна появиться строка.
2. Добрался до Дом и группы Параграф . Нажмите на кнопку Граница . Нижняя граница обычно используется по умолчанию. Это помещает строку под выделенным текстом на странице или абзацем, если вы не выбрали текст.
Нижняя граница обычно используется по умолчанию. Это помещает строку под выделенным текстом на странице или абзацем, если вы не выбрали текст.
3. Для других параметров (, таких как вертикальная рамка r), вы можете щелкнуть крошечную стрелку раскрывающегося списка на кнопке «Границы», чтобы получить доступ к списку параметров.
4. Чтобы изменить внешний вид любой границы, нажмите «Границы» и «Шади». Затем используйте диалоговое окно для настройки стиля, цвета и ширины границы .
5. Удаление этой горизонтальной линии в документе Word может быть неочевидным, но достаточно простым.
Использование фигур для вставки горизонтальной или вертикальной линии в Word
Меню «Фигуры» содержит несколько параметров линий. Эти формы линий имеют одно важное отличие — вы можете рисовать их под разными углами. Затем, после того как вы нарисуете линию, вы можете настроить цвет и внешний вид, чтобы сделать декоративные горизонтальные или вертикальные линии даже в середине документа Word.
1. Поместите курсор туда, куда вы хотите вставить строку.
2. Перейдите к Вставка > группа Иллюстрации > стрелка раскрывающегося списка Фигуры .
3. В группе Линии выберите форму линии.
4. Нажмите и перетащите по документу с нажатой мышью до конечной точки. ( Совет: Удерживая нажатой клавишу Shift, вставьте прямую линию, горизонтальную или вертикальную)
5. Оставьте линию выбранной, чтобы настроить внешний вид линии с помощью 9Вкладка 0241 Формат формы на ленте.
6. Перейдите на вкладку Стили формы , измените цвет, используйте другой стиль линии или примените эффекты.
7. Вы также можете щелкнуть правой кнопкой мыши строку и выбрать Format Shape из контекстного меню, чтобы открыть дополнительные параметры для изменения внешнего вида.
Как добавить вертикальную линию и разделить текст на столбцы
Текст, организованный в столбцы, является основным методом компоновки. Например, вы можете разделить текстовые блоки на несколько столбцов и вставить между ними вертикальную линию.
Например, вы можете разделить текстовые блоки на несколько столбцов и вставить между ними вертикальную линию.
1. Выберите текст.
2. Перейдите к Лента > Макет > (группа Параметры страницы) Столбцы . Щелкните раскрывающийся список и выберите необходимое количество столбцов.
3. Текст теперь разбит на столбцы. Нажмите на любой столбец и перейдите к Layout > Columns > More Columns .
4. В диалоговом окне Столбцы установите флажок Строка между и нажмите OK.
Обратите внимание, что в этом диалоговом окне вы также можете изменить количество столбцов и расстояние между ними.
Как использовать вкладку Bar для вставки вертикальной линии
Позиции табуляции в Word помогают выравнивать строки и абзацы. Вкладка панели , с другой стороны, не устанавливает вкладку. Вместо этого. Он вставляет вертикальную линию и разграничивает абзац на столбцы.
1. Выберите абзац, в который вы хотите добавить вертикальную линию.
2. Перейдите на ленту > Главная . В группе Paragraph щелкните маленькую стрелку, чтобы открыть Paragraph Settings .
3. Нажмите кнопку Tabs в нижней части диалогового окна.
4. В поле Позиция табуляции введите положение, в котором должна отображаться вертикальная линия. Вы можете использовать линейку в верхней части экрана, чтобы измерить значение, которое нужно ввести.
5. Нажмите кнопку Bar в разделе Alignment . Нажмите Установите и OK .
Как видите, я установил значение «-0,2», чтобы оно отображалось слева от первого абзаца. Чтобы удалить вертикальную линию, удалите вкладку полосы.
Также: Хотите сделать пустые строки, где читатель может заполнить некоторую информацию? Вы можете использовать вкладки для быстрого создания пустых строк в формах Microsoft Word.
Как вставить графику для творческих линий в Word
Использование изображений для горизонтальных и вертикальных линий может быть творческим решением. Но используйте их с осторожностью и избегайте чрезмерного использования их в документе, поскольку растянутое или сжатое изображение может в конечном итоге вернуться на бумагу или экран.
Графику можно использовать как прямую линию по горизонтали и по вертикали. Вот как:
- Перейдите к Лента > Вставка > Изображение .
- Выберите один из источников изображения в раскрывающемся списке. Например, выберите Это устройство , чтобы загрузить линейное изображение, созданное в другой программе.
- На приведенном ниже снимке экрана показана иллюстрация из Стоковые изображения . Точки привязки вокруг изображения помогают сжимать и растягивать изображение до состояния, напоминающего прямую линию. Используйте манипулятор поворота, чтобы отразить графику по вертикальной линии.

Вы можете использовать эти псевдостроки в качестве разделителей или частей верхнего или нижнего колонтитула документа. Используйте панель инструментов Graphics Format на ленте, чтобы отформатировать эту иллюстрацию с помощью Graphics Fill , Graphics Outline и Graphics Effects .
Нарисуйте линию в документе Word
Горизонтальные линии более очевидны и привычны. Но добавление вертикальных линий в нужном месте может повысить визуальную привлекательность вашего контента. Линии — это не просто украшения… они могут привлечь ваше внимание к самой важной части документа, если использовать их с осторожностью.
Подумайте о линиях и используйте эти методы в следующий раз, когда сядете писать профессиональный отчет в Microsoft Word.
Узнайте о вертикальных и горизонтальных линиях
Определение вертикальных и горизонтальных линий
В математике, особенно в двумерной евклидовой или координатной геометрии, вертикальные линии — это линии, параллельные вертикальному направлению, а линии, перпендикулярные этим вертикальным линиям, называемые горизонтальными линиями, горизонтальные линии не пересекаются и не пересекаются по оси x-x-x-, а вертикальные линии также не пересекаются и не пересекаются по оси y-y-y- на декартовой плоскости.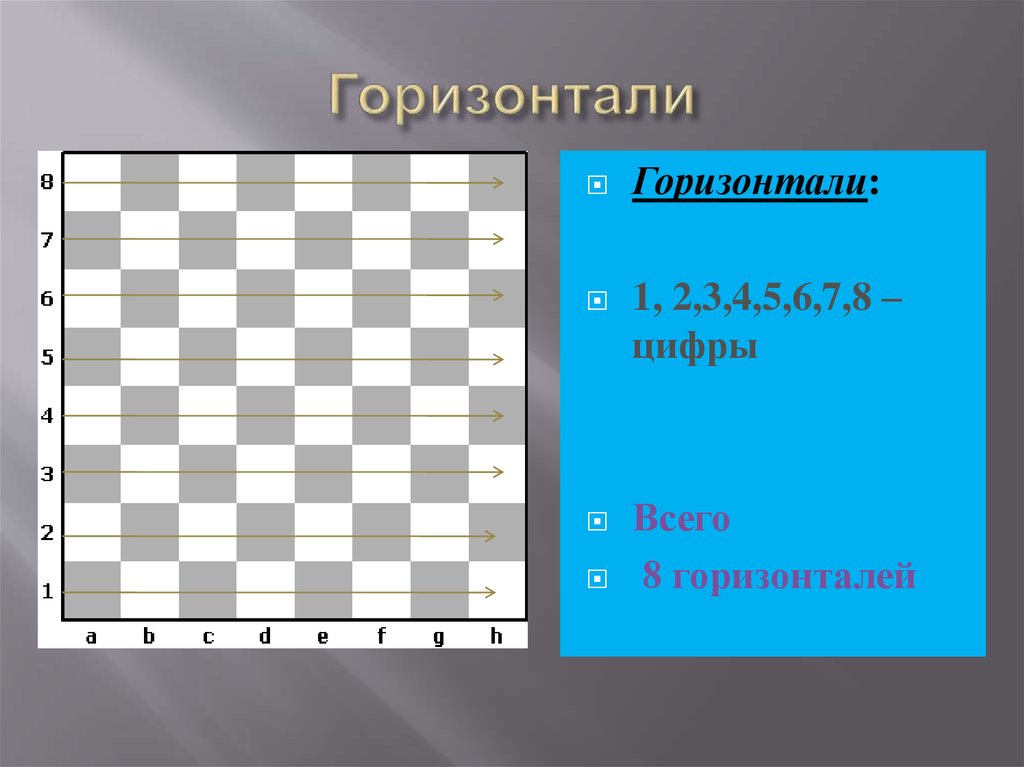
Обзор вертикальных и горизонтальных линий
Согласно истории математики, термин «горизонтальный» происходит от слова «горизонт». Принимая во внимание, что термин «вертикальный» берет свое начало от латинского слова «verticalis», что означает «высшая точка». В 1636 году французский математик и инженер Жирар Дезарг опубликовал книгу под названием «Перспектива», в которой он описывает вертикаль как перпендикулярную горизонту. В геофизических терминах, особенно в строительстве, технике и физике, термин «вертикаль» связан с объектами, которые идут вертикально вверх, а объекты, которые идут параллельно направлению горизонта слева направо, называются горизонтальными. Например, если стены на поверхности земли поднимаются или их высота увеличивается прямо вверх гораздо быстрее, чем их ширина, мы говорим, что они вертикальны, а если наоборот, мы говорим, что они горизонтальны. Эти стены могут либо пересекаться по вертикали, либо оставаться параллельными друг другу, поскольку горизонтальные поверхности не пересекаются и не пересекаются друг с другом. Но это верно только для сравнительно коротких расстояний, потому что теперь мы знаем, что Земля имеет шаровидную форму, а понятие горизонтали и вертикали не имеет значения. В целом общего определения вертикали и горизонтали не существует. Однако в двухмерной (2D) евклидовой или координатной геометрии можно решить любую из них, другая определяется автоматически. Например, если считать ось x-x-x- горизонтальной, то ось y-y-y- заведомо вертикальна или наоборот, что видно из следующего рисунка:
Но это верно только для сравнительно коротких расстояний, потому что теперь мы знаем, что Земля имеет шаровидную форму, а понятие горизонтали и вертикали не имеет значения. В целом общего определения вертикали и горизонтали не существует. Однако в двухмерной (2D) евклидовой или координатной геометрии можно решить любую из них, другая определяется автоматически. Например, если считать ось x-x-x- горизонтальной, то ось y-y-y- заведомо вертикальна или наоборот, что видно из следующего рисунка:
На приведенном выше рисунке также видно, что ось y-y-y-, расположенная горизонтально на столе, становится вертикальной на зеркале (или белой доске). Принимая во внимание, что горизонтальная линия, то есть ось x-x-x-, остается горизонтальной, что означает, что вертикаль связана с осью y-y-y-, а линии, параллельные ей, называются вертикальными линиями, тогда как линии, параллельные оси x Ось −xx− называются горизонтальными линиями в двумерной координатной геометрии. Однако понятие горизонтали и вертикали теряет смысл, как только мы входим в трехмерную (3D) геометрию.
Однако понятие горизонтали и вертикали теряет смысл, как только мы входим в трехмерную (3D) геометрию.
Есть вопрос по этой теме?
Что вы изучите:
- Определение вертикальных и горизонтальных линий
- Обзор вертикальных и горизонтальных линий
- Свойства горизонтальных и вертикальных линий в 2D
- Понимание горизонтальных и вертикальных линий с точки зрения координатной геометрии
- Работа с горизонтальными и вертикальными линиями
Свойства горизонтальных и вертикальных линий в 2D
Существуют определенные свойства, которые могут помочь вам идентифицировать горизонтальные и вертикальные линии на 2D декартовой плоскости в координатной геометрии. Они следующие:
Понимание горизонтальных и вертикальных линий с точки зрения координатной геометрии
Поскольку нам известно уравнение прямой линии на двумерной декартовой плоскости как y=mx+cy=mx+cy=mx+c, то если предположим, , либо наклон mmm, либо xxx остается нулевым, остается только y=cy=cy=c, где ccc — любое действительное число. Тогда семейство прямых y=cy=cy=c для всех ненулевых ccc есть не что иное, как горизонтальные прямые, и если yyy становится равным нулю, то для всех действительных m≠0m\ne 0m=0 и ccc x= −cm=ax=-\frac{c}{m}=ax=−mc=a, что есть не что иное, как совокупность всех вертикальных линий, где $a$ — другое действительное число. Для лучшего понимания обратите внимание на следующий рисунок:
Тогда семейство прямых y=cy=cy=c для всех ненулевых ccc есть не что иное, как горизонтальные прямые, и если yyy становится равным нулю, то для всех действительных m≠0m\ne 0m=0 и ccc x= −cm=ax=-\frac{c}{m}=ax=−mc=a, что есть не что иное, как совокупность всех вертикальных линий, где $a$ — другое действительное число. Для лучшего понимания обратите внимание на следующий рисунок:
Можно также проверить ранее упомянутые свойства по приведенному выше рисунку. На приведенном выше рисунке мы обозначили пересечение оси x-x-x- и оси y-y-y- через ooo, которое называется началом координат (точкой отсчета, от которой положение каждой другой точки на той же декартовой плоскости наблюдается).
Работа с горизонтальными и вертикальными линиями
Пример: Определить координаты точек пересечения линии y=2x+3y=2x+3y=2x+3 с горизонтальной линией y=3y=3y=3 и вертикальной линией х=2х=2х=2.
Решение. Пусть будет точкой пересечения прямой y=2x+3y=2x+3y=2x+3 с горизонтальной линией y=2y=2y=2 и QQQ с вертикальной линией x=2x=2x=2.
Пусть будет точкой пересечения прямой y=2x+3y=2x+3y=2x+3 с горизонтальной линией y=2y=2y=2 и QQQ с вертикальной линией x=2x=2x=2.
Таким образом, при подстановке y=2y=2y=2 в y=2x+3y=2x+3y=2x+3,
2=2x+3 ⇒ x=2−32=−122=2x+3\, \,\,\стрелка вправо \,\,\,x=\frac{2-3}{2}=-\frac{1}{2}2=2x+3⇒x=22−3=−21
Итак, координаты точки PPP равны (−12,2)\left( -\frac{1}{2},2 \right)(−21,2).
Опять же, подставив x=2x=2x=2 в y=2x+3y=2x+3y=2x+3,
y=2×2+3 ⇒ y=4+3=7y=2\times 2+3\,\,\,\стрелка вправо \,\,\,y=4+3=7y=2×2+ 3⇒y=4+3=7
Итак, координаты точки QQQ равны (2,4)\влево( 2,4 \вправо)(2,4).
Следовательно, координаты точек пересечения прямой y=2x+3y=2x+3y=2x+3 с горизонтальной линией y=2y=2y=2 и с вертикальной линией x=2x=2x=2 равны (−12,2)\left( -\frac{1}{2},2 \right)(−21,2) и (2,4)\left( 2,4 \right)(2,4) , соответственно.
Продолжайте учиться
Что изучать дальше на основе учебной программы колледжа
Форма точки пересечения наклона линииКоллинеарные точкиУравнение линии, параллельной заданной линииФорма линии с двумя точками пересечения: без наклонаОтрицательный наклонНулевой уклонСемейство линий
Добавить вертикальные и горизонтальные линии в график ggplot2 в R увидите, как добавить вертикальные и горизонтальные линии на график с помощью ggplot2 на языке программирования R.
 Добавление вертикальной линии к графику R с помощью функции geom_vline()
Добавление вертикальной линии к графику R с помощью функции geom_vline() Для добавления вертикальной линии к графику R, geom_vline() рисует вертикальную линию в указанной позиции.
Синтаксис: geom_vline(xintercept)
Параметр: здесь xintercept используется для управления положением линии по оси X.
Возврат: Вертикальная линия на графике R.
Пример: Чтобы добавить вертикальную линию на график, мы просто добавляем функцию geom_vline() в функцию ggplot2() и передаем xintercept , который в основном имеет положение на оси X, где мы фактически хотите создать вертикальную линию. Здесь мы ставим 2011 на xintercept.
R
|
:
:
:
: 2 . А для добавления горизонтальных линий к графику R мы будем использовать функцию geom_hline() : Синтаксис: Параметр: 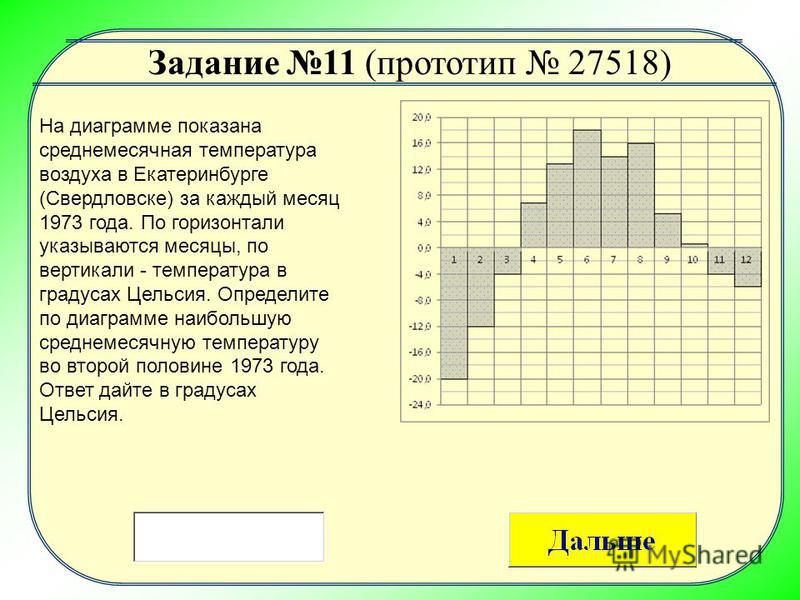 0003
0003
здесь yintercept используется для управления положением строки по оси y.
Возврат: Горизонтальная линия на графике R.
Пример: Чтобы добавить горизонтальную линию на график, мы просто добавляем geom_hline() в функцию ggplot2() и передать yintercept, который в основном имеет местоположение на оси Y , где мы фактически хотим создать вертикальную линию. Здесь мы устанавливаем 20 для xintercept.
R
| (THER, DATA). |
Выход:
Scatter Sline с Horizontal Line At y = 20
Scatter Scatter.
Чтобы добавить обе строки, мы добавляем функции geom_vline() и geom_hline() в функцию ggplot() и устанавливаем значения xintercept и yintercept.
Пример: Здесь мы проведем вертикальную линию в точке X=2012 и вертикальную линию в точке Y=20 .
R
|
Выход:
График рассеяния с обеими линиями при x = 2012 и y = 20
Добавление множества версии и y = 200003 Добавление множества версии и HORZONTALLY с использованием R -графика с r с r с r с r с r с r с r с r с r с r -графиками с использованием r с r с r с r с r с r с r с r с rs с использованием rs с использованием r -график. ) function Мы будем использовать функцию seq() для представления xintercept и yintercept , а все остальные настройки останутся такими же, как в примере 3.
Синтаксис: , seq(from, to )
Параметры:
- из: используется для представления начальной длины.
- to: используется для обозначения конечной длины.
- by: представляет собой приращение системы.
Возврат: корректная последовательность.
Пример: Здесь мы рисуем вертикальные линии от 2011 до 2015 с разницей 0,5 и горизонтальные линии от 10 до 50 с разницей 5 .
R
|

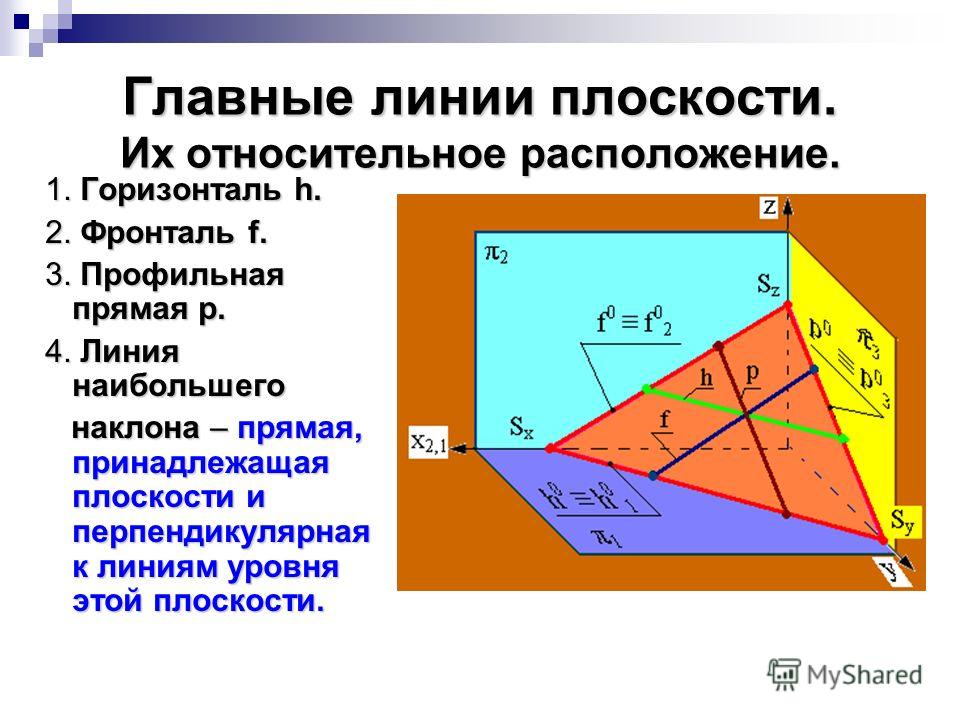 Как расположена линия горизонта? Горизонтально. Чему? Земле.
Как расположена линия горизонта? Горизонтально. Чему? Земле.
 шоу()
шоу()
 express как px
df = px.data.stocks(indexed=True)
рис = px.line (df)
fig.add_hline(y=1, line_dash="точка",
annotation_text="1 января 2018 г. – базовый уровень",
annotation_position="внизу справа")
fig.add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
express как px
df = px.data.stocks(indexed=True)
рис = px.line (df)
fig.add_hline(y=1, line_dash="точка",
annotation_text="1 января 2018 г. – базовый уровень",
annotation_position="внизу справа")
fig.add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
 add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
аннотация = dict (font_size = 20, font_family = "Times New Roman"),
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
add_vrect(x0="2018-09-24", x1="2018-12-18",
annotation_text="отклонение", annotation_position="вверху слева",
аннотация = dict (font_size = 20, font_family = "Times New Roman"),
fillcolor="зеленый", непрозрачность=0,25, line_width=0)
рис.шоу()
 шоу()
шоу()
 .. )
# fig.update_layout( ... )
импортировать тире
импортировать dash_core_components как DCC
импортировать dash_html_components как html
приложение = тире.Dash()
app.layout = html.Div([
dcc.Graph(рисунок=рис)
])
app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter
.. )
# fig.update_layout( ... )
импортировать тире
импортировать dash_core_components как DCC
импортировать dash_html_components как html
приложение = тире.Dash()
app.layout = html.Div([
dcc.Graph(рисунок=рис)
])
app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter

 FRAME
FRAME  FRAME
FRAME 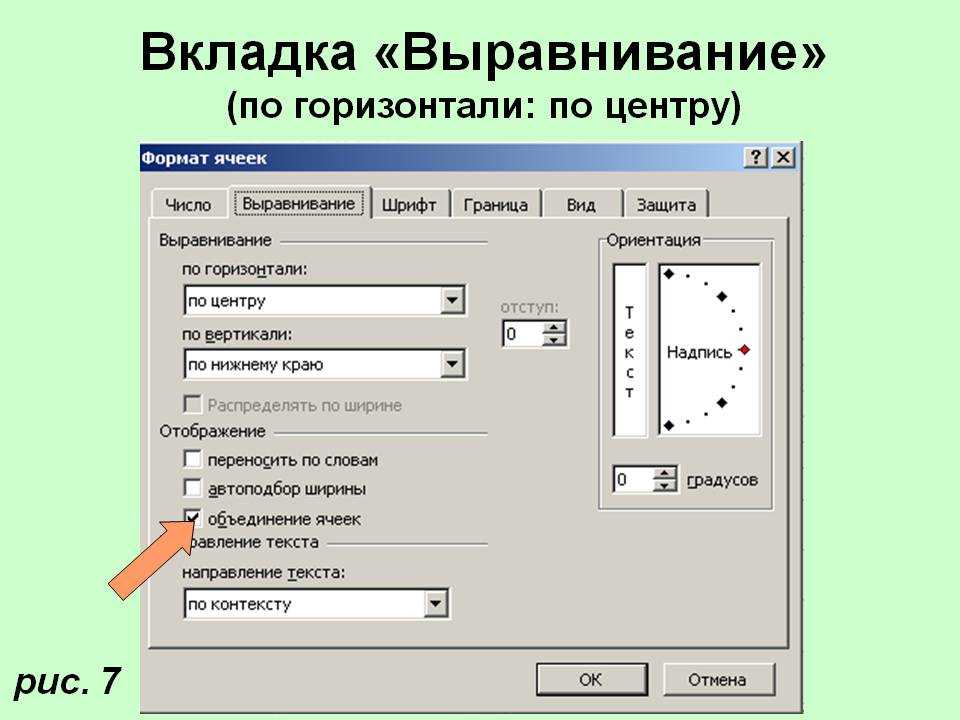 (
( 