Матричные фильтры обработки изображений / Habr
Данная статья рассказывает не только о наиболее распространённых фильтрах обработки изображений, но в понятной форме описывает алгоритмы их работы. Статья ориентирована, прежде всего, на программистов, занимающихся обработкой изображений.Матрица свёртки
Фильтров использующих матрицу свёртки много, ниже будут описаны основные из них.
Матрица свёртки – это матрица коэффициентов, которая «умножается» на значение пикселей изображения для получения требуемого результата.
Ниже представлено применение матрицы свёртки:
div – это коэффициент нормирования, для того чтобы средняя интенсивность оставалась не изменой.
В примере матрица имеет размер 3×3, хотя размер может быть и больше.
Фильтр размытия
Наиболее часто используемым фильтром, основанным на матрице свёртки, является фильтр размытия.
Обычно матрица заполняется по нормальному (гауссовому закону). Ниже приведена матрица размытия 5×5 заполненная по закону Гауссовского распределения.
Коэффициенты уже являются нормированными, так что div для этой матрицы равен одному.
От размера матрицы зависит сила размытия.
Стоит упомянуть о граничных условиях (эта проблема актуальна для всех матричных фильтров). У верхнего левого пикселя не существует «соседа» с права от него, следовательно, нам не на что умножать коэффициент матрицы.
Существует 2 решения этой проблемы:
1. Применение фильтра, только к «окну» изображения, которое имеет координаты левого верхнего угла [kernelSize / 2, kernelSize / 2], а для правого нижнего [width — kernelSize / 2, height — kernelSize / 2]. kernelSize – размер матрицы; width, height – размер изображения.
Это не лучший способ, так как фильтр не применяется ко всему изображению. Качество при этом довольно сильно страдает, если размер фильтра велик.
2. Второй метод (дополнение) требует создания промежуточного изображения. Идея в том, чтобы создавать временное изображение с размерами (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). В центр изображения копируется входная картинка, а края заполняются крайними пикселями изображения. Размытие применяется к промежуточному буферу, а потом из него извлекается результат.
Данный метод не имеет недостатков в качестве, но необходимо производить лишние вычисления.
Фильтр размытия по Гауссу имеет сложность O(hi * wi * n *n), где hi, wi – размеры изображения, n – размер матрицы (ядра фильтра). Данный алгоритм можно оптимизировать с приемлемым качеством.
Квадратное ядро (матрицу) можно заменить двумя одномерными: горизонтальным и вертикальным. Для размера ядра 5 они будут иметь вид:
Фильтр применяется в 2 прохода: сначала горизонтальный, а потом к результату вертикальный (или на оборот).
Сложность данного алгоритма будет O(hi * wi * n) + O(hi * wi * n) = 2 * O(hi * wi * n), что для размера ядра больше двух, быстрее, чем традиционный метод с квадратной матрицей.
Фильтр улучшения чёткости
Для улучшения четкости необходимо использовать следующую матрицу:
Эта матрица увеличивает разницу значений на границах. Div для этой матрицы равен 1.
В программе GIMP есть фильтр «Матрица свёртки», который упрощает поиск необходимого Вам матричного преобразования.
Более подробную информацию о фильтрах основанных на матрице свёртки вы можете найти в статье «Графические фильтры на основе матрицы скручивания».
Медианный фильтр
Медианный фильтр обычно используется для уменьшения шума или «сглаживания» изображения.
Фильтр работает с матрицами различного размера, но в отличие от матрицы свёртки, размер матрицы влияет только на количество рассматриваемых пикселей.
Алгоритм медианного фильтра следующий:
Для текущего пикселя, пиксели, которые «попадают» в матрицу, сортируются, и выбирается средние значение из отсортированного массива. Это значение и является выходным для текущего пикселя.
Ниже представлена работа медианного фильтра для размера ядра равного трём.
Фильтры эрозия и наращивание
Фильтры наращивание и эрозия служат для получения морфологического расширения или сужения соответственно. Проще говоря, для изображений это значит выбор пикселя с максимальной или минимальной интенсивностью из окрестности.
В результате наращивания происходит увеличение ярких объектов, а эрозии – увеличение тёмных объектов.
Фильтр использует входное изображение и бинарную матрицу. Бинарная матрица определяет форму окрестности. Обычно окрестность имеет круглую форму.
Фильтр наращивание может быть использован для увеличения бликов, ярких отражений.
Заключение
В статье были описаны некоторые из фильтров обработки изображения, описаны их алгоритмы и особенности применения.
ru.wikipedia.org/wiki/Медианный_фильтр
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Математическая_морфология
habrahabr.ru/post/43895
Использование CSS-фильтров для придания изображениям различных эффектов

От автора: используя изображения, мы можем создать атмосферу, вызвать счастье, улыбку, грусть или любую другую эмоцию. С помощью изображений мы можем многое показать, а также многое рассказать; именно поэтому изображения так широко используются на сайтах и в приложениях.
Дизайнеры заботятся о том, как пользователи будут воспринимать сайт и какие эмоции он будет вызывать. Графические дизайнеры могут использовать передовое программное обеспечение для редактирования фотографий и добавления к ним фильтры, маски или другие эффекты, которые определяют окончательный вид.
Иногда бывает так, что то, что было разработано дизайнером, сложно кодировать, и как разработчики мы обращаем внимание на производительность кода и хотим, чтобы сайты загружались быстро. Это часто означает, что мы должны уменьшить размер изображения. Это также причина, по которой мы предпочитаем воспроизводить эффекты, созданные дизайнером, используя код. Особенно, когда нам нужно добавить эффект при наведении или клике, мы не хотим загружать два изображения.
Мы можем использовать код для простого добавления фильтров к изображениям, например, с помощью CSS, и в этой статье я хотел бы показать вам, как вы можете использовать фильтры для создания потрясающего эффекта. Давайте начнем!
Фильтры в CSS
Чтобы создать фильтры для изображений в CSS, мы используем свойство filter, которое определяет визуальные эффекты, используя несколько различных функций. Каждая функция может дать различный результат для основного изображения. Также возможно добавить к одному изображению несколько фильтров.

Практический курс по верстке адаптивного сайта с нуля!
Изучите курс и узнайте, как верстать современные сайты на HTML5 и CSS3
Узнать подробнееДавайте рассмотрим, какой результат мы можем получить.
1. grayscale(% | number)
Самый популярный фильтр, добавляемый к изображениям — это оттенки серого. Он позволяет создавать черно-белые фотографии. Функция оттенков серого может принимать аргументы в процентах или числах. 0% означает, что ничего не изменится, а 100% означает, что изображение будет полностью преобразовано в оттенки серого. Если вы оставите значение пустым, оно по умолчанию будет 100%. Если вы хотите установить значение числом, оно может быть от 0 до 1.
В приведенном выше примере вы можете увидеть исходную фотографию без каких-либо фильтров, вторая — это изображение со значением 0,5, а последняя — полностью черно-белая фотография.
2. sepia(% | number)
Фильтр sepia создает красновато-коричневую цветную фотографию. Метод sepia() работает аналогично оттенкам серого; он также принимает значения от 0% до 100% или от 0 до 1. Отрицательные значения не допускаются. Давайте рассмотрим на примеры:
В примере выше вы можете увидеть, как работает фильтр сепия. Я думаю, что это хороший вариант для создания фотографий под ретро. Это то, что пришло мне в голову после просмотра изображения сепии.
3. blur(px)
Эффект размытия делает фотографию очень размытой, применяя эффект размытия по Гауссу. Это применимо к скрытым по соображениям цензуры фрагментов или фоновым изображениям, когда нет необходимости делать фотографию очень четкой. Метод blur() также принимает один аргумент — определенное количество пикселей. Чем больше значение — тем больше размытие. По умолчанию значение равно 0.
Первый пример — базовое изображение без фильтра, второй — с размытием в 2 пикселя, а в последнем практически невозможно распознать, что на фото.
4. brightness(% | number)
Еще один фильтр — brightness(), позволяющий регулировать уровень яркости картинки. Он принимает один параметр в процентах от 0% до 100% — чем выше значение, тем ярче изображение — или число от 0 до 1. По умолчанию яркость каждого изображения составляет 100%. Давайте посмотрим, как этот фильтр ведет себя на примере кода:
Изображения в примере имеют яркость от 0,5 и до 150%.

Практический курс по верстке адаптивного сайта с нуля!
Изучите курс и узнайте, как верстать современные сайты на HTML5 и CSS3
Узнать подробнее5. contrast(% | number)
Фильтр contrast() позволяет задать контрастность изображений. Если установлено значение 0% или число 0, оно будет полностью темным. По умолчанию установлено 100% или 1, что означает, что фотография не будет изменена вообще, а значения выше 100% или 1 задают меньшую контрастность. Давайте посмотрим на пример:
В приведенном выше коде я уменьшил контрастность первой картинки до 10%, а для второй фотографии задал 200%.
6. saturate(% | number)
saturate описывает интенсивность цветов, и чем больше значение фильтра, тем ярче цвета. Значение по умолчанию для изображения составляет 100% или 1, 0 означает, что изображение является ненасыщенным, а все значения выше 100% и 1 увеличивают насыщенность. Давайте посмотрим на пример:
Как вы можете видеть в примере, второе изображение ненасыщено, для него установлено 20%, а третье изображение имеет насыщенность 200%, и оно заметно ярче других.
7. hue-rotate(deg)
Во-первых, давайте сначала объясним, что такое поворот оттенка, потому что это может сбивать вас с толку. Как сбивало в свое время меня. Итак, поворот оттенка — это функция, в которой мы указываем угол на круговой диаграмме цветов. Он может указываться в градусах или оборотах. Он также принимает отрицательные значения. Максимальное значение составляет 360 градусов, поэтому даже если мы установим большее значение, оно будет работать, как в круге, например, если вы установите 450 градусов, результат будет такой же, как для 90 градусов, а если мы введем -10 градусов, результат будет аналогичен 350 градусов (360 градусов — 10 градусов). Давайте посмотрим на пример кода:
В приведенном выше примере вы можете видеть четыре изображения, первое из которых является оригинальным, без какого-либо поворота оттенка, оно выглядит так же как изображение с поворотом оттенка в 360 градусов. Для второго изображения установлено 90 градусов поворота оттенка, и видно, что зеленый здесь очень интенсивный. Третье изображение имеет 180 градусов, и в этом примере изображение более голубое, а последнее имеет -90 градусов (что аналогично 240 градусов), оно является более красноватым.
8. invert(% | number)
Еще один фильтр, который может быть применен к изображениям с использованием CSS — это invert. Он используется для инвертирования цветов на изображении. Значение, которое принимает функция invert, может быть только положительным. Давайте посмотрим на пример:
В приведенном выше коде вы можете видеть три изображения. Первое является оригинальным, следующее инвертируется до 75%, а последний полностью инвертируется (значение равно 1).
Заключение
Добавление фильтров к изображениям иногда весьма удобно, особенно если вы хотите добиться удивительного визуального эффекта.
В этой статье я представил 8 методов фильтров и описал значения, которые они принимают, чтобы вы могли просто взглянуть и узнать, какой фильтр применить, чтобы получить требуемый результат.
Я надеюсь, что вы найдете это полезным, также поделитесь своими любимыми методами фильтров в комментариях, или, может быть, вы создали какие-то потрясающие пользовательские фильтры? Дайте мне знать! Удачного кодирования!
Автор: Duomly
Источник: https://dev.to
Редакция: Команда webformyself.

Практический курс по верстке адаптивного сайта с нуля!
Изучите курс и узнайте, как верстать современные сайты на HTML5 и CSS3
Узнать подробнее
PSD to HTML
Верстка сайта на HTML5 и CSS3 с нуля
СмотретьФильтрация изображений на C# — Программирование на C, C# и Java
Представляем вашему вниманию исходник программы для простой фильтрации растровых изображений, позволяющей изменять яркость, контрастность, цветовой баланс картинки, а также повышать резкость и размывать изображения. Кроме того, будут описаны алгоритмы для работы с графикой, используемые в программе.
Теоретические сведения
Фильтр «Яркость/контрастность»
Для изменения яркости на N процентов используется следующая формула:
I = I + N • 128 / 100 (1)
где I – соответственно R, G, B каналы каждой точки изображения.
I = (I • (100 – N) + 128 • N) / 100 (2)
Увеличение контрастности на N процентов:
I = (I • 100 – 128 • N) / (100 – N) (3)
Если новое I не попадает в диапазон 0..255 – то его следует урезать.
Фильтр «Цветовой баланс»
Для изменения цветового баланса по одному из каналов R, G, B на N процентов следует вычислить новое значение цветового канала по формуле:
I = I + N • 128 / 100, где I – это R, G или B каждой точки изображения. (4)
Если новое I не попадает в диапазон 0..255 – то его следует урезать.
Фильтры «Повысить резкость» и «Размыть»
Эти фильтры реализуются на основе ядра свертки. Элемент изображения получает новое значение на основе группы элементов, примыкающих к данному. Область примыкания есть квадратная матрица, размерность которой совпадает с размером выбранного ядра свертки, и центром в обрабатываемом элементе.
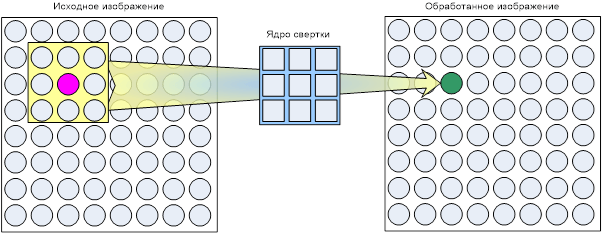
Ядро свертки представляет собой матрицу размером 3х3, 5х5, 7х7 и т.д., на которой определена некоторая функция. Ядро свертки называется окном, а заданная на нем функция – весовой или функцией окна. Каждому элементу окна соответствует число, называемое весовым множителем. Совокупность всех весовых множителей и составляет весовую функцию. Нечетные размеры окна необходимы для однозначного определения центрального элемента.
По сути, ядро свертки является фильтром, который позволяет усилить или ослабить компоненты изображения. Фильтрация осуществляется перемещением окна фильтра по изображению. Весовая функция в процессе перемещения остается неизменной. В каждом положении окна происходит операция свертки – линейная комбинация значений элементов изображения:

При каждом положении окна весовая функция поэлементно умножается на значение соответствующих пикселей исходного изображения и произведения суммируются. Полученная сумма называется откликом фильтра и присваивается тому пикселю нового изображения, который соответствует положению центра окна.
Результат обработки пикселя записывается в соответствующую ячейку временной матрицы такого же размера, как и исходное изображение. Запись в отдельную временную матрицу необходима для того, чтобы исключить влияние уже обработанных пикселей на еще не обработанные.
Обязательно следует упомянуть о граничных условиях. Например, у верхнего левого пикселя не существует «соседей» слева и сверху, следовательно, нам не на что умножать коэффициенты матрицы.
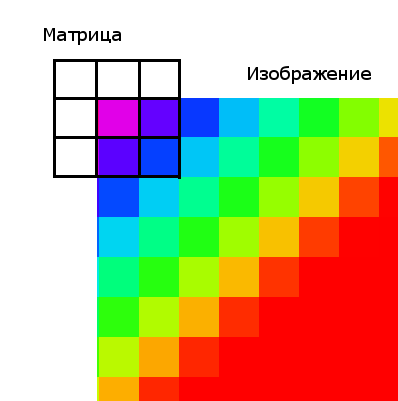
Для решения этой проблемы требуется создание промежуточного изображения. Идея в том, чтобы создавать временное изображение с размерами (width + 2 • gap / 2, height + 2 • gap / 2, где width и height – ширина и высота фильтруемого изображения, а gap – размерность матрицы свертки). В центр изображения копируется входная картинка, а края заполняются крайними пикселями изображения. Размытие применяется к промежуточному буферу, а потом из него извлекается результат.
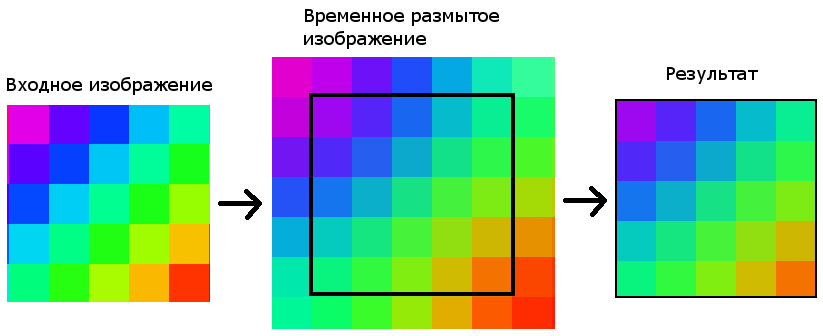
При использовании алгоритма увеличения резкости подчеркиваются различия между цветами смежных пикселей и выделяются незаметные детали. В ядре резкости центральный коэффициент больше 1, а окружен он отрицательными числами, сумма которых на единицу меньше центрального коэффициента. Таким образом, увеличивается любой существующий контраст между цветом пикселя и цветами его соседей. При обработке каждого пикселя в изображении используется ядро резкости размерами 3×3:
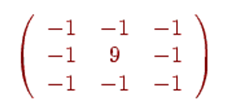
При использовании алгоритма размытия в изображении перераспределяются цвета и смягчаются резкие границы. Ядро сглаживания состоит из совокупности коэффициентов, каждый из которых меньше 1, а их сумма составляет 1. Это означает, что после фильтрации каждый пиксель поглотит что-то из цветов соседей, но полная яркость изображения останется неизменной. При обработке изображения используется следующее ядро свертки:
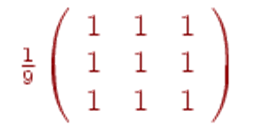
Описание алгоритмов
Изменение яркости
В функцию изменения яркости передается значение цвета текущего пикселя, текущее положение ползунка (poz) изменения яркости и максимальное значение, которое он может принимать (length).
1) Вычисляется количество процентов N = (100 / lenght) * poz.
2) По формуле (1) для каждого цветового канала рассчитывается новое значение.
3) Контролируем переполнение переменных:
ЕСЛИ I < 0, ТО I = 0,
ЕСЛИ I > 255, ТО I = 255,
где I – соответственно R, G, B пикселя.
4) return значения цвета пикселя.
Изменение контрастности
В функцию изменения контрастности передается значение цвета текущего пикселя, текущее положение ползунка (poz) изменения контрастности и максимальное значение, которое он может принимать (length).
1) Вычисляется количество процентов N = (100 / lenght) * poz.
2) ЕСЛИ N < 0, то новое значение цвета каждого канала рассчитывается (N берется по модулю) по формуле (2)
ИНАЧЕ по формуле (3).
3) Контролируем переполнение переменных:
ЕСЛИ I > 255, ТО I = 255,
где I – соответственно R, G, B пикселя.
4) return значения цвета пикселя.
Изменение цветового баланса
В функцию изменения цветового баланса по соответствующему каналу передается значение цвета текущего пикселя, текущее положение ползунка (poz) изменения цветового баланса и максимальное значение, которое он может принимать (length).
1) Вычисляется количество процентов N = (100 / lenght) * poz.
2) По формуле (4) для соответствующего цветового канала рассчитывается новое значение.
3) Контролируем переполнение переменных:
ЕСЛИ I < 0, ТО I = 0,
ЕСЛИ I > 255, ТО I = 255,
где I – соответствующий (R, G или B) канал цвета пикселя.
4) return значения цвета пикселя.
Повышение резкости и размытие
В функцию передаются значения ширины и высоты редактируемого изображения, матрица пикселей этого изображения, размерность матрицы свертки и сама матрица.
1) Создание временной матрицы расширенного изображения и ее заполнение.
2) Применение ядра свертки для каждого пикселя, при этом контролируем переполнение переменных (0…255 для каждого канала). Новые значения цветов пикселей заносятся в отдельную матрицу (newpixel)
3) Возвращение функцией матрицы newpixel.
Описание структуры ПО
Для построения пользовательского интерфейса применяется графиче-ская подсистема Windows Forms. Во время выполнения программы используются классы Form1, Form2, Form3, BrightnessContrast, ColorBalance, Filter, которые включают следующие методы:
Brightness – метод, изменяющий яркость текущей точки.
Contrast – метод, изменяющий контрастность текущей точки.
ColorBalance_R – метод, изменяющий цветовой баланс точки по каналу R.
ColorBalance_B – метод, изменяющий цветовой баланс точки по каналу B.
matrix_filtration – метод, выполняющий фильтрацию изображения на основе ядра свертки.
Описание структуры пользовательского интерфейса

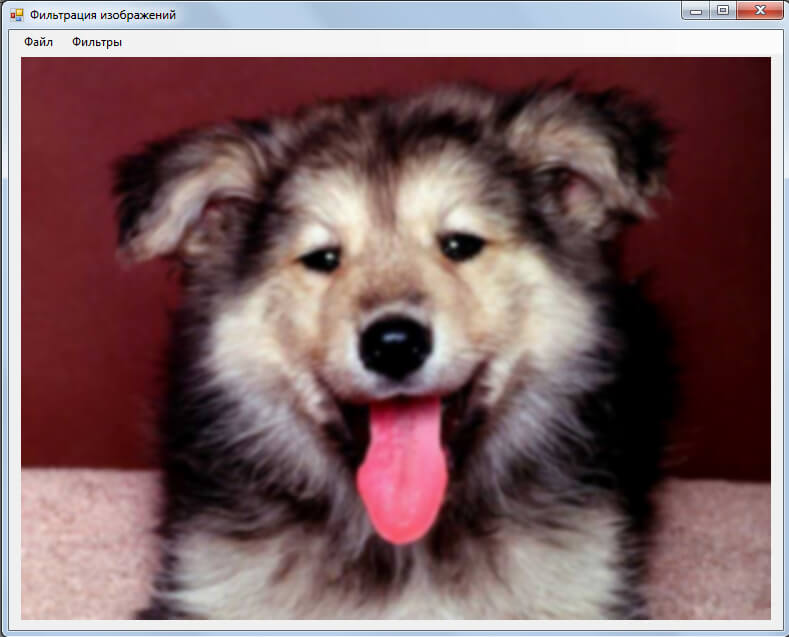
На рисунках выше представлено главное меню программы. Во вкладке «Файл» находятся кнопки для открытия и сохранения изображения. Во вкладке «Фильтры» представлены инструменты для фильтрации загруженного изображения: «Яркость/контрастность», «Цветовой баланс», «Повысить резкость», «Размыть». При вызове первых двух открываются новые окна, в которых находятся слайдеры для изменения соответствующих компонентов фильтруемого изображения и кнопки «Применить», для сохранения изменений:
Демонстрация работы программы
Исходное изображение:

Изменение яркости:
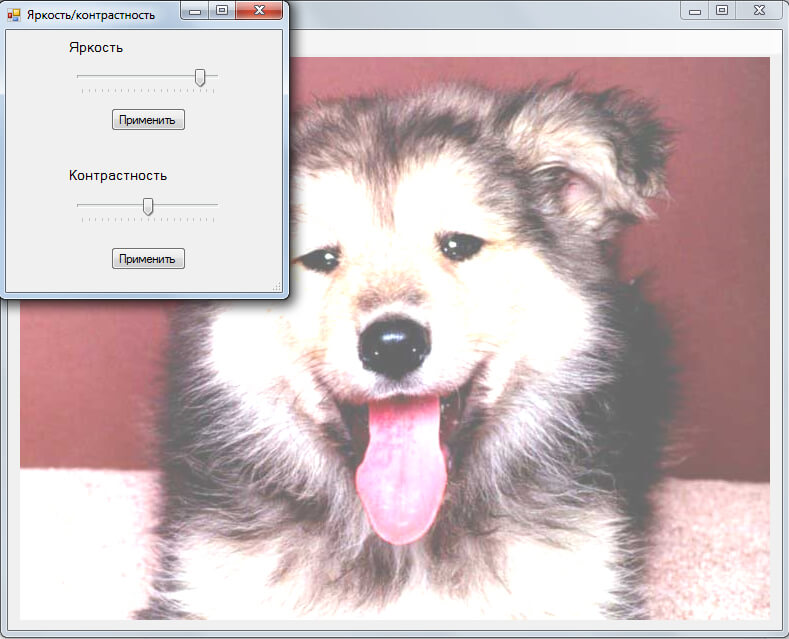
Изменение контрастности:
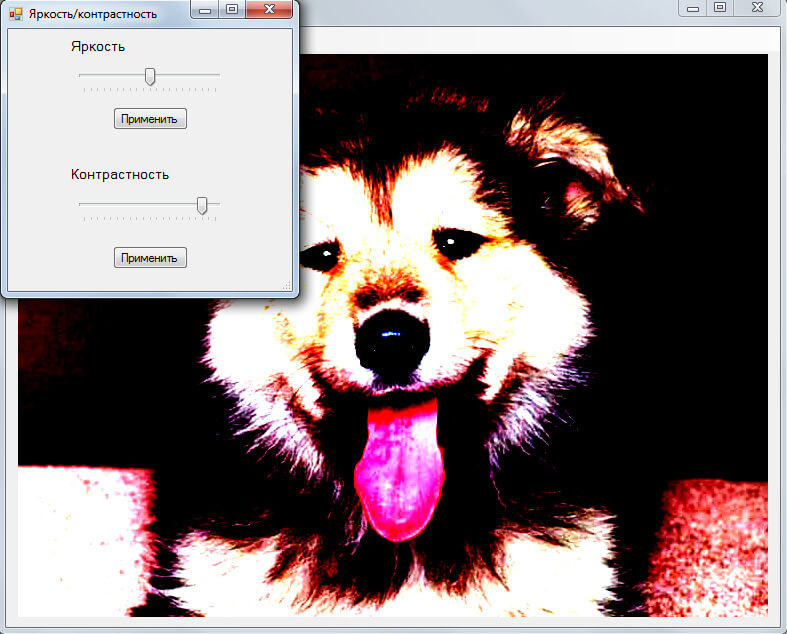
Изменение цветового баланса:
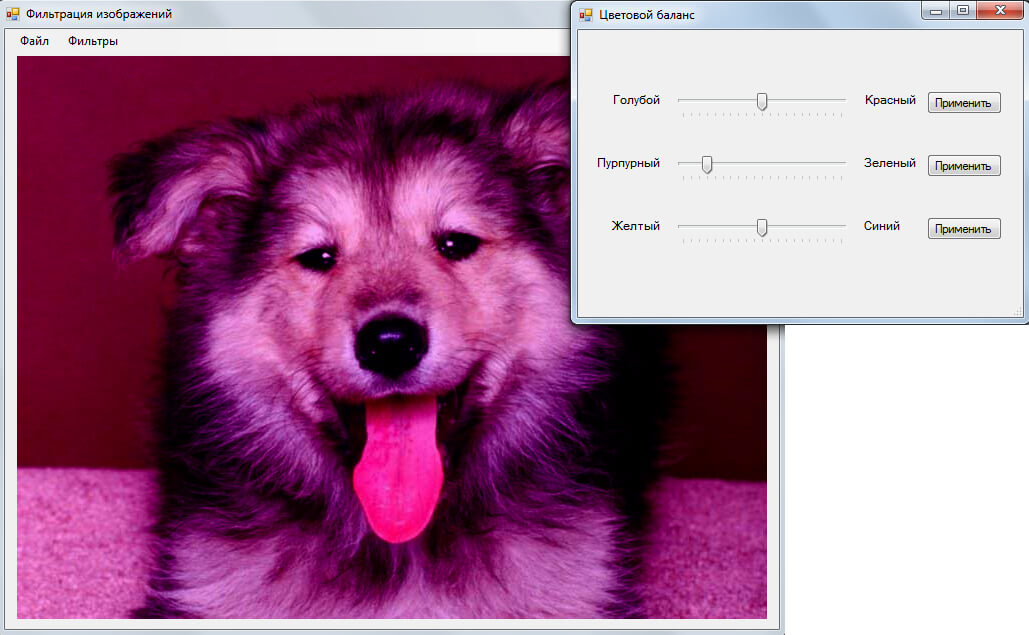
Повышение резкости:
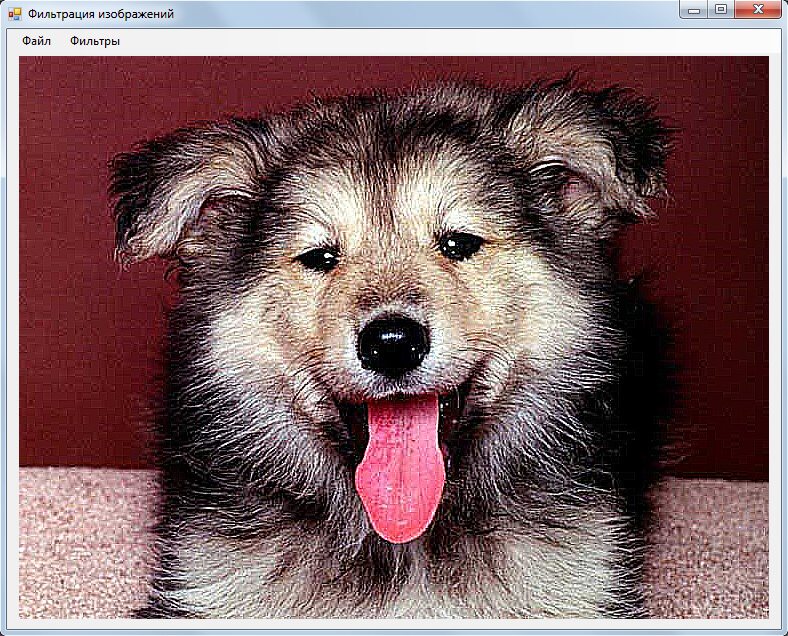
Размытие изображения:
Скачать исходник программы можно, нажав на кнопку ниже:
Скачать исходник
Фильтрация изображений на C#
5 (100%) 10 votes
Поделиться в соц. сетях:
НОУ ИНТУИТ | Лекция | Фильтрация изображений
Аннотация: Введение. Линейные фильтры: определение, сглаживающие фильтры, контрастоповышающие фильтры, разностные фильтры. Нелинейные фильтры: примеры нелинейных фильтров, морфологические операторы
8.1. Введение
Представим себе, что, глядя на какую-нибудь сцену одним глазом, мы подносим к нему стеклянную пластину. Если эта пластина не была идеально прозрачной, то наблюдаемое изображение изменится. В зависимости от стекла, из которого сделана пластина, изменение может быть самым разнообразным. К примеру, если это стекло было цветным, то изображение приобретет соответствующий оттенок, а от мутного стекла — станет размытым.
Фильтрация изображений аналогична такому разглядыванию мира через стеклянную пластину, хотя и позволяет добиться гораздо большего разнообразия эффектов, чем эксперименты с разными пластинами. Под фильтрацией изображений понимают операцию, имеющую своим результатом изображение того же размера, полученное из исходного по некоторым правилам. Обычно интенсивность (цвет) каждого пикселя результирующего изображения обусловлена интенсивностями (цветами) пикселей, расположенных в некоторой его окрестности в исходном изображении.
Правила, задающие фильтрацию (их называют фильтрами ), могут быть самыми разнообразными. В этой лекции мы рассмотрим простейшие фильтры. Заметим, что, согласно предложенному определению, операция, заключающаяся в последовательном применении двух или более фильтраций, тоже является фильтрацией. Таким образом, можно говорить о составных фильтрах, соответствующих комбинациям простых. Изучив основные типы фильтров в данной лекции, мы будем иметь дело с применением фильтров, составленных из них, для решения разнообразных задач в последующих лекциях. Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов. Рассматриваемые в этой лекции фильтры имеют, таким образом, чрезвычайную важность с точки зрения их применения в различных приложениях.
8.2. Линейные фильтры
Определение
Линейные фильтры представляют собой семейство фильтров, имеющих очень простое математическое описание. Вместе с тем они позволяют добиться самых разнообразных эффектов. Будем считать, что задано исходное полутоновое изображение A, и обозначим интенсивности его пикселей A(x, y). Линейный фильтр определяется вещественнозначной функцией F, заданной на растре. Данная функция называется ядром фильтра, а сама фильтрация производится при помощи операции дискретной свертки (взвешенного суммирования) (см. также «Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений» ):
| ( 8.1) |
Результатом служит изображение B. В определении (8.1) мы опустили пределы суммирования. Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности F(i, j) или в точности равно нулю, или очень близко к нему, так что можно им пренебречь. Суммирование в (8.1) производится по , и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей Mkl, ее следует центрировать:
| ( 8.2) |
Также нуждается в дополнительном прояснении ситуация, когда пиксель (x, y) находится в окрестности краев изображения. В этом случае A(x + i, y + j) в определении (8.1) может соответствовать пикселю A, лежащему за пределами изображения A. Данную проблему можно разрешить несколькими способами.
- Не проводить фильтрацию для таких пикселей, обрезав изображение B по краям или закрасив их, к примеру, черным цветом.
- Не включать соответствующий пиксель в суммирование, распределив его вес F(i, j) равномерно среди других пикселей окрестности N(x, y).
- Доопределить значения пикселей за границами изображения при помощи экстраполяции. Например, считать постоянным значение интенсивности вблизи границы (для пикселя (-2, 5) имеем A(-2, 5) = A(0, 5) ) или считать постоянным градиент интенсивности вблизи границы ( A(-2, 5) = A(0, 5) + 2(A(0, 5) — A(1, 5)) ).
- Доопределить значения пикселей за границами изображения, при помощи зеркального отражения ( A(-2, 5) = A(2, 5) ).
Выбор конкретного способа нужно производить с учетом конкретного фильтра и особенностей конкретного приложения.
Разобрав общее определение линейных фильтров, перейдем к примерам.
17.3. Фильтрация изображений [49, 1i]
Под фильтрацией изображений понимают операцию, имеющую своим результатом изображение того же размера, полученное из исходного по некоторым правилам. Обычно интенсивность (цвет) каждого пикселя результирующего изображения обусловлен интенсивностями (цветами) пикселей, расположенных в некоторой его окрестности в исходном изображении.
Правила фильтрации могут быть самыми разнообразными. Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. С той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов обработки изображений.
Линейные фильтрыимеют очень простое математическое описание. Будем считать, что задано исходное полутоновое изображение A, и обозначим интенсивности его пикселей A(x, y). Линейный фильтр определяется вещественнозначной функцией h (ядром фильтра), заданной на растре. Сама фильтрация производится при помощи операции дискретной свертки (взвешенного суммирования):
B(x, y) =
h(i, j) ③③A(x,
y) = 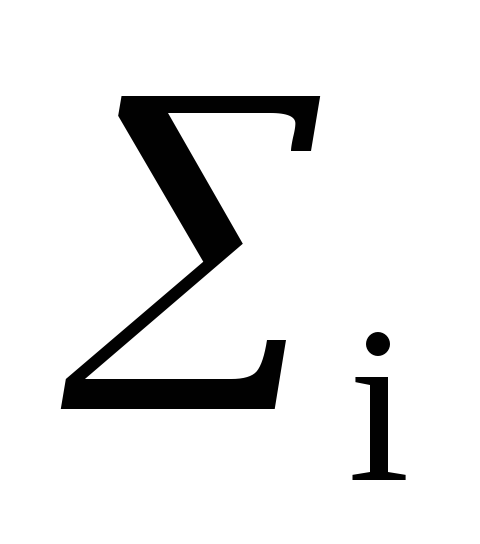
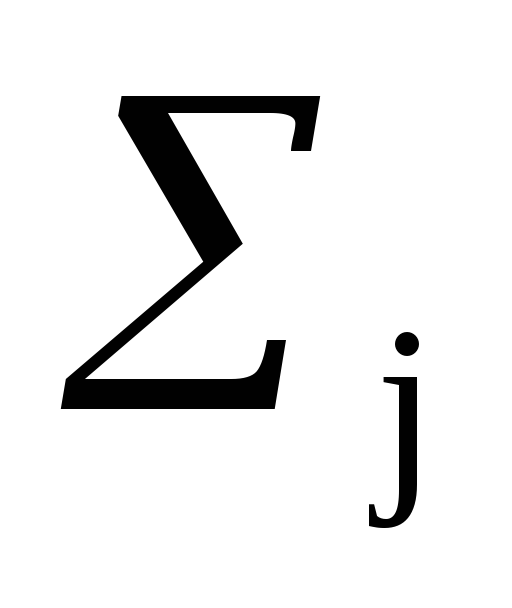 h(i,
j) A(x-i, y-j). (17.3.1)
h(i,
j) A(x-i, y-j). (17.3.1)
Результатом служит изображение B. Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности h(i, j) равно нулю, или очень близко к нему и им можно пренебречь. Суммирование производится по (i, j) N, и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (обозначение — множество N(x, y)). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей ее следует центрировать. Если пиксель (x, y) находится в окрестности краев изображения, то координаты A(x-i, y-j) для определенных (i, j) могут соответствовать несуществующим пикселям A за пределами изображения. Данную проблему можно разрешить несколькими способами.
— Не проводить фильтрацию для таких пикселей, обрезав изображение B по краям, или применив для их значений исходные значения изображения А.
— Не включать отсутствующий пиксель в суммирование, распределив его вес h(i, j) равномерно среди других пикселей окрестности N(x, y).
— Доопределить значения пикселей за границами изображения при помощи экстраполяции.
— Доопределить значения пикселей за границами изображения, при помощи зеркального продолжения изображения.
Выбор способа производится с учетом конкретного фильтра и особенностей изображения.
Сглаживающие фильтры. Простейший прямоугольный сглаживающий фильтр радиуса r задается при помощи матрицы размера (2r+1) × (2r+1), все значения которой равны 1/(2r+1)2, а сумма значений равна единице. Это двумерный аналог низкочастотного одномерного П-образного фильтра скользящего среднего. При фильтрации с таким ядром значение пикселя заменяется усредненным значением пикселей в квадрате со стороной 2r+1 вокруг него. Пример маски фильтра 3× 3:
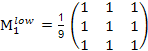 .
.
Одним из применений фильтров является шумоподавление. Шум меняется независимо от пикселя к пикселю и, при условии, что математическое ожидание значения шума равно нулю, шумы соседних пикселей при суммировании будут компенсировать друг друга. Чем больше окно фильтрации, тем меньше будет усредненная интенсивность шума, однако при этом будет происходить и соответствующее размытие значащих деталей изображения. Образом белой точки на черном фоне при фильтрации (реакция на единичный импульс) будет равномерно серый квадрат.
Шумоподавление при помощи прямоугольного фильтра имеет существенный недостаток: все пиксели в маске фильтра на любом расстоянии от обрабатываемого оказывают на результат одинаковый эффект. Несколько лучший результат получается при модификации фильтра с увеличением веса центральной точки:
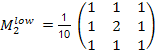 .
.
Более эффективное шумоподавление можно осуществить, если влияние пикселей на результат будет уменьшаться с увеличением расстояния от обрабатываемого. Этим свойством обладает гауссовский фильтр с ядром: h(i, j) = (1/22) exp(-(i2+j2)/2 Гауссовский фильтр имеет ненулевое ядро бесконечного размера. Однако значения ядра фильтра очень быстро убывает к нулю при удалении от точки (0, 0), и потому на практике можно ограничиться сверткой с окном небольшого размера вокруг (0, 0), например, взяв радиус окна равным 3σ.
Гауссовская фильтрация также является сглаживающей. Однако, в отличие от прямоугольного фильтра, образом точки при гауссовой фильтрации будет симметричное размытое пятно, с убыванием яркости от середины к краям. Степень размытия изображений определяются параметром σ.
Контрастоповышающие фильтры. Если сглаживающие фильтры снижают локальную контрастность изображения, размывая его, то контрастоповышающие фильтры производят обратный эффект и, по существу, являются фильтрами высоких пространственных частот. Ядро контрастоповышающего фильтра в точке (0, 0) имеет значение, большее 1, при общей сумме значений, равной 1. Например, контрастоповышающими фильтрами являются фильтры с ядром, задаваемым матрицами:
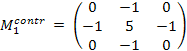 .
. 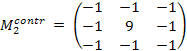 .
.

Рис. 17.3.1.
Пример применения фильтра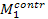 приведен
на рис. 17.3.1. Эффект повышения контраста
достигается за счет того, что фильтр
подчеркивает разницу между интенсивностями
соседних пикселей, удаляя эти интенсивности
друг от друга. Этот эффект будет тем
сильней, чем больше значение центрального
члена ядра. Характерным артефактом
линейной контрастоповышающей фильтрации
являются заметные светлые и менее
заметные темные ореолы вокруг границ.
приведен
на рис. 17.3.1. Эффект повышения контраста
достигается за счет того, что фильтр
подчеркивает разницу между интенсивностями
соседних пикселей, удаляя эти интенсивности
друг от друга. Этот эффект будет тем
сильней, чем больше значение центрального
члена ядра. Характерным артефактом
линейной контрастоповышающей фильтрации
являются заметные светлые и менее
заметные темные ореолы вокруг границ.Разностные фильтры – это линейные фильтры, задаваемые дискретными аппроксимациями дифференциальных операторов (по методу конечных разностей). Данные фильтры играют важнейшую роль во многих приложениях, например, для задач поиска границ на изображении.
Простейшим дифференциальным оператором является взятие производной по x-координате d/dx, который определен для непрерывных функций. Распространенными вариантами аналогичных операторов для дискретных изображений являются фильтры Прюита (Prewitt) и Собеля (Sobel):
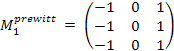 .
. 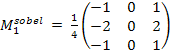 .
.
Фильтры, приближающие оператор производной по y-координате d/dy, получаются путем транспонирования матриц.
Простейший алгоритм вычисления нормы градиента по трем смежным точкам:
G(x,
y)
=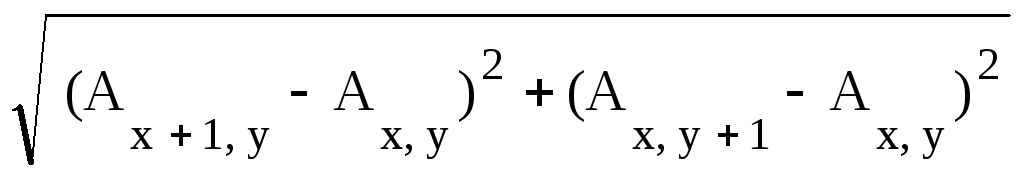 .
.
Применяется также упрощенная формула вычислений:
G(x,
y)
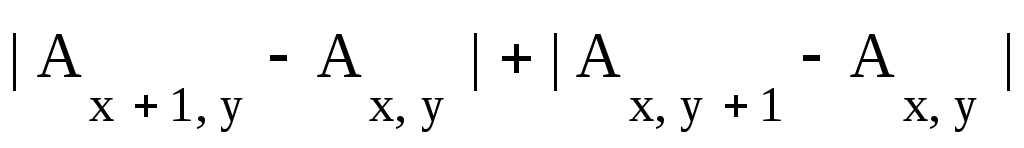 .
.
Вычисление нормы градиента по четырем смежным точкам (оператор Робертса):
G(x,
y)
=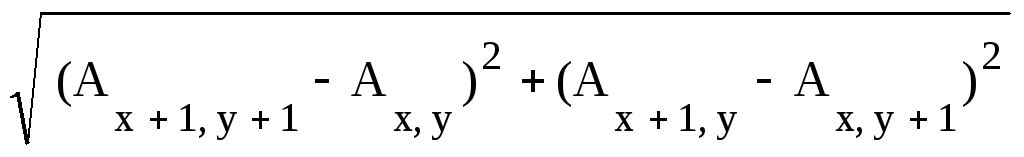 .
.
G(x,
y)
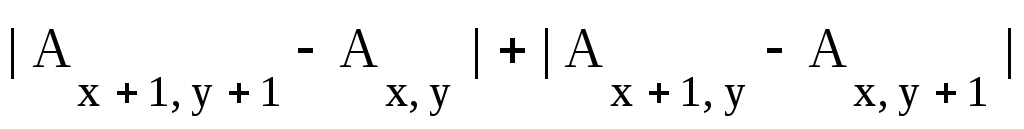 .
.
В алгоритме Собеля используется восемь отсчетов яркости в окрестностях центральной точки:
G(x,
y)
=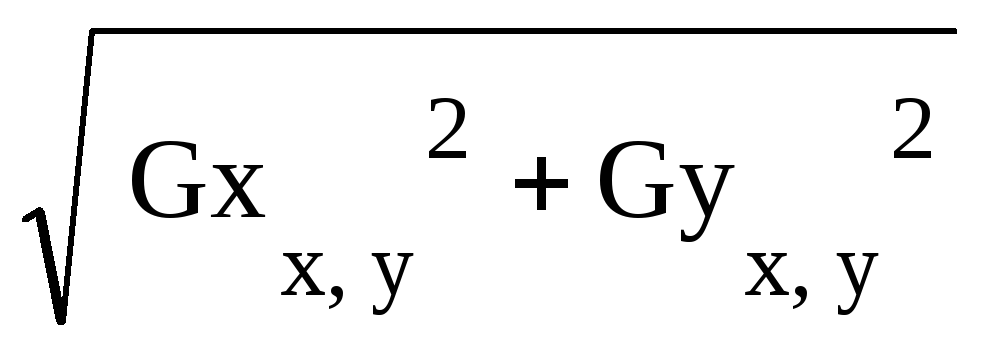 , G(x,
y)
, G(x,
y)
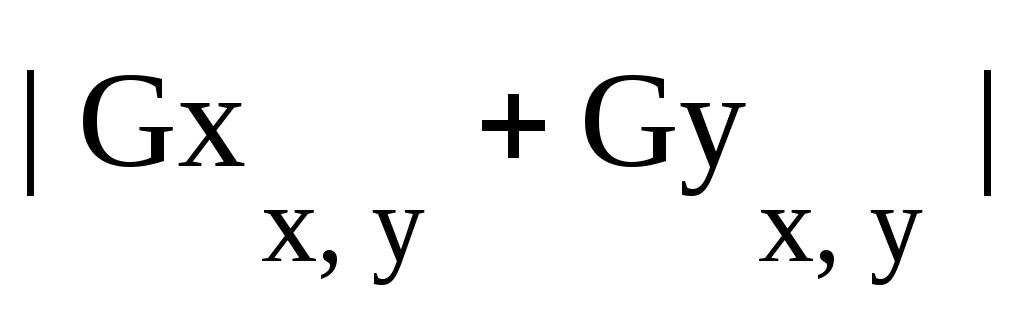 ,
,
Gxx,y= [Ax-1,y-1+2Ax-1,y+Ax-1,y+1] — [Ax+1,y-1+2Ax+1,y+Ax+1,y+1],
Gyx,y = [Ax-1,y-1+2Ax,y-1+Ax+1,y-1] — [Ax-1,y+1+2Ax,y+1+Ax+1,y+1].
Наряду с более точным определением нормы градиента алгоритм Собеля позволяет определять и направление вектора градиента в плоскости анализа изображения в видеугла между вектором градиента и направлением строк матрицы:
(x, y) = argtg(Gyx,y /Gxx,y).
В отличие от сглаживающих и контрастоповышающих фильтров, не меняющих среднюю интенсивность изображения, в результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю. Вертикальным перепадам (границам) исходного изображения соответствуют пиксели с большими по модулю значениями на результирующем изображении. Поэтому разностные фильтры называют также фильтрами выделения границы объектов.
Аналогично вышеприведенным фильтрам, по методу конечных разностей можно составить фильтры для других дифференциальных операторов. В частности, важный для многих приложений дифференциальный оператор Лапласа (лапласиан) = 𝝏2/𝝏x2 + 𝝏2/𝝏y2 можно приблизить для дискретных изображений фильтром с матрицей (один из вариантов):
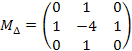 .
.

Рис. 17.3.2.
Как видно на рис. 17.3.2, в результате применения дискретного лапласиана большие по модулю значения соответствуют как вертикальным, так и горизонтальным перепадам яркости. Фильтр является, таким образом, фильтром, находящим границы любой ориентации. Нахождение границ на изображении может производиться путем применения этого фильтра и взятия всех пикселей, модуль значения которых превосходит некоторый порог.Однако такой алгоритм имеет существенные недостатки. Главный из них — неопределенность в выборе величины порога. Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях. Кроме того, разностные фильтры очень чувствительны к шумам изображения.
Двумерная циклическая свертка. Как и для одномерных сигналов, двумерная свертка может выполняться в области пространственных частот с использованием алгоритмов быстрого преобразования Фурье и перемножением двумерных спектров изображения и ядра фильтра. Она также является циклической, и выполняется обычно в скользящем варианте. С учетом цикличности, для вычисления постоянного шаблона спектра ядра размеры маски фильтра ядра удваиваются по осям и дополняются нулями, и эти же размеры маски используются для выделения скользящего по изображению окна, в пределах которого и выполняется БПФ. Реализация КИХ фильтра с помощью БПФ особенно эффективна, если фильтр имеет большую опорную область.
Нелинейные фильтры. В цифровой обработке изображений широко применяются нелинейные алгоритмы на основе ранговой статистики для восстановления изображений, поврежденных различными моделями шумов. Они позволяют избежать дополнительного искажения изображения при удалении шума, а также значительно улучшить результаты работы фильтров на изображениях с высокой степенью зашумленности.
Введем понятие M-окрестности элемента изображения A(x, y), который является для этой окрестности центральным. В простейшем случае M-окрестность содержит N-пикселей – точки, попадающие в маску фильтра, включая (или не включая) центральный. Значения этих N-элементов можно расположит в вариационном ряду V(r), ранжированном по возрастанию (или убыванию), и вычислить определенные моменты этого ряда, например, среднее значение яркости mN и дисперсии dN. Вычисление выходного значения фильтра, которым заменяется центральный отсчет, выполняется по формуле:
B(x, y) = А(x, y) + (1-)mN. (17.3.2)
Значение коэффициента связывается определенной зависимостью со статистикой отсчетов в окне фильтра, например:
dN /(dN + k dS), (17.3.3)
где dS – дисперсия шумов по изображению в целом или по S-окрестности при S > M и MS, k — константа доверия дисперсии S-окрестностей. Как следует из этой формулы, при k=1 и dN dS имеет место 0.5, а значение B(x, y) = (А(x, y) + mN)/2, т.е. складываются в равной степени от значений центрального отсчета и среднего значения пикселей его M-окрестности. При увеличении значений dN происходит увеличение вклада в результат значения центрального отсчета, при уменьшении – значения mN. Весомость вклада средних значений по M-окрестности можно изменять значением коэффициента k.
Выбор статистической функции и характер зависимости от нее коэффициента может быть достаточно многообразным (например, по дисперсиям разностей отсчетов в М-окрестности с центральным отсчетом), и зависит как от размеров апертуры фильтра, так и от характера изображений и шумов. По существу, значение коэффициента должно задавать степень поврежденности центрального отсчета и, соответственно, функцию заимствования для его исправления отсчетов из М-окрестности.
Наиболее простыми и распространенными типами нелинейных фильтров для обработки изображений являются пороговые и медианные фильтры.
Пороговая фильтрация задается, например, следующим образом:
B(x,
y)
= 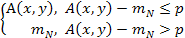
Величина p является порогом фильтрации. Если величина центральной точки фильтра превышает среднее значение отсчетов mN в ее М-окрестности на величину порога, то она заменяется средним значением. Значение порога может быть как константой, так и функционально зависимым от величины центральной точки.
Медианная фильтрация определяется следующим образом:
B(x, y) = med {M(x, y)},
т.е. результат фильтрации есть медианное значение пикселей окрестности, форма которой определяется маской фильтра. Медианная фильтрация способна эффективно удалять из изображения помехи, независимо воздействующие на отдельные пиксели. Например, такими помехами являются «битые» пиксели при цифровой съемке, «снеговой» шум, когда часть пикселей заменяется на пиксели с максимальной интенсивностью, и т.п. Преимущество медианной фильтрации заключается в том, что «горячий» пиксель на темном фоне будет заменен темным, а не «размазан» по окрестности.
Медианная фильтрация обладает выраженной избирательностью по отношению к элементам массива, представляющим собой немонотонную составляющую последовательности чисел в пределах апертуры фильтра. В то же время монотонную составляющую последовательности медианный фильтр оставляет без изменений. Благодаря этой особенности, медианные фильтры при оптимально выбранной апертуре сохраняют без искажений резкие границы объектов, подавляя некоррелированные или слабо коррелированные помехи и малоразмерные детали.
Фильтры экстремумов определяются по правилам:
Bmin(x, y) = min {M(x, y)},
Bmax(x, y) = max {M(x, y)},
т.е. результат фильтрации есть минимальное и максимальное значения пикселей в маске фильтра. Применяются такие фильтры, как правило, для бинарных изображений.
Фильтры
© 2012 Vasili-photo.com
Фотограф использует светофильтры тогда, когда свет не оптимален, а фильтр может его улучшить. Практика показывает, что лучшие снимки делаются без фильтров. Когда освещение идеально, фильтры попросту не нужны. Однако идеальным освещение бывает редко, и если у вас нет возможности дожидаться благоприятных условий, фильтры могут прийти на помощь. Фильтр не сделает плохой свет хорошим, но он может сделать плохой свет приемлемым для съёмки.
Не стоит забывать и о том, что человеческое зрение работает весьма отличным от фотоаппарата образом, поэтому зачастую использовать фильтры приходится просто для того, чтобы сцена вышла на фотографии так, как её видим мы с вами, а не так, как её хочет видеть камера. Именно так – противоестественные манипуляции необходимы для того, чтобы фотографии выглядели естественно. Игнорирование этого принципа ведёт к тому, что большинство любительских снимков смотрятся ненатурально.
При работе с плёнкой фильтры жизненно необходимы. Для цифровой фотографии использование фильтров не столь критично, но ряд фильтров не утратил своей актуальности. Да, некоторые эффекты от использования фильтров могут быть с различной степенью успешности сымитированы в графических редакторах, но, поверьте, обрабатывать хороший кадр, аккуратно экспонированный, снятый с использованием нужных фильтров, значительно легче и приятнее, нежели пытаться вытянуть снимок, небрежно щёлкнутый с пагубной уверенностью во всемогуществе Фотошопа. Сам я, кстати, редко пользуюсь фильтрами. Во-первых, из-за лени, а во вторых, я предпочитаю всячески уклоняться от съёмки, когда свет посредственен и нуждается в чрезмерной модификации. Светофильтры – слабая альтернатива хорошему освещению.
И всё же не лишним будет знать, какие бывают фильтры, и зачем они могут вам понадобиться.
Защитные фильтры
Эти фильтры практически никак не влияют на конечное изображение, но, тем не менее, могут быть весьма полезны.
Производители и продавцы фотоаксессуаров называют защитные фильтры ультрафиолетовыми (УФ или UV), на том основании, что они не пропускают свет с короткой длиной волны и тем самым спасают ваши снимки от ужасного воздействия ультрафиолетового излучения. Не покупайтесь на подобную чушь. Не спорю, вероятно, они не пропускают ультрафиолет, как не пропускает его и обычное оконное стекло. Почему «вероятно»? Да потому, что вы никогда не увидите разницу между снимками, сделанными с УФ фильтром и без оного. Ультрафиолет неразличим для человеческого глаза, как в жизни, так и на цифровых снимках. Плёнка – иной разговор, и отдельные типы фотографических плёнок действительно выигрывают от УФ фильтрации, но к цифровой фотографии это не относится.
Некоторые фильтры промаркированы как цифровые (digital), поскольку якобы оптимизированы для использования с цифровыми камерами. Наивные фотолюбители верят в то, что один кусок прозрачного стекла имеет какие-то волшебные преимущества над другим, точно таким же куском, и готовы платить за фильтр с надписью «digital» в два раза больше, чем за фильтр без подобной надписи.
Единственная функция защитных фильтров – механическая защита. Они защищают переднюю линзу объектива от пыли, царапин, отпечатков пальцев и т.п. Заменить разбитый фильтр выйдет дешевле, чем заменить линзу. Впрочем, если вы уроните объектив на скалы, фильтр его вряд ли спасёт.
Нет ничего плохого в постоянном ношении защитного фильтра на объективе, но ещё лучше научиться обращаться с объективом настолько аккуратно, чтобы необходимость в дополнительной защите не возникала. Кстати, бленда, носимая в рабочем положении, также неплохо предохраняет переднюю линзу и к тому же помогает бороться с бликами.
Вопреки легендам защитный фильтр не ухудшает резкость изображения. Если у вас есть сомнения, проверьте сами, делая серии снимков с фильтром и без. Единственная ситуация, которая чревата незначительной потерей контраста, это съёмка в контровом свете. Но здесь, знаете ли, и без фильтров снимать непросто.
Защитный фильтр должен быть прозрачен. В идеале, когда вы вынимаете его из упаковки, у вас должно возникать впечатление, что производитель забыл вставить стекло в оправу.
Дорогие фильтры с просветлением хороши тем, что меньше бликуют. Вместе с тем даже самые простые и дешёвые фильтры прекрасно справляются со своей защитной функцией.
Нейтральные фильтры
Фотографу всегда не хватает света, но случается и обратное. Например, вы снимаете водопад и хотите получить воду размытой, а скалы резкими. Для этого нужна длинная выдержка, но свет слишком ярок, а ждать наступления сумерек у вас нет никакой возможности. В таких случаях используют нейтрально серые фильтры (ND – Neutral Density), которые представляют собой просто тёмное стекло в оправе, блокирующее часть света, поступающего в объектив, и позволяющее таким образом снимать с малыми скоростями затвора. Нейтральный фильтр не должен иметь цветового оттенка – в идеале он серый – иначе он начинает оказывать влияние не только на экспозицию, но и на цветовой баланс, т.е. перестаёт быть нейтральным.
Нейтральные фильтры бывают разной кратности. Кратность фильтра означает, на сколько ступеней следует увеличить экспозицию при его применении. Например, фильтр ND 8 ослабляет световой поток в 8 раз, т.е. блокирует 3 ступени экспозиции. Некоторые производители указывают не кратность фильтра, а его оптическую плотность, используя логарифмическую шкалу, где каждой ступени экспозиции соответствуют 0,3 единицы. Упомянутый выше восьмикратный фильтр будет обозначен как ND 0,9, а ND 4 превратится в ND 0,6.
Фильтры с высокой кратностью очень сильно затемняют видоискатель, что затрудняет компоновку кадра. Кроме того, при недостатке света ухудшается работа автофокусировки вплоть до полного отказа. Здесь имеет смысл скомпоновать кадр и сфокусировать объектив без фильтра, зафиксировать камеру на штативе, и лишь затем накрутить фильтр и сделать снимок.
Градиентные фильтры
Если у нейтрального фильтра затемнена только половина, а вторая половина прозрачна, причём между двумя зонами имеется плавный переход, такой фильтр называется градиентным (Graduated ND). Он применяется для съёмки высококонтрастных сцен, например закатов, когда небо значительно ярче пейзажа. Затенив с помощью фильтра верхнюю часть кадра, вы получаете возможность увеличить экспозицию в нижней части и таки уместить всю сцену в динамический диапазон камеры.

Снято без фильтра.

Снято с использованием градиентного фильтра.
Наведите курсор, чтобы сравнить с предыдущим кадром.
Градиентные фильтры весьма разнообразны. Тёмная часть фильтра может иметь различную плотность; собственно градиент может быть плавным или же представлять собой чёткую границу, линия которой может быть как прямой, так и изогнутой, чтобы соответствовать рельефу местности. Существуют обратные градиентные фильтры, имеющие тёмную полосу посередине и светлые края. Их используют, чтобы притенить закатное солнце, оставив верх и низ кадра без изменений. Фильтр может быть нейтрально серым, а может – и цветным для придания небу желаемого оттенка.
Большинство градиентных фильтров имеют круглую форму и стандартную оправу с резьбой, но при этом могут поворачиваться внутри оправы, чтобы дать фотографу возможность управлять наклоном градиента. Однако существуют и большие квадратные фильтры, которые вставляются в специальный держатель, предварительно закреплённый на объективе. Такие фильтры могут скользить по направляющим держателя вверх и вниз, позволяя изменять положение границы тёмной и светлой областей фильтра. Сам же держатель может быть повёрнут для обеспечения нужного угла наклона. Лично я предпочитаю круглые фильтры в обычной оправе, поскольку нахожу систему с держателем слишком громоздкой, но это дело вкуса.
Использовать градиентные фильтры следует аккуратно. Остерегайтесь сцен, содержащих предметы, пересекающие границу между тёмной и светлой половинами. Представьте себе горные вершины на фоне затянутого облаками неба. Небо слишком светлое, а горы слишком тёмные. Если вы примените в этой ситуации градиентный фильтр – то да, вам удастся получить детали и в облаках, и у подножия гор, но собственно вершины станут почти чёрными, что будет выглядеть особенно неестественным, учитывая нормально проэкспонированный низ сцены. Вряд ли вы найдёте в продаже фильтр с зубчатой границей, в точности повторяющей рисунок горного хребта.
Идеальный сюжет для применения градиентного фильтра – закат над морем или степью, поскольку граница между зонами с различной яркостью ровная и совпадает с горизонтом.
Градиентные фильтры незаменимы при съёмке на цветную обращаемую плёнку в силу её малого динамического диапазона. При работе с цифровой камерой зачастую можно обойтись и без фильтра, призвав на помощь HDR, т.е. сделав несколько снимков с различной экспозицией, объединить их затем в единое изображение. Метод превосходный, но требует аккуратности и большого вкуса. Кроме того, для HDR непременно нужен штатив и неподвижный сюжет. Если вы снимаете с рук или если в кадре присутствуют раскачиваемые ветром деревья, градиентный фильтр – единственный выход.
Поляризационные фильтры
Это, без сомнения, наиболее интересная группа фильтров.
Прежде всего, разберёмся, что такое поляризация. Световая волна, двигаясь в некоем направлении, совершает колебания в плоскости, проходящей через вектор направления её полёта. Как вы понимаете, через любой вектор, может проходить бесконечное количество плоскостей. Обычный неполяризованный свет, излучаемый каким-либо источником, например солнцем, содержит примерно одинаковое количество световых волн, ориентированных в каждой из бесчисленного множества воображаемых, взаимопересекающихся плоскостей. Если волны света ориентированы неравномерно, т.е. значительная часть волн колеблется в параллельных друг другу плоскостях, такой свет называется поляризованным.
Солнечный свет не поляризован, но он поляризуется, отражаясь от стекла, воды и прочих гладких неметаллических поверхностей, а также, прошу обратить особое внимание, от молекул воздуха.
Поляризационный фильтр (PL, Polarizer) устроен таким образом, что пропускает световые волны только с определённой плоскостью поляризации. Точно так же, как и градиентный фильтр, поляризатор может поворачиваться в оправе, позволяя фотографу выбирать: какие световые волны попадут в объектив, а какие нет.
Поворачивая поляризатор в оправе, можно подобрать положение, при котором он почти полностью блокирует отражённый поляризованный свет. Например, в пасмурную погоду вам не хочется, чтобы вода в лесном озере отражала скучное белесое небо. С помощью поляризационного фильтра вы можете исправить ситуацию, убрав отражение и сделав видимым дно водоёма вместе с камнями и водными растениями, что может очень оживить кадр.
Поляризатор часто используют, чтобы устранить блики на листьях деревьев, а также на мокрых камнях. Это может сделать цвета более насыщенными, но может и убить кадр, лишив сцену объёма, так что знайте меру – не всегда то положение фильтра, при котором его эффект максимален, будет самым уместным положением.

Без фильтра.

С поляризационным фильтром.
Наведите курсор для сравнения.
Наиболее популярное применение поляризационного фильтра – это получение тёмно-синего неба в ясную погоду. Молекулы воздуха, а также частицы пыли, отражая свет, поляризуют его. Это позволяет, отсекая часть поляризованных волн, притемнять небо, оставляя при этом яркость пейзажа неизменной.

Без фильтра.

С поляризационным фильтром.
Свет от неба поляризован неравномерно. Наиболее сильно эффект поляризации выражен если смотреть под прямым углом к солнцу, и практически полностью отсутствует вокруг солнца, а также на противоположном солнцу участке неба. Отсюда два вывода: во-первых, при съёмке с поляризатором наиболее выгодны такие позиции, при которых солнце находится сбоку от вас, а во-вторых, следует быть исключительно внимательным, если вы используете поляризатор вместе с широкоугольным объективом. Если кадр включает в себя большой участок неба, то из-за разной степени поляризации света вы рискуете получить в небе тёмную полосу, выглядящую крайне неестественно, и с головой выдающую вашу неудачную попытку обмануть законы природы.

Пример не слишком удачного применения поляризатора вместе с широкоугольным объективом.
Не забывайте, что поляризационный фильтр крадёт у вас около двух ступеней экспозиции, т.е. при прочих равных условиях заставляет использовать в четыре раза более длинную выдержку. Это означает, что снимать через поляризатор, держа камеру в руках, вы сможете только в солнечную погоду. В тени или же в вечернее время штатив может оказаться отнюдь не бесполезным.
Следует, пожалуй, упомянуть, что поляризационные фильтры бывают линейными и круговыми (C-PL, Circular Polarizer). Не буду вдаваться в технические подробности, но знайте, что автофокус и экспозамер современных камер адекватно работает только с фильтрами, обеспечивающими круговую поляризацию. Беспокоиться по этому поводу не стоит – все поляризаторы, выпускающиеся в XXI веке, круговые, и отыскать неправильный фильтр в настоящее время не так-то просто.
Цветные фильтры
Значимость этих фильтров для фотографа сильно колеблется в зависимости от материала, на который он снимает.
При работе с чёрно-белой плёнкой цветные светофильтры исключительно важны, поскольку, пропуская одни лучи и задерживая другие, позволяют изменять тональные отношения между предметами, а так же управлять контрастом.
При использовании цветных слайдов фильтры необходимы для коррекции цветового баланса плёнки и получения естественных цветов при различном освещении.
Если же ваш основной инструмент – цифровая камера, цветные фильтры вам абсолютно ни к чему. Баланс белого позволяет производить гораздо более смелые манипуляции с цветом, чем любые фильтры. А работа с индивидуальными цветовыми каналами при чёрно-белой конвертации снимков даёт даже больший творческий простор, чем цветные светофильтры в традиционной фотографии.
Эффектные фильтры
К этой категории можно отнести диффузные, звёздные, радужные и прочие подобные фильтры. Художественная ценность таких спецэффектов вызывает у меня глубочайший скептицизм. Более того, большая часть этих фильтров без труда может быть сымитирована в Фотошопе. Если вам угодно побаловаться эффектными фильтрами – вы в своём праве, рассматривать их как серьёзное изобразительное средство мне трудно.
Размеры
Фильтры выпускаются в оправах различного диаметра, и покупать очередной фильтр следует в зависимости от размера передней линзы объектива, для которого этот фильтр предназначен. Большие светосильные объективы требуют соответственно больших фильтров. Существуют переходные кольца, позволяющие использовать фильтры, размер которых не соответствует резьбе на объективе. Маленькие фильтры (скажем, 52 мм) относительно дёшевы и весьма удобны, но, к сожалению не совместимы с крупной оптикой.
Я настоятельно не советую вам брать с собой фильтры разного размера, даже если ваша коллекция включает в себя все возможные и невозможные размеры. Привычка носить в сумке десяток фильтров, которыми приходится непрестанно жонглировать, очень усложняет жизнь и заметно снижает вашу оперативность. Если вы отправляетесь на фотовылазку с несколькими объективами, выбирайте их таким образом, чтобы все они имели одинаковую резьбу для фильтров. Другой вариант – взять комплект фильтров, подходящих к объективу с наибольшей резьбой (например, 77 мм), а остальные объективы снабдить повышающими переходными кольцами.
Некоторые широкоугольные объективы с большой выпуклой передней линзой в принципе не имеют резьбы и не могут быть использованы вместе с традиционными фильтрами. К некоторым объективам специальные тонкие фильтры крепятся сзади. Иногда фильтры не накручиваются на объектив, а вставляются внутрь, в специальную обойму, однако такая конструкция – редкость.
Просветление
Просветление или, как его ещё называют, антибликовое покрытие это тончайшая плёнка, наносимая на оптическое стекло с целью повысить его светопропускающую способность и избавиться от бликов.
Фильтры без просветления блестят так же, как обычное оконное стекло. В нормальных условиях вы не заметите никакого ухудшения качества изображений. Если же в поле зрения объектива попадает солнце или какой-нибудь другой яркий источник света, фильтр без покрытия умножит блики, возникающие из-за переотражения света линзами объектива, а также будет способствовать снижению контраста. Всё это звучит страшно, но на деле деградация картинки не всегда даже заметна для невооружённого глаза. В крайнем случае, несложно завести привычку снимать с объектива защитный фильтр, когда вы снимаете против солнца.
Преимущество непросветлённых фильтров в дешевизне, а также в том, что их легко чистить. В сущности, их спокойно можно мыть под краном или протирать носовым платком (чистым, разумеется!), в то время как фильтры с покрытием требуют более деликатного обращения.
Фильтры с однослойным просветлением можно распознать по маркировке SC или C (Single Coated или же просто Coated), а также по желтоватому или голубоватому оттенку отражений в стекле фильтра. Сами отражения заметно более тусклые, чем в фильтрах без просветления. В контровом свете просветлённые фильтры ведут себя лучше, чем непросветлённые, но опять же, разница незначительна, и отнюдь не поражает воображение.
Самые лучшие и, как следствие, дорогие фильтры имеют многослойное просветление, которое ещё более эффективно борется с бликами и доводит светопропускание фильтра почти до 100%. Такие фильтры на вид абсолютно прозрачны, и даже яркие объекты отражаются в них очень тускло с зеленовато-пурпурным отливом. Маркировка может быть самая различная: MC (Multi Coated), SMC (Super Multi Coated) и т.п.
А вот, собственно, за что мы платим:

Без фильтра.

Фильтр с многослойным просветлением.

Обычный фильтр.
Да уж, разница не впечатляет. При этом мне пришлось приложить немало усилий, чтобы добиться столь ужасных бликов. Никто в здравом уме не станет снимать в таких условиях.
Если коротко, то многослойное покрытие лучше, чем однослойное, которое в свою очередь лучше, чем вообще никакого покрытия. При этом даже фильтр с многослойным покрытием всё равно будет бликовать при встречном свете, хоть и незначительно. В любом случае, независимо от наличия просветления и его типа, различия в качестве изображения несущественны, и проявляются лишь при экстремальном освещении.
Чистить просветлённые фильтры следует аккуратно, чтобы не поцарапать покрытие. Хорошо зарекомендовали себя салфетки из микроволокна или микрофибры. Впрочем, небольшое количество пыли на фильтре или объективе вполне допустимо и совершенно не влияет на ваши снимки.
Рекомендации
Цифровому фотографу нет нужды запасаться фильтрами всех цветов радуги, но я советую вам обзавестись поляризационным и градиентным фильтрами. Размеры подбирайте исходя из того, с какими объективами вы будете эти фильтры использовать. Если у вас много объективов с разной резьбой, старайтесь по возможности приобретать фильтры большего диаметра и решать проблему совместимости с помощью набора повышающих переходных колец.
Имейте в виду, что у некоторых недорогих объективов передняя линза вращается при фокусировке. Это чрезвычайно затрудняет использование фильтров во вращающейся оправе вместе с подобными объективами.
Помимо двух вышеупомянутых фильтров нелишним будет обзавестись защитными или ультрафиолетовыми фильтрами для каждого из ваших объективов. Даже если вы и не будете носить их постоянно, защитные фильтры могут вам понадобиться при съёмке в суровых условиях, когда велик риск попадания в объектив снега, песка, водных брызг и прочих малоприятных вещей.
Если вы носите на объективе защитный фильтр, не забывайте снимать его, прежде чем накрутить на объектив поляризатор или градиентный фильтр. Иными словами: не стоит готовить бутерброды из фильтров. Чем больше слоёв стекла вы помещаете перед объективом, тем сильнее вы рискуете поймать лишние блики, не говоря уже о потере общей светопропускающей способности всей системы.
Из производителей я могу порекомендовать Marumi за хороший баланс цены и качества. Hoya несколько лучше, но дороже. Поляризаторы Hoya и Marumi одни из лучших, а многослойное просветление фильтров Hoya и вовсе вне конкуренции.
B+W делает выдающиеся фильтры с не менее выдающейся ценой.
Очень популярны градиентные фильтры Cokin, особенно среди любителей квадратных фильтров. Cokin выпускает градиентные фильтры всех мыслимых и немыслимых цветов, но, к сожалению без намёка на просветление. К тому же все они пластиковые, а не стеклянные.
Неплохие нейтрально-серые градиентные фильтры в традиционной оправе делает Tiffen. Особенно хороши фильтры серии HT с многослойным покрытием.
Градиентные фильтры производства Hoya и B+W сделаны из пластика и могут быть не вполне нейтральны по цвету.
Про фильтры Kenko я не могу сказать ничего плохого.
Кроме того многие производители фототехники такие как Nikon, Canon, Fuji и пр. также выпускают фильтры под собственными брендами.
Если вам нужен защитный фильтр без просветления, который не жалко поцарапать или даже разбить, знайте, что дешёвые китайские фильтры работают ничуть не хуже дорогих фирменных фильтров. Перед тем как использовать безымянный фильтр убедитесь в том, что он безупречно прозрачен, и что его оправа достаточно тонкая, чтобы не вызывать виньетирование.
Спасибо за внимание!
Василий А.
Post scriptum
Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.
Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.
Желаю удачи!
| Дата публикации: 19.09.2012 |  |
Вернуться к разделу «Специальные приёмы»
Перейти к полному списку статей
Размытие изображения фильтром Kuwahara / Habr
Фильтр Kuwahara выполняет нелинейную фильтрацию изображений с сохранением резких краев. После фильтрации изображение похоже на грубо нарисованную красками, картину.Алгоритм
- В окрестности каждого пикселя применить маску размером (2r+1)*(2r+1)
- Окрестность разделить на 4 области, указанные цифрами I, II, III, IV, размером r*r
- Вычислить среднюю интенсивность и дисперсию в каждой из областей I, II, III, IV
- Присвоить центральному пикселю X среднее значение интенсивности той области, дисперсия которой наименьшая
Маска фильтра
Применение
Сегментация однородных по цвету областей
Допустим у нас стоит задача поиска водоемов на космоснимке. На этапе предварительной обработке необходимо очистить изображение от шумов и сделать его более гладким и однородным. Причем должна быть сохранена информация о границах объектов в изображении. Применяем к исходному изображению фильтр kuwahara.
Исходное изображение
Kuwahara 21×21
После фильтрации границы стали более четкими, и к изображению можно применить какой-нибудь контурный фильтр, например детектор Канни.
Детектор Канни, примененный после фильтрации kuwahara
Для сравнения, если бы мы в качестве предварительной обработке использовали бы фильтр Гаусса, получили бы следующие изображения:
Фильтр Гаусса 21×21
Применение фильтра для создания эффекта нарисованной картины
Хоть это и не самый лучший фильтр для создания эффекта акварели или гуаши, но во многих случаях, на мой взгляд, получается очень даже красивый эффект.
Исходное изображение
Kuwahara 21×21
