Code Gris серый 60×60 Керамогранит Laparet, Россия
Частые вопросы
1Насколько большой выбор в вашем магазине?
Найдите ту плитку, которая нужна именно Вам! Мы поддерживаем огромный ассортимент, что бы ни терять, ни одного своего посетителя и каждому предложить то, что ему нравится. Любую плитку можно подобрать с помощью удоного фильтра в каталоге.
2Как срочно, вы можете доставить плитку?
Как правило, при заказе плитки до обеда вы сможете получить ее уже на следующий день. Минимальный срок доставки в нашем магазине 1 день. Не заставляйте себя ждать, закажите плитку и получите ее в кратчайшие сроки!
3Есть ли у вас недорогая плитка?
С точки зрения заработка, нам гораздо удобнее всегда продавать дорогую итальянскую плитку, но мы понимаем, что далеко не все покупатели могут позволить себе такую покупку. Поэтому в нашем ассортименте всегда широкий выбор плитки отечественных фабрик и производителей из ближнего зарубежья, чья продукция отличается невысокой ценой.
4Я не смог дозвониться, вы перезвоните?
Нас, так же как и вас, очень раздражает, когда нам не перезванивают менеджеры интернет-магазинов. Поэтому мы перезваниваем всегда, включая те случаи, когда понимаем, что товара нет в наличии и продажу мы совершить не сможем. Звоните нам или заказывайте на сайте и будьте уверены, мы Вам перезвоним!
5Нужно ли вносить предоплату?
Оплачивайте при доставке, не выходя из дома. Для вашего удобства мы предусмотрели возможность оплаты при доставке, поэтому нет никакой необходимости приезжать к нам заранее и вносить предоплату за покупку. Подробнее…
6Можно ли купить плитку не выходя из дома с оплатой при получении?
Благодаря удобной системе заказа плитки, Вы можете получить ее, не выходя из дома. Совершая покупки онлайн круглосуточно, Вам останется только принять плитку от нашего водителя-экспедитора. Оплата производится по факту получения плитки.
7У вас есть дисконтные карты?
В магазине BestCeramic.ru действует система скидок по дисконтным картам, которую Вы обязательно получите при покупке. Условия подробно…
8Вам не хватило? Мы довезем!
Самая распространенная ошибка при покупке плитки это неправильный расчет, когда ее попросту не хватает. А для магазина продавать одну-две плитки совершенно неудобно и не выгодно и далеко не все магазины это делают. Совершая у нас заказ, вы можете рассчитывать на то, что мы впоследствии вас не бросим и привезем недостающую вам плитку. Покупайте, не думая об ошибках, мы всегда поможем их исправить. Условия доставки Подробнее…
9Я не уверен сколько нужно плитки, поможете рассчитать?
Самой распространенной ошибкой при приобретении плитки является то, что покупатель не рассчитывает запас плитки на случаи подрезки или боя и приобретение недостающей является большой проблемой! Наши менеджеры-консультанты всегда помогут правильно рассчитать кол-во плитки, с учетом необходимого запаса на бой и подрезку при укладке.
10Можно ли вернуть товар?
Если Вы хотите вернуть плитку, сделать это можно в течение 2-х недель с момента покупки. И хоть плитка и является товаром, отпускаемым на метры, а в законе о правах потребителя четко сказано, что такой товар возврату и обмену не подлежит. Мы всегда, без проблем, принимаем возврат, если нам сдают его полностью в том объеме, в котором мы его продали.
Кресло складное мягкое ECONOMY с высокой спинкой, цвет серый/темно-серый Код товара: 1040663
1 отзыв
- Описание товара
- Характеристики и видеообзоры
- Сопутствующие товары 56
- Отзывы 1
Код товара: 1040663
- Серый/Темно-серый
- Белый/Синий
- Серый/Синий
- Серый/Красный
- Белый
- Камуфляж
В наличии
12 073 ₽
| Материал обивки | Пластик/Ткань |
| Все характеристики | |
Характеристики | |
| Цвет | Серый/Темно-серый |
|---|---|
| Ширина спинки | 400 мм |
| Ширина общая | 410 мм |
| Высота общая | 570 мм |
| Высота спинки | 420 мм |
| Глубина | 360 мм |
| Крепежные размеры | 5″ х 5″ |
| Габариты | 570х360х380 мм |
| Вес | 4,07 кг |
| Материал обивки | Пластик/Ткань |
| Производитель | Springfield |
| Страна производителя | США |
| Страна производства | Китай |
Складные кресла Economy и Skipper
23 апр 2014
Остановить и закрыть
{raw title}
{date}
Описание
 Компактное и удобное, для комфортного отдыха на воде.
Компактное и удобное, для комфортного отдыха на воде.
НК
Николай Кондратенко
4
Достоинства
Купил поставил в лодку надувную и доволен. Спину держит. Пятая точка не бьется об лавку. Рыбалка намного комфортнее, особенно когда бросил якорь и сидишь поплавок караулишь.
Комментарий
Все норм, но доставляли дольше чем написано на сайте, что-то пошло не так. В итоге довезли.
Код Грея в учебнике по цифровой электронике
следующий → ← предыдущая Код Грея представляет собой последовательность двоичных систем счисления, которая также известна как , отраженный двоичный код . Код Грея является очень легким взвешенным кодом, поскольку он не зависит от значения цифры, определяемой позицией. Этот код также называется циклическим переменным кодом, поскольку переход одного значения в его последующее значение приводит к изменению только одного бита. Как сгенерировать код Грея?Префикс и метод отражения рекурсивно используются для генерации кода Грея числа. Для генерации кода Грея:
Процесс генерации кода ГреяКодовая таблица Грея
Следующая темаExcess-3 Code ← предыдущая следующий → |
Для видео Присоединяйтесь к нашему каналу Youtube: Присоединяйтесь сейчас
Обратная связь
- Отправьте свой отзыв на [email protected]
Помогите другим, пожалуйста, поделитесь
Узнайте последние уроки
Подготовка
Современные технологии
Б.
 Тех / МСА
Тех / МСА Код Грея
Цифровые компьютеры на фундаментальном уровне работают в двоичном формате. Напряжения на проводах есть, либо их нет. Мы называем это base-2 или двоичным , потому что есть только два состояния, в которых может находиться любой элемент. Традиционно, когда мы считаем в двоичном формате, мы имитируем способ счета в других системах счисления, таких как десятичная, с наименее значащими цифрами справа и старшими слева. |
В традиционной двоичной системе счисления каждая -значная -я позиция, которую мы перемещаем влево, является новой степенью этого основания. Это упрощает сравнение чисел, их сложение и выполнение других логических операций, потому что столбцы имеют определенное значение и схожие свойства, связанные с тем, что одна и та же цифра находится в одной и той же позиции. Этому последовательному обозначению разряда присвоено имя позиционное обозначение . |
В любой системе счисления существует множество способов кодирования чисел. Мы могли бы сделать это даже произвольным образом, если бы захотели! Пока каждый шаблон закодированного числа различен, а кодирование повторяемо, его можно использовать для записи числового значения. (Также полезно, если схема кодирования предсказуема и поддается описанию, поэтому нам не нужна таблица декодирования/поиска для интерпретации). Одна из альтернативных систем двоичного* кодирования называется Код Грея (также известный как отраженный двоичный код ) в честь физика Фрэнка Грея. У него много интересных свойств. Но тут мы немного забегаем вперед, давайте вернемся к истокам… |
*Коды Грея можно создавать и с использованием других баз, как мы увидим позже.
Двоичный
Системы на основе двоичных файлов просты и легки в построении. Как упоминалось выше, в компьютерах используются комбинации логических элементов, в которых наличие или отсутствие напряжения указывает на состояние любого бита. Двоичные сигналы однозначны; значение либо установлено, либо нет. Понятия «половинка» не существует. Невосприимчивость к шуму является большим преимуществом. Однако, несмотря на то, что нет никакой двусмысленности в отношении того, на что может быть установлен любой отдельный бит (он должен быть квантован до одного из двух значений), существует вероятность (когда параллельно подключено более одного бита), что не все биты меняют состояние в одно и то же время. В качестве примера посмотрите на двоичную последовательность слева, которая показывает двоичное представление десятичных чисел 0-7. Красным мы видим число 3 , представленное как 011 2 . (нижний индекс 2 используется для обозначения базы счисления, чтобы избежать путаницы с десятичной). Каждое значение изменяется либо с 1 на 0, либо с 0 на 1. Если бы все эти биты мгновенно и синхронно менялись из одного состояния в другое, не было бы никаких проблем, но вне теории этого никогда не бывает! В реальном мире одни биты перевернутся раньше других. Поскольку в этом примере изменяется каждый бит, в зависимости от порядка их изменения и в зависимости от того, когда вы читаете их состояние, может быть возможно прочитать любое значение из этого набора битов!! Такая проблема называется перекос . Микропроцессоры решают эту проблему, имея часы. Часы похожи на метроном и бьют с регулярным ритмом. Битам разрешено изменять состояние, занимая свое собственное время, как они это делают, но считываются только тогда, когда часы бьют в следующий раз. |
Код Грея
Это идеальный переход к Коду Грея. Код Грея— это альтернативное двоичное представление, искусно разработанное таким образом, что между любыми двумя соседними числами изменяется только один бит за раз. Если есть ошибка при чтении какого-либо бита, который изменился тогда, или хуже , считанное значение никогда не будет отставать более чем на одну единицу. |
Это имеет огромное значение в реальном мире. Компьютеры могут быть цифровыми, но мы живем в аналоговом мире. Интерфейсы между ними должны быть тщательно рассмотрены.
Посмотрите на этот вымышленный пример ниже. Вот изображение движущегося ремня, положение которого мы хотим, чтобы компьютер знал с определенной степенью детализации.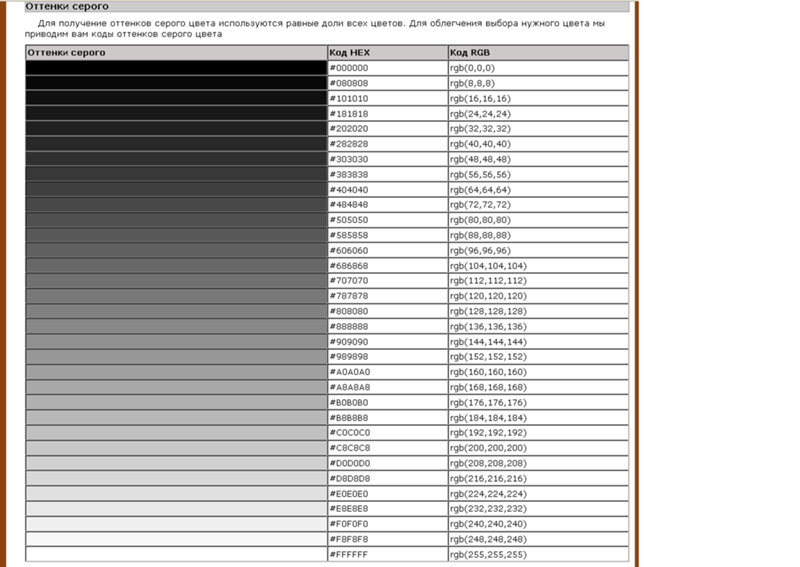 Если бы мы нарисовали символы на ленте, используя двоичный код (тщательно выбирая ширину нарисованных символов и количество битов для разрешения и точности, которые мы хотим измерить), в идеальном мире не было бы никаких проблем.
Если бы мы нарисовали символы на ленте, используя двоичный код (тщательно выбирая ширину нарисованных символов и количество битов для разрешения и точности, которые мы хотим измерить), в идеальном мире не было бы никаких проблем.
Однако, если вы посмотрите на схему, то увидите, что сенсорная полоса не идеально выровнена, и некоторые биты, вероятно, перевернутся раньше других (и даже если полоска была идеально выровнена, в действительности каждый датчик не собирается переворачиваться точно в одно и то же время, так что возникнут сомнения относительно прочитанного значения).
Это может привести к «мусорным» показаниям, и эти фиктивные показания могут быть приравнены к положениям, далеким от истинного положения. Если некоторые биты изменяют состояние раньше других, и вы читаете в этом смешанном состоянии, вы получите ответ, который не является ни первым, ни вторым ожидаемым результатом.
| Слева мы видим три столбца данных. В середине десятичное значение. Слева — позиционная двоичная запись (ванильная двоичная запись, которую мы знаем и любим), а справа — код Грея (отраженная двоичная запись). Вы заметите, что справа каждая соседняя строка отличается от своих соседей не более чем на один бит. Если бы эти коды были пропущены через какой-то аналого-цифровой процесс преобразования (например, пояс выше), либо правильный ответ, либо ответ, находящийся всего в одной единице от правильного ответа, был бы получен при любом чтении. Конечно, это не просто линейные преобразования, вот пример применения трехбитного энкодера вращения вала.
Этот датчик можно использовать для определения ориентации вала с шагом 45°, используя всего три датчика. |
Красивые картинки
Вот диаграмма, показывающая 128 двоичных значений (7 бит) в диапазоне от 0000000 2 слева до 1111111 2 справа. Это красивая картинка, и, как вы понимаете, она рекурсивно самоподобна. Красные пиксели отображают установленный бит.
Это красивая картинка, и, как вы понимаете, она рекурсивно самоподобна. Красные пиксели отображают установленный бит.
Ниже приведен аналогичный график, но на этот раз с кодом Грея. Это интересный паттерн:
Тонкое, но довольно очевидное наблюдение состоит в том, что в коде Грея нет бита, который бы напрямую включал/выключал в двух соседних шагах. Нижняя строка имеет биты, которые включаются/выключаются для двух временных сегментов, а не для одного cf. бинарная версия, которая чередуется. Если бы это было не так, то мы бы не смогли пройти через числа, изменяя только один бит за раз. Бит в нижней строке изменяется, он удерживается там, в то время как другой бит изменяется на следующем шаге, затем его можно переключить обратно …
В следующей строке бит включается/выключается на четыре временных интервала за раз, затем в следующей строке вверх на восемь …
Все дело в базе
Можно создавать коды Грея для более высоких систем счисления (без проблем). Существует несколько способов генерировать коды Грея для получения решений, которые не нуждаются в отражательной балансировке. Некоторые из них имеют интересные характеристики. До сих пор все коды, которые мы описали, были циклическими по своей природе; последовательно оборачиваясь от конца к началу. Можно генерировать коды Грея и без этого ограничения (хотя, честно говоря, я не понимаю его значения, поскольку ступенчатое изменение деформации вокруг вызовет именно ту проблему, которую мы пытаемся решить!)
| 000 → 000 001 → 001 002 → 002 010 → 012 011 → 010 012 → 011 020 → 021 021 → 022 022 → 020 100 → 120 101 → 121 102 → 122 110 → 102 111 → 100 112 → 101 120 → 111 121 → 112 122 → 110 200 → 210 201 → 211 202 → 212 210 → 222 211 → 220 212 → 221 220 → 201 221 → 202 222 → 200 |
Код баланса Грея
Другой подкласс кодов Грея описывается как Сбалансированные коды Грея . Возьмите этот пример слева для 4-битного кода. Как и во всех кодах Грея, каждая строка отличается от строк выше и ниже всего одним изменением цифры. Однако у этого кода есть интересное свойство: каждый бит меняет состояние ровно четыре раза. Он равномерно сбалансирован. Зеленые квадраты показывают место, где меняется состояние каждого бита. Это свойство имеет преимущества в физическом мире. Представьте, например, что вместо световых датчиков в нашем примере с лентой выше машина использовала физические переключатели для каждого из битов для передачи состояния. Если бы использовался ванильный отражающий двоичный код Грея, некоторые переключатели использовались бы значительно чаще и изнашивались бы, чем другие. Поскольку физические коммутаторы имеют ограниченный срок службы, наиболее вероятно, что наиболее часто используемые коммутаторы выйдут из строя первыми. |

 Причиной вызова этого кода как отраженного двоичного кода является сравнение первых N/2 значений с последними N/2 значениями в обратном порядке. В этом коде два последовательных значения отличаются одним битом двоичной цифры. Коды Грея используются в общей последовательности двоичных чисел, генерируемых аппаратным обеспечением. Эти числа вызывают двусмысленность или ошибки при переходе от одного числа к следующему. Этот код просто решает эту проблему, изменяя только один бит, когда выполняется переход между числами.
Причиной вызова этого кода как отраженного двоичного кода является сравнение первых N/2 значений с последними N/2 значениями в обратном порядке. В этом коде два последовательных значения отличаются одним битом двоичной цифры. Коды Грея используются в общей последовательности двоичных чисел, генерируемых аппаратным обеспечением. Эти числа вызывают двусмысленность или ошибки при переходе от одного числа к следующему. Этот код просто решает эту проблему, изменяя только один бит, когда выполняется переход между числами.
 Хорошо известным примером кодирования чисел, в котором , а не , используется позиционная запись, являются римские цифры. Древние римляне, должно быть, обладали терпением святых, чтобы выполнять арифметические действия, используя свои обозначения!
Хорошо известным примером кодирования чисел, в котором , а не , используется позиционная запись, являются римские цифры. Древние римляне, должно быть, обладали терпением святых, чтобы выполнять арифметические действия, используя свои обозначения! При изменении на 4 каждый бит меняет состояние на 100 2
При изменении на 4 каждый бит меняет состояние на 100 2  Тактовая частота выбирается таким образом, чтобы у каждого бита было достаточно времени, чтобы изменить состояние, установиться, а затем быть прочитанным воспроизводимым и согласованным образом.
Тактовая частота выбирается таким образом, чтобы у каждого бита было достаточно времени, чтобы изменить состояние, установиться, а затем быть прочитанным воспроизводимым и согласованным образом. Это представления одних и тех же чисел 0-31 по-разному.
Это представления одних и тех же чисел 0-31 по-разному. Справа пример кода Грея на основе троичных (с основанием 3). Как и в случае с двоичным кодом Грея, каждая строка отличается от обеих сторон заменой всего одной цифры. Кроме того, цифра, которая изменяется, изменяется только на одну единицу.
Справа пример кода Грея на основе троичных (с основанием 3). Как и в случае с двоичным кодом Грея, каждая строка отличается от обеих сторон заменой всего одной цифры. Кроме того, цифра, которая изменяется, изменяется только на одну единицу. У них есть интересное свойство, заключающееся в том, что на бит приходится 90 213 одинаковых переходов состояний.
У них есть интересное свойство, заключающееся в том, что на бит приходится 90 213 одинаковых переходов состояний. 