Амперсанд — Википедия
Материал из Википедии — свободной энциклопедии
 | Статья или раздел содержит противоречия и не может быть понята однозначно. Следует разрешить эти противоречия, используя более точные авторитетные источники или корректнее их цитируя. На странице обсуждения должны быть подробности. |
| Амперсанд | |
|---|---|
| & | |
Изображение
| |
| ampersand | |
| Юникод | U+0026 |
| HTML-код | |
| UTF-16 | 0x26 |
| %26 | |
| Мнемоника | & |
Амперса́нд (&, иногда — амперсе́нд; англ. ampersand) — логограмма, заменяющая союз «и». Возник как лигатура буквосочетания et (с лат. — «и»).
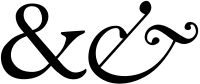Амперсанд прямого и курсивного начертанийАмперсанд является графическим сокращением (лигатурой) латинского союза et («и») — это хорошо видно на изображении амперсанда в курсивном начертании.
В «Кратких сведениях по типографскому делу» называется «знаком, заменяющим союз „и“», в «Справочнике технолога-полиграфиста» — «знаком конъюнкции», в «Справочной книге корректора и редактора» (1974) — «специальным компанейским знаком, разновидностью лигатуры»[источник не указан 3143 дня ][1].
Амперсанд со второй половины VIII века активно используется переписчиками, а с середины XV века — типографами.
Амперсанд стал настолько привычной частью письма в Европе и Северной Америке, что встал на последнее место в английском алфавите во всех букварях уже к началу XIX века (а пропадать из них стал только к началу XX века)[источник не указан 88 дней].
При произношении английского алфавита (например, при заучивании его в англоязычных школах) перед названиями букв, совпадавших с однобуквенными словами, произносили per se (с лат. — «сама по себе», «как таковая») для того, чтобы отличить букву от совпадающего с ней слова. Данная практика также использовалась при произношении слов по буквам: говорилось «I, per se I», чтобы не путать букву с английским местоимением «I» (то есть «я»). Последним знаком в алфавите шёл «&», и заканчивали произношение алфавита словами: «X, Y, Z, and per se and» («„экс“, „уай“, „зед“ и сама по себе „и“», «„и“ как таковая»).
В русском языке[править | править код]
Союз «и» сам по себе короткий, и сокращение ему не нужно. Поэтому в СССР амперсанд ограниченно применялся в научно-технической документации для обозначения логической операции «и» (например, для логических элементов «И» в электрических схемах).
В информатике[править | править код]
Амперсанд в программном обеспечении:
В макроязыке Ассемблера ЕС ЭВМ амперсанд служит признаком параметра.
- В Microsoft Excel символ «&» используется как оператор сцепки текстовых значений.
- В языках Си, С++, Java, C#, JavaScript и других символ «&» применяется для обозначения нескольких операторов:
- для получения ссылки на переменную, унарный оператор, «&» должен предшествовать префиксом идентификатору (имени) переменной;
- оператор «&» обозначает побитовое «И»;
- оператор «&&» обозначает условное логическое И (проверка истинности последующего выражения только при условии истинности предшествующего).
- В GET (системе кодирования запросов HTTP) оператором «&» разделяются аргументы в строке запроса.
- В Бейсике символ &, стоящий сразу после имени переменной, означает тип переменной «длинное целое», а сочетание символов &H означает, что число записано в шестнадцатеричной системе счисления, а в Visual Basic, кроме того, с помощью операции & происходит конкатенация (объединение) строк.
- В SGML (в том числе HTML, XML) конструкция
&name;выводит символ по его названию. Её подвид&#xxxx;(где xxxx — число) выводит символ с кодом xxxx из юникод-пространства. - В большинстве командных интерпретаторов unix-подобных ОС команда, завершённая амперсандом, будет выполняться в «фоновом режиме».
Юникод содержит несколько вариантов амперсанда:
| Графема | Название | Юникод | HTML |
|---|---|---|---|
| & | AMPERSAND | U+0026 | & или & |
| ⅋ | TURNED AMPERSAND | U+214B | ⅋ |
| ﹠ | SMALL AMPERSAND | U+FE60 | ﹠ |
| ＆ | FULLWIDTH AMPERSAND | U+FF06 | ＆ |
| 🙰 | SCRIPT LIGATURE ET ORNAMENT | U+1F670 | 🙰 |
| 🙱 | HEAVY SCRIPT LIGATURE ET ORNAMENT | U+1F671 | 🙱 |
| 🙲 | LIGATURE OPEN ET ORNAMENT | U+1F672 | 🙲 |
| 🙳 | HEAVY LIGATURE OPEN ET ORNAMENT | U+1F673 | 🙳 |
| 🙴 | HEAVY AMPERSAND ORNAMENT | U+1F674 | 🙴 |
| 🙵 | SWASH AMPERSAND ORNAMENT | U+1F675 | 🙵 |
- Коломнин П. П. Краткие сведения по типографскому делу. СПб., 1899. 604 стр.
- Иванова О. Е., Лопатин В. В., Нечаева И. В. и др. Русский орфографический словарь: Около 180 тыс. слов / под ред. Лопатина В. В. 2-е изд., испр. и доп. М.: Изд-во Ин-т рус. яз. им. В. В. Виноградова, 2005. 960 стр. ISBN 5-88744-052-X.
- Справочник технолога-полиграфиста. Ч. 1. Наборные процессы / Сост. Шульмейстер М. В., Таль Г. А. М.: Книга, 1981. 255 стр.
- ГОСТ 2.743-91. Единая система конструкторской документации. Обозначения условные графические в схемах. Элементы цифровой техники
- Allan Haley. Ampersand (англ.). fonts.com
Знак градуса — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Градус. Символы со сходным начертанием: ◌̊ · ゜Знак градуса (°) — типографский символ, используемый для обозначения размерности угла и температуры, а также уменьшённого трезвучия.
По правилам типографского набора знак градуса ставится сразу после числового обозначения величины размерности угла или температуры без всякого пробела, однако если в случае с температурой указывается также шкала, по которой производится измерение (по Цельсию, по Фаренгейту и т. п.), знак градуса отбивается от числовой величины неразрывным пробелом (более точно, используется третная шпация), а символ шкалы следует непосредственно за знаком градуса без пробелов. Ср.:
В первом отсеке камеры должна поддерживаться температура +26 °C, во втором — на 2° холоднее.
В указанное время ракета находилась над Южной Америкой, над точкой земной поверхности с координатами 7° 33′ ю. ш. и 40° з. д.
В Юникоде для совместимости с кодировками CJK китайской письменности, где такие символы присутствуют, поддерживаются совмещённые символы «градус Цельсия» (U+2103 ℃ ) и «градус Фаренгейта» (U+2109 ℉ ), которые вне китайских шрифтов (fullwidth form) не используются.
Следует заметить, что единица температуры в шкале Кельвина называется не «градус Кельвина», а просто «кельвин», поэтому при её использовании знак градуса вообще не ставится. Пример: 273,15 K, где K без знака градуса.
- Unicode: U+00B0.
- HTML:
°. - На компьютерах с операционной системой Windows знак градуса можно вставить, нажав
- На компьютерах с ОС Linux знак можно получить, набрав Composeoo или ⇧ Shift+Ctrl+U и набрав b0↵ Enter после u.
- На компьютерах с Mac OS знак градуса можно вставить, нажав ⌥+0.
- В LaTeX для знака градуса используются команды
\degreeи\textdegreeпредоставляемые пакетами gensymb и textcomp соответственно. Часто этот знак имитируется^\circв математическом режиме.
 | |
|---|---|
| |
Знак — Википедия
Материал из Википедии — свободной энциклопедии
Знак — это материально выраженная замена предметов, явлений, понятий в процессе обмена информацией в коллективе.
Знак — соглашение (явное или неявное) о приписывании чему-либо какого-либо определённого смысла, значения.
Знаком также называют конкретный случай использования такого соглашения для передачи информации. Знак может быть составным, то есть состоять из нескольких других знаков.
Цифры являются знаками чисел. Буквы являются знаками звуков и, вместе со словами, являются знаками человеческого языка.[прояснить]
Ю. М. Лотман утверждает, что знаки делятся на две группы: условные и изобразительные[1].
- Условный — знак, в котором связь между выражением и содержанием внутренне не мотивирована. Самый распространённый условный знак — слово[1].
- Изобразительный или иконический — знак, в котором значение имеет естественно ему присущее выражение. Самый распространённый изобразительный знак — рисунок[1].
Наука о знаковых системах называется семиотикой. Явление возникновения знаковой реальности называется семиотизацией.
Семантический треугольник.Знаком называется материальный объект, который для некоторого интерпретатора выступает в качестве представителя какого-то другого предмета.
- Значение знака (экстенсионал) — предмет, представляемый (репрезентируемый) данным знаком.
- Смысл знака (интенсионал) — информация о репрезентируемом предмете, которую содержит сам знак или которая связывается с этим знаком в процессе общения или познания.
Взаимосвязь этих характеристик можно графически представить в виде семантического треугольника.
- в юриспруденции
В Российской империи при Александре II были утверждены знаки для судебного ведомства, в том числе и для адвокатов.
- в военном деле
- в полиграфии
Используются в правилах дорожного движения
Иероглифы
На основе деления знаков на условные и изобразительные, можно выделить две разновидности искусств: изобразительные и словесные.[1]
Одной из парадоксальных тенденций изобразительного искусства является его тяготение к повествованию, свойственному словесным искусствам[1].
В литературе[править | править код]
Литература — словесное искусство, стремящееся из материала условных знаков создать словесный образ, имеющий явную иконическую природу и являющийся знаком изобразительным.[1]
В дизайне[править | править код]
Знак в дизайне — изобразительная часть логотипа, как правило, включающего также название (письменную — буквенную или иероглифическую — часть, часто также художественно оформленную) маркируемого товара, услуги, организации, мероприятия или персоны. Знак призван закрепить у адресата ассоциацию с маркируемым объектом или его владельцем и служит для различения однотипных объектов в информационном поле адресата (например, на рынке соответствующих товаров). Вместе с именем и логотипом знак составляет основу фирменного стиля (ID, идентичности, айдентики) маркируемого объекта.
Будучи зарегистрирован в патентном ведомстве, знак или логотип получает статус изобразительного или комбинированного товарного знака (знака обслуживания). В этом случае знак может быть снабжён предупредительной маркировкой — индексом ® (registered). Знак, находящийся в процессе регистрации, может быть маркирован индексом ™ (trade mark, торговая марка).
Циркумфлекс — Википедия
Материал из Википедии — свободной энциклопедии
Символы со сходным начертанием: ^ · ◌̑ · へ · ヘ Сюда перенаправляются запросы «Ŵ», «Ŷ», «Ẑ». На эти темы нужны отдельные статьи.| Комбинируемый циркумфлекс | |
|---|---|
| ◌̂ | |
Изображение
| |
| combining circumflex accent | |
| Юникод | U+0302 |
| HTML-код | |
| UTF-16 | 0x302 |
| %CC%82 | |
Циркумфле́кс (лат. circumflexus, «изогнутый вокруг», часто называют «домиком» или «крышечкой») — диакритический знак и компьютерный символ.
В диакритике[править | править код]
- Во французском языке (сирконфлекс) ставится над гласной и обозначает некогда произносившийся, но впоследствии выпавший согласный звук (обычно «s»), долгое время обозначавшийся «немой» буквой: tête < teste. Обозначает открытое «е» [ε].
- В португальском языке ставится над гласными â, ê, ô и обозначает их закрытое произношение под ударением, например, в слове você, а также для различия омонимов (глагола pôr от предлога por).
- В турецком языке факультативно ставится над гласными â, î, û ; буквы с таким знаком (â, î, û) самостоятельными буквами алфавита не считаются. Этот знак служит для обозначения долгот гласных в словах арабского и персидского происхождения, а также зачастую палатализованного («смягчённого») произношения предшествующего такой гласной согласного звука (g, k, l) — подобно тому, как «йотированные» гласные используются в русской кириллице для обозначения «мягкости» предшествующего согласного. Так, слово İsyankâr (бунтарь), в котором присутствует знак â, звучит как «исьянкяр».
- В словацком языке ставится над гласной о (которая при этом выглядит как ô), и читается как «уо». Так, слово stôl (стол) звучит как «стуол».
- В алфавите эсперанто существует 5 согласных букв с циркумфлексом: ĉ, ĝ, ĥ, ĵ, ŝ, которые читаются соответственно [t͡ʃ] , [ʤ], [х], [ʒ] и [ʃ].
- В румынском языке существует 2 гласных буквы с циркумфлексом: â и î, обозначающих звук «ы».
- В валлийском языке используется для обозначения долготы гласных.
- В курдском алфавите есть три буквы с циркумфлексом.
- В инари-саамском и колтта-саамском алфавитах есть буква с циркумфлексом (Ââ).
В математике и физике[править | править код]
- Знак применяется для обозначения математических операторов.
- В физику знак вошёл с развитием квантовой механики, где также используется для обозначения операторов, например, p^{\displaystyle {\hat {p}}} — оператор импульса, H^{\displaystyle {\hat {H}}} — гамильтониан системы. Стоит отметить, что в настоящее время в физических текстах знак оператора нередко опускают, чтобы не загромождать формулу.
В наборе ASCII присутствует другой похожий символ — карет «^» с кодом 5E16. В отличие от циркумфлекса, карет — самостоятельный символ.
Карет используется:
- в языках программирования (например, оператор побитового исключающего ИЛИ в языках с Си-синтаксисом).
- в регулярных выражениях как начало строки или инвертирование группы символов.
- как обозначение нажатия клавиши Ctrl, в том числе для ввода первых 26 символов таблицы ASCII: например, символ с ASCII кодом 0116 (SOH, START OF HEADING) обозначается как Ctrl-A или, что то же самое, ^A.
- в японских смайлах, например ^___^.
- и др.
| |
|---|---|
| Современные латиница, кириллица и некоторые другие системы письма |
|
| Греческое письмо | |
| Старо- и церковнославянская азбука | |
| Арабское письмо | |
| Еврейское письмо | |
| Индийские системы письма |
|
| Кана | |
| Обзорные статьи по системам письма | |
| Примечание: Шаблон содержит специальные символы стандарта Юникод. Если у вас отсутствуют необходимые шрифты, некоторые символы могут отображаться неправильно. | |
| |
|---|---|
| |
Сумма (математика) — Википедия
У этого термина существуют и другие значения, см. сумма.Су́мма (лат. summa — итог, общее количество) в математике — это результат операции сложения числовых величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
- a+b=b+a{\displaystyle a+b=b+a}
- a+(b+c)=(a+b)+c{\displaystyle a+(b+c)=(a+b)+c}
- (a+b)⋅c=a⋅c+b⋅c{\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}
- c⋅(a+b)=c⋅a+c⋅b{\displaystyle c\cdot (a+b)=c\cdot a+c\cdot b}
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы слагаемых множеств, взятые без повторений.
Операция сложение (нахождение суммы) может быть определена для более сложных алгебраических структур. Сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры. В теории категорий определяется понятие суммы объектов.
Пусть в множестве N{\displaystyle \mathbb {N} } находится a{\displaystyle a} элементов, образующих подмножество A{\displaystyle A}, и b{\displaystyle b} элементов, образующих подмножество B{\displaystyle B} (A⊂N,B⊂N{\displaystyle A\subset \mathbb {N} ,B\subset \mathbb {N} }, a и b — натуральные числа). Тогда арифметической суммой a+b{\displaystyle a+b} будет количество элементов c{\displaystyle c}, образующих подмножество C⊂N{\displaystyle C\subset \mathbb {N} }, полученное при дизъюнктном объединении двух исходных подмножеств C=A⊔B;{\displaystyle C=A\sqcup B;}.
Сумму математически обозначают заглавной греческой буквой Σ (сигма).
- ∑i=mnai=am+am+1+am+2+⋯+an−1+an{\displaystyle \sum _{i\mathop {=} m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}}
где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.[1]
В программировании данной процедуре соответствует цикл for.
- Примеры записи
- ∑i=1100i=1+2+3+4+…+99+100{\displaystyle \sum _{i\mathop {=} 1}^{100}i=1+2+3+4+…+99+100}
- ∑i=36i2=32+42+52+62=86{\displaystyle \sum _{i\mathop {=} 3}^{6}i^{2}=3^{2}+4^{2}+5^{2}+6^{2}=86}
Указание границ может опускаться из записи, если они ясны из контекста:
- ∑ai2=∑i=1nai2{\displaystyle \sum a_{i}^{2}=\sum _{i\mathop {=} 1}^{n}a_{i}^{2}}
Итератор может быть выражением, тогда переменная оформляется со скобками как функция «f(){\displaystyle f()}». Например, сумма всех натуральных чисел k{\displaystyle k} в определённом диапазоне:
- ∑0≤k<100f(k){\displaystyle \sum _{0\leq k<100}f(k)}
Сумма f(x){\displaystyle f(x)} элементов x{\displaystyle x} множества S{\displaystyle S}:
- ∑x∈Sf(x){\displaystyle \sum _{x\mathop {\in } S}f(x)}
Сумма μ(d){\displaystyle \mu (d)} всех положительных чисел d{\displaystyle d}, являющихся делителями числа n{\displaystyle n}:
- ∑d|nμ(d){\displaystyle \sum _{d|n}\;\mu (d)}
Несколько символов сигма могут обобщать, например:
- ∑ℓ,ℓ′=∑ℓ∑ℓ′{\displaystyle \sum _{\ell ,\ell ‘}=\sum _{\ell }\sum _{\ell ‘}}
Бесконечная сумма[править | править код]
В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.
Примеры[править | править код]
1. Сумма арифметической прогрессии:
- ∑i=0n(a0+b⋅i)=(n+1)a0+an2{\displaystyle \sum _{i=0}^{n}(a_{0}+b\cdot i)=(n+1){\frac {a_{0}+a_{n}}{2}}}
2. Сумма геометрической прогрессии:
- ∑i=0na0⋅bi=a0⋅1−bn+11−b{\displaystyle \sum _{i=0}^{n}a_{0}\cdot b^{i}=a_{0}\cdot {\frac {1-b^{n+1}}{1-b}}}
3.∑k=1nk3=[n(n+1)2]2=(∑k=1nk)2{\displaystyle \sum \limits _{k=1}^{n}k^{3}=\left[{\frac {n(n+1)}{2}}\right]^{2}=\left(\sum \limits _{k=1}^{n}k\right)^{2}}
4. ∑i=0n(1p)i=pp−1(1−1pn+1),p≠1,n≥0{\displaystyle \sum _{i=0}^{n}{\left({\frac {1}{p}}\right)}^{i}={\frac {p}{p-1}}\left(1-{\frac {1}{p^{n+1}}}\right),\quad p\neq 1,n\geq 0}
Доказательство
- ∑i=0n(1p)i=∑i=0n1⋅1pi=1⋅1−(1p)n+11−1p=pn+1−1pn+1p−1p=pn+1−1pn(p−1)=pp−1(1−1pn+1){\displaystyle \sum _{i=0}^{n}{\left({\frac {1}{p}}\right)}^{i}=\sum _{i=0}^{n}{1\cdot {\frac {1}{p^{i}}}}=1\cdot {\frac {1-{\left({\frac {1}{p}}\right)}^{n+1}}{1-{\frac {1}{p}}}}={\frac {\frac {p^{n+1}-1}{p^{n+1}}}{\frac {p-1}{p}}}={\frac {p^{n+1}-1}{p^{n}(p-1)}}={\frac {p}{p-1}}\left(1-{\frac {1}{p^{n+1}}}\right)}
5. ∑i=0nipi=npn+2−(n+1)pn+1+p(p−1)2,p≠1{\displaystyle \sum _{i=0}^{n}ip^{i}={\frac {np^{n+2}-(n+1)p^{n+1}+p}{(p-1)^{2}}},\quad p\neq 1}
Доказательство
- ∑i=0nipi=∑i=1nipi=p⋅∑i=1nipi−1=p⋅∑i=0n−1(i+1)pi=p⋅(∑i=0n−1ipi+∑i=0n−1pi)=p⋅∑i=0nipi−p⋅npn+p⋅1−pn1−p⇒{\displaystyle \sum _{i=0}^{n}ip^{i}=\sum _{i=1}^{n}ip^{i}=p\cdot \sum _{i=1}^{n}ip^{i-1}=p\cdot \sum _{i=0}^{n-1}(i+1)p^{i}=p\cdot \left(\sum _{i=0}^{n-1}{ip^{i}}+\sum _{i=0}^{n-1}p^{i}\right)=p\cdot \sum _{i=0}^{n}ip^{i}-p\cdot np^{n}+p\cdot {\frac {1-p^{n}}{1-p}}\Rightarrow }
- ⇒(1−p)∑i=0nipi=−npn+1(1−p)+p−pn+11−p⇒∑i=0nipi=npn+2−(n+1)pn+1+p(1−p)2{\displaystyle \Rightarrow (1-p)\sum _{i=0}^{n}ip^{i}={\frac {-np^{n+1}(1-p)+p-p^{n+1}}{1-p}}\Rightarrow \sum _{i=0}^{n}ip^{i}={\frac {np^{n+2}-(n+1)p^{n+1}+p}{(1-p)^{2}}}}
6. ∑i=0npi=(p−1)∑i=0n−1((n−i)pi)+n+1,p≠1{\displaystyle \sum _{i=0}^{n}p^{i}=(p-1)\sum _{i=0}^{n-1}((n-i)p^{i})+n+1,\quad p\neq 1}
Доказательство
- (p−1)∑i=0n−1((n−i)pi)+n+1=(p−1)∑i=0n((n−i)pi)+n+1=(p−1)(n⋅∑i=0npi−∑i=0nipi)+n+1={\displaystyle (p-1)\sum _{i=0}^{n-1}((n-i)p^{i})+n+1=(p-1)\sum _{i=0}^{n}((n-i)p^{i})+n+1=(p-1)\left(n\cdot \sum _{i=0}^{n}p^{i}-\sum _{i=0}^{n}ip^{i}\right)+n+1=}
- =(p−1)(n⋅1−pn+11−p−npn+2−(n+1)pn+1+p(1−p)2)+n+1={\displaystyle =(p-1)\left(n\cdot {\frac {1-p^{n+1}}{1-p}}-{\frac {np^{n+2}-(n+1)p^{n+1}+p}{(1-p)^{2}}}\right)+n+1=}
- =npn+2−np−npn+1+n−npn+2+npn+1+pn+1−p+pn−n+p−1p−1={\displaystyle ={\frac {np^{n+2}-np-np^{n+1}+n-np^{n+2}+np^{n+1}+p^{n+1}-p+pn-n+p-1}{p-1}}=}
- =pn+1−1p−1=∑i=0npi{\displaystyle ={\frac {p^{n+1}-1}{p-1}}=\sum _{i=0}^{n}p^{i}}
- Стоит заметить, что при p=10 {\displaystyle p=10\ } получаем ∑i=0n10i=9⋅∑i=0n−1((n−i)10i)+n+1{\displaystyle \sum _{i=0}^{n}10^{i}=9\cdot \sum _{i=0}^{n-1}((n-i)10^{i})+n+1}, а это последовательность равенств следующего вида:
1=9⋅0+1,11=9⋅1+2,111=9⋅12+3,1111=9⋅123+4,11111=9⋅1234+5{\displaystyle 1=9\cdot 0+1,\quad 11=9\cdot 1+2,\quad 111=9\cdot 12+3,\quad 1111=9\cdot 123+4,\quad 11111=9\cdot 1234+5}
- Стоит заметить, что при p=10 {\displaystyle p=10\ } получаем ∑i=0n10i=9⋅∑i=0n−1((n−i)10i)+n+1{\displaystyle \sum _{i=0}^{n}10^{i}=9\cdot \sum _{i=0}^{n-1}((n-i)10^{i})+n+1}, а это последовательность равенств следующего вида:
Неопределённая сумма[править | править код]
Неопределённой суммой ai{\displaystyle a_{i}} по i{\displaystyle i} называется такая функция f(i){\displaystyle f(i)}, обозначаемая ∑iai{\displaystyle \sum _{i}^{}a_{i}}, что ∀i:f(i+1)−f(i)=ai{\displaystyle \forall i:f(i+1)-f(i)=a_{i}}.
Формула Ньютона — Лейбница[править | править код]
Если найдена неопределённая сумма ∑iai=f(i){\displaystyle \sum _{i}^{}a_{i}=f(i)}, то ∑i=abai=f(b+1)−f(a){\displaystyle \sum _{i=a}^{b}a_{i}=f(b+1)-f(a)}.
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (S) первым ввёл Леонард Эйлер в 1755 году. Как вариант, использовалась греческая буква Сигма Σ. Позднее ввиду связи понятий суммирования и интегрирования, S также использовали для обозначения операции интегрирования.
В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ · ∑).
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
| Символ | Значение |
|---|---|
| α | Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения,поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания |
| β | Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение |
| Γ | Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня |
| γ | Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты |
| Δ | Изменение величины (напр. Δx), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект |
| δ | Небольшое перемещение, дельта-функция Дирака, дельта Кронекера |
| ε | Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия |
| ζ | Дзета-функция Римана |
| η | КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон |
| Θ | Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда |
| θ | Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга |
| κ | Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость |
| Λ | Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон |
| λ | Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана |
| μ | Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон, возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон |
| ν | Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число |
| Ξ | Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон |
| ξ | Длина когерентности, коэффициент Дарси |
| Π | Произведение, коэффициент Пельтье, вектор Пойнтинга |
| π | 3.14159…, пи-связь, пи-плюс мезон, пи-ноль мезон |
| ρ | Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности |
| Σ | Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон |
| σ | Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции,сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина |
| τ | Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули,тангенциальный вектор |
| Υ | Y-бозон |
| Φ | Магнитный поток, поток электрического смещения, работа выхода, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока |
| φ | Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил |
| Χ | X-бозон |
| χ | Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция |
| Ψ | Волновая функция, апертура интерференции |
| ψ | Волновая функция, функция, функция тока |
| Ω | Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция,циклическая частота |
| ω | Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
Символ — Википедия
Материал из Википедии — свободной энциклопедии
Си́мвол (др.-греч. σύμβολον «<условный> знак, сигнал») — знак, изображение какого-нибудь предмета или животного, для обозначения качества объекта[1]; условный знак каких-либо понятий, идей, явлений[2].
Иногда знак и символ различаются, поскольку, в отличие от знака, символу приписывают более глубокое социально-нормативное (духовное) измерение[2].
Понятие символа тесно соприкасается с такими категориями, как художественный образ, аллегория и сравнение. Например, в эпоху поздней античности крест стал символом христианства[3][неавторитетный источник?]. В новейшее время свастика стала символом национал-социализма.
Ф. И. Гиренок обращал внимание, что в современной культуре стёрта разница «между знаком и символом», между тем как спецификой символа является указание на сверхреальное[4].
А. Ф. Лосев определял символ как «субстанциальное тождество идеи и вещи»[5]. Всякий символ заключает в себе образ, но не сводится к нему, поскольку подразумевает присутствие некоего смысла, нераздельно слитого с образом, но ему не тождественного. Образ и смысл образуют два элемента символа, немыслимые друг без друга. Посему символы существуют как символы (а не как вещи) только внутри интерпретаций[6].
В XX веке неокантианец Кассирер обобщил понятие символа и отнес к «символическим формам» широкий класс культурных явлений, таких как язык, миф, религия, искусство и наука, посредством которых человек упорядочивает окружающий его хаос. Ранее ещё Кант доказывал, что искусство, будучи интуитивным способом представления, носит символический характер[7].
- Аверинцев С. С. Заметки к будущей классификации типов символа // Проблемы изучения культурного наследия / Под ред. Г. В. Степанова. — М.: Наука, 1985. — 400 с.
- Аверинцев С. С. Системность символов в поэзии Вячеслава Иванова // Контекст-1989. — М.: Наука, 1989. — 270 с.
- Арутюнова Н. Д. Образ, метафора, символ в контексте жизни и культуры // Res philologica. Филологические исследования. — М.; Л.: Наука, 1990. — 468 с.
- Гордиенко А. Н. Энциклопедия символов. — М.: ЭКСМО, 2007. — 304 с.
- Кассирер Э. Философия символических форм. В 3х томах. — Cassirer Е. Philosophie der symbolischen Formen, L1-3, — Berlin, 1923.
- Кулагина Н. В. Символ как средство мировосприятия и миропонимания: Дис. канд. филос. наук: 09.00.08 / МГУ. — М., 2003.
- Левада Ю. А. Люди и символы: Символические структуры в общественном мнении ([1])
- Лосев А. Ф. Проблема символа и реалистическое искусство. — 2-е изд., испр. — М.: Искусство, 1995. — 320 с.
- Лосев А. Ф. Философско-поэтический символ Софии у Вл. Соловьева // Лосев А. Ф. Страсть к диалектике: Литературные размышления философа. — М.: Советский писатель, 1990. — 320 с.
- Лотман Ю. М. Символ в системе культуры // Лотман Ю. М. Избранные статьи в 3-х т. — Т. 1.: «Статьи по семиотике и типологии культуры». — Таллин: Александра, 1992. — 480 с.
- Лошаков Р. А. Феномен и символ // Вестник Русской Христианской Гуманитаронй Академии. — 2005. — № 6. — С. 73-84.
- Пастуро М. Символическая история европейского Средневековья / Мишель Пастуро; Пер. с франц. Екатерины Решетниковой; Оформление Павла Лосева. — СПб.: Alexandria, 2012. — 448, [16] с. — 3000 экз. — ISBN 978-5-903445-21-9. (в пер.)
- Попов А. В. Символ как фактор текстопорождения: На материале текстов современной русской поэзии Горного Алтая: Дис. канд. филол. наук : 10.02.01. — Барнаул: РГБ, 2006.
- Свасьян К. А. Проблема символа в современной философии: (Критика и анализ). — Ер.: Изд-во АН АрмССР, 1980. — 226 c.
- Солодуб Ю. П. Текстообразующая функция символа в художественном произведении // Филологические науки. — 2002. — № 2. — С. 46—55.
- Сычева С. Г. Проблема символа в философии. — Томск: Изд-во Том. ун-та, 2000. — 197 с.
- Шмеман А. Д. Таинство и символ.
- Энциклопедия символов, знаков, эмблем. — М.: Эксмо; СПб.: Мидгард, 2005. — 608 с., ил. ISBN 5-699-08964-0
- Сикирич Е., Язык символов — язык вечности. — М.: Новый Акрополь, 2011. — 324 с., ил. ISBN 978-5-91896-022-6