Скобка объединения – «Для чего используется фигурная скобка?» – Яндекс.Знатоки — Вебджем.рф

Содержание

Фигурная скобка Википедия

Запрос «:)» и другие, начинающиеся с двоеточия, перенаправляются сюда; об их значении см. Смайлик.

Скобки
()
Изображение

	(: left parenthesis ): right parenthesis
Юни	(: U+0028 ): U+0029
HTML-	(‎: или )‎: или
UTF-16	(‎: 0x28 )‎: 0x29
	(: %28 ): %29

Ско́бки — парные знаки, используемые в различных областях.

Различают:

круглые ( ) скобки;
квадратные [ ] скобки;
фигурные { } скобки;
угловые ⟨ ⟩ скобки (или < > в ASCII-текстах).

Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.).

Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||.

Используются в математике, физике, химии и других науках для установки приоритета выполнения операции в формулах.

Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.

Как репетитор по математике оформляет объединение систем

Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена. Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами

репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?

К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований. Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.

Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:

Когда репетитор по математике вводит квадратную скобку?

К пониманию разницы между скобками лучше всего подводить ученика постепенно, начиная с 8 класса, когда изучается тема «неравенства». В решении самих неравенств восьмиклассники используют понятие «пересечение ответов» . Почему бы репетитору по математике не показать что такое «объединение ответов»? Задачи на объединение присутствуют в учебнике Макарычева, но они ограничиваются операцияями с уже сформированными промежутками. Это не совсем то, что нужно. Вот пример, на котором репетитор по математике мог бы объяснить назначение квадратной скобки: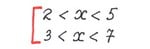

Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).

Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия: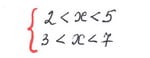

К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения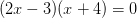

необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.

Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко.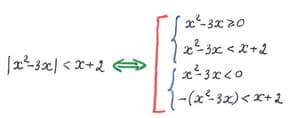

Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.

Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного. Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.

Может ли репетитор по математике обойтись без квадратной скобки

Да, вполне. Для этого применяются стрелочный эквивалент. Например: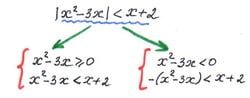

Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение. Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.

Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.

Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.

Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации. При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.

Репетитор по математике, Колпаков А.Н. Москва.

Скобка Википедия

Запрос «:)» и другие, начинающиеся с двоеточия, перенаправляются сюда; об их значении см. Смайлик.

Скобки
()
Изображение

	(: left parenthesis ): right parenthesis
Юни	(: U+0028 ): U+0029
HTML-	(‎: или )‎: или
UTF-16	(‎: 0x28 )‎: 0x29
	(: %28 ): %29

Ско́бки — парные знаки, используемые в различных областях.

Различают:

круглые ( ) скобки;
квадратные [ ] скобки;
фигурные { } скобки;
угловые ⟨ ⟩ скобки (или < > в ASCII-текстах).

Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах), например, 🙂.

Обсуждение:Скобки — Википедия

Материал из Википедии — свободной энциклопедии

Я не въезжаю: с какого бодуна скобками стали слэш, вертикальная линия и двойная вертикальная? И почему тогда забыт бэкслэш? — Тжа0.

Потому что все они (кроме бэкслэша) используются в определённых контекстах в качестве скобок. V1adis1av 12:47, 15 июня 2007 (UTC)

Тогда будьте последовательны: добавьте в шаблон «Скобки ( ( ) ) ( [ ] ) ( { } ) ( < > )» эти знаки. Кстати, ср. текст о косой черте в этой статье и Косая черта. Небо и земля. — Тжа0.

Вот разные скобки:

〈({[⁅<﹝/|…|/﹞>⁆]})〉

Почему скобки ﹝…﹞ и ⁅…⁆ не записаны?—1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 09:17, 18 октября 2015 (UTC)

Видимо, надо написать, что перечисленными примерами (круглые, квадратные, фигурные, угловые) виды скобок не исчерпываются. Кроме того, роль скобок могут играть и комбинации символов, например <tag>…</tag>, это уже зависит от синтаксиса конкретного языка. Vcohen 09:37, 18 октября 2015 (UTC)

Ясно.—1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 10:16, 18 октября 2015 (UTC)

Кстати, есть куча символов для украшения, типа ❨ ❩, ❪ ❫, ❬ ❭, ❮ ❯, ❰ ❱, ❲ ❳ и ❴ ❵, с которых я тоже сделал перенаправления. — 1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 19:27, 4 декабря 2015 (UTC)

И такие: ⦗ ⦘. — 1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 08:48, 24 декабря 2015 (UTC)

Двойные прямые скобки: || или ‖?[править код]

Я тут нашёл значок ‖, и хотел спросить, можно ли поменять || на него. Спасибо за ответ заранее, 1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 10:34, 25 октября 2015 (UTC)

Ещё актуально.—1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 20:11, 31 октября 2015 (UTC)
- Можно предположить, что этот значок для того и введен. Другое дело, что надо попробовать, насколько читабелен он окажется в статье. Vcohen 20:24, 31 октября 2015 (UTC)
  - Спасибо❢ Простите, пожалуйста, а в каком смысле «читабелен»? С уважением, 1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 20:31, 31 октября 2015 (UTC)
    - В смысле насколько он будет разборчив и хорошо виден. Может оказаться, что для наглядности придется оставить как было. Vcohen 20:33, 31 октября 2015 (UTC)
  - Этот значок ‖ (Double Vertical Line, номер в Юникоде: U+2016) не единственный с подобной формой. Можно в качестве двойной прямой скобки использовать ║ (Box Drawings Double Vertical, U+2551) или ∥ (Parallel To, U+2225). Есть ещё буквы разных письменностей, такие как ǁ (Latin Letter Lateral Click, U+01C1), ॥ (Devanagari Double Danda, U+0965) и т.д., но их использовать нежелательно. В LaTeXе двойная вертикальная (в частности, для скобки) обозначается «\|», например <mаth>\| a \| \left\| \frac{b}{c} \right\|</mаth> отображается как ‖a‖‖bc‖{\displaystyle \|a\|\left\|{\frac {b}{c}}\right\|} —V1adis1av 14:45, 1 ноября 2015 (UTC)
    - Спасибо❢—1234qwer1234qwer4^{⇝обс⇜^{⇝вклад⇜}} 20:24, 3 ноября 2015 (UTC)
    - Использовать любые символы не по назначению нежелательно, если это прямо не указанно в стандарте. Например, в стандарте прямо указано, что U+2019 RIGHT SINGLE QUOTATION MARK может использоваться и как кавычка, и как апостроф (что может создавать проблемы, но это другая история). А вот использование символов не по их прямому назначению и конкретнее путаница между U+2016 и U+2551 и U+2225 категорически нежелательны, если не сказать запрещены в нормальных условиях (а они сейчас у всех нормальные, на >95% компьютеров стоят юникодовские шрифты). Не говоря уже про U+01C1 и U+0965.—Любослов Езыкин 10:04, 5 ноября 2015 (UTC)

В статье отсутствуют коды [], {} и др. Надо бы добавить в карточку, там только про круглые скобки. Но не представляю как. Сделал табличку в разделе, наверно туда надо и html коды добавить. —Vladis13 22:18, 11 апреля 2016 (UTC)

Что означают скобки ((( или))) в интернет общении.

смайлик. «))))»улыбочка, «((((«грусть, огорчение, печаль

(((- грусть, )))- радость

)) — улыбка, (( — грусть, недовольство

улыбка грустная ( радостная )

улыбка не довольная, довольная

((( — грусть (((- улыбка

Ско́бки — па́рные знаки, используемые в различных областях. Различают: круглые () скобки; квадратные [ ] скобки; фигурные { } скобки; угловые скобки (или < > в ASCII-текстах) . Обычно первая в паре скобка называется открывающей, а вторая — закрывающей. Почти всегда (за исключением некоторых математических обозначений) открывающая и закрывающая скобки соответствуют друг другу (квадратная — квадратной и т. д.) . Используются также скобки, в которых открывающий и закрывающий знак не различаются, например, косые скобки /…/, прямые скобки |…|, двойные прямые скобки ||…||. В математике, физике, химии и др. используются при написании формул. Различные скобки (как и другие, непарные символы ASCII) применяются в смайликах (эмотиконах) , например, :-). В системе вёрстки TEΧ есть возможность автоматически подстраивать размер скобок под вложенный в него текст: это делается с помощью команд \left и \right. Следует заметить, что во избежание синтаксических ошибок эти две команды всегда должны соответствовать друг другу, однако виды скобок в них — не обязательно. Это делает возможным конструкцию вида «\left\{ a \\ a \right.» для записи систем уравнений.

Это смайлы 🙁 и 🙂 Вот это «)))» — улыбка.

\)(/ , (о/\о) сиськи, (__о__) жопа

Всем насрать на тебя спиногрызина ты лысая

(О^O) — (ОYO)—(0)(0)—(хYx) —( Y ) — сиськи письки короче))

=) Улыбка =(грусть О_о Удивление

)) — веселый двойной подбородок (( — грустный двойной подбородок

) — радость, ( — грусть, ( ͡° ͜ʖ ͡°) — ( ͡° ͜ʖ ͡°).

Тем самым человек после сообщения показывает настроение

) рад, а ( обида

Википедия:Примеры оформления формул — Википедия

Элемент	Синтаксис	Интерпретация в Википедии
Надстрочный индекс	`a^2`	a2{\displaystyle a^{2}}
Подстрочный индекс	`a_2`	a2{\displaystyle a_{2}}
Группировка	`a^{2+2}`	a2+2{\displaystyle a^{2+2}}
Группировка	`a_{i,\;j}`	ai,j{\displaystyle a_{i,\;j}}
Комбинирование верхнего и нижнего индексов	`x_2^3` или `x_{i,\;j}^{x_1,\;x_2}`	x23{\displaystyle x_{2}^{3}} или xi,jx1,x2{\displaystyle x_{i,j}^{x_{1},\;x_{2}}}
Набор индексов	`\sideset{_1^2}{_3^4}\prod_a^b {}_1^2\Omega_3^4`	∏12∏34ab12Ω34{\displaystyle \sideset {_{1}^{2}}{_{3}^{4}}\prod _{a}^{b}\quad {}_{1}^{2}\Omega _{3}^{4}}
Размещение символов друг над другом	`\overset{\alpha}{\omega} \underset{\alpha}{\omega} \overset{\alpha}{\underset{\gamma}{\omega}} \stackrel{\alpha}{\omega}` `\sum_{\begin{smallmatrix}i,\;j=1\\i\neq j\end{smallmatrix}}^\infty a_{ij}`	ωαωαωγαωα∑i,j=1i≠j∞aij{\displaystyle {\overset {\alpha }{\omega }}\quad {\underset {\alpha }{\omega }}\quad {\overset {\alpha }{\underset {\gamma }{\omega }}}\quad {\stackrel {\alpha }{\omega }}\quad \sum _{\begin{smallmatrix}i,\;j=1\\i\neq j\end{smallmatrix}}^{\infty }a_{ij}}
Стрелки с текстом	`A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C`	A←n+μ−1B→Tn±i−1C{\displaystyle A{\xleftarrow {n+\mu -1}}B{\xrightarrow[{T}]{n\pm i-1}}C}
Производная (правильно)	`x'`	x′{\displaystyle x’}
Производная (неправильно в HTML)	`x^\prime`	x′{\displaystyle x^{\prime }}
Производная (неправильно в PNG)	`x\prime`	x′{\displaystyle x\prime }
Сумма	`\sum_{k=1}^N k^2` или `\sum\nolimits_{k=1}^N k^2`	∑k=1Nk2{\displaystyle \sum _{k=1}^{N}k^{2}} или ∑k=1Nk2{\displaystyle \sum \nolimits _{k=1}^{N}k^{2}}
Произведение	`\prod_{i=1}^N x_i`	∏i=1Nxi{\displaystyle \prod _{i=1}^{N}x_{i}}
Предел	`\lim_{n \to \infty}x_n`	limn→∞xn{\displaystyle \lim _{n\to \infty }x_{n}}
Интеграл	`\int\limits_{-N}^{N} e^x\, dx`	∫−NNexdx{\displaystyle \int \limits _{-N}^{N}e^{x}\,dx}
Кратные интегралы	`\iint\limits_{D}^{W} \, dx\,dy`	∬DWdxdy{\displaystyle \iint \limits _{D}^{W}\,dx\,dy}
	`\iiint\limits_{D}^{W} \, dx\,dy\,dz`	∭DWdxdydz{\displaystyle \iiint \limits _{D}^{W}\,dx\,dy\,dz}
	`\iiiint\limits_{D}^{W} \, dx\,dy\,dz\,dw`	⨌DWdxdydzdw{\displaystyle \iiiint \limits _{D}^{W}\,dx\,dy\,dz\,dw}
Интеграл по контуру	`\oint\limits_{C} x^3\, dx + 4y^2\, dy`	∮C⁡x3dx+4y2dy{\displaystyle \oint \limits _{C}x^{3}\,dx+4y^{2}\,dy}
Пересечение	`\bigcap_1^{n} p`	⋂1np{\displaystyle \bigcap _{1}^{n}p}
Объединение	`\bigcup_1^{k} p`	⋃1kp{\displaystyle \bigcup _{1}^{k}p}

«[» и «]» квадратные скобки

Открывающаяся квадратная скобка начинает определение класса символов, закрывающаяся квадратная скобка заканчивает это определение. Сама по себе закрывающаяся квадратная скобка не имеет специального значения. Если закрывающаяся квадратная скобка должна входить в класс символов, то она должна быть первым символом в определении (после начального «^», если нужно), либо должна быть предварена символом обратной косой черты «\».

Класс символов совпадает с единственным символом в исходной строке. Этот символ должен входить в множество, определенное классом, либо, если в начале определения присутствует «^», не входить в это множество. Если требуется включить символ «^» в класс, то он должен быть либо не первым символом в определении, либо перед ним должен быть символ обратной косой черты «\».

К примеру, класс символов [aeiou] совпадет с любой гласной буквой в нижнем регистре, в то время как [^aeiou] совпадет с любым символом, не являющимся гласной в нижнем регистре. Заметьте, что символ «^» это просто удобный способ задания множества символов путем перечисления символов, не входящих в это множество. Класс символов не является утверждением, он потребляет символ из исходной строки и не совпадает, если текущая позиция находится в конце исходной строки.

Когда установлен режим сравнения без учета регистра, символы в определении класса представляют обе версии символа (в верхнем и в нижнем регистре). Так, к примеру, сравнение с классом [aeiou] в режиме без учета регистра будет успешным как для «A» так и для «a», а сравнение с классом [^aeiou] режиме без учета регистра будет неуспешным для «A», в то время как с учетом регистра оно было бы успешным.

Символ перевода строки в классе символов никогда не рассматривается специальным образом, вне зависимости от установки опций PCRE_DOTALL и PCRE_MULTILINE. Так, сравнение [^a] с символом перевода строки всегда будет успешным.

Символ минус «-» может использоваться для указывания диапазонов символов внутри класса. К примеру [d-m] совпадет с любой буквой между «d» и «m» включительно. Если символ минус «-« сам должен присутствовать в классе символов, то перед ним должен стоять символ обратной косой черты «\», либо он должен находится в позиции, когда его нельзя проинтерпретировать как указатель диапазона, то есть в начале или в конце определения класса.

Запрещается указывать символ «]» в качестве конца диапазона символов. То есть шаблон [W-]46] будет проинтерпретирован как класс из двух символов «W» и «-» за которым следует строка «46]» и, таким образом будет совпадение со строками «W46]» или «-46]». Тем не менее, если перед символом «]» стоит символ обратной косой черты «\», то он будет проинтерпретирован как конец диапазона. То есть [W-\]46] будет проинтерпретирован как единственный класс, состоящий из указания диапазона за которым указаны еще два отдельных символа. В качестве конца диапазона может также использоваться восьмеричное или шестнадцатеричное представление символа «]».

Диапазоны указываются для набора символов ASCII. В диапазонах можно использовать числовые коды символов, к примеру: [\000-\037]. Если диапазон включает буквы и установлен режим проверки без учета регистра, то совпадение будет происходить с буквами в любом регистре. К примеру, объявление [W-c] эквивалентно объявлению [][\^`wxyzabc] в режиме без учета регистра.

Типы символов \d, \D, \s, \S, \w и \W также могут использоваться в определениях классов символов, при этом они добавляют в класс символы, которым соответствуют. К примеру, [\dABCDEF] совпадет с любой шестнадцатеричной цифрой. Символ «^» может использоваться совместно с типами символов в верхнем регистре для удобного задания более ограниченных наборов символов, чем те, которые получаются при использовании соответствующего типа символов в нижнем регистре. Так, к примеру [^\W_] совпадет с буквой или цифрой, но не с символом «_».

Хотя любые не алфавитно-цифровые символы, за исключением «\», «-» и «^» (в начале), и завершающего «]» не имеют специального смысла внутри класса символов, ничто не запрещает предварять их символом обратной косой черты «\».

Скобка объединения – «Для чего используется фигурная скобка?» – Яндекс.Знатоки