Скобки символ квадратные: Как поставить квадратные и фигурные скобки в Ворде

Скобки

You can choose among various bracket types to structure a LibreOffice Math formula. Bracket types are displayed in the lower part of the Elements pane. These brackets are also listed in the context menu of the Commands window. All brackets that are not contained in the Elements pane or in the context menu can be typed manually in the Commands window.

Доступ к этой команде

Откройте контекстное меню в окне «Команды», выберите команду Скобки

Выберите Вид — Элементы, затем на панели Элементы выберите Скобки из выпадающего списка.

The following is a complete list of all available bracket types. The icon next to the bracket type indicates that it can be accessed through the Elements pane (menu View — Elements) or through the context menu of the Commands window.

Типы скобок

Круглые скобки

Вставляет заполнитель с нормальными круглыми скобками. Можно также ввести (<?>) в окне Команды.

Квадратные скобки

Вставляет заполнитель в квадратных скобках. Можно также ввести [<?>] в окне Команды.

Двойные квадратные скобки

Вставляет заполнитель с двойными квадратными скобками. Можно также ввести ldbracket <?> rdbracket в окне Команды.

Фигурные скобки

Inserts a placeholder within braces (curly brackets). You can also type lbrace<?>rbrace directly in the Commands window.

Одиночные вертикальные чёрточки

Вставляет заполнитель в вертикальных чёрточках. Можно также ввести lline <?> rline непосредственно в окне Команды.

Двойные вертикальные чёрточки

Вставляет заполнитель в двойных вертикальных чёрточках. Можно также ввести ldline <?> rdline непосредственно в окне Команды.

Угловые скобки

Вставляет заполнитель в угловых скобках. Можно также ввести langle <?> rangle в окне Команды.

Операторные скобки

Вставляет заполнитель в операторных скобках. Можно также ввести langle <?> mline <?> rangle в окне Команды.

Групповые скобки

Вставляет групповые скобки. Можно также ввести {<?>} в окне Команды.

Круглые скобки (масштабируемые)

Вставляет масштабируемые круглые скобки с одним заполнителем. Можно также ввести left(<?> right) в окне Команды.

Квадратные скобки (масштабируемые)

Вставляет масштабируемые квадратные скобки с заполнителями. Можно также ввести left[<?> right] в окне Команды. Размер скобок настраивается автоматически.

Двойные квадратные скобки (масштабируемые)

Вставляет масштабируемые двойные квадратные скобки с заполнителями. Можно также ввести left ldbracket <?> right rdbracket непосредственно в окне Команды. Размер скобок настраивается автоматически.

Фигурные скобки (масштабируемые)

Вставляет масштабируемые фигурные скобки с заполнителем. Можно также ввести left lbrace <?> right rbrace в окне Команды. Размер скобок настраивается автоматически.

Одиночные вертикальные чёрточки (масштабируемые)

Вставляет масштабируемые одиночные вертикальные чёрточки с заполнителем. Можно также ввести left lline <?> right rline в окне Команды. Размер скобок настраивается автоматически.

Двойные вертикальные чёрточки (масштабируемые)

Вставляет масштабируемые двойные вертикальные чёрточки с заполнителем. Можно также ввести left ldline <?> right rdline в окне Команды. Размер скобок настраивается автоматически.

Угловые скобки (масштабируемые)

Вставляет масштабируемые угловые скобки с заполнителем. Можно также ввести left langle <?> right rangle в окне Команды. Размер скобок настраивается автоматически.

Скобки оператора (масштабируемые)

Вставляет масштабируемые скобки оператора с заполнителями. Можно также ввести left langle <?> mline <?> right rangle в окне Команды. Размер скобок настраивается автоматически.

Фигурные скобки сверху (масштабируемые)

Вставляет масштабируемую горизонтальную фигурную скобку сверху с заполнителями. Можно также ввести <?> overbrace <?> непосредственно в окне Команды. Размер скобки настраивается автоматически.

Фигурные скобки снизу (масштабируемые)

Вставляет масштабируемую горизонтальную фигурную скобку снизу с заполнителями. Можно также ввести <?> underbrace <?> непосредственно в окне Команды. Размер скобки настраивается автоматически.

Чтобы вставить нижние скобки, введите lfloor<?>rfloor непосредственно в окне Команды.

Чтобы вставить верхние скобки, введите lceil<?>rceil непосредственно в окне Команды.

Чтобы вставить масштабируемые нижние скобки, введите left lfloor<?>right rfloor непосредственно в окне Команды.

Чтобы вставить масштабируемые верхние скобки, введите left lceil<?>right rceil непосредственно в окне Команды.

Размер скобок настраивается автоматически, если перед командой вставки скобок вводится выражение left и right, например, left(a over b right). Можно также установить размер и интервал для скобок путём последовательного выбора команд Формат — Интервал — Категория — Скобки и установки необходимых процентных отношений. Установите флажок Масштабировать все скобки, чтобы применить эти изменения ко всем скобкам в формуле.

Также можно использовать одиночную скобку. Для этого введите обратную косую черту \ перед командой. Например, при вводе \[ левая квадратная скобка отображается без закрывающей скобки. Это удобно при создании непарных скобок или при создании интервала. Заметьте, что по отдельности могут быть использованы только немасштабирующиеся скобки. Для изменения размера используйте команду size.

Примеры одиночных скобок

Для немасштабируемых скобок:

a = \{ \( \[ b newline

{} + c \] \) \ }

Для масштабируемых скобок используйте none в качестве имени скобки

a = left ( a over b right none newline

left none phantom {a over b} + c right )

Инструкция phantom гарантирует установку правильного размера для последней скобки.

Не забудьте ввести пробелы между элементами при их вводе непосредственно в окне «Команды». Это обеспечит правильную структуру формулы.

Полезные сведения об индексах и показателях степени, а также о масштабировании помогут правильно структурировать формулы. Дополнительные сведения о скобках см. в разделе Скобки и группы.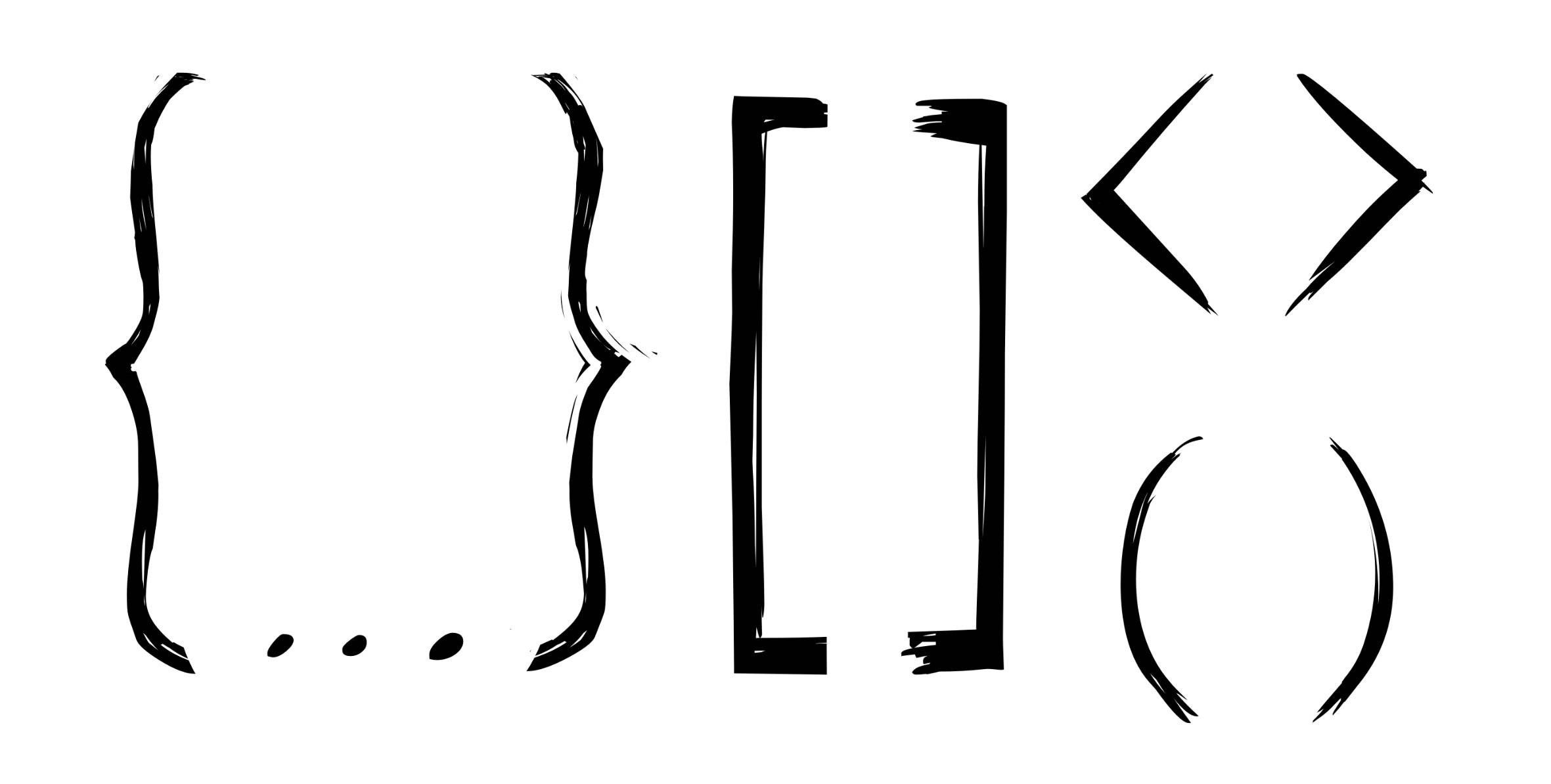

Как правильно использовать скобки в математике

Открывая математические правила и законы, ученые одновременно с этим разрабатывают знаки, обозначения и символику. Знаки и символы в математике, в том числе, действия в скобках, — условные обозначения, которые применяют при записи специальных понятий, терминов и выражений. Это своеобразный язык, позволяющий максимально упростить и сократить подачу информации, выразить мысль предельно точно, избежать ошибок, двусмысленных трактовок. Скобки — одни из символов, применяемых особенно часто.

Данная статья посвящена применению скобок при решении задач в математике, действия с ними, область их использования, основные разновидности. Приведены основные термины и методы их применения для различных задач. Имеются примеры с разъяснениями.

Математика: действия со скобками различных видов

Скобки — парные (за небольшим исключением) знаки. Первая называется открывающей, вторая — закрывающей. Они отграничивают определенную часть математического выражения, помогая определиться с порядком выполнения действий. {3}\] и т. д.;

указание координат точек в одно- и многомерных системах;

компактная запись периодических десятичных дробей;

запись отрицательного числа в математическом выражении с целью разделения знаков математического действия и самого числа.

Круглые скобки помогают определиться с последовательностью и приоритетом логических операций и математических действий (как вариант, для изменения существующего алгоритма).

Квадратные знаки применяют для:

• указания целой части числа;
• взятия модуля числа;
• определения порядка действий, аналогично круглым;
• операций с векторами;
• указания скобок второго уровня;
• записи координат, массивов чисел.

Помимо математики, квадратные скобки применяют при записи физических, химических формул, в программировании.

Фигурные скобки ({) используют при обозначении множеств, для объединения уравнений или неравенств в систему, как скобки третьего уровня. Их также применяют при решении систем уравнений (пересечение множеств), а квадратные — [используют для записи их объединения (так называемые совокупности). Рассмотрим примеры с этими символами более подробно.

Принципы раскрытия, примеры по математике со скобками

Рассмотрим порядок выполнения действий с примерами со скобками в математике, правила их использования.

Правила

Правило 1. Если перед скобками поставлен плюс, — знаки чисел, заключенных внутри, остаются
неизменными. Пример: \[4+(5-1-2+3)=4+5-1-2+3\]

Правило 2. Если перед скобками поставлен минус, то знаки чисел, находящихся внутри, при
раскрытии меняются на противоположные.
Пример: \[a-(b+c-k)=a-b-c+k\]

Правило 3. Если перед скобками или после них находится знак «умножение», — получаемый
результат зависит от выполняемых действий.
Примеры:

Примеры с умножением: \[3 \cdot(2 \cdot 4 \cdot 6 \cdot 9)=3 \cdot 2 \cdot 4 \cdot 6 \cdot 9 ;(3 \cdot 2
\cdot 9) \cdot 4=3 \cdot 2 \cdot 9 \cdot 4\]

Примеры с делением: \[3 \cdot(15: 5)=(3-15): 5=(3: 5) \cdot 15 ;(10: 2) \cdot 3=(3 \cdot 10): 2=(3: 2) \cdot
10\]

Правило 4. если перед скобками либо после них поставлен знак «деление», то результат зависит
от того, какие действия выполняют внутри них.

Порядок выполнения действий со скобками в математике

Самое частое использование скобок — указание алгоритма выполнения действий. С этой целью используют круглые символы, одну или несколько пар. Порядок решения — следующий:

• действие в скобках;
• умножение, деление;
• сложение, вычитание.

---

Пример №1. Если задано выражение 7 + 3 — 1, то действия выполняют последовательно. Порядок действий меняется, если задействовать скобки. Например, в выражении (7 + 3) — 1 вначале выполняют сложение, заключенное в скобки. Результат останется тем же: 9. Если записать выражение, обособив при этом вычитание 7 + (3 — 1), вначале выполняют вычитание в скобках, а затем сложение с числом 7. В данном примере окончательный результат остается тем же.

---

Пример №2. Рассмотрим, когда от расположения скобок в математическом выражении зависит результат. В выражении \[7+3 \cdot 4\] очевидно, что вначале следует выполнить умножение. Получаем результат 19. Если выражение будет выглядеть как \[(7+3) \cdot 4\], то сначала выполняют сложение в скобках. Конечный результат — 40.

---

Пример №3. В выражении \[(5 \cdot(8-4)+6): 2\] вначале отнимают 4 от 8. Полученный результат умножают на 5. К произведению прибавляем 6. Последним действием будет деление на 2.

Нередко можно встретить символы различного размера. Делают это из соображений удобства, чтобы упростить порядок действий и переход от одного вычисления к другому. Внутренние скобки всегда меньше внешних. Например, \[\left(\left((7-2): 2+\frac{1}{2}\right)+4-\frac{1}{4} \cdot 5\right) \cdot 3-5\]. Можно также воспользоваться квадратными знаками: \[[4+7 \cdot(4-3)] \cdot 5\]. Или оформить пример символами фигурными: \[{6+[6-12(7-4): 3]+8-4}:[4+7+5:(6-4-1)]\]. Чтобы получить правильный результат, нужно вначале определиться с порядком действий и парами скобок. Чтобы упростить задачу, можно воспользоваться различными их типами или выделять каждую пару «своим» цветом. Последний вариант используется нечасто, так как занимает много времени и попросту неудобен. Использование сочетаний круглых, фигурных и квадратных знаков удобнее.

Скобки в математике и отрицательные числа

Для отображения отрицательных чисел пользуются круглыми символами. Примеры:

\[7+(-3)+(-4) \cdot(-6), 9+\left(-\frac{3}{4}\right), 4 \frac{6}{7}+\left(-3 \frac{4}{7}\right), 3 \frac{6}{8}-\frac{4+\left(-\frac{1}{8}\right)}{5 \cdot(-2) \cdot(-2,5)}\]

Если отрицательное число находится в начале выражения, его не заключают в скобки. Пример: \[-3 \cdot 4+(-8): 2\]. Отрицательное число -3 в начале выражения можно записывать без скобок. Еще один пример: \[\frac{2-1,5}{-2,3 \cdot(4+6)+(5-3): 2}\]. Число -2,3 в знаменателе находится в самом начале, поэтому подобное обособление не является обязательным. Впрочем, можно записать эти же выражения и со скобками. Примеры: \[(-3) \cdot 4+(-8): 2\] или \[\frac{2-1,5}{(-2,3) \cdot(4+6)+(5-3): 2}\]. {1}(\cos 3 x-\sqrt{2}) \mathrm{d} x, \iiint(5 x y+2 z) \mathrm{d} x \mathrm{~d} y \mathrm{~d} z\].

Отделение аргумента функции скобками

Записывая функцию, как правило, пользуются круглыми скобками. Если функция обозначена литерой f, а аргумент — x, то общий вид функции — \[f(x)\]. При наличии нескольких аргументов функция имеет вид \[F(x, t, z)\].

Особенности написания периодических дробей

Скобки применяют при записи периодических дробей — в них заключают период. Например, если дробь имеет вид 0,54545454…, то ее можно записать в более компактном виде, характерном для периодических дробей: 0,(54). Еще один пример рациональной записи периодической дроби: 0,46(27). В обычном виде она выглядит следующим образом: 0,4627272727….

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Числовые промежутки

Существует несколько вариантов записи числовых промежутков при помощи различных сочетаний круглых и квадратных скобок: (), (], [), []. Внутри границ указывают промежутки, в которых функция имеет смысл. Круглый символ означает, что число не принадлежит области определения, квадратный — принадлежит. Если при записи числового промежутка фигурирует знак бесконечности, то пользуются круглыми скобками.

Примеры: \[(0,3),\left[\frac{1}{2}, 15\right),\left(-5 \frac{1}{3},-1 \frac{3}{4}\right),[4,800],(-\infty,-8],(-5,+\infty), (-\infty,+\infty)\].

Иногда вместо круглых ограничений можно встретить обратные квадратные. Например, выражения  \[(0,3) \text { и }] 0,3[\] — идентичны. Смысл выражения остается прежним.

Запись числовых промежутков с помощью знаков различных видов сведена в таблицу.

Наименование промежутка	Обозначение	Запись при помощи неравенства
Открытый интервал	\[(a ; b)\]	\[a<x<b\]
Отрезок (сегмент)	\[[a ; b]\]	\[a \leq x \leq b\]
Полусегмент	\[[a ; b)\]	\[a \leq x<b\]
Полусегмент	\[(a ; b]\]	\[a<x \leq b\]
Луч	\[(-\infty ; c]\]	\[x \leq c\]
Все числа координатной прямой	\[(-\infty ;+\infty)\]	\[x \in R\]
Пустое множество	\[\varnothing\]	\[x \in \emptyset, x \in \] {}

Отображение систем и совокупностей уравнений

Системы уравнений, неравенств, а также системы, содержащие как уравнения, так и неравенства, используют с фигурной скобкой {, размещенной слева. {2}-1} \end{array}\right.\]

Пример 2:

\[\begin{gathered} {\left[\begin{array}{c} x>3 \\ 2 x-3 y=8 \\ 2 x+5 y \geq 1 \end{array}\right.} \end{gathered}\]

Можно также встретить сочетание системы с совокупностью.

Применение фигурных скобок для отображения кусочных функций

При записи кусочных функций применяют фигурные скобки, которые определяют функцию формулы с указанием числовых промежутков.

Пример

Функция модуля: \[|z|=\left\{\begin{array}{l}
z, \text { при } \geq 0 \\
-z, \text { при } z<0
\end{array}\right.\]

Обозначение координат точки

С этой целью применяют круглые скобки, в которых записывают координаты точки на прямой, в двух- или трехмерной координатной система. Возможна также запись координат точки, расположенной в n-мерном пространстве.

Пример 1: \[B(4)\]. Это означает, что точка B имеет на прямой координату 4.

Пример 2: \[k(1,3,5)\]. Точка k имеет координаты 1, 3 и 5 соответственно по осям абсцисс, ординат и аппликат.

Пересечение элементов множества

Пересечение элементов множества — один из вариантов их описания. Элементы множества записывают через запятую, заключив внутрь фигурных скобок. Пример такой записи: C= {1, 5, 8}. Множество содержит 3 элемента: числа 1, 5 и 8.

Координаты вектора

Это понятие используют при рассмотрении векторов в некоторой координатной системе. Координаты вектора записывают в фигурных или круглых скобках поочередно. Примеры записи координат векторов в двухмерной системе: \[\vec{b}_{\{0,-4\}} \text { или } \vec{b}(0,-4)\]. Такая запись означает, что вектор имеет координаты по осям абсцисс и ординат 0 и -4 соответственно. Если вектор рассматривается в пространственной координатной системе, внутри скобок указывают три координаты.

Пример 1: \[\overrightarrow{B C}\left(0,-4, \frac{3}{5}\right)\].

В вузах принята иная запись векторов в системе координат: над буквенным обозначением вектора, как правило, не ставят черточку или стрелку. Координаты записывают внутри скобок по очереди, разделяя их запятыми.

Пример 2: \[a=\left(3,5,7, \frac{1}{2}, 9\right)\]. Так записывают вектор в пятимерной системе.

Есть и иная форма записи: в круглых скобках столбиком.

Запись матричных элементов

Скобки используют при написании матриц. Элементы последних заключают в парные круглые скобки. Иногда вместо круглых знаков пользуются квадратными. При этом матрицы имеют одинаковый смысл, получаются равнозначными.

Надеемся, что приведенный материал окажется полезным при подготовке уроков математики.

Что такое квадратная скобка ( ] ) и как ее использовать?

Из различных типов скобок большинство людей, вероятно, скажут, что скобки — это те, которые они знают лучше всего. Идя дальше, некоторые люди могут даже не знать, что существуют другие типы брекетов. Хотя квадратные скобки могут использоваться не очень часто, они часто имеют решающее значение для авторов, которые обсуждают особенно сложную цитату.

Вы никогда не знаете, когда этим бедным писателем окажетесь вы, поэтому неплохо подготовиться и узнать, как лучше всего использовать квадратные скобки в своем письме.

Что такое квадратных скобок ?

Квадратные скобки , часто называемые просто скобками в американском английском, представляют собой набор знаков препинания, которые чаще всего используются для изменения или добавления информации к цитируемому материалу. Квадратные скобки идут парами как [ и ] . Квадратные скобки напоминают круглые скобки и используются так же, но эти два знака препинания НЕ взаимозаменяемы.

✏️

Примеры

В следующих предложениях показано, как мы используем квадратные скобки. Вы заметите, что почти все примеры содержат цитаты.

• По данным полиции, подозреваемый «прятал [на дереве] в течение двух дней, прежде чем его поймали».
• Сенатор сказал: «Мы должны были из [sic] с самого начала вкладывать больше денег в образование».
• Решение судьи заключалось в том, что «две команды [Львы и Тигры] обе нарушили правила».
• Если вам нужна помощь, позвоните по моему номеру телефона. (Это [555] 123-4567.)

Когда вы используете квадратные скобки?

В целом квадратные скобки используются гораздо реже, чем круглые в письменной форме. В большинстве случаев они используются для изменения или предоставления дополнительного контекста цитатам. Часто писатели корректируют свою работу или перефразируют текст вокруг цитаты, чтобы вообще не использовать квадратные скобки. Однако иногда использование квадратных скобок может быть неизбежным, поэтому полезно знать, когда вам может понадобиться их использовать.

Цитаты

Как правило, наиболее распространенная причина, по которой вам нужно использовать квадратные скобки, связана с цитатами.

Во всех руководствах по стилю, грамматических ресурсах и этических рекомендациях будет сказано, что недопустимо изменять формулировку цитаты, чтобы изменить ее значение или приписать слова человеку, которого они никогда не говорили.

Однако иногда необходимо изменить цитату или добавить к ней дополнительный контекст, чтобы помочь читателю понять, о чем идет речь. Квадратные скобки позволяют сделать это, давая понять, что все, что заключено в квадратные скобки, не является частью исходного текста или заявления.

Когда дело доходит до кавычек, есть несколько причин использовать квадратные скобки.

Пояснение

Иногда цитата не имеет смысла вне контекста, в котором она была первоначально использована, или она ссылается на что-то другое, сказанное ранее. В этом случае автор может использовать квадратные скобки, чтобы добавить поясняющую информацию для читателя. Например,

• Исходное утверждение: «Я люблю свою кошку. Ее зовут Нина, и она великая охотница. Нина любит есть мышей и убивать птиц».
• Цитата в квадратных скобках: Он сказал: «Нина [его кошка] любит есть мышей и убивать птиц».

Добавление дополнительной информации

Иногда цитата нуждается в дополнительной информации, которая изначально не упоминалась, чтобы она была понятна читателю. Опять же, мы можем использовать квадратные скобки, чтобы добавить эту информацию:

• Исходное утверждение: «Это знаменательный день. Эти две нации объединились в дружбе, и для меня большая честь быть частью этого».
• Цитата в квадратных скобках: Посол сказал, что это «знаменательный день». Идя дальше, она сказала: «Эти две нации [Рохан и Гондор] объединились в дружбе».

Коррекция цитаты по грамматическим причинам

Иногда цитата грамматически не соответствует авторскому тексту. Например, первоначальный оратор мог говорить от первого лица, а автор цитирует его от третьего лица. Квадратные скобки могут использоваться для обозначения того, что автор корректирует цитату по грамматическим причинам.

• Исходное заявление: «Я люблю майонез. Я даже добавляю его в хот-доги».
• Цитата в квадратных скобках: Она сказала, что « [она] любит майонез » и что « [она] даже кладет [ей] его на хот-доги».

Обнаружение грамматической ошибки в исходной цитате

Поскольку большинство авторов вообще не меняют цитаты, некоторые цитаты могут содержать грамматические ошибки, опечатки или другие ошибки. Квадратные скобки можно использовать, чтобы указать читателю, что ошибка присутствовала в исходном источнике. В этом случае термин sic часто используется в квадратных скобках, чтобы указать, что ошибка присутствовала в исходном источнике.

• Исходное утверждение: «Самый большой десерт на Земле на самом деле находится в Антарктиде».
• Цитата в квадратных скобках: Я был удивлен, узнав, что самая большая пустыня на самом деле находится в холодном месте. В моем учебнике по географии написано: «Самый большой десерт [так в оригинале]
  на Земле на самом деле находится в Антарктиде».

Скобки внутри скобок

Некоторые руководства по стилю или ресурсы по грамматике могут разрешать использование квадратных скобок, чтобы избежать использования набора скобок внутри другого набора скобок. Например,

• Джо все сделал сам. (Он никогда не просит помощи у меня [или кого-либо еще] .)

Однако правила, касающиеся этого конкретного случая, не являются универсальными. Лучше всего обратиться к руководству по стилю или ресурсу по грамматике, который вы используете, если вы когда-нибудь столкнетесь с такой ситуацией.

Сделайте свое письмо блестящим!

Получайте советы по грамматике, советы по письму и многое другое на Thesaurus. com… прямо в свой почтовый ящик!

Как использовать квадратные скобки

В большинстве случаев квадратные скобки подчиняются всем тем же правилам оформления скобок. Однако квадратные скобки, как правило, проще использовать, поскольку они обычно не содержат полных предложений.

Квадратные скобки всегда идут парами

Как и скобки, использование только одной квадратной скобки считается грамматической ошибкой. Дополнительная информация должна быть полностью заключена в две квадратные скобки:

❌ Неверно: Лесли Митчеллс из Канады] выиграла золотую медаль.
✅ Правильно: Лесли Митчеллс [из Канады] выиграла золотую медаль.

Капитализация

Первая буква в квадратных скобках обычно не пишется заглавной, поскольку квадратные скобки обычно содержат фрагменты предложений, отдельные слова или отдельные буквы/символы. Однако имена собственные обычно пишутся с заглавной буквы, даже если они используются отдельно в квадратных скобках.

✅ Правильно: Зак сказал: «Я могу научить [йоге] любого, кто хочет учиться».
✅ Также верно: Власти Whoville ищут «ворчливого зеленого монстра, который ненавидит [Рождество] ».

Идеальная пунктуация с Grammar Coach™

Запутались в пунктуации и ее правильном использовании? Платформа Thesaurus.com Grammar Coach™ значительно упрощает написание статей, эссе, электронных писем и многое другое. Этот инструмент для письма использует технологию машинного обучения, специально разработанную для выявления грамматических и орфографических ошибок. Его Synonym Swap найдет лучшие существительные, прилагательные и многое другое, чтобы помочь вам выразить то, что вы на самом деле имеете в виду, и поможет вам писать четче и сильнее.

Когда использовать квадратные скобки […]

Из четырех типов скобок, встречающихся в английских знаках препинания, квадратная скобка является одной из самых популярных. Наряду со скобками квадратная скобка используется для разделения слов в тексте для добавления деталей и информации.

Разница между скобками и квадратными скобками важна, так как каждая из них разделяет разные типы информации. Прочтите множество примеров, чтобы узнать, как правильно использовать квадратную скобку.

Для чего используются квадратные скобки?

Квадратные скобки […], также называемые скобками, представляют собой знаки препинания, используемые для изменения или добавления информации к цитируемому материалу. Они всегда используются парами и помогают отделить информацию от остальной части предложения, чтобы добавить информацию или детали. Это похоже на то, как вы используете круглые скобки (также называемые круглыми скобками). Тем не менее, квадратные и круглые скобки не могут использоваться взаимозаменяемо.

В чем разница между квадратными скобками и круглыми скобками?

Квадратные скобки почти всегда используются в кавычках, чтобы сделать цитату более ясной и понятной. Они компенсируют слова, которые помогают уточнить, подчеркнуть или исправить прямую цитату.

Скобка — это тип скобки, также известный как круглая скобка. Они используются для смещения слов в текстах, чтобы добавить дополнительную информацию и детали. Слова, находящиеся в скобках, не нужны для понимания отрывка, тогда как скобки часто нужны, чтобы читатель понял цитату.

Двумя другими типами скобок являются угловые скобки (также известные как шевроны) и фигурные скобки (также известные как скобки или фигурные скобки).

Правила использования квадратных скобок 

Существуют определенные правила использования квадратных скобок. Эти правила и примеры предоставляют информацию, необходимую для правильного использования в письме, и помогают сделать цитируемый материал понятным и уместным.

Правило №1

Используйте скобки для уточнения неясных существительных и местоимений в цитате.

Например,

• Он четко заявил, что «не будет слияния с компанией [солнечной фермы] из-за их неэффективной практики борьбы с сорняками, в которой использовались высокотоксичные средства борьбы с сорняками, которые разрушали почву».

Правило №2

Используйте скобки для перевода иностранного слова или фразы в цитате.

Например

• Несмотря на то, что она четыре года изучала немецкий язык в старшей школе, она «боролась с элементарными приветствиями, находясь в деревне, часто отвечая ich weiss nicht [я не знаю], когда говорят на местном диалекте».

Правило №3

Используйте скобки, чтобы указать изменение первой буквы цитируемого материала с прописной на строчную или наоборот.

Например,

• В 1913 году ее дедушка «в возрасте 12 лет один приехал на остров Эллис, чтобы воссоединиться со своей семьей, которая путешествовала по угольным шахтам Нью-Мексико».

Правило № 4

Используйте скобки вокруг латинского термина sic, означающего «таким образом» или «так», чтобы указать на ошибку или необычное употребление слова в цитате. Это указывает на то, что исходный писатель включил ошибку.

Например,

• На нашем местном ипподроме проводились «любительские джекпоты каждый четверг, пятницу и каждую [sic] другую субботу утром».

Вы также можете использовать исправление исходного материала со знаком вопроса, если вы угадываете исправление.

Например,

• «Профессор истории путешествовал по миру, включая такие отдаленные места, как острова Керглен [острова Кергелен?].

Правило №5

Используйте скобки, чтобы указать, когда вы меняете цитату, чтобы подчеркнуть определенную часть отрывка.

Например,

• Профессор поделился своими опасениями по поводу того, сколько студентов «отнеслись к процессу обучения безразлично и были готовы выбросить деньги за обучение, если они пропустили урок [выделено автором]».

Правило № 6

Используйте квадратные скобки для цензуры любых неприемлемых материалов, обнаруженных в исходном тексте.

Например

• Она потеряла хладнокровие с группой, сказав им «сесть [ругательство] вниз».

Правило №7

Используйте квадратные скобки внутри скобок для замены скобок внутри скобок.

Например,

• Мы путешествовали исключительно на машине, когда дети были маленькими (чтобы мы могли перестать [знакомить их с историей] всякий раз, когда захотим).

Когда использовать скобки для ссылок:

Скобки иногда используются для обозначения ссылок и сносок. Всегда обязательно сверяйтесь с руководством по стилю, которое вы используете, для правильного использования и любых применимых обновлений при использовании скобок таким образом.

Например, в руководствах по стилю APA вы можете увидеть скобки, используемые для обозначения следующего: 

• Определение контекста публикации (например, диссертации)
• Определение источника (например, произведения искусства, социальные сети или брошюры)
• Указание, когда источник не имеет номера страницы (например, видео, мобильное приложение или ветка чата)
• Предоставление переводов названий с другого языка

Использование квадратных скобок в этих сценариях позволяет читателю узнать, что предоставленная информация не появляется в реальной работе, но, тем не менее, является точной.

Сноски также появляются после информации как [1], [2] и [3], где это уместно, чтобы предоставить читателю ссылку, где он может найти фактическую цитату используемого материала. Всегда разделяйте числа скобками, а не включайте их в один длинный список, когда требуется более одного.

Квадратные скобки Примеры написания

Скобки являются приемлемым знаком препинания, который можно использовать как в формальном, так и в неформальном употреблении при цитировании материалов.

И еще: «Возможно, кто-нибудь поймет намек и объяснит [назначение квадратных скобок]». (Хранитель)

Говоря о сомнениях, почему, ну почему кто-то сомневался в оценке MWD о том, что [Скучная] субботняя газета Морри Шварца скучна? (Австралийский)

Давайте рассмотрим

Квадратные скобки, также называемые скобками, — это один из четырех различных типов скобок, используемых для смещения слов в различных текстах. Квадратные скобки обычно используются для цитируемого материала, чтобы помочь определить и разъяснить читателям прямые цитаты.