SVG — матричные преобразования — Все о web разработке на xdan.ru
Когда вы рисуете в SVG, матричная математика используется для того, чтобы понять как сейчас выглядит исходный объект и где на экране он находится. К примеру есть некий элемент 200*200 пиксел, но отобразить его надо на холсте размером 100 на 100. Точка (20,20) должна будет нарисована в (10,10) на холсте. Такую трансформацию нужно сделать для каждой точки элемента. При работе с SVG браузер делает это за вас, используя матричную математику.
Матричная математика делает множество различных типов трансформаций очень простыми. Тем не менее, матричная математика не позволяет сделать с объектом такие операции, как перекос, скрутка или изгиб. SVG позволяет добавить трансформацию к объекту при помощи матриц, до того, как объект будет отображен на экране. Следующее демо позволяет играть параметрами трансформации и увидеть результат визуально.
<g transform="scale(5) translate(15, 15) rotate(20) skewX(20) skewY(5)"> <rect x="10" y="10" fill="firebrick" /> <circle r="10" fill="seagreen" stroke="blue"/> <rect x="5" y="5" fill="gray" stroke="silver"/> </g> |
svg» type=»image/svg+xml»/> (Загрузить) |
Псевдо функции разделенные пробелами в примере, применяются в порядке написания. Функции накладывают атрибут transform для всех вложенных элементов ‘g’,’svg’,’image’ или любой другой элемент. Шаблоны и градиенты имеют атрибуты, к которым также применяется трансформация.
- translate(x, y)
- scale(sx, sy)
- rotate(angle, cx, cy)
- skewX(angle)
- skewY(angle)
- matrix(a, b, c, d, e, f)
Смещение
translate(x, y)
Перемещает точки объекта на x и y координат. Если ‘y’ не задано, тогда считается что она равна 0. Трансформация сдвига это фундаментальная операция, и накладывается она на все последующие трансформации.
Сжатие
scale(sx, sy)
Трансформация сжатия, вдоль осей x и y.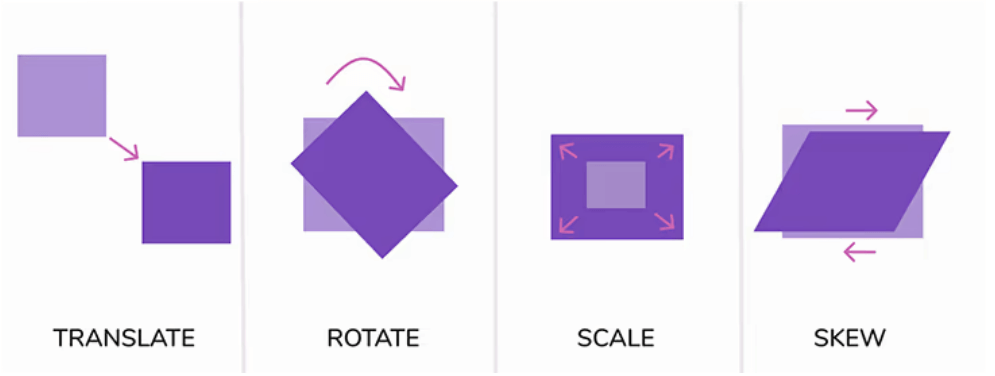 Если sy не задано, то трансформация идет пропорционально и обе оси трансформируются по заданному sx
Если sy не задано, то трансформация идет пропорционально и обе оси трансформируются по заданному sx
Вращение
rotate(angle, cx, cy)
Вращение точек вокруг координаты (cx, cy) на угол angle. Точка (cx, cy) это смещение от текущего местоположения. Если cx и cy не заданы, то вращение будет происходит вокруг текущей позиции
Скос
skewX(angle)
skewY(angle)
Скос вдоль оси определяется используемой функцией. Расстояние на которое происходит скос это тангенс угла angle
Matrix
matrix(a, b, c, d, e, f)
Это преобразование напрямую умножает текущую матрицу преобразования на ту, которая подается в эту функцию. Функции до этого позволяют все то же самое, но делают это более понятно
Порядок операций
При матричных преобразованиях, очень важен порядок преобразований. Смещение, а затем вращение дает иной результат, чем сперва вращение а потом смещение. Преобразования могут быть вложенными.Это показано ниже. окончательный результат в зеленом, не в той же самой позиции, хотя к нему были применены те же самые преобразования.
Смещение, а затем вращение дает иной результат, чем сперва вращение а потом смещение. Преобразования могут быть вложенными.Это показано ниже. окончательный результат в зеленом, не в той же самой позиции, хотя к нему были применены те же самые преобразования.
При матричных преобразованиях нужно несколько раз подумать прежде чем выстроить порядок трансформаций. Только проверив все саим, вы найдете верное решение
<!-- Смещение и вращение-->
<use xlink:href="#example" fill="red" />
<g transform="translate(15, 15)" fill="yellow">
<use xlink:href="#example" />
<g transform="rotate(30)" fill="green">
<use xlink:href="#example" />
</g>
</g>
<!-- Вращение и смещение -->
<g transform="translate(65)">
<use xlink:href="#example" fill="red" />
<g transform="rotate(30)" fill="yellow">
<use xlink:href="#example" />
<g transform="translate(15, 15)" fill="green">
<use xlink:href="#example" />
</g>
</g>
</g>Преобразование
— SVG: Масштабируемая векторная графика
Атрибут преобразования определяет список определений преобразования, которые применяются к элементу и его дочерним элементам.
Примечание: Начиная с SVG2, transform является атрибутом представления, что означает, что его можно использовать как свойство CSS. Однако имейте в виду, что существуют некоторые различия в синтаксисе между свойством CSS и атрибутом. См. документацию по свойству CSS 9.0004 преобразуйте для конкретного синтаксиса, который будет использоваться в этом случае.
Этот атрибут можно использовать с любым элементом SVG.
html,
тело,
свг {
высота: 100%;
}
В SVG 1. 1 разрешалось использовать только эти 16 элементов:
1 разрешалось использовать только эти 16 элементов: , , , , , 4 , Object
, <изображение> , <строка> , <путь> , <полигон> ,
, , и ). Кроме того, унаследованные от SVG 1.1, и поддерживают атрибут gradientTransform , а поддерживает атрибут patternTransform , оба из которых действуют точно так же, как 9004 преобразовать атрибут .
| Значение | <список-преобразования> |
|---|---|
| Значение по умолчанию | нет |
| Анимируемый | Да |
Следующие функции преобразования могут использоваться атрибутом transform
Предупреждение: В соответствии со спецификацией вы также должны иметь возможность использовать функции преобразования CSS.
Matrix
Функция преобразования matrix( задает преобразование в форме матрицы преобразования из шести значений. matrix(a,b,c,d,e,f) эквивалентно применению матрицы преобразования:
(acebdf001)\begin{pmatrix} a & c & e \ b & d & f \ 0 & 0 & 1 \end{pmatrix}, который отображает координаты из предыдущей системы координат в новую систему координат с помощью следующих матричных равенств:
(xnewCoordSysynewCoordSys1)=(acebdf001)(xprevCoordSysyprevCoordSys1)=(axprevCoordSys+cyprevCoordSys+ebxprevCoordSys+dyprevCoordSys+f1) \begin{pmatrix} x_{\mathrm{newCoordSys}} \ y_{\mathrm{newCoordSys}} \ y_{\mathrm{newCoordSys}}ma } = \begin{pmatrix} a & c & e \ b & d & f \ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_{\mathrm{prevCoordSys}} \ y_{\mathrm{prevCoordSys} } \ 1 \ end {pmatrix} = \ begin {pmatrix} a x _ {\ mathrm {prevCoordSys}} + c y _ {\ mathrm {prevCoordSys}} + e \ b x _ {\ mathrm {prevCoordSys}} + d y _ {\ mathrm{prevCoordSys}} + f \ 1 \end{pmatrix}
Пример
HTML,
тело,
свг {
высота: 100%;
}
w3.org/2000/svg"><прямоугольник х = "10" у = "10" заполнить = "красный" трансформировать="матрица(3 1 -1 3 30 40)" />
Translate
Функция преобразования translate( перемещает объект на x и y .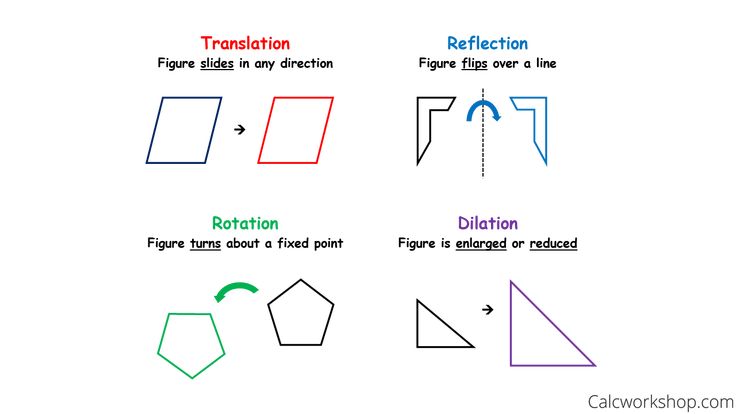 Если
Если y не указан, предполагается, что он равен 0 .
Другими словами:
xnew = xold +новый = старый + <у>
Пример
html,
тело,
свг {
высота: 100%;
}
Scale
Функция преобразования scale( задает операцию масштабирования на x и y . Если y не указано, предполагается, что оно равно x .
Пример
html,
тело,
свг {
высота: 100%;
}
Поворот
Функция преобразования rotate( [ задает поворот на a градусов относительно заданной точки. Если необязательные параметры x и y не указаны, вращение происходит вокруг начала координат текущей пользовательской системы координат. Если заданы необязательные параметры x и y , вращение происходит вокруг точки (x, y) .
Пример
html,
тело,
свг {
высота: 100%;
}
w3.org/2000/svg"> <прямой x="0" у="0" /> <прямоугольник х = "0" у = "0" заполнить = "зеленый" трансформировать = "повернуть (100, 10, 10)" />
SkewX
Функция преобразования skewX() задает преобразование наклона вдоль оси x на - градусов.
Пример
html,
тело,
свг {
высота: 100%;
}
SkewY
Функция преобразования skewY() задает преобразование наклона вдоль оси Y на a градусов.
Пример
html,
тело,
свг {
высота: 100%;
}
| Specification |
|---|
| CSS Transforms Module Level 1 # svg-transform |
| Scalable Vector Graphics (SVG) 2 # TransformProperty |
Found a content problem with эта страница?
- Отредактируйте страницу на GitHub.

- Сообщить о проблеме с содержимым.
- Просмотрите исходный код на GitHub.
Хотите принять участие?
Узнайте, как внести свой вклад.
Последний раз эта страница была изменена участниками MDN.
Основные преобразования — SVG: Масштабируемая векторная графика
- « Предыдущая
- Далее »
Теперь мы готовы начать искажать наши прекрасные изображения. Но сначала давайте официально представим элемент. С помощью этого помощника вы можете назначать свойства полному набору элементов. Собственно, это его единственная цель.
Все последующие преобразования суммируются в атрибуте преобразования элемента. Преобразования можно объединить в цепочку, объединив их, разделив пробелами.
Может потребоваться переместить элемент, даже если вы можете расположить его с соответствующими атрибутами. Для этого translate() Преобразование готово.
В примере будет отображаться прямоугольник, переведенный в точку (30,40) вместо (0,0).
Если второе значение не указано, предполагается, что оно равно 0 .
Вращение элемента — довольно распространенная задача. Используйте для этого преобразование rotate() :
В этом примере показан квадрат, повернутый на 45 градусов. Значение для rotate() указано в градусах.
Преобразования можно легко объединить, просто разделив их пробелами. Например, translate() и rotate() являются широко используемыми преобразованиями.
В этом примере снова показан небольшой квадрат, показанный выше, который на этот раз также повернут на 45 градусов.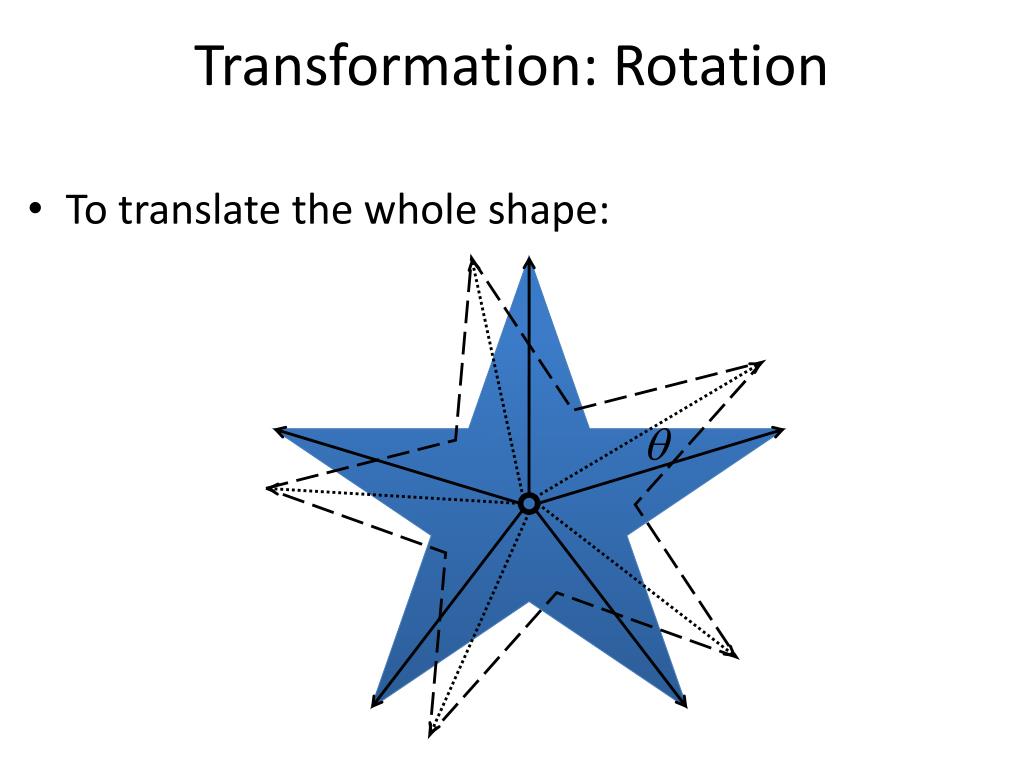
Чтобы сделать из нашего прямоугольника ромб, доступны преобразования skewX() и skewY() . Каждый принимает угол, который определяет, насколько сильно будет перекошен элемент.
scale() изменяет размер элемента. Он принимает два числа, первое из которых представляет собой масштабный коэффициент x , а второе — масштабный коэффициент y . Коэффициенты берутся как отношение преобразованного измерения к исходному. Например, 0,5 сжимается на 50%. Если второе число опущено, оно считается равным первому.
Все вышеуказанные преобразования могут быть выражены матрицей преобразования 2×3. Чтобы объединить несколько преобразований, можно задать результирующую матрицу непосредственно с помощью преобразования matrix(a, b, c, d, e, f) , которое отображает координаты из предыдущей системы координат в новую систему координат по
{xnewCoordSys = axprevCoordSys + cyprevCoordSys + eynewCoordSys = bxprevCoordSys + dyprevCoordSys + f \ left { \ begin {matrix} x * {\ mathrm {prevCoordSys}} = a x * {\ mathrm {newCoordSys}} + c y * {\ mathrm {newCoordSys} } + e \ y * {\ mathrm {prevCoordSys}} = b x * {\ mathrm {newCoordSys}} + d y * {\ mathrm {newCoordSys}} + f \ end {matrix} \right.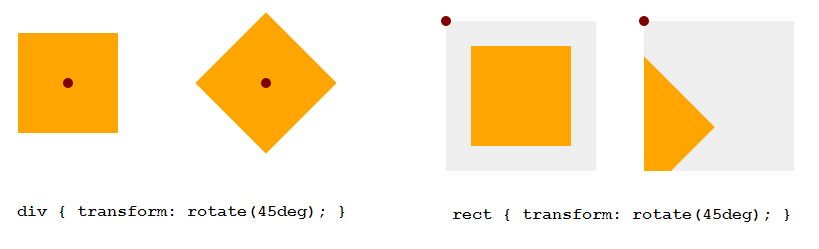
См. конкретный пример в документации по преобразованию SVG. Подробную информацию об этом свойстве можно найти в Рекомендации SVG.
При использовании преобразований вы устанавливаете новую систему координат внутри элемента, к которому применяются преобразования. Это означает, что единицы измерения, которые вы указываете для элемента и его дочерних элементов, могут не соответствовать отображению пикселей 1:1, а также искажаться, искажаться, перемещаться и масштабироваться в соответствии с преобразованием.
Полученный прямоугольник в приведенном выше примере будет иметь размер 100x100px. Более интригующие эффекты возникают, когда вы полагаетесь на такие атрибуты, как userSpaceOnUse и тому подобное.
В отличие от HTML, SVG позволяет легко встраивать другие элементы svg . Таким образом, вы также можете создавать новые системы координат, используя viewBox , width и height внутреннего элемента svg .