Translate transform svg: Трансформации для SVG-элементов — CSS-LIVE — Вебджем.рф

Содержание

НОУ ИНТУИТ | Лекция | Трансформации

Matrix

Трансформация matrix представляет собой способ компактной записи серии преобразований. Графически эта команда не содержит собственных изменений объекта. Она лишь выражает применение одной или нескольких команд типа translation, rotate, scale, skewX и skewY. Математически^{1Если вы видите слово «матрица» в первый раз (одноименный фильм не в счет) – не нужно пугаться. Для начала, что можно сделать – это прочитать лекцию здесь: http://www.intuit.ru/department/mathematics/intmath/11/intmath_11.html
Если вы не до конца поняли этот материал, то ладно, для SVG – графики вы можете просто пользоваться готовыми формулами. Но для понимания почему все же преобразование может быть представлено в виде матрицы, советую обратиться к любому учебнику по линейной алгебре или аналитической геометрии. Превосходное, краткое и ясное изложение я нашел даже в учебнике «Дифференциальное и интегральное исчисления для ВТУЗов» Н.}

С. Пискунов, М., «Наука» 1970, Т2, глава XXI «Матрицы. Матричная запись систем и решений систем линейных дифференциальных уравнений»., все преобразования могут быть выражены в виде матрицы третьего порядка следующим образом:

Команда будет выглядеть так:

matrix(a, b, c, d, e, f)

Каждое из преобразований представляется своей матрицей и соответствующей командой matrix.

Команда translation:

Команда rotate:

Команда scale:

Команда skewX:

Команда skewY:

Практически, для перехода к новой форме записи нужно просто взять исходные параметры команды и аккуратно их подставить в нужные позиции. Для команд rotate, skewX и skewY дополнительно следует вычислить тригонометрические функции углов.

В табл. 6.6 приводятся примеры использования этой записи.

Таблица 6.6. Команда matrix.
№	Код	Вид в браузере
6.6.1	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrix1.svg ( translate1.svg) </desc> <rect x="25" y="25" fill="skyblue" stroke="red" stroke-width="2"/> <rect x="25" y="25" fill="palegreen" stroke="red" stroke-width="2" transform="matrix(1, 0, 0, 1, 100,75)"/> <!-- transform="translate(100,75)--> </svg> Листинг 6. 6.1. Пример matrix1.svg ( translate1.svg)
	Описание
	Запись команды translate в форме matrix.
№	Код	Вид в браузере
6.6.2	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrix2.svg (scale2.svg) </desc> <rect x="25" y="25" fill="skyblue" stroke="red" stroke-width="2"/> <rect x="25" y="50" fill="palegreen" stroke="red" stroke-width="2" transform="matrix(2, 0, 0, 1, 0, 0)"/> <!-- transform="scale(2,1)"--> </svg> Листинг 6. 6.2. Пример matrix2.svg (scale2.svg)
	Описание
	Запись команды scale в форме matrix.
№	Код	Вид в браузере
6.6.3	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrix3.svg (rotate1.svg) </desc> <!--Исходная фигура--> <g> <rect x="105" y="4" fill="yellow" stroke="red" stroke-width="4"/> <rect x="105" y="4" fill="green" stroke="red" stroke-width="4"/> </g> <!--Повернутая фигура--> <g transform="matrix(0. 7071, 0.7071, -0.7071, 0.7071, 0, 0)" > <rect x="105" y="4" fill="yellow" stroke="red" stroke-width="4"/> <rect x="105" y="4" fill="green" stroke="red" stroke-width="4"/> <!-- transform="rotate(45)"--> </g> </svg> Листинг 6.6.3. Пример matrix3.svg (rotate1.svg)
	Описание
	Запись команды rotate в форме matrix.
№	Код	Вид в браузере
6.6.4	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1. 1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrix4.svg (skew1.svg) </desc> <!--Исходная фигура--> <g> <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> </g> <!--Трансформированная фигура --> <g transform="matrix(1, 0, 1, 1, 0, 0)" > <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> <!-- transform="skewX(45)"--> </g> </svg> Листинг 6.6. 4. Пример matrix4.svg (skew1.svg)
	Описание
	Запись команды skewX в форме matrix. tg(45)=1
№	Код	Вид в браузере
6.6.5	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrix5.svg (skew5.svg) </desc> <!--Исходная фигура--> <g> <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> </g> <!--Трансформированная фигура --> <g transform="matrix(1, 1, 0, 1, 0, 0)" > <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> <!-- transform="skewY(45)"--> </g> </svg> Листинг 6. 6.5. Пример matrix5.svg (skew5.svg)
	Описание
	Запись команды skewY в форме matrix. tg(45)=1

Мы разобрали запись в виде матрицы отдельных команд. Немного более сложно обстоят дела с записью нескольких команд, например, translate и skew в виде одной матрицы. Результирующая матрица представляет собой произведение отдельных матриц. Рассмотрим для начала произведение матриц, содержащих по две строки и два столбца:

Обратите внимание на индексы – индекс 12, к примеру, означает, что элемент b

12 находится в первой строке и втором столбце. Результирующая матрица получается сложением и умножением отдельных элементов по следующей схеме (рис. 6.8):

Рис. 6.8. Умножение матриц второго порядка

Аналогичным образом осуществляется умножение матриц третьего порядка:

Для отдельного элемента результирующей матрицы, находящегося во второй строке первого столбца можно выделить схему (рис. 6.9):

Рис. 6.9. Умножение матриц третьего порядка

Итак, для получения результирующей матрицы нескольких команд нужно записать отдельные матрицы, а затем их перемножить. В табл. 6.7 приведены примеры подобных матриц.

Таблица 6.7. Команда matrix для нескольких преобразований.
№	Код	Вид в браузере
6. 7.1	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1"> <title> Лекция 6. Трансформации </title> <desc> Пример matrixGroup1.svg (skew2.svg) </desc> <!--Исходная фигура--> <g> <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> </g> <!--Трансформированная фигура --> <g transform="matrix(1, 0, 1, 1, -6, 0)" > <rect x="10" y="10" fill="yellow" stroke="red" stroke-width="4"/> <rect x="10" y="10" fill="green" stroke="red" stroke-width="4"/> </g> <!-- transform="translate(-6,0) skewX(45)"--> </svg> Листинг 6. 7.1. Пример matrixGroup1.svg (skew2.svg)
	Описание
	Преобразование состоит из двух команд. Запишем их отдельные матрицы: translate(-6,0): skewX(45): Вычисляем произведение матриц: tg(45)=1 Результирующая команда: matrix(1,0,1,1,-6,0)
№	Код	Вид в браузере
6.7.2	<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1" viewBox="0 0 1000 950"> <title> Лекция 6. Трансформации </title> <desc> Пример matrixGroup2. svg (skew7.svg) </desc> <circle cx="500" cy="400" r="300" fill="lightskyblue" stroke="blue" stroke-width="30"/> <ellipse cx="500" cy="500" rx="150" ry="100" fill="none" stroke="blue" stroke-width="30"/> <rect x="300" y="370" fill="lightskyblue"/> <ellipse cx="350" cy="300" rx="100" ry="50" fill="white" stroke="blue" stroke-width="30"/> <ellipse cx="650" cy="300" rx="100" ry="50" fill="white" stroke="blue" stroke-width="30"/> <circle cx="350" cy="300" r="25" fill="black"/> <circle cx="650" cy="300" r="25" fill="black"/> <g transform="matrix(1.3640, 1, 0.3640, 1, -645.6, -400)"> <!-- transform="translate(-500,0) skewX(20) translate(0, -400) skewY(45)"--> <circle cx="500" cy="400" r="300" fill="lightskyblue" stroke="blue" stroke-width="30"/> <ellipse cx="500" cy="500" rx="150" ry="100" fill="none" stroke="blue" stroke-width="30"/> <rect x="300" y="370" fill="lightskyblue"/> <ellipse cx="350" cy="300" rx="100" ry="50" fill="white" stroke="blue" stroke-width="30"/> <ellipse cx="650" cy="300" rx="100" ry="50" fill="white" stroke="blue" stroke-width="30"/> <circle cx="350" cy="300" r="25" fill="black"/> <circle cx="650" cy="300" r="25" fill="black"/> </g> </svg> Листинг 6. 7.2. Пример matrixGroup2.svg (skew7.svg)
	Описание
	Преобразование состоит из четырех команд. Запишем их отдельные матрицы: translate(-500, 0): skewX(20): translate(0, -400): skewY(45): Результирующая матрица будет представлять собой произведение четырех матриц: Вычисляем произведение первых двух матриц: Умножаем результат на третью матрицу: Наконец, результат умножаем на четвертую матрицу: tg(45)=1, tg(20) = 0.3640 Результирующая команда: matrix(1.3640,1,0.3640,1,-645.6,-400)

Запись серии команд в виде матрицы позволяет сократить запись и, следовательно, уменьшить размер SVG – документа.

Вычисление матриц в программе Mathcad

Основная сложность применения команды matrix – это вычисление произведения матриц, представляющее собой довольно трудоемкую и кропотливую задачу. Пакет Mathcad (http://www.ptc.com/go/mathsoft) – мощное средство для решения широкого класса вычислительных задач, содержит удобные инструменты для работы с матрицами. После установки и запуска программы можно сразу приступать к вычислениям. В главном меню выбираем «Insert – Matrix» ( или нажимаем Ctrl+M) (рис. 6.10):

Рис. 6.10. Вставка матрицы

В появившемся диалоговом окне выбираем матрицы размером 3х3 (рис. 6.11):

Рис. 6.11. Определение размера матрицы

В документе появляется шаблон, в который можно вводить числа (рис. 6.12):

Рис. 6.12. Шаблон матрицы

После завершения ввода вводим знак равенства «=» и программа автоматически отображает результирующую матрицу (рис. 6.13):

Рис. 6.13. Готовые матрицы

Программа поддерживает также вычисление тригонометрических функций, которые можно задавать непосредственно в текстовом виде.

SVG — Преобразование перевода | Свг | Датакадамиа

Содержание

SVG — трансформация Translate
- О нас
- Статьи по теме
- Синтаксис
- Пример
- Документация/справка

О

Синтаксис

 перевести( [])

Если Y не указан, предполагается, что он равен нулю.

Это эквивалентно матрице (1 0 0 1 X Y) . то есть

<МАТЕМАТИКА> \begin{bматрица} Икс’ \\ у’\\ 1 \end{bmatrix} знак равно \begin{bmatrix} 1 & 0 & X \\ 0 и 1 и Y \\ 0 и 0 и 1 \end{bmatrix} \begin{bmatrix} Икс \\ у \\ 1 \end{bmatrix}

См. SVG — атрибут преобразования

Пример

NI буквы из прямоугольника

 прямоугольник {
   высота: 20 пикселей;
   ширина: 20 пикселей;
   заполнить:#ECDCC6;
}

Свг

Выход:

Визуализация WebCode

Документация / Справочник

https://developer. mozilla.org/en-US/docs/Web/SVG/Attribute/transform

Геометрия — перевод (дополнение)

Геометрия — перевод (дополнение) О Трансляция — это особый тип матрицы преобразования. Статьи по теме Умножение матриц Видеть . Функциональная форма становится: Пример В Свг,т»…

Геометрия — Перекос (Сдвиг)

Сдвиг — это преобразование, которое поворачивает одну ось так, что оси перестают быть перпендикулярными. Это означает смещение координат по одной или двум осям в зависимости от расстояния по оставшейся оси. Unde «…

SVG — атрибут преобразования

Матрица преобразования в SVG. Основная функция — это матричная функция. Другие, такие как перевод, являются просто ярлыками. …

SVG — View Box

Атрибут Viewbox указывает: граничный блок, в котором видны только внутренние элементы.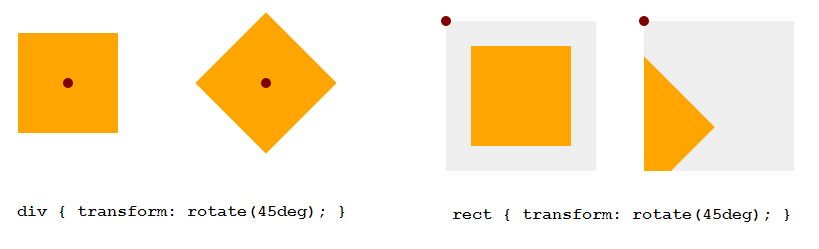 и как изменить размер / подогнать его содержимое при изменении области просмотра. Область просмотра SVG Синтаксис Спецификация viewBox «…

Поделиться этой страницей:

Подписывайтесь на нас:

Преобразование SVG: перевод, масштабирование, поворот

преобразование перевод

Der Wert von transform ist die gewünschte Transformation – z.B. перевести(х у) mit einem oder zwei Werten, die horizontales und vertikales Verschieben bewirken: x entlang der X-Achse, y entlang der y-Achse.

Wenn перевести nur entlang der x-Achse durchgeführt werden soll, reicht der x-Wert. Um auch die Position auf der y-Achse zu ändern, werden beide Werte x und y aufgeführt.

перевести (x (y)): Verschieben entlang der x/y-Achse. x und y werden entweder durch Leerzeichen oder durch Komma getrennt.
повернуть (a (x (y))): Rotieren um einen Winkel a. Die optionalen Parameter x und y versetzen den Punkt, um den das Element rotiert wird.
шкала (x (y)): Verkleinern (mit Werte < 0) bzw. Vergrößern (mit Werten > 0) auf der xy-Achse.
Верте (-1 1) bzw. (1 -1) spiegeln das Element an der x- bzw. у-ахсе. Zwei Werte werden entweder Durch Leerzeichen oder ein Komma getrennt.
skewX(x) skewY(y): Verzerren oder Neigen entlang der xy-Achse

SVG Нульпункт

Он не может быть включен в систему управления операциями Nullpunkt des aktuellen Koordinatensystems (ссылки ViewBox-Ecke oben, если элемент не имеет собственных собственных систем координат во время изменения изменения операционной системы).

SVG-Elemente werden nicht um ihren Mittelpunkt transformiert, sondern um den Ursprung des SVG-Koordinatensystems.

Bei einer Rotation von ~70° verschwindet der Scherenarm. Vergrößern und Verkleinern versetzt das Element in der x/y-Achse.

<использовать xlink:href="#schere" transform="rotate(72)" />

Шкала SVG-элементов – verkleinern und vergrößern

 6)"/>

Schuld ist der Nullpointt, in diesem einfachen Beispiel der Nullpointt der ViewBox.

Нулевой пункт verschieben

Transform-Operationen gehen zunächst vom Nullpointt des aktuellen Koordinatensystems des Elements aus – das ist bei Operationen wie rotate und scale erst einmal nicht тааак интуитивно понятен.

transform = rotate (a, x, y) hat zwei weitere optionale Parameter: x und y sind der Pivotoder Dreh- und Angelpointt und geben dem Element ein eigenes Koordinatensystem.

Die Kommas in transform = rotate(a, x, y) kann man ebensogut weglassen und transform = rotate(a x y) schreiben.

Ähnlich verlaufen die Transformationen auch beim HTML-Canvas, auch dort ist das Äquivalent zum ViewPort, der Context, nur der sichtbare Ausschnitt der Zeichenfläche und ebenfalls der viertel Quadrant. Ну wird beim HTML-Canvas bei Transformationen der gesamte Kontext convertiert und muss anschließen zurückgesetzt werden.

SVG Spiegeln в масштабе

Wenn Elemente со шкалой (-1 1) или шкалой (1 -1) и x- bzw. y-Achse gespiegelt werden, verschwinden sie aus der ViewBox.

Преобразование zweite Transformation translate(x y) verse das Element wieder in the Viewbox.

Преобразование SVG с перекосом

skew(s _x ° s _y °) verzerrt ein Element entlang der x / y-Achse, z.B., um eine andere Perspektive zu bieten oder einen Schatten zu simulieren. Analog wie eine Rotation ist Ausgangspunkt der Verzerrung der Nullpointt der ViewBox.

Der Schatten der Giesskanne entsteht durch skewX, wird durch scale entlang der y-Achse verkürzt und mit convert under das Element geschoben.

Mehrere Transformationen Kombinieren

Alle Operationen können als Liste im transform-Attribut sitzen und werden von rechts nach links ausgeführt. Wie bei CSS: Был zuletzt kommt, солод zuerst. Schließlich könnte man die Transformationen auch verschachtelt anwenden:

Der Untere Scherenarm ist mit scale (1 -1) an der x-Achse gespiegelt und würde außerhalb des sichtbaren Ausschnitts der Viewbox liegen.

шкала (1-1) spiegelt den Scherenarm и x-Achse
translate(0 764) verschiebt das Element / die Gruppe zurück in die ViewBox
rotate(-15 620 380) dreht den Arm um 15° um den Punkt x=620 y=380

                                                             1. Шпигельн ---+
                                         2. Verschieben ---+ |
                           3. Ротьерен ---+ | |
                                          | | |

…

Матрица трансформации матрицы

Wenn Elemente rotiert und skaliert und verschoben werden, kann SVG die langatmige Liste der Operationen durch eine Matrix mit nur 6 Werten ersetzen. Все действия, связанные с 3 x 3-Matrix übergeben werden.

Verschieben mit translate(x y) является эквивалентом матрицы (1 0 0 1 x y).

[10x01y001]

Rotieren mit rotate(a) является эквивалентом матрицы (cos(a) sin(a) -sin(a) cos(a) 0 0). Vor der Transformation müssen die Werte für sin(a) und cos(a) eingesetzt werden.

[cos(a)-sin(a)0sin(a)cos(a)0001]

Eine Rotation rotate(a, cx, cy) ist die Комбинация aus translate(-cx, cy), rotate(a) и Translation zurück цу перевод (сх, су)

[cos(a)-sin(a)-cx*cos(a)+cy*sin(a)+cxsin(a)cos(a)-cx*sin(a)-cy*cos(a)+cy001]

Шкала с масштабом (x y) эквивалентна матрице (x 0 0 y 0 0).

[x000y0001]

Neigen oder Verzerren mit skewX (a) является эквивалентной матрицей (1 0 tan(a) 1 0 0).

[1tan(a)0010001]

Neigen oder Verzerren mit skewY (a) является эквивалентной матрицей (1 tan(a) 0 1 0 0).

[100tan(a)10001]

Der matrix-Parameter braucht nur die ersten 6 Werte.

Translate transform svg: Трансформации для SVG-элементов — CSS-LIVE

НОУ ИНТУИТ | Лекция | Трансформации

Matrix

Вычисление матриц в программе Mathcad

SVG — Преобразование перевода | Свг | Датакадамиа

Содержание

О

Синтаксис

Пример

Документация / Справочник

Рекомендуемые страницы

Геометрия — перевод (дополнение)

Геометрия — Перекос (Сдвиг)

SVG — атрибут преобразования

SVG — View Box

Преобразование SVG: перевод, масштабирование, поворот

преобразование перевод

SVG Нульпункт

Нулевой пункт verschieben

SVG Spiegeln в масштабе

Преобразование SVG с перекосом

Mehrere Transformationen Kombinieren

Матрица трансформации матрицы

Добавить комментарий Отменить ответ

Рубрики