Высота это h – Высота треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Leave a Comment / Разное / By /

Содержание

Высота — Википедия

Материал из Википедии — свободной энциклопедии

Измерения:
L — длина,
B — ширина,
H — высота

Высота́ — измерение объекта или его местоположения, отмеряемое в вертикальном направлении.

В толковом словаре Ушакова определена как «протяжение снизу вверх, вышина»[1].

Расстояние до предмета или точки по вертикали[править | править код]

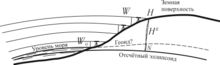Высота земной поверхности над уровнем моря

Строительные сооружения, у которых высота значительно превышает оба других измерения, называются высотными сооружениями и разделяются на башенный и мачтовый типы.

Безопасная высота на производстве — одно из понятий техники безопасности. Если неограждённый перилами перепад горизонтальных поверхностей превышает безопасную высоту, то проведение работ требует выполнения дополнительных условий, как то: медицинский допуск и применение специального снаряжения.

  1. ↑ Толковый словарь русского языка Ушакова // Высота
  2. ↑ Барометрическая высота
  3. ↑ Гл. ред. А. М. Прохоров. Большая Советская Энциклопедия. — 3. — М.: Советская Энциклопедия, 1971. — С. 543. — 640 с.

Высота треугольника — Википедия

Материал из Википедии — свободной энциклопедии

Высота в треугольниках различного типа

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.

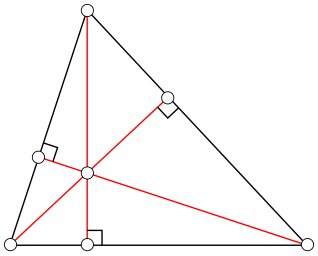Высоты треугольника
  • Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:
EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}

(Для доказательства тождества следует воспользоваться формулами

AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}

В качестве точки E следует взять пересечение двух высот треугольника.)

  • Ортоцентр изогонально сопряжен центру описанной окружности.
  • Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
  • Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
  • Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
  • Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
  • Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
  • Точки, симметричные
    ортоцентру     треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
  • Если О — центр описанной окружности ΔABC, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
    • |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
  • Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
  • Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
  • Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
  • Следствия теоремы Гамильтона:
    • Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
    • Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
  • В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.

Свойства высот равнобедренного треугольника[править | править код]

  • Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
  • Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
  • У равностороннего треугольника все три высоты равны.

Свойства оснований высот треугольника[править | править код]

  • Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
  • Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
  • Другая формулировка последнего свойства:
    • Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
  • Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
  • Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.

Свойства минимальной из высот треугольника[править | править код]

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

  • Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
  • Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
  • При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
  • Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
  • ha=bsin⁡γ=csin⁡β,{\displaystyle h_{a}=b\sin \gamma =c\sin \beta ,}
  • ha=2Sa,{\displaystyle h_{a}={\frac {2S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
  • ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
  • ha=bc2R,{\displaystyle h_{a}={\frac {bc}{2R}},} где bc{\displaystyle bc} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
  • ha:hb:hc=1a:1b:1c=bc:ac:ab{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab}
  • 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}, где r{\displaystyle r} — радиус вписанной окружности.
  • S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}, где S{\displaystyle S} — площадь треугольника.
  • a=2ha⋅(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}}, a{\displaystyle a} — сторона треугольника к которой опускается высота ha{\displaystyle h_{a}}.
  • Высота равнобедренного треугольника, опущенная на основание:
    hc=124a2−c2,{\displaystyle h_{c}={\frac {1}{2}}{\sqrt {4a^{2}-c^{2}}},}
где c{\displaystyle c} — основание, a{\displaystyle a} — боковая сторона.
  • h=32a{\displaystyle h={\frac {\sqrt {3}}{2}}a} — высота в равностороннем треугольнике со стороной a{\displaystyle a}.

Теорема о высоте прямоугольного треугольника[править | править код]

Если высота в прямоугольном треугольнике ABC{\displaystyle ABC} длиной h{\displaystyle h}, проведённая из вершины прямого угла, делит гипотенузу длиной c{\displaystyle c} на отрезки m{\displaystyle m} и n{\displaystyle n}, соответствующие катетам b{\displaystyle b} и a{\displaystyle a}, то верны следующие равенства:

  • h3=mn{\displaystyle h^{2}=mn}
  • a2=cn{\displaystyle a^{2}=cn}; b2=cm{\displaystyle b^{2}=cm}
  • ch=ab{\displaystyle ch=ab}

См. с. 51, ф. (1.11-4)[2]. Теорема о проекциях: c=acos⁡β+bcos⁡α; a=bcos⁡γ+ccos⁡β; b=ccos⁡α+acos⁡γ{\displaystyle c=a\cos \beta +b\cos \alpha ;\ a=b\cos \gamma +c\cos \beta ;\ b=c\cos \alpha +a\cos \gamma }. Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины C{\displaystyle C}, делит противоположную ей сторону c{\displaystyle c} на две части acos⁡β{\displaystyle a\cos \beta } и bcos⁡α{\displaystyle b\cos \alpha }, считая от вершины A{\displaystyle A} к B{\displaystyle B}.

Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.[3]

Теорема[4]. Пусть ABCD{\displaystyle ABCD} – вписанный четырёхугольник, A1{\displaystyle A_{1}} – основание перпендикуляра (высоты), опущенного из вершины A{\displaystyle A} на диагональ BD{\displaystyle BD}; аналогично определяются точки B1,C1,D1{\displaystyle B_{1},C_{1},D_{1}}. Тогда точки A1,B1,C1,D1{\displaystyle A_{1},B_{1},C_{1},D_{1}} лежат на одной окружности.

  1. ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
  2. ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
  3. ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота» (рус.). Открытый урок. Издательский дом «Первое сентября». Дата обращения 19 июля 2017.
  4. ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.

Все формулы высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

 

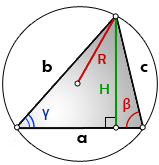Найти длину высоты треугольникаH — высота треугольника

a — сторона, основание

b, c — стороны

β, γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

 

Формула длины высоты через стороны, (H):

Формула длины высоты через стороны

 

 

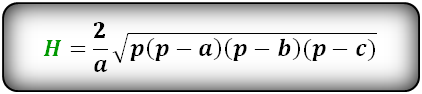
Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и угол

 

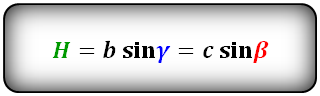
Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через сторону и площадь

 

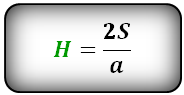
Формула длины высоты через стороны и радиус, (H):

Формула длины высоты через стороны и радиус

 

 

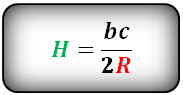
Подробности
Автор: Administrator logo

Ускорение свободного падения — Википедия

Ускоре́ние свобо́дного паде́ния на пове́рхности[1] некоторых небесных тел, м/с2 и g
Земля9,81 м/с21,00 gСолнце273,1 м/с227,85 g
Луна1,62 м/с20,165 gМеркурий3,68—3,74 м/с
2		0,375—0,381 g
Венера8,88 м/с20,906 gМарс3,86 м/с20,394 g
Юпитер23,95 м/с22,442 gСатурн10,44 м/с21,065 g
Уран8,86 м/с20,903 gНептун11,09 м/с21,131 g

Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил. В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2]ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.

Ускорение свободного падения на поверхности Земли

g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет g = 9,80666 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или, грубо, 10 м/с².

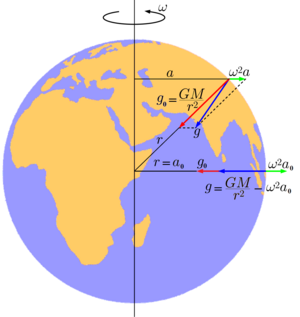Две компоненты ускорения свободного падения на Земле g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна GM/r2 и центробежная, равная ω2a, где
a — расстояние до земной оси, ω — угловая скорость вращения Земли.

Для определённости будем считать, что речь идёт об ускорении свободного падения на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центростремительного ускорения, связанного с вращением Земли.

Центростремительное ускорение[править | править код]

Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, центростремительное ускорение равно ω2a, где ω — угловая скорость вращения Земли, определяемая выражением ω = 2π/T, в котором Т — время одного оборота вокруг своей оси (звёздные сутки), равное для Земли 86164 секунды. Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с

2, причем на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.

Гравитационное ускорение[править | править код]

Гравитационное ускорение на различной высоте h над уровнем моря
h, кмg, м/с2h, кмg, м/с2
09,8066209,7452
19,8036509,6542
29,8005809,5644
39,79741009,505
49,79431209,447
5		9,79125008,45
69,788210007,36
89,782010 0001,50
109,775950 0000,125
159,7605400 0000,0025

В соответствии с законом всемирного тяготения, величина гравитационного ускорения вызванного космическим телом, связано с его массой M следующим соотношением:

g=GMR2{\displaystyle g=G{\frac {M}{R^{2}}}},

где G — гравитационная постоянная (6,67408(31)·10−11м3·с−2·кг−1)[6], а R — растояние от центра гравитации. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо наоборот по известной массе и радиусу определить ускорение свободного падения на поверхности.

Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.

Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:

g(h)=GM(r+h)2{\displaystyle g(h)=G{\frac {M}{(r+h)^{2}}}},
где M — масса планеты, а r — её радиус .

Ускорение свободного падения на Земле[править | править код]

Ускорение свободного падения у поверхности Земли зависит от широты, времени суток, атмосферного давления и других факторов. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:

g=9,780318(1+0,005302sin2⁡φ−0,000006sin2⁡2φ)−0,000003086h,{\displaystyle g=9{,}780318(1+0{,}005302\sin ^{2}\varphi -0{,}000006\sin ^{2}2\varphi )-0{,}000003086h,}
где φ{\displaystyle \varphi } — широта рассматриваемого места,
h{\displaystyle h} — высота над уровнем моря в метрах.

Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли, дополнив её поправками, связанными с вращением Земли, приливными воздействиями и другими факторами.

Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.

Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счет центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от следствий из этой упрощённой модели. Так, самое низкое значение g зафиксировано на горе Уаскаран в Перу (9,7639 м/с²) в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от северного полюса[9].

Ускорение свободного падения для некоторых городов
ГородДолготаШиротаВысота над уровнем моря, мУскорение свободного падения, м/с2
Алматы76,85 в.д.43,22 с.ш.7869.78125
Берлин13,40 в.д.52,50 с.ш.409,81280
Будапешт19,06 в.д.47,48 с.ш.1089,80852
Вашингтон77,01 з.д.38,89 с.ш.149,80188
Вена16,36 в.д.48,21 с.ш.1839,80860
Владивосток131,53 в.д.43,06 с.ш.509,80424
Гринвич0,0 в.д.51,48 с.ш.489,81188
Каир31,28 в.д.30,07 с.ш.309,79317
Киев30,30 в.д.50,27 с.ш.1799,81054
Мадрид3,69 в.д.40,41 с.ш.6679,79981
Минск27,55 в.д.53,92 с.ш.2209,81347
Москва37,61 в.д.55,75 с.ш.1519,8154
Нью-Йорк73,96 з.д.40,81 с.ш.389,80247
Одесса30,73 в.д.46,47 с.ш.549.80735
Осло10,72 в.д.59,91 с.ш.289,81927
Париж2,34 в.д.48,84 с.ш.619,80943
Прага14,39 в.д.50,09 с.ш.2979,81014
Рим12,99 в.д.41,54 с.ш.379,80312
Стокгольм18,06 в.д.59,34 с.ш.459,81843
Токио139,80 в.д.35,71 с.ш.189,79801

Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.

Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.

  • Енохович А. С. Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.

Ортометрическая высота — Википедия

Материал из Википедии — свободной энциклопедии

Ортометрическая высота (система ортометрических высот) — одна из систем высот «над уровнем моря». Ортометрическая высота Hg{\displaystyle H^{g}} имеет определённый физический смысл — длина силовой линии поля силы тяжести от геоида до поверхности Земли [1].

Orthometric Height.png


По свидетельству Лаллемана [2], полковник Шарль Гулье (Charles Moyse Goulier) предложил называть высоту над геоидом в линейной мере l’altitude orthométrique (греч. ορθομετρικό ύψος).

По аналогии с выражением для нормальной высоты, выражение для ортометрической высоты Hg{\displaystyle H^{g}} имеет вид [3]:

Hg=1gm∫0Hgdh,{\displaystyle H^{g}={\frac {1}{g^{m}}}\int _{0}^{H}gdh,}

где среднее интегральное значение реальной силы тяжести gm{\displaystyle g^{m}} должно быть вычислено вдоль силовой линии реального поля от геоида (точка N{\displaystyle N}) до земной поверхности (точка с геодезической высотой H{\displaystyle H}):

gm=1Hg∫NHgdh.{\displaystyle g^{m}={\frac {1}{H^{g}}}\int _{N}^{H}gdh.}

При этом практически получить ортометрическую высоту из геопотенциального числа W0−W=∫0Hgdh=∫NHgdh{\displaystyle W_{0}-W=\int _{0}^{H}gdh=\int _{N}^{H}gdh} затруднительно по двум причинам: для определения среднего интегрального значения gm{\displaystyle g^{m}} на протяжении силовой линии требуется знать хотя бы первые производные реальной силы тяжести (или распределение плотности масс) вплоть до поверхности геоида, также неизвестной. Интегралы ∫0Hgdh=∫NHgdh{\displaystyle \int _{0}^{H}gdh=\int _{N}^{H}gdh} равны, но вычисляются по разному пути: первый — вдоль линии нивелирования от исходного пункта с потенциалом W0{\displaystyle W_{0}}, второй — вдоль силовой линии реального поля.

Для допустимой ошибки определения среднего интегрального значения силы тяжести gm{\displaystyle g^{m}} имеем:

Δgm=ΔHgHggm,{\displaystyle \Delta g^{m}={\frac {\Delta H^{g}}{H^{g}}}g^{m},}

т. е. для определения ортометрической высоты Hg=1{\displaystyle H^{g}=1} км с точностью 1 см требуется знать среднее gm{\displaystyle g^{m}} с точностью 10 мГал, и допуски уменьшаются пропорционально росту высоты [4].

В связи с этим в каталогах ортометрических высот следует обязательно указывать значение gm{\displaystyle g^{m}} для возврата к геопотенциальным числам и последующего преобразования в систему нормальных высот:

Hγ=gmγmHg.{\displaystyle H^{\gamma }={\frac {g^{m}}{\gamma ^{m}}}H^{g}.}

Приближённый способ Гельмерта вывода ортометрических высот приводит к результатам, близким к нормальным высотам [5].

Страны, использующие ортометрическую систему высот до настоящего времени, указаны на карте.

В 1952 г. в СССР прекращено вычисление приближенных значений ортометрических высот и нормальные высоты приняты официально [6].

На территории США сила тяжести на севере на 0,1 % больше, чем на юге, поэтому горизонтальная (уровенная) поверхность, имеющая ортометрическую высоту 1000 м в Монтане, будет иметь высоту в 1001 м в Техасе.

  • ↑ Мещерский И. Н., Ильин А. С., Крюков Ю. А. Нивелирование I и II классов (практическое руководство). — ГУГК. — Москва: Недра, 1982. — 264 с.
  • ↑ Lallemand Ch. Note sur la théorie du nivellement. — Annales des ponts et chausses. — 1887. — С. 491—521.
  • ↑ Еремеев В. Ф. Теория ортометрических, динамических и нормальных высот. — Труды ЦНИИГАиК, вып. 86. — Москва: Геодезиздат, 1951. — С. 11-51.
  • ↑ Юркина М. И. ЦНИИГАиК и теория фигуры Земли (рус.) // Геодезия и картография : журнал. — 1998. — Сентябрь (№ 9). — С. 50—53. — ISSN 0016-7126.
  • ↑ Юркина М. И. К 150-летию Ф. Р. Гельмерта (рус.) // Геодезия и картография : журнал. — 1993. — Ноябрь (№ 11). — С. 59—60. — ISSN 0016-7126.
  • ↑ Еремеев В. Ф. Несколько замечаний о вычислении нивелирных высот в зарубежных странах (рус.) // Геодезия и картография : журнал. — 1964. — Январь (№ 1). — С. 52—60.

    • Высота над уровнем моря — Википедия

    Материал из Википедии — свободной энциклопедии

    Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2019; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2019; проверки требуют 6 правок.

    Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте). В исходном пункте высота принимается равной нулю.

    Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

    Следует отличать следующие понятия:

    • высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
    • высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (т. е. вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

    История понятия

    К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов [1], следуя французскому академику Л. Пюиссану [2][3] отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. [4] Лаплас [5] дал описание астрономической и земной рефракции и измерение высоты барометром.

    Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд [6], Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта [7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

    В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля [8]. Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. [9]

    Основные системы высот над уровнем моря

    1. Динамическая высота (перевод разности потенциалов на линейную меру делением на постоянную величину, близкую к средней силе тяжести, например, среднее значение нормальной силы тяжести на широте 45°). Динамические высоты удобно применять вблизи одной и той же уровенной поверхности замкнутого водоёма или гидротехнического сооружения, в этом случае измеренные превышения не будут отличаться от соответствующей разности динамических высот. Применение динамических высот для решения геодезических задач неудобно, поскольку потребуется вводить поправку за переход к динамическим даже в линии нивелирования низкой точности.
    2. Ортометрическая высота (отрезок силовой линии реального поля силы тяжести от геоида Брунса до точки земной поверхности; разность потенциалов переводится в линейную меру делением на среднее интегральное значение реальной силы тяжести вдоль этого отрезка). Приращения ортометрической высоты по вертикали в точности равны приращению длины.
    3. Нормальная высота (отрезок силовой линии нормального поля силы тяжести от поверхности уровенного эллипсоида вверх до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка). Отметки нормальных высот, хотя и в общем случае непостоянны для одной и той же уровенной поверхности, лучше характеризуют уровенные поверхности с разными потенциалами, чем ортометрические. Приращения нормальной высоты по вертикали не равны приращению длины и соответствуют затуханию аномального гравитационного поля с высотой.
    4. Нормально-ортометрическая высота (отрезок силовой линии нормального поля силы тяжести от земной поверхности вниз до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка).

    Исходный пункт счёта высот

    В России и в Казахстане высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, зафиксированного отметкой на Кронштадтском футштоке.

    Балтийская система высот

    В России в качестве государственной системы высот используется Балтийская система нормальных высот 1977 года, определенная по результатам уравнивания измерений на пунктах государственной нивелирной сети I и II классов главной высотной основы, выполненного ГУГК СССР в 1977 году. Отсчёт нормальных высот в Балтийской системе нормальных высот 1977 года ведется от нуля Кронштадтского футштока. За нуль Кронштадтского футштока принята горизонтальная черта на медной пластине Тонберга, укрепленной в устое Синего моста через Обводной канал в г. Кронштадте. Отметка горизонтальной черты пластины Тонберга равна 0,000 м. Строго говоря, исходным пунктом служит вековой репер вблизи футштока, связанный с началом счёта высот.

    Примеры

    Высоты горных вершин над уровнем моря определены наклонным визирным лучом из тригонометрическим нивелированием с точностью около 1 м, тогда как геодезическая высота вершины над отсчётным эллипсоидом может быть определена с точностью до 1 см с помощью геодезических ГНСС-приёмников.

    См. также

    Комментарии

    Примечания

    1. ↑ Болотов А. П. Геодезия или руководство к исследованию общего вида Земли, построению карт и производству тригонометрической и топографической съемок и нивелировок. Часть II: проекции карт, нивелирование, топография.. — СПб.: К. Вингебер, 1837. — 445 с.
    2. ↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 1. — Paris: Courcier, 1807. — С. 230.
    3. ↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 2. — Paris: Courcier, 1819. — С. 350.
    4. ↑ Puissant L. Traité de topographie, d’arpentage et de nivellement. — Paris: Courcier, 1807. — 332 с.
    5. ↑ Laplace Pierre-Simon. Traité de Mécanique céleste, t. 4. — 1. — Paris: L’Imprimerie Royale, 1805.
    6. ↑ Wand Th. Die Principien der mathematischen Physik und Potentialtheorie. — Leipzig: B. G. Teubner, 1871. — 184 с.
    7. ↑ F. R. Helmert. Zur Theorie des geometrischen Nivellirens (Deutsch) // Astronomische Nachrichten : журнал. — 1873. — Т. 81, № 19. — С. 298-300. — ISSN 1521-3994.
    8. ↑ Молоденский М. С. Основные вопросы геодезической гравиметрии. — Труды ЦНИИГАиК, вып. 42. — Москва: Геодезиздат, 1945. — 108 с.
    9. ↑ Еремеев В. Ф., Юркина М. И. Теория высот в гравитационном поле Земли. — Труды ЦНИИГАиК, вып. 191. — Москва: Недра, 1972. — 144 с.
    10. ↑ Mount Everest — Peakbagger.com
    11. ↑ BBC Russian — В мире — Китай согласился «приподнять» Эверест на 4 метра

    Источники

    Ссылки

    • Гравиметрия и геодезия (Бровар Б.В., Юркина М.И., Тулин В.А., Спиридонов А.И., Демьянов Г.В., Галаганов О.Н., Родкин М.В., Таранов В.А., Кафтан В.И., Жаров В.Е., Авсюк Ю.Н., Светлосанова З.П., Толчельникова С.А., Пик М.В., Молоденский С.М., Денисов В.И., Мельников В.Н., Измайлов В.П., Карагиоз О.В., Колосницын Н.И., Нейман Ю.М., Бывшев В.А., Гусев Н.А., Баграмянц В.О., Копаев А.В., Сорока А.И., Непоклонов В.Б., Кузнецов Ю.Г., Майоров А.Н., Щеглов С.Н., Медведев П.П., Лебедев С.А., Зуева А.Н., Плешаков Д.И., Дубовской В.Б., Конопихин А.А., Соловьев Ю.Ю., Чуйкова Н.А., Пасынок С.Л., Максимова Т.Г., Казарян С.А., Васин М.Г., Попков Д.И., Леонтьев В.И., Сбитнев А.В., Жильников В.Г., Латышев Д.Д., Четверикова А.А.) М.: Научный мир, 2010, 562 с. ISBN: 978-5-91522-189-4

    Литература

    Геодезическая высота — Википедия

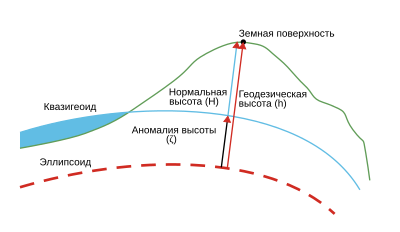    Разница между нормальной, геодезической и высотой квазигеоида

    Геодези́ческой (эллипсоида́льной) высото́й некоторой точки физической поверхности земли называется отрезок нормали к эллипсоиду от его поверхности до данной точки. Вместе с геодезическими широтой и долготой (B и L соответственно) она определяет положение точки относительно заданного эллипсоида. Физически эллипсоида не существует, следовательно геодезическая высота не может быть непосредственно измерена наземными методами. Определить её возможно с помощью спутниковых измерений, а также посредством обработки рядов триангуляции, астрономо-геодезического нивелирования.

    Как видно из определения геодезическая высота зависит от расположения и параметров выбранного эллипсоида, поэтому геодезическую высоту разделяют на две части. Одна из них характеризует физическую поверхность Земли относительно уровенной поверхности (информацию о ней получают в большей степени нивелированием), вторая, более гладкая, характеризует отличие отсчётного эллипсоида от геоида. Первую часть называют гипсометрической, а вторую — гладкой или геоидальной частью. Уровенная поверхность имеет несравненно более плавную форму в сравнении с физической, следовательно геоидальная часть меняется гораздо медленнее гипсометрической.

    В зависимости от особенностей выбора гипсометрической части существуют разные системы геодезических высот:

    Ортометрическая система высот[править | править код]

    Ортометрическая высота точки — это расстояние (H) вдоль отвесной линии от точки до поверхности Геоида. Ортометрическая высота для практических целей является «высотой над уровнем моря».

    Ортометрическая система высот как правило привязанна к определенной высоте в одной точке, а не к точному среднему уровню моря в любом месте.

    Ортометрические высоты обычно используются для инженерных работ, хотя и динамическая высота может быть использованна для крупномасштабных гидрологических целей.

    Альтернативой ортометрической высоте являются динамическая высота и нормальная высота.

    Различные страны используют различные исходные точки опорной поверхности. В России исходным считается Кронштадтский футшток и Балтийская система высот. В США текущий датум NAVD88.

    Поскольку гравитация не является постоянной на больших площадях, ортометрическая высота также не является постоянной. Так на территории США гравитация на 0,1% сильнее на севере Соединенных Штатов, чем на юге, поэтому ровная поверхность, имеющая ортометрическую высоту в 1000 метров в Монтане, будет иметь высоту в 1001 метр в Техасе.

    Нормальная система высот[править | править код]

    Нормальные высоты — это высоты от поверхности квазигеоида, один из нескольких типов высоты. Альтернативы: ортометрическая высота и динамические высоты.

    Нормальная высота точки вычисляется из геопотенциальных чисел путем деления геопотенциального числа точки, т. е. ее разности геопотенциалов с уровнем моря, на среднюю нормальную гравитацию, вычисленную вдоль отвеса точки. (Точнее, вдоль эллипсоидной нормали, усредняя по диапазону высот от 0-эллипсоид-H*; процедура, таким образом, рекурсивна.

    Нормальные высоты, таким образом, зависят от выбранного опорного эллипсоида. Советский Союз и многие другие страны Восточной Европы выбрали высотную систему, основанную на нормальных высотах, определяемых геодезическим точным нивелированием.

    Нормальные значения гравитации легко вычислить через плотность земной коры вокруг отвеса.

    Нормальные высоты занимают видное место в теории гравитационного поля Земли, разработанной школой М. С. Молоденского.

    Эталонная поверхность, с которой измеряются нормальные высоты, называется квазигеоидом, представляющим собой «средний уровень моря», аналогичный геоиду и близкий к нему, но лишенный физической интерпретации эквипотенциальной поверхности.

    Динамическая система высот[править | править код]

    Динамическая высота — это относительный способ указания высоты точки отличной от исходного футштока (глобальной системы высот), в отличие от ортометрической высоты или нормальной высоты. Т.е динамическая высота является локальной.

    Динамическая высота является наиболее подходящей мерой высоты при работе с уровненными поверхностями на большой географической территории и используется Датумом Великих Озер в США и Канаде.

    Динамическая высота постоянна, если следовать одному и тому же гравитационному потенциалу, когда они перемещаются с места на место. Из-за изменения силы тяжести поверхности, имеющие постоянную разницу в динамической высоте, могут быть ближе или дальше друг от друга в различных местах. Динамические высоты обычно выбираются так, чтобы они имели сопряжения с геоидом.

    Когда оптическое выравнивание выполнено, путь близко соответствует следующему значению динамической высоты по горизонтали, но не ортометрической высоте для вертикальных изменений, измеренных на выравнивающем стержне. Таким образом, небольшие поправки должны быть применены к полевым измерениям, чтобы получить либо динамическую высоту, либо ортометрическую высоту, обычно используемую в технике. Паспорта данных Национальной Геодезической службы США дают как динамические, так и ортометрические значения.

    Динамическая высота может быть вычислена с использованием нормальной силы тяжести на 45-градусной широте и геопотенциального числа местоположений.

    • Огородова Л. В. Часть 3. Теоретическая геодезия. // «Высшая геодезия». Учебник для вузов. — Москва: Геодезиздат, 2006. — 384 с. — ISBN 5-86066-076-6.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *