Высота h длина l ширина: Как обозначается ширина длина высота в физике

Содержание

Железобетонные заборы в Нижнем Новгороде

Железобетонные заборы в Нижнем Новгороде — производство, цена невысокая

Заказать звонок

Нужны железобетонные заборы в Нижнем Новгороде? Цена на бетонный забор и столбы ограждений у нас — одна из самых низких в регионе.

ОС-18 [серия 3.017-1]

Длина (L), мм: 1800

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ОС-19 [серия 3.017-1]

Длина (L), мм: 1900

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ОС-24 [серия 3. 017-1]

Длина (L), мм: 2400

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ОС-25[серия 3.017-1]

Длина (L), мм: 2500

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ОС-27 [серия 3.017-1]

Длина (L), мм: 2700

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ОС-30. 1 [серия 3.017-1]

Длина (L), мм: 3000

Ширина (B), мм: 150

Высота (H), мм: 150

Купить в 1 клик

В корзину

ПО-2К(ПБ-4) [ТУ5899-005-050-17.287-99]

Длина (L), мм: 2800

Ширина (B), мм: 2500

Высота (H), мм: 150

Купить в 1 клик

В корзину

СФ3(Ф-3з) [ТУ5899-005-050-17.287-99]

Длина (L), мм: 970

Ширина (B), мм: 970

Высота (H), мм: 450

Купить в 1 клик

В корзину

Предприятие ООО «Арзамасский железобетон» выпускает составные элементы для оград и бетонных заборов в Нижнем Новгороде и Нижегородской области.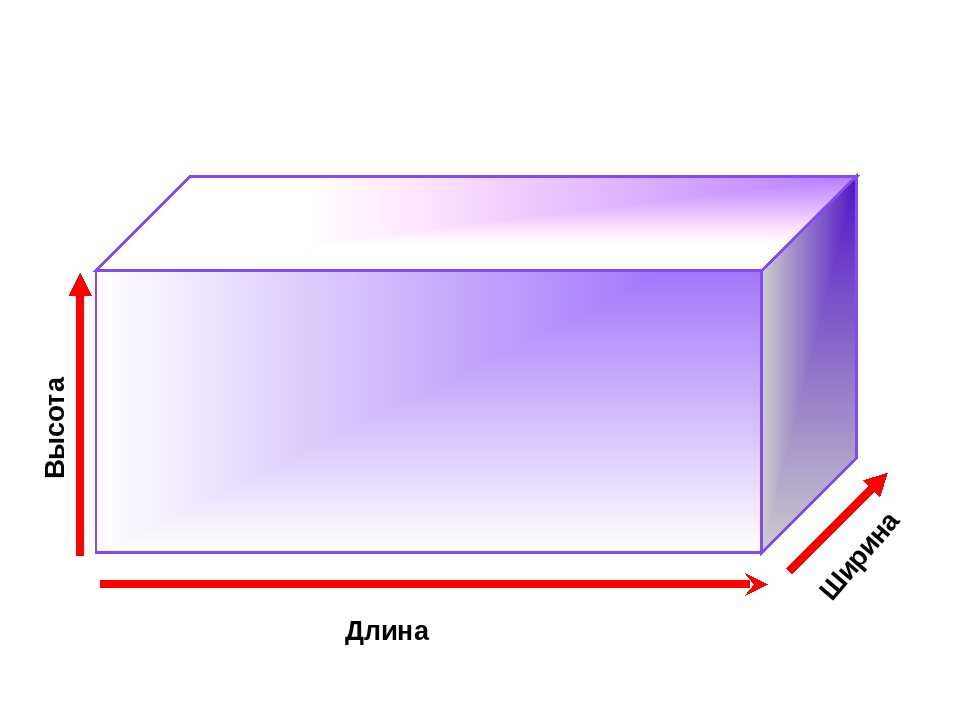 Железобетонные ограждения применяются на промышленных и производственных объектах. Использование армированных конструкций позволяет в несколько раз повысить прочность блоков по сравнению с традиционным кирпичом. Изделия из железобетона устойчивы к неблагоприятным погодным условиям, имеют высокие показатели влаго- и термостойкостью. Это исключает необходимость регулярного обслуживания и ремонта. Они отличаются удобством и быстротой монтажа. Для установки бетонного забора требуется немного времени и рабочей силы.

У нас можно заказать все необходимые элементы железобетонных заборов в Нижнем Новгороде: плиты ограждений, отдельные опорные и монтажные элементы конструкций:

опоры серии 3.017-1:
- ОС-18;
- ОС-19;
- ОС-24;
- ОС-25;
- ОС-27;
- ОС-30.1.
щелевые фундаментные стаканы СФ3;
плиты забора ПО-2К (ПБ-4).

Выпускаемые ЖБИ соответствуют нормам и требованиям, указанным в ТУ5899-005-050-17. 287-99. Отливка производится в специальные формы, обеспечивающие высокую точность размеров. В качестве сырья используется высококачественный бетон повышенной прочности (вплоть до марок В60 и В65). Металлические элементы каркаса подвергаются цинкованию, что повышает их устойчивость к атмосферному воздействию и агрессивным химическим средам. Таким образом гарантированный срок эксплуатации изделий может быть увеличен до 50 лет.

Чтобы купить столбы для забора, бетонные заборы и их элементы в Нижнем Новгороде, свяжитесь с представителями компании или обратитесь по адресам, приведенным на сайте. Оплата производится наличными или банковским переводом на расчетный счет предприятия. На бетонные заборы цена формируется исходя из объема приобретаемых ЖБИ и условий доставки. Для доставки продукции на объект используется собственный автопарк компании. Машины имеют грузоподъемность от 12 до 20 т, что позволяет сократить требуемое для перевозки количество транспорта, сэкономить время и средства заказчика.

JoomShopping Download & Support

Заказать звонок

Длина (L), мм

970

1800

1900

2400

2500

2700

2800

3000

Ширина (B), мм

150

970

2500

Высота (H), мм

150

450

Сбросить

Ваше имя

Ваш номер телефона:

Ваше имя

Ваш номер телефона:

Ваше имя

Ваш номер телефона:

Прогоны в Арзамасе и Н.

Новгороде Прогоны в Арзамасе и Н.Новгороде

Заказать звонок

ПРГ28.1.3.4т [Серия 1.225-2 (вып.12)]

Длина (L), мм: 2780

Ширина (B), мм: 120

Высота (H), мм: 300

Купить в 1 клик

В корзину

ПРГ32.1.4.4т [Серия 1.225-2 (вып.12)]

Длина (L), мм: 3180

Ширина (B), мм: 120

Высота (H), мм: 400

Купить в 1 клик

В корзину

ПРГ36.1.4.4т [Серия 1.225-2 (вып.12)]

Длина (L), мм: 3580

Ширина (B), мм: 120

Высота (H), мм: 400

Купить в 1 клик

В корзину

ПРГ60. 2.5.4т [Серия 1.225-2 (вып.12)]

Длина (L), мм: 5980

Ширина (B), мм: 120

Высота (H), мм: 500

Купить в 1 клик

В корзину

Заказать звонок

Длина (L), мм

2780

3180

3580

5980

Ширина (B), мм

120

200

Высота (H), мм

300

400

500

Сбросить

Ваше имя

Ваш номер телефона:

Ваше имя

Ваш номер телефона:

Ваше имя

Ваш номер телефона:

Творческий проект для классов К-8

Креатив Проекты для К-12

Урок Планы

1869 Задача вступительного теста MIT
Проблема «3N+1»
Корзина, полная яиц
Геометрическое доказательство теоремы Пифагора 9 «вырезать и вставить»0022
Проблема для Молодые и старые ученики
Проблема от русского Математическая олимпиада
Доказательство Пифагора теорема с использованием подобных треугольников
Головоломка с целыми числами от одного до шестнадцати
Головоломка с номером 1089
«Струнный рисунок», который мы можем нарисовать: ромб внутри шестиугольника
Трехсторонний кот для рисования
Путешественник на сетке 6 на 6
Дополнительная плата
Прибавление в детском саду и первый класс
Арифметическое чудо из 1899 года
Старый купец и его четверо детей
Древний узел
Анимации на TI
Углы треугольника: геометрическое свойство посредством складывания бумаги
Районы и границы
Площадь и Периметр
Арифметика с манипуляциями
Средний балл за тест
Мяч в коробке
Банан
Бочки, Бочки и другие фигурные контейнеры
Большие числа АКА Зерна риса на шахматная доска
Блочные дома
Сборка собачьей будки в масштабе
Создание ящика со скелетом в соответствии с к Спецификации
Свечи
Корзины для конфет
Емкость
Наутилус с камерой
Проверка, является ли число простым номер
Коробка с китайским календарем
Хорды по кругу
Круг, квадрат и треугольник
Часы и время
Монеты
Раскрашивание линий в шестиугольнике
Красочный Треугольники
Конгруэнтность Треугольники
Подсчет
Счетная доска для детей учащиеся
Счет до 100
Бумага для биговки По кривым
Кубики
Куб со срезанным краем
Кухня полоски
Вырезание прямоугольника
Вырезание треугольника
Разрезание треугольника на две части куски равной площади и равного периметра
Вырезание равностороннего треугольника
Резка многогранников
Цилиндр и конус одинаковой высоты и диаметра основания
Вывод формулы для площадь треугольника
Диагональ площади
Разделение квадрата
Деление с остатком на ТИ-108: Два экземпляра
Собаки, кошки и мыши
Точка за точкой
Удвоение и деление пополам
Чертеж прямоугольник
Рисование простой фигуры из устных указаний
Рисование треугольников
Легкие квадраты
Яичная дилемма (Часть 1)
Возведение в степень
Факторинг
фантазии Конверты
Нахождение дроби между двумя дроби
Пятиконечный 3D Звезда
переворачивание монеты
Сложенный бумажный цветок С шестью лепестками
Четыре жука
Четыре карты
Четыре кубика
От миллиарда до нуля
От одного до одного триллиона
Игра кругов и звезд
Игра в десятки
Гигантская энчилада
Шапка для Хэллоуина
Орел или решка?
Шестиугольная головоломка
Праздник Орнамент
Лошадь на продажу
Как работает Калькулятор Вычислить квадратный корень из числа?
Сколько пентамино?
Сколько клеток на шахматной доске?
Сколько треугольников? (Части 1 и 2)
Сколько треугольников в этом треугольнике?
Как измерить угол без транспортира
Как превратить прямоугольник в другой прямоугольник
Гиперболы и Эллипсы
Я могу угадать твой возраст!
Я могу угадать ваш возраст и номер дома!
Невозможный объект
Вписанный треугольник
Проценты
Введение в измерения (первый класс)
Неправильные многоугольники
Юлекурв АКА Валентайн Корзина
Прыжок: игра в пасьянс с десятью жетонами
Воздушные змеи
Умножение решетки
Дырявая крыша
Ушастые твари
Волшебные бобы
Волшебный складной кубик
Магический квадрат
Создание животных Режущие полигональные пазлы
Создание блоков из четырех Кубики
Изготовление коробок
Изготовление эвольвенты
Лабиринт
Мини-слот-машина
Луны
Больше задач «точка-точка»
Больше старых словесных задач
Умножения «Готово по Адаму Рису»
Натан подбрасывает монету 20 раз
Игра в числа с Кости
Головоломка с числами
Воля старого пастуха
Олимпийские кольца
Одна треть
Покраска домов (и другие «рабочие» задачи)
Парадокс средних
Разделение квадрата
Пентагон Пазлы
Алгебра телефонных номеров
Копилка
Игра с формами
Powerball 55
Красивая подарочная коробка
Простые числа: сито Эратосфена
Свойства коробки
Тыквы
Пазл с камешками
Пирамида на четверти
Пирамида из кубиков
Пирамида из мрамора
Четырехугольники
Прямоугольники
Правильные многоугольники с равными Районы
Связанные проблемы
Прямоугольный треугольник
Последовательности составных номера: конкурс
Фигуры цифр
Формы чисел с использованием треугольники
Делиться хлебом
Овца: Старая головоломка
Шесть пирамид
Шестнадцать Квадратные дюймы
Печать Соломона
Сортировочная игра
Спираль (марки К-4)
Спираль (5-8 классы)
Спираль Феодора на Калькуляторе ТИ-83/84
Квадратные и кубические единицы
Квадрат в треугольнике
Соломенные многогранники
Алгоритм вычитания
Вычитание со счетчиками
Сумма всех 100 чисел в таблице умножения
Сумма первых N целых чисел
Сумма двух квадратов
Выживший на шестиугольном острове
Татами
Чайные коробки
Преобразование температуры
Мозаика круга
Задача о лестнице и ящике
Сыр «Смеющаяся корова» Клиновые контейнеры
Практическая ценность Доказательства
Рейнберд Зуни
Три четверти
Круг из трех частей Пазл
Бросание одного кубика
Треугольник в квадрат: A шарнирный разборный
Превращение прямоугольника в квадрат путем вскрытия
Двенадцать простых фигур
Двадцать четыре кубика
Две старые проблемы
Два брата-пастуха
Понимание Длинная дивизия
Необычный Контейнеры
Что дальше?
Что это за прямоугольник?
Инь Ян

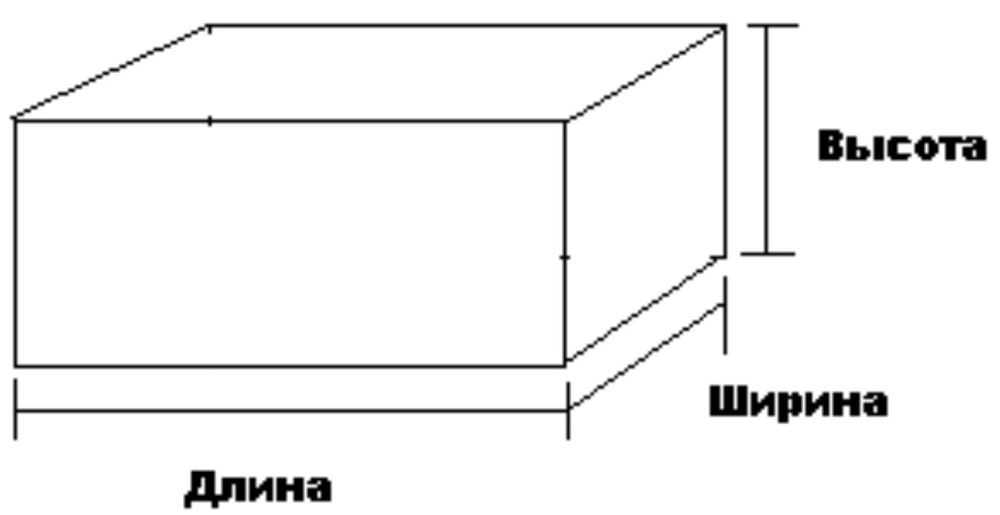
Нахождение объема и площади поверхности прямоугольных тел

Результаты обучения

Нахождение объема и площади поверхности прямоугольного тела

Тренер по группе поддержки заставляет команду раскрасить деревянные ящики школьными цветами, чтобы они стояли на играх. (См. изображение ниже). Количество краски, необходимое для покрытия внешней стороны каждой коробки, представляет собой площадь поверхности, квадратную меру общей площади всех сторон. Объем пространства внутри ящика — это объем, кубическая мера.

Этот деревянный ящик имеет форму прямоугольного тела.

Каждый ящик имеет форму прямоугольного тела. Его размерами являются длина, ширина и высота. Прямоугольное твердое тело, показанное на изображении ниже, имеет длину [латекс]4[/латекс], единицы ширины [латекс]2[/латекс] и высоту [латекс]3[/латекс]. Можете ли вы сказать, сколько всего кубических единиц? Смотрим слой за слоем.

Разбивка прямоугольного твердого тела на слои упрощает визуализацию количества содержащихся в нем кубических единиц. Это [латекс]4[/латекс] на [латекс]2[/латекс] на [латекс]3[/латекс] прямоугольное тело имеет [латекс]24[/латекс] кубических единиц.

Всего [латекс]24[/латекс] кубических единицы. Обратите внимание, что [латекс]24[/латекс] — это [латекс]\текст{длина}\times \text{ширина}\times \text{высота}\текст{.}[/latex]

Объем, [ латекс]V[/латекс] любого прямоугольного твердого тела является произведением длины, ширины и высоты.

[латекс]V=LWH[/латекс]

Мы могли бы также записать формулу объема прямоугольного тела через площадь основания. Площадь основания, [латекс]B[/латекс], равна [латекс]\текст{длина}\раз \текст{ширина}\текст{.}[/латекс]

[латекс]В=L \cdot W[/latex]

Мы можем заменить [latex]B[/latex] на [latex]L\cdot W[/latex] в формуле объема, чтобы получить другую форму формулы объема.

Теперь у нас есть другая версия формулы объема для прямоугольных тел. Давайте посмотрим, как это работает с прямоугольным телом [latex]4\times 2\times 3[/latex], с которого мы начали. См. изображение ниже.

Чтобы найти площадь поверхности прямоугольного тела, подумайте о нахождении площади каждой из его граней. Сколько граней у прямоугольного тела, показанного выше? Вы можете увидеть три из них.

[латекс]\begin{array}{ccccccc}{A}_{\text{front}}=L\times W\hfill & & & {A}_{\text{side}}=L\times W \hfill & & & {A}_{\text{top}}=L\times W\hfill \\ {A}_{\text{front}}=4\cdot 3\hfill & & & {A}_ {\ text {сторона}} = 2 \ cdot 3 \ hfill & & & {A} _ {\ text {верх}} = 4 \ cdot 2 \ hfill \\ {A} _ {\ text {спереди}} = 12 \hfill & & & {A}_{\text{side}}=6\hfill & & & {A}_{\text{top}}=8\hfill \end{массив}[/latex]

Обратите внимание, что для каждого из трех лиц, которые вы видите, есть идентичное противоположное лицо, которое не отображается.

[латекс]\begin{array}{l}S=\left(\text{front}+\text{back}\right)\text{+}\left(\text{left side}+\text{ правая сторона}\справа)+\слева(\текст{сверху}+\текст{снизу}\справа)\\ S=\слева(2\cdot \текст{спереди}\справа)+\слева(\текст{2 }\cdot \text{слева}\справа)+\слева(\text{2}\cdot \text{сверху}\справа)\\ S=2\cdot 12+2\cdot 6+2\cdot 8\ \ S=24+12+16\\ S=52\text{кв. Units}\end{array}[/latex]

Площадь поверхности [latex]S[/latex] прямоугольного тела, показанного выше , составляет [latex]52[/latex] квадратных единиц.
В общем, чтобы найти площадь поверхности прямоугольного тела, помните, что каждая грань является прямоугольником, поэтому ее площадь является произведением ее длины и ширины (см. рисунок ниже). Найдите площадь каждого лица, которое вы видите, а затем умножьте каждую площадь на два, чтобы учесть лицо на противоположной стороне.

[латекс]S=2LH+2LW+2WH[/латекс]

Для каждой грани прямоугольного твердого тела, обращенной к вам, есть другая грань на противоположной стороне. Всего [латексных]6[/латексных] лиц.

Объем и площадь поверхности прямоугольного тела

Для прямоугольного тела длиной [латекс]L[/латекс], шириной [латекс]W[/латекс] и высотой [латекс]Н:[/латекс]

Выполнение Упражнение по манипулятивной математике «Раскрашенный куб» поможет вам лучше понять объем и площадь поверхности.

пример

Для прямоугольного твердого тела длиной [латекс]14[/латекс] см, высотой [латекс]17[/латекс] см и шириной [латекс]9[/латекс] см найдите 1. объем и 2. площадь поверхности.

Решение
Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.

Шаг 1. Прочтите проблему. Нарисуйте фигуру и

пометьте его данной информацией.

1.
Шаг 2. Идентифицируйте то, что вы ищете.	объем прямоугольного тела
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть [латекс]V[/латекс] = объем
Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель.	[латекс]V=LWH[/латекс] [латекс]V=\mathrm{14}\cdot 9\cdot 17[/латекс]
Шаг 5. Решите уравнение.	[латекс]V=2,142[/латекс]
Шаг 6.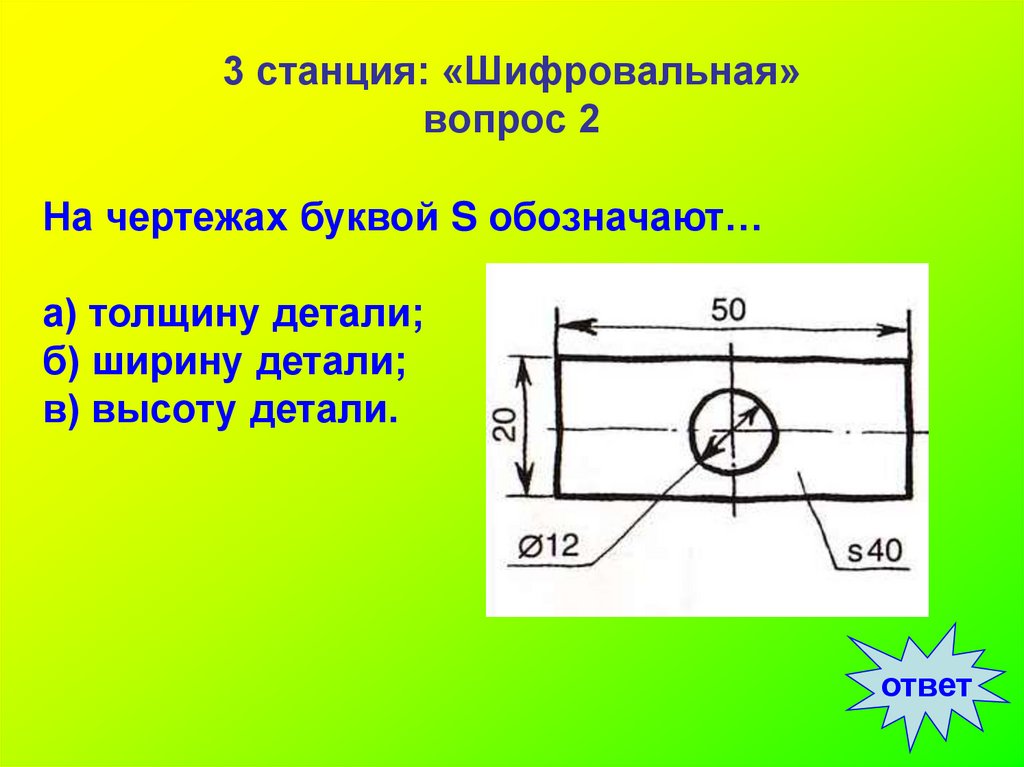 Проверка Мы оставляем вам возможность проверить ваши расчеты.
Шаг 7. Ответьте на вопрос.	Площадь поверхности составляет [латекс]\текст{1,034}[/латекс] квадратных сантиметров.

2.
Шаг 2. Идентифицируйте то, что вы ищете.	площадь поверхности твердого тела
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть [латекс]S[/латекс] = площадь поверхности
Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель.	[латекс]S=2LH+2LW+2WH[/латекс] [латекс]S=2\левый(14\cdot 17\правый)+2\левый(14\cdot 9\правый)+2\левый(9\cdot 17\правый)[/латекс]
Шаг 5. Решите уравнение.	[латекс]S=1,034[/латекс]
Шаг 6. Проверить: Перепроверить с помощью калькулятора.
Шаг 7. Ответьте на вопрос.	Площадь поверхности [латекс]1034[/латекс] квадратных сантиметров.

попробуйте

пример

Прямоугольный ящик имеет длину [латекс]30[/латекс] дюймов, ширину [латекс]25[/латекс] дюймов и высоту [латекс] 20[/латекс] дюймов. Найдите его 1. объем и 2. площадь поверхности.

Показать раствор

попробуй

Куб — прямоугольное тело, длина, ширина и высота которого равны. См. Объем и площадь поверхности куба ниже. Замена, 9{2}[/латекс].

Объем и площадь поверхности куба

Для любого куба со сторонами длиной [латекс]s[/латекс],

пример

Куб имеет [латекс]2,5[/латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности.

Решение
Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.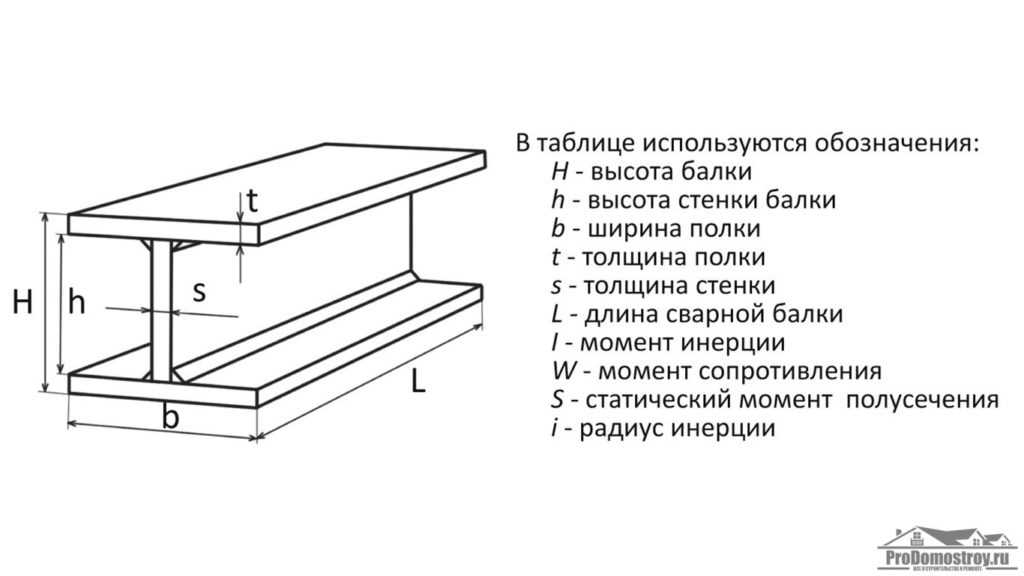

Шаг 1. Прочтите проблему. Нарисуйте фигуру и

пометьте его данной информацией. 9{3}[/латекс]

[латекс]V=15,625[/латекс]

Шаг 6. Проверка: Проверьте свою работу.

Шаг 7. Ответьте на вопрос.

Объем [латекс]15,625[/латекс] кубических дюймов.

2.
Шаг 2. Идентифицируйте то, что вы ищете.	площадь поверхности куба
Шаг 3. Имя. 9{2}[/латекс] [латекс]S=37,5[/латекс]
Шаг 6. Чек: Чек оставлен вам.
Шаг 7. Ответьте на вопрос.	Площадь поверхности [латекс]37,5[/латекс] квадратных дюймов.

попробуйте

пример

Блокнот размером [латекс]2[/латекс] дюйма с каждой стороны.

Железобетонные заборы в Нижнем Новгороде

Прогоны в Арзамасе и Н.

Творческий проект для классов К-8

Нахождение объема и площади поверхности прямоугольных тел

Результаты обучения

Объем и площадь поверхности прямоугольного тела

пример

попробуйте

пример

попробуй

Объем и площадь поверхности куба

пример

попробуйте

пример

Добавить комментарий Отменить ответ

Рубрики