Знак степень 4: Верхний индекс четыре, Номер в Юникоде: U+2074, Надстрочные символы в Разделе: Надстрочные и подстрочные знаки 📖 узнать значение и ✂ скопировать символ (◕‿◕) SYMBL

Степени и возведение в степень, вторая, третья, четвёртая степени

Когда число умножается само на себя, произведение называется степенью.

Так      2.2 = 4, квадрат или вторая степень 2-х
     2.2.2 = 8, куб или третья степень.
     2.2.2.2 = 16, четвёртая степень.

Также,      10.10 = 100, вторая степень 10.
     10.10.10 = 1000, третья степень.
    10.10.10.10 = 10000 четвёртая степень.

И      a.a = aa, вторая степень a
     a.a.a = aaa, третья степень a
     a.a.a.a = aaaa, четвёртая степень a

Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.

Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель

. Это число или буква называется показателем степени или степенью числа. Так, а² равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a³ означает aaa, то есть здесь a повторяется три раза как множитель.

Показатель первой степени есть 1, но он обычно не записывается. Так, a¹ записывается как a.

Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a.      Но a⁴ = a.a.a.a

Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть

некоторой степенью другой величины.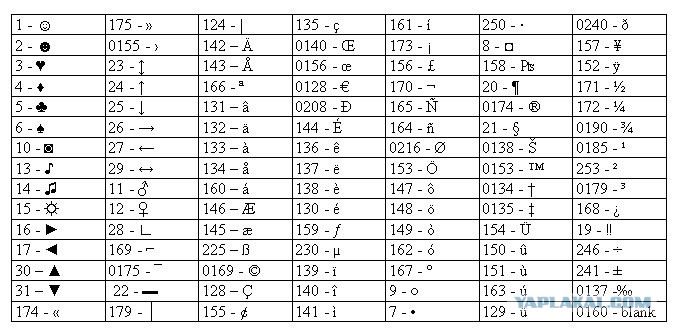 Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a^x, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, b^m и dⁿ возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b^m = b³; но если m = 5, тогда b^m=b⁵.

Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)³ есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a³ + 3a

2b + 3a²d + 3ab² + 6abd + 3ad² + b³ + d³.

Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.

Так, в ряде      aaaaa, aaaa, aaa, aa, a;
или        a⁵, a⁴, a³, a², a¹;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.

Tак a.a = a², второй член. И a³.a = a⁴
     a².a = a³, третий член. a⁴

.a = a⁵.

Если мы начнем слева делить на a,
мы получим a⁵:a = a⁴      и a³:a = a².
a⁴:a = a³       a²:a = a¹

Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.

Так, a:a = a/a = 1. (1/a):a = 1/aa
     1:a = 1/a      (1/aa):a = 1/aaa.

Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.

Или a⁵, a⁴, a³, a², a, 1, 1/a, 1/a², 1/a³.

Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.

Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a

3) = a³.

Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)³, (a + b)², (a + b), 1, 1/(a + b), 1/(a + b)², 1/(a + b)³.

Для удобства используется еще одна форма записи обратных степеней.

Согласно этой форме, 1/a или 1/a¹ = a^-1. И 1/aaa или 1/a³ = a^-3.
1/aa или 1/a² = a^-2. 1/aaaa или 1/a⁴ = a^-4.

А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a⁰.

Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать      a

4, a³, a², a¹, a⁰, a^-1, a^-2, a^-3, a^-4.
Или      a⁺⁴, a⁺³, a⁺², a⁺¹, a⁰, a^-1, a^-2, a^-3, a^-4.

А ряд только отдельно взятых степеней будет иметь вид:
     +4,+3,+2,+1,0,-1,-2,-3,-4.

Корень степени может выражен более чем одной буквой.

Так, aa.aa или (aa)² есть второй степенью aa.
И aa.aa.aa или (aa)³ есть третьей степенью aa.

Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.

Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:

Умножайте величину саму на себя столько раз, сколько указано в степени числа.

Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.

Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.

Четвертая степень a есть a⁴ или aaaa. (Art. 195.)
Шестая степень y есть y⁶ или yyyyyy.
N-ая степень x есть xⁿ или xxx….. n раз повторенное.

Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.

Tак (ay)² =a²y²; (ay)² = ay.ay.
Но ay.ay = ayay = aayy = a²y².
Так, (bmx)³ = bmx.bmx.bmx = bbbmmmxxx = b³m³x³.

Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.

Пример 1. Четвертая степень dhy есть (dhy)⁴, или d⁴h⁴y⁴.

Пример 2. Третья степень 4b, есть (4b)³, или 4³b³, или 64b³.

Пример 3. N-ая степень 6ad есть (6ad)ⁿ или 6ⁿaⁿdⁿ.

Пример 4. Третья степень 3m.2y есть (3m.2y)³, или 27m³.8y³.

Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,

(a + b)¹ = a + b, первая степень.
(a + b)¹ = a² + 2ab + b², вторая степень (a + b).
(a + b)³ = a ³ + 3a²b + 3ab² + b³, третья степень.
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴, четвертая степень.

Квадрат a — b, есть a² — 2ab + b².

3 + 3a² + 3a + 1.

Квадрат a + b + h есть a² + 2ab + 2ah + b² + 2bh + h²

Упражнение 1. Найдите куб a + 2d + 3

Упражнение 2. Найдите четвертую степень b + 2.

Упражнение 3. Найдите пятую степень x + 1.

Упражнение 4. Найдите шестую степень 1 — b.

Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.

Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a² + 2ah + h

2      также, (a — h)(a — h) = a² — 2ah + h².

Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.

Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.

Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.

Пример 1. Квадрат 2a + b, есть 4a² + 4ab + b².

Пример 2. Квадрат ab + cd, есть a²b² + 2abcd + c²d².

Пример 3. Квадрат 3d — h, есть 9d₂ + 6dh + h²

.

Пример 4. Квадрат a — 1 есть a² — 2a + 1.

Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.

Во многих случаях является эффективным записывать степени без умножения.

Так, квадрат a + b, есть (a + b)².
N-ая степень bc + 8 + x есть (bc + 8 + x)ⁿ

В таких случаях, скобки охватывают все члены под степенью.

Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.

Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]² или (a + b)².(c + d)².

Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.

Куб a.(b + d), есть [a.(b + d)]³, или a³.(b + d)³.

Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.

Вторая степень (- a) есть +a²
Третья степень (-a) есть -a³
Четвёртая степень (-a) есть +a⁴
Пятая степень (-a) есть -a⁵

Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a²
И -a.-a = +a²

Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.

Третья степень a² есть a^2.3 = a⁶.

Для a² = aa; куб aa есть aa.aa.aa = aaaaaa = a⁶; что есть шестой степенью a, но третьей степенью a².

Четвертая степень a³b² есть a^3.4b^2.4 = a¹²b⁸

Третья степень 4a²x есть 64a⁶x³.

Пятая степень (a + b)² есть (a + b)¹⁰.

N-ая степень a³ есть a³ⁿ

N-ая степень (x — y)^m есть (x — y)^mn

(a³.b³)² = a⁶.b⁶

(a³b²h⁴)³ = a⁹b⁶h¹²

Правило одинаково применяется к отрицательным степеням.

Пример 1. Третья степень a^-2 есть a^-3.3=a^-6.

Для a^-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a⁶ = a^-6

Четвертая степень a²b^-3 есть a⁸b^-12 или a⁸/b¹².

Квадрат b³x^-1, есть b⁶x^-2.

N-ая cтепень ax^-m есть x^-mn или 1/x.

Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.

Пример 1. Квадрат -a³ есть +a⁶. Квадрат -a³ есть -a³.-a³, которое, согласно правилам знаков при умножении, есть +a⁶.

2. Но куб -a³ есть -a⁹. Для -a³.-a³.-a³ = -a⁹.

3. N-ая степень -a³ есть a³ⁿ.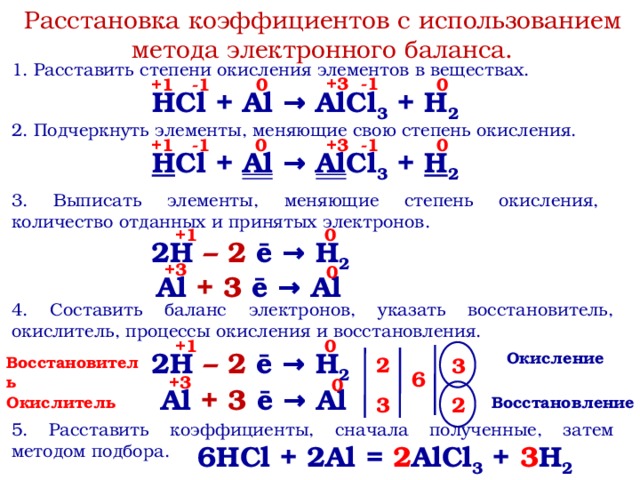

Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.

Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.

Квадрат a/b есть a²/b². Согласно правилу умножению дробей,
     (a/b)(a/b) = aa/bb = a²b²

Вторая, третья и n-ая степени 1/a есть 1/a², 1/a³ и 1/aⁿ.

Примеры двочленов, в которых один из членов является дробью.

1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)² = x² + 2.x.(1/2) + 1/2² = x² + x + 1/4
(x — 1/2)² = x² — 2.x.(1/2) + 1/2² = x² — x + 1/4

2. Квадрат a + 2/3 есть a² + 4a/3 + 4/9.

3. Квадрат x + b/2 = x² + bx + b²/4.

4 Квадрат x — b/m есть x² — 2bx/m + b²/m².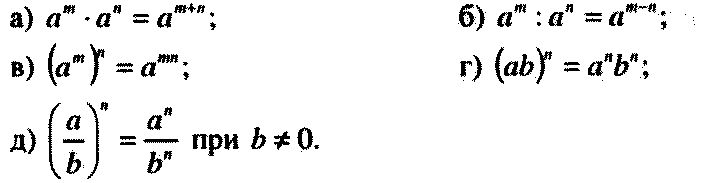

Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.

Так, в дроби ax^-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax_-2/y = (a/y).x^-2 = (a/y).(1/x² = a/yx².

В дроби a/by³ мы можем переместить у из знаменателя в числитель.
Тогда a/by₂ = (a/b).(1/y³) = (a/b).y^-3 = ay^-3/b.

Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.

Так, ax³/b = a/bx^-3. Для x³ обратным есть x_-3, что есть x³ = 1/x^-3.

Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.

Так, a/b = 1/ba^-1, or ab^-1.

§ Что такое степень числа. Степень с натуральным показателем

Что такое степень числа Свойства степени Возведение в степень дроби

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

• 4 — основание степени;
• ⁶ — показатель степени.

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:

Запомните!

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

Запись «aⁿ» читается так: «а в степени n» или «n-ая степень числа a».

Исключение составляют записи:

• a² — её можно произносить как «а в квадрате»;
• a³ — её можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

• a² — «а во второй степени»;
• a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

Запомните!

Степенью числа «а» с показателем n = 1 является само это число:
a¹ = a

Любое число в нулевой степени равно единице.
a⁰ = 1

Ноль в любой натуральной степени равен нулю.
0ⁿ = 0

Единица в любой степени равна 1.
1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишённым смысла.

• (−32)⁰ = 1
• 0²⁵³ = 0
• 1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

• 5³ = 5 · 5 · 5 = 125
• 2,5² = 2,5 · 2,5 = 6,25
• ()⁴ = · · · =

  3 · 3 · 3 · 3

  4 · 4 · 4 · 4

  =

  81

  256

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

Запомните!

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

• 2 · (−3)² = 2 · (−3) · (−3) = 2 · 9 = 18
• −5 · (−2)³ = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5)⁴ и −5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5)⁴ означает найти значение четвёртой степени отрицательного числа.

(−5)⁴ = (−5) · (−5) · (−5) · (−5) = 625

В то время как найти «−5⁴» означает, что пример нужно решать в 2 действия:

1. Возвести в четвёртую степень положительное число 5.
   5⁴ = 5 · 5 · 5 · 5 = 625
2. Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
   −5⁴ = −625

Пример. Вычислить: −6² − (−1)⁴

−6² − (−1)⁴ = −37

1. 6² = 6 · 6 = 36
2. −6² = −36
3. (−1)⁴ = (−1) · (−1) · (−1) · (−1) = 1
4. −(−1)⁴ = −1
5. −36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните!

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Что такое степень числа Свойства степени Возведение в степень дроби

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Значение 4-й степени в астрологии + Примеры

Согласно исследованию покойного сербского астролога Николы Стояновича, значение 4-й степени в астрологии состоит в том, что она несет в себе все домены знака Рака.

Основными доменами знака Рака являются  дом, быть матерью, семейные дела, материнство, забота, забота, плодородие, выращивание чего-либо, эмоции, чувства, безопасное место, гнездо, имущество, земля, страна происхождение, эмоциональная безопасность и многое другое . Здесь вы можете узнать больше о знаке Зодиака Рак.

Связанный пост: Значение степеней в астрологии не Плацид. Однако графики, которые я загрузил, находятся в системе расчета домов Плацидуса. Это может сбивать с толку, заметьте.

Значение степеней, которые я использую как дополнительная информация  для чтения натальной карты.

Итак, давайте посмотрим на несколько реальных примеров значения 4 степени в астрологии.

Обратите внимание, что эти примеры являются очень краткими интерпретациями. Чтобы полностью понять конкретное положение планеты, нужно проверить больше деталей.

Восходящий в 4-й ^-й -й степени — Тони Блэр, бывший премьер-министр Соединенного Королевства

Тони Блэр, бывший премьер-министр Великобритании, имеет Асцендент в 4 ^-м -м градусе Близнецов . Что ж, Близнецы много говорят и произносят речи. Такой благоприятный асекдант для того, чтобы быть политикой и быть политиком. Вся жизнь Тони Блэра связана с его родной страной, а в личной жизни он отец 4 детей от одной матери. Он скорее семейный парень в уединении. Поскольку 4-я степень является аналогией Рака, все о доме, семье, обеспечении безопасного гнезда и т. д.

4-я ^-я -я степень в его случае проявляется не только через его карьеру — работу для своей страны, для своего племени, для своей нации, но и в своей личной жизни.

Астрологическая карта Тони Блэра

Солнце в 4 градусе — Уго Чавес — бывший президент Венесуэлы

Солнце — индикатор карьеры в натальной карте. Здесь вы можете больше узнать о Солнце и о том, почему оно является индикатором карьеры в натальной карте.

Солнце Уго Чавеса находится в 4 ^-м -м градусе Льва. Лев — все о лидерстве, будучи «королем своего собственного королевства». В его случае он был лидером своей нации-Солнца по адресу 4 ^th градус, страна происхождения – аналогия Рака.

Кстати, он был президентом Венесуэлы 14 лет. Что ж, его Солнце находится в аспекте квадрата к Сатурну, что сделало его долговременным — положение лидера. 14 лет — это ровно половина цикла Сатурна.

Hugi Chávez Астрологическая карта

Луна в 4 ^-м -м градусе — Меган, герцогиня Сассекская

Это довольно интересно.

Луна — управитель знака Рак. А Мун показывает эмоции, внутренний диалог натива, главного опекуна, натива как родителя, где натив чувствует себя как дома, чувствует себя комфортно и т. д. 

Асцендентом управителя герцогини Сассекской (Меган Маркл) является Луна, которая расположена в ее 4 ^ом доме в знаке Весов.

Давайте разберемся.

Куда бы ни пошел Асцендентный управитель, у натива есть жгучее желание, иметь это, сделать это, испытать это и т. д. Другими словами, это то, чего натив хочет больше всего в своей жизни.

В ее случае Мун находится в 4 ^м  доме — в доме семьи. Так как он расположен в знаке Весов- семья с супругом, что-то делать с семьей супруга. В ее случае это британская королевская семья.

Однако она не вкладывала слишком много сил и времени в семью своего супруга, как только появилась возможность, она вернулась в свою страну- 4 ^й степени, в свой народ, где она выросла. Вероятно, она чувствовала себя не королевской семьей или Британией, а своей страной. 4-я степень — аналогия с раком, где уроженец чувствует себя как дома.

Меган, герцогиня Сассекская, астрологическая карта

Статья по теме: Секреты 5-го градуса в астрологии, 9-й градус Льва0014

Венера в 4 градусе — Ангела Меркель, бывший канцлер Германии Венера в Деве — в ущербном положении. Это означает, что у нее довольно слабая Дева.

Он расположен в ее 10 доме в знаке Девы в 4 градусе.

Ее Венера управительница ее 11 ^-й  дом – большие сети, цели и мечты. Вероятно, ее целью было стать лидером, так как 11   управитель находится в 10   доме. Лидер в своей стране. Почему? Потому что Венера находится в 4-м градусе, неся аналог Рака, который является домом, нацией и страной происхождения.

астрологическая карта Ангелы Меркель Это не обязательно показатель карьеры, хотя он многое говорит о карьере натива, его мирских достижениях и социальном статусе.

У покойного немецкого диктатора Адольфа Гитлера МС находился в знаке Льва 4-й степени. Поскольку это знак Льва, он хотел стать лидером, большим лидером, как король — аналогия со Львом.

А как насчет 4 ^-й -й степени? Быть лидером своей нации, немцев. Если быть точным, он был австрийцем, но его намерением было сделать Германию и Австрию 3 ^rd империей и править миром.

Его идея заключалась в том, чтобы сделать свою нацию — сверхчеловека над всеми нациями, правящей нацией. Остальное уже история. 4-я степень – аналогия с Раком, что означает «мое племя», «мой народ» и «моя страна».

Есть ли у вас планеты или углы в 4-м градусе? Как это проявляется в вашей жизни? Приветствуется каждый личный опыт; мы все можем многому у них научиться.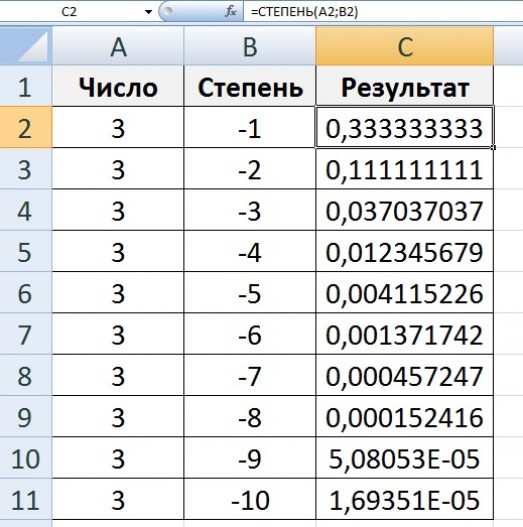 Привет, Ники

• Поделиться в Твиттере Поделиться в Твиттере
• Поделиться на Facebook Поделиться на Facebook
• Поделиться на Pinterest Поделиться на Pinterest
• Поделиться в LinkedIn Поделиться в LinkedIn
• Поделиться на Reddit Поделиться на Reddit
• Поделиться по электронной почте Поделиться по электронной почте

Связанные статьи, серия степеней:

Тайны степеней

0 степень

Овен степеней: 1 9 0038-й -й градус, и 13 ^-й -й градус, и 25 ^-й -й градус

градусы Тельца: 2 ^и градусы, и 14 ^й градусы, и 26 ^й градусы

градусы Близнецов: 3 ^-й -й градус и 15 ^-й -й градус и 27 ^-й -й градус

Раковый градус: 4-й ^-й -й градус и 16 ^{-й 90-й градус 039 градус и 28 -й градус}

градус Льва: 5 ^-й -й градус и 17 ^-й -й градус и 29 ^-й -й градус

градус Девы: 6-й ^-й -й градус и 18-й ^-й градус

градус Весов: 7 ^й градус и 19^-й -й градус

градусы Скорпиона: 8 ^-й -й градус и 20 ^-й -й градус

градусы Стрельца: 9 90 038-й -й градус и 21-й ^-й -й градус

градус Козерога: 10 ^-й градус и 22 ^й градус

градусы Водолея: 11 ^й градус и 23 ^й градус

9 0013 градусов Рыб: 12 ^й градус и 24 ^th  степень

Вам также могут понравиться:

Доверяйте времени своей жизни

Вы будете жить в другой стране?

Станешь ли ты богатым? Показатели богатства в натальной карте

Эпоха Водолея

Что означает критический градус в карте рождения

Духовность

|Экспертная оценка

Автор:

Сара Риган

Эксперт-рецензент:

The AstroTwins

16 ноября 2021 г.

mbg Редактор журнала «Духовность и отношения»

Сара Риган

mbg Редактор журнала «Духовность и отношения» 900 07

Сара Риган — редактор журнала «Духовность и отношения» и зарегистрированный инструктор по йоге. . Она получила степень бакалавра в области радиовещания и массовых коммуникаций в Университете штата Нью-Йорк в Освего и живет в Буффало, штат Нью-Йорк.

Экспертная оценка

The AstroTwins

Астрологи

Офира и Тали Эдут, известные как AstroTwins, являются профессиональными астрологами из Нью-Йорка и Сиэтла. Их работы были представлены в The New York Times, Elle Magazine, Vogue и Good Morning America, и они являются авторами AstroStyle, Love Zodiac, Shoesstrology и Momstrology.

16 ноября 2021 г.

Чем глубже вы погружаетесь в свою карту рождения, тем больше понимаете, что астрология — это гораздо больше, чем ваш солнечный знак и ежедневный гороскоп. Одним из многих факторов, влияющих на карту рождения, являются градусы определенных планет, причем каждый знак имеет определенный «критический градус» во время вашего рождения. Вот каковы критические степени, а также что они говорят о вашей личности и жизненных проблемах, согласно AstroTwins.

Реклама

Это объявление отображается с использованием стороннего контента, и мы не контролируем его функции доступности.

Каковы критические степени?

Как близнецы объясняют mbg: «В астрологии есть «критические градусы» в зодиакальном колесе, которые, как считается, создают дополнительную проблему, когда планета прибывает сюда или находится здесь в момент вашего рождения». Эти критические степени зависят от того, смотрите ли вы на кардинальный, фиксированный или изменчивый знак. (Вы можете рассчитать свою карту рождения здесь, чтобы узнать градусы в вашей карте!)

Краткий обзор критических градусов для знаков:

• Кардинальные знаки (Овен, Рак, Весы и Козерог): 0, 13 и 26 градусы
• Фиксированные знаки (Телец, Лев, Скорпион и Водолей): 8-9 и 21-22 градусы
• Мутабельные знаки (Близнецы, Дева, Стрелец и Рыбы): 4 и 17 градусы

Реклама

Это объявление отображается с использованием стороннего контента и мы не контролируем его функции доступности.

Венера в Тельце в 9 градусе будет считаться критическим градусом, например, или Меркурий в Козероге в 26 градусе.

Что это значит, если в вашей карте есть критические степени?

Критические градусы, как правило, сигнализируют о проблемах в зодиакальной карте. Как объясняют близнецы, критические градусы «могут усилить влияние планеты в вашей карте, потому что в этой сфере жизни вам придется немного поработать». Они добавляют, что в некотором смысле наличие критических степеней в вашей карте сравнимо с рождением с ретроградной планетой.

«Хотя у вас могут быть дополнительные трудности, — отмечают они, — прорыв сделает вас неудержимым и самодостаточным, чего другие люди никогда не смогут достичь».

И, конечно же, поскольку в астрологии нет ничего черного и белого, близнецы добавляют, что важно помнить, что любой градус может иметь значение в карте, если планета образует аспект (особый угол, равный 0°, 60° , 90°, 120° или 180°) к другой планете на карте.