deg | CSS | WebReference
- Содержание
- Пример
- Спецификация
- Браузеры
Единица deg определяет угол в градусах. Прямой угол равен 90 градусов, полный оборот соответствует 360 градусам. Допустимо использовать отрицательное значение (-90deg), нулевое (0deg) и дробное (36.6deg).
Значения некоторых углов представлены в табл. 1.
| 0deg | |
| 90deg | |
| 180deg | |
| 270deg | |
| -90deg |
Пример
<!DOCTYPE html> <html> <head> <meta charset=»utf-8″> <title>deg</title> <style> body { background: linear-gradient(45deg, #017bed, #fff) fixed; } </style> </head> <body> <p>Пример текста</p> </body> </html>В данном примере для веб-страницы выводится градиент, наклоненный под углом 45 градусов.
Спецификация
| Спецификация | Статус |
|---|---|
| CSS Values and Units Module Level 4 | Рабочий проект |
| CSS Values and Units Module Level 3 | Возможная рекомендация |
Спецификация
Каждая спецификация проходит несколько стадий одобрения.
- Recommendation (Рекомендация) — спецификация одобрена W3C и рекомендована как стандарт.
- Candidate Recommendation (Возможная рекомендация) — группа, отвечающая за стандарт, удовлетворена, как он соответствует своим целям, но требуется помощь сообщества разработчиков по реализации стандарта.
- Proposed Recommendation (Предлагаемая рекомендация) — на этом этапе документ представлен на рассмотрение Консультативного совета W3C для окончательного утверждения.
- Working Draft (Рабочий проект) — более зрелая версия черновика после обсуждения и внесения поправок для рассмотрения сообществом.
- Editor’s draft (Редакторский черновик) — черновая версия стандарта после внесения правок редакторами проекта.
- Draft (Черновик спецификации) — первая черновая версия стандарта.
Браузеры
| 9 | 12 | 2 | 12 | 4 | 3.6 |
| 4 | 4 | 12 | 4 |
Браузеры
В таблице браузеров применяются следующие обозначения.
- — свойство полностью поддерживается браузером со всеми допустимыми значениями;
- — свойство браузером не воспринимается и игнорируется;
- — при работе возможно появление различных ошибок, либо свойство поддерживается лишь частично, например, не все допустимые значения действуют или свойство применяется не ко всем элементам, которые указаны в спецификации.
Число указывает версию браузера, начиная с которой свойство поддерживается.
Автор и редакторы
Автор: Влад Мержевич
Последнее изменение: 28.09.2019
Редакторы: Влад Мержевич
deg — Викисловарь
Текущая версия (не проверялась)
- 1 Английский
- 1.1 Морфологические и синтаксические свойства
- 1.2 Произношение
- 1.3 Семантические свойства
- 1.3.1 Значение
- 1.3.2 Синонимы
- 1.3.3 Антонимы
- 1.3.4 Гиперонимы
- 1.3.5 Гипонимы
- 1.4 Родственные слова
- 1.5 Этимология
- 1.6 Фразеологизмы и устойчивые сочетания
- 2 Валлийский
- 2.1 Морфологические и синтаксические свойства
- 2.2 Произношение
- 2.3 Семантические свойства
- 2.3.1 Значение
- 2.3.2 Синонимы
- 2.3.3 Антонимы
- 2.3.4 Гиперонимы
- 2.3.5 Гипонимы
- 2.4 Родственные слова
- 2.5 Этимология
- 2. 6 Фразеологизмы и устойчивые сочетания
- 3 Волапюк
- 3.1 Морфологические и синтаксические свойства
- 3.2 Произношение
- 3.3 Семантические свойства
- 3.3.1 Значение
- 3.3.2 Синонимы
- 3.3.3 Антонимы
- 3.3.4 Гиперонимы
- 3.3.5 Гипонимы
- 3.4 Родственные слова
- 3.5 Этимология
- 3.6 Фразеологизмы и устойчивые сочетания
- 4 Корнский
- 4.1 Морфологические и синтаксические свойства
- 4.2 Произношение
- 4.3 Семантические свойства
- 4.3.1 Значение
- 4.3.2 Синонимы
- 4.3.3 Антонимы
- 4.3.4 Гиперонимы
- 4.3.5 Гипонимы
- 4.4 Родственные слова
- 4.5 Этимология
- 4.6 Фразеологизмы и устойчивые сочетания
- 5 Норвежский
- 6 Шведский
- 6.1 Морфологические и синтаксические свойства
- 6.2 Произношение
- 6.3 Семантические свойства
- 6.3.1 Значение
- 6. 3.2 Синонимы
- 6.3.3 Антонимы
- 6.3.4 Гиперонимы
- 6.3.5 Гипонимы
- 6.4 Родственные слова
- 6.5 Этимология
- 6.6 Фразеологизмы и устойчивые сочетания
- 6.7 Библиография
6 Фразеологизмы и устойчивые сочетания
3.2 СинонимыМорфологические и синтаксические свойства
deg
Существительное.
Корень: —.
Произношение
Семантические свойства
Значение
- степень ◆ Отсутствует пример употребления (см. рекомендации).
- градус ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- degree
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
| |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
deg
Числительное.
Корень: —.
Произношение
Семантические свойства
Значение
- десять ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Для улучшения этой статьи желательно:
|
deg
Местоимение.
Объектный падеж личного местоимения du.
| В шведск. Википедии есть статья «deg». |
Морфологические и синтаксические свойства
| падеж | ед. ч. | мн. ч. | ||
|---|---|---|---|---|
| неопр. | опр. | неопр. | опр. | |
| Им. | deg | degen | degar | degarna |
| Р. | degs | degens | degars | degarnas |
deg
Существительное, общий род.
Корень: —.
Произношение
Семантические свойства
Значение
- кулин. тесто ◆ Отсутствует пример употребления (см. рекомендации).
- жарг. бабло, деньги ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
Антонимы
Гиперонимы
- livsmedel
Гипонимы
Родственные слова
| Ближайшее родство | |
| |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Библиография
- deg, Svenska Akademiens ordlista över svenska språket (14-e изд. 2015)
- deg, Svenska Akademiens ordbok
- deg, Svensk-rysk ordbok (1959)
2015) Для улучшения этой статьи желательно:
|
Измерение углов
Измерение угловКонцепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов. Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Градусы могут быть разделены на минуты и секунды, но это деление уже не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых 9.0004 секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часов на минуты и секунды времени. |
Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы рассмотрим углы больше 360° и отрицательные углы.Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°.
Когда для анализа нарисован один угол на плоскости xy , мы нарисуем его за стандартная позиция с вершиной в начале координат (0,0), одна сторона угла вдоль оси x , а другая сторона над осью x .
радианы
Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно, а также Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом.
Например, Леонард Эйлер (1707–1783) в своих « элементах алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности.
Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах.
Так как площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . Его, конечно, можно было бы представить десятичным числом, но радианное измерение часто появляется с коэффициентом 9.0004 № .| Уголок | градусов | радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г.
Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минуты, радиус от центральной линии пути составляет 2100 футов.
Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известно, что воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Итак, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы.
Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23.
Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть
2102.5 a – 1997.5 a , что равно 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.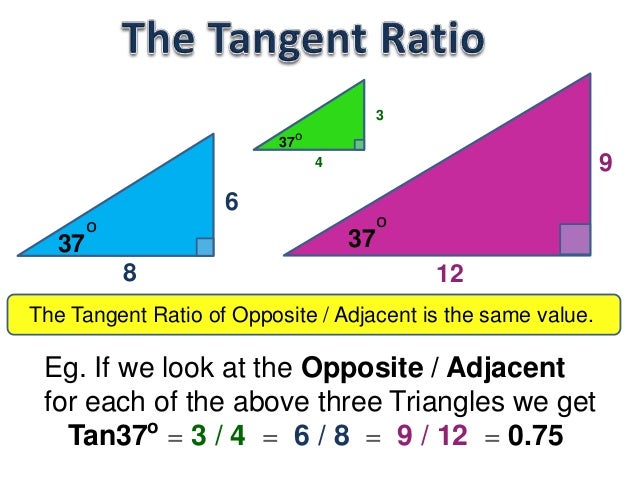
Другой пример см. в задаче 3(а). Данные равны 0°17’48» и 6,2935 с точностью до 4 и 5 цифр соответственно. Поэтому ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не считая ведущих нулей) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранить все цифры для промежуточных вычислений.
Преобразование температуры
Во всем мире существует множество различных единиц измерения температуры. Три самых важных из них — Фаренгейты (F), Кельвины (K) и Цельсия (C).
Основные факты и выводы- Шкалы Цельсия и Фаренгейта являются градусными шкалами. Символ градуса не используется для обозначения температуры по шкале Кельвина, вместо этого они отмечаются как кельвины.
- Вода кипит при 100 градусах Цельсия или 212 градусов по Фаренгейту, или 373,15 Кельвина.
- Вода замерзает при 0 градусов по Цельсию или 32 градуса по Фаренгейту, или 273,15 по Кельвину.
- Абсолютный ноль равен 0 градусов Кельвина. Это самая низкая температура, до которой может опускаться любое вещество.
- Цельсия и Фаренгейта одинаковы при -40 градусах, так как шкалы сходятся.
- При высоких температурах градусы Цельсия и Кельвина становятся равными, поскольку разница в 273,15 между ними теряется в шуме.
- 0 градусов Цельсия равно 32 градусам по Фаренгейту. Основная формула: ( °C × 9/5) + 32 = °F.
- 0 градусов Цельсия равно 273,15 Кельвина. Основная формула: °C + 273,15 = K.
- Основная формула для преобразования градусов Фаренгейта в градусы Цельсия: ( °F — 32) × 5/9 = °C.
- Чтобы преобразовать градусы Фаренгейта в кельвины, ( °F — 32) × 5/9 + 273,15 = К.
- 0421 °C, , а формула преобразования Кельвинов в градусы Фаренгейта: ( K – 273,15) × 9/5 + 32 = °F.
- Температуру можно просто определить как меру тепла или холода объекта.
- Температура измеряется с помощью термометра – мы наблюдаем влияние температуры на вещество внутри него.
Используем ли мы градусы Цельсия, Фаренгейта или Кельвина при измерении температуры, не так важно. Однако, если мы окажемся в определенных регионах, где измерение температуры отличается, знание различий между тремя наиболее часто используемыми системами может пригодиться.
Все три являются правильными способами измерения температуры, и все они могут быть получены друг из друга с помощью формул, поскольку они связаны друг с другом.
Но отличаются ли эти единицы измерения чем-либо друг от друга, кроме их различных значений? Да и нет, и здесь немного о каждом из них.
Шкала, также называемая стоградусной, основана на 0 градусах для точки замерзания воды и 100 градусах для точки кипения воды. Эта система была изобретена в 1742 году шведским астрономом Андерсом Цельсиусом.
Некоторые до сих пор называют ее стоградусной шкалой из-за 100-градусного интервала между заданными точками. Шкала Цельсия является частью метрической системы и используется для измерения температуры во многих странах.
Это самые простые в использовании весы, и хотя они используются во всем мире, есть одно исключение — США. В США преобладает шкала Фаренгейта, но шкала Цельсия также не принимается в некоторых местах, где используется шкала Кельвина.
Нормальная температура человеческого тела 32 °C, а значение абсолютного нуля установлено на -273,15 °C по этой шкале. Преобразовать градусы Цельсия в градусы Фаренгейта довольно просто:
°C в °F : умножьте на 9, затем разделите на 5 и прибавьте 32.
.
Первый шаг: 28°C × 9/5 = 252/5 = 50,4.
Второй шаг: 50,4 + 32 = 82°F.
Шкала Цельсия и шкала Фаренгейта совпадают при -40° , что одинаково для обоих. Когда дело доходит до преобразования градусов Цельсия в кельвины, формула еще проще.
0 градусов Цельсия равно 273,15 Кельвина. Основная формула: °C + 273,15 = K. Кельвинов в градусах Цельсия : Добавьте 273.
Пример: как преобразовать 28°C в градусы Кельвина (K).
Первый шаг: 28°C + 273,15 = 301,15 K
ФаренгейтыЭта температурная шкала основана на 32 градусах для точки замерзания воды и 212 градусах для точки кипения. Интервал между двумя точками делится на 180 равных частей.
Немецкий физик Даниэль Габриэль Фаренгейт изобрел эту шкалу в 1724 году. Средняя температура человеческого тела составляет 98,6°F, а абсолютный ноль по этой шкале равен -459,67°F.
Шкала Фаренгейта принята и используется в Соединенных Штатах и на некоторых их территориях. Чтобы преобразовать градусы Фаренгейта в градусы Цельсия, вот формула:
°F в °C : вычтите 32, затем умножьте на 5, затем разделите на 9. Основная формула: (°F – 32) × 5/9 = °C или точно (F – 32)/1,8.
Пример : Как перевести 98,6° по Фаренгейту в градусы Цельсия (°C)
Первый шаг: 98,6°F – 32 = 66,6.
Второй этап: 66,6 × 5/9 = 333/9 = 37°C.
Когда дело доходит до перевода градусов Фаренгейта в кельвины, формула еще проще.
Вычтите 32, умножьте на 5, разделите на 9, затем прибавьте 273,15. Пример 0011 (98,6 °F − 32) × 5/9 + 273,15 = 310,15 К
Кельвин Эта температурная шкала названа в честь британского математика и физика Уильяма Томсона Кельвина, который предложил ее в работе1. абсолютная температурная шкала, имеющая абсолютный нуль, ниже которого температура не существует.
Каждая единица этой шкалы называется кельвином, а не градусом. По этой причине при указании температуры в градусах Кельвина используется только буква K, а не символ градуса ° . На шкале Кельвина нет отрицательных чисел, так как наименьшее число равно 0 К.
Абсолютный нуль технически недостижим. Это температура, при которой молекулы перестают двигаться — таким образом, она «бесконечно холодная».
Температура замерзания воды в градусах Кельвина составляет 273,15К, а температура кипения 373,15К. Идея шкалы Кельвина возникла после открытия в 1800-х годах связи между объемом и температурой газа.
Что касается других шкал, Кельвины и Цельсии становятся равными при высоких температурах, так как разница между ними в 273,15 теряется в шуме.
Чтобы перевести кельвины в градусы Цельсия, достаточно использовать простую формулу.
K до ° C : добавить 273
K — 273,15 = ° C
Пример: Как преобразовать 35 ° C в Kelvin (K)
111111111111111111111111111111111111111111111111111111111111 35 1111111111111111111111111111111111111111111111.
35 11111111111111111111111111. 308,15 К
Чтобы перевести кельвины в градусы Фаренгейта, используйте формулу:
( К — 273,15) × 9/5 + 32 = °F.
Вычтите 273,15, умножьте на 1,8, затем прибавьте 32,
Example: How to convert 75°F into Kelvin (K)
(75 °F − 32) × 5/9 + 273.15 = 297.039 K
Fun Facts- The hottest зарегистрированная на Земле температура 57,8°C / 136°F, зарегистрированная в Аль-Азизии, Ливия, 13 сентября 1922 г.
- Антарктида, 21 июля 1983 года.
- В США одна из самых высоких температур, когда-либо зарегистрированных, составляла 56,7 ° C / 134 ° F, зарегистрированная в Долине Смерти, Калифорния, 10, 19 июля.13.
- В Новой Зеландии самая высокая зарегистрированная температура составляет 42,4°C / 108,3°F, зарегистрированная в Рангиоре и Мальборо 7 февраля 1973 года.
- В Африке самая низкая зарегистрированная температура составляет -24°C / — 11°F, зафиксировано в Ифране, Марокко, 11 февраля 1935 года.
- Изобретатель шкалы Кельвина также написал второй закон термодинамики, который гласит, что тепло не переходит от более холодного тела к более горячему.
- Kelvin to Fahrenheit: Subtract 273.15, multiply by 1.8, then add 32
- Fahrenheit to Kelvin: Subtract 32, multiply by 5, divide by 9, then add 273.15
- Kelvin to Celsius : Add 273
- Celsius to Kelvin: Subtract 273
- Fahrenheit to Celsius: Subtract 32, multiply by 5, then divide by 9
- Celsius to Fahrenheit: Умножьте на 9, разделите на 5, а затем прибавьте 32
Не так давно в стекле термометров была ртуть.
Если температура повышалась, ртуть расширялась и поднималась вверх по узкой трубке.
Мы могли видеть температуру, считав ее по шкале цифр на трубке. Однако ртуть очень токсична, и вскоре ее заменили различными жидкостями.
Концепция остается неизменной независимо от того, что при повышении температуры жидкость расширяется и поднимается вверх, а при понижении температуры жидкость сжимается и стекает по трубке.
Знаете ли вы?- Шкала Кельвина — не единственная шкала абсолютной температуры. Существует также температурная шкала Ренкина. Используется в основном инженерами.
- Неизвестно, был ли Даниэль Габриэль Фаренгейт масоном, однако многие считают, что он им был, потому что существует 32 степени просветления , и он решил использовать 32 в качестве температуры плавления воды на своей шкале.
- Андерс Цельсий изобрел шкалу температуры в 1742 году с помощью ртутного термометра.
- Unit Converter Bot
- Biodifferences
- Unit Converter
- LiveScience
- Britannica
- Wikipedia
- https://static.
