Все формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
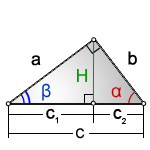 H — высота из прямого угла
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
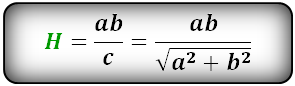
Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):
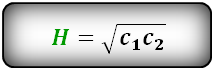
- Подробности
- Автор: Administrator

Высота треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Высота, проведенная в любом треугольнике, делит его на два прямоугольных треугольника, становясь смежным катетом. Сторона, на которую опущена высота, оказывается также разделенной на две пропорциональных части. Зная все три стороны, можно собрать их по теореме Пифагора, и приравняв высоту в качестве катета в двух вышеуказанных треугольниках, получить ее формулу для любого произвольного треугольника: 
С другой стороны, можно использовать сторону, прилежащую к высоте и угол α, чтобы вычислить высоту треугольника.

Известная его сторона будет гипотенузой в прямоугольном треугольнике, а сама высота – катетом, противолежащим углу α. Два этих измерения связывает синус угла, поэтому высота равна его произведению на сторону a: h=a sinα
Высота в прямоугольном треугольнике, опущенная из прямого угла (остальные две совпадают с катетами), получает особые свойства. Так как все три получившихся прямоугольных треугольника подобны друг другу, их стороны составляют пропорцию, которая раскладывается как квадрат высоты, равный произведению проекцию катетов на гипотенузу, или проще говоря, частей гипотенузы, на которые ее делит высота.

Из этого следует, что высота равна квадратному корню из данного произведения, а это есть не что иное как среднее пропорциональное приведенного выражения.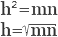
В равностороннем треугольнике, высота делит угол, из которого она исходит, на два одинаковых угла по 30°. Высота, оказываясь катетом, прилежащим к этому углу, внутри прямоугольного треугольника, подчиняется отношению косинуса угла α, а так как  , а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так:
, а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так: 
Все формулы для треугольника
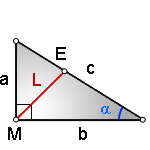
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
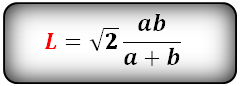
Формула длины биссектрисы через гипотенузу и угол, ( L):
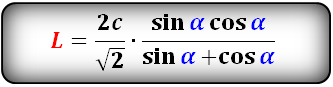
2. Найти по формулам длину биссектрисы из острого угла на катет:
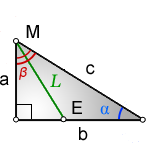
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
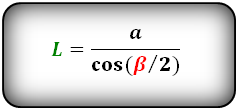
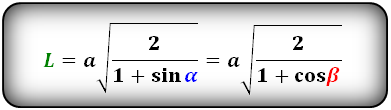
Формула длины биссектрисы через катет и гипотенузу, (L):
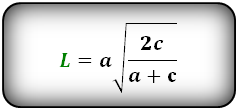
Высота треугольника | Онлайн калькулятор
В произвольном треугольнике (у которого все стороны разной длины), высоты, проведенные к сторонам , медианы и биссектрисы представляют собой совершенно разные линии. Чтобы найти длину высоты в треугольнике, нельзя будет использовать свойства медианы или биссектрисы, как для равнобедренных или равносторонних треугольников, поэтому придется использовать другие методы.
Один из подобных методов заключается в использовании общего параметра треугольника — площади. Алгоритм вычислений строится на том, что площадь разностороннего треугольника можно найти несколькими способами, в том числе и через высоту. Зная три стороны треугольника, можно найти его площадь по формуле Герона, а затем используя другую формулу площади, выразить через нее высоту.
Чтобы вычислить площадь треугольника по формуле Герона, нужно сначала рассчитать полупериметр треугольника. Как следует из названия, полупериметр — это периметр, то есть сумма длин всех трех сторон, деленный на два.
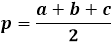
Сама формула площади представляет собой произведение полупериметра на его разности с каждой стороной, все это выражение будучи заключенным под квадратным корнем. 
С другой стороны та же площадь треугольника через высоту равна половине произведения стороны треугольника на высоту, на нее опущенную. Отсюда высота будет равна отношению удвоенной площади к стороне треугольника. Из предыдущей формулы можно выразить площадь через три стороны треугольника и заменить ее в формуле высоты.
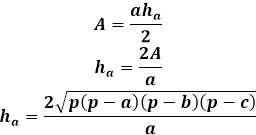
Данная формула высоты через стороны треугольника применима для любых треугольников, произвольных, равнобедренных или равносторонних за отсутствием других.
Вычисляя высоту треугольника, зная три стороны, приходится идти длинным путем, используя формулы площади. Высота треугольника, выраженная через площадь, связана только с той стороной, на которую она опущена, поэтому чрезвычайно важно правильно указать для калькулятора порядок сторон и в ручном расчете подставить соответствующую сторону в формулу высоты.
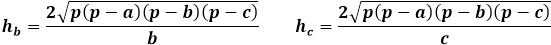
Формула высоты произвольного треугольника через площадь 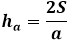
Высота равнобедренного треугольника | Онлайн калькулятор
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
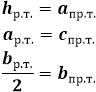
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
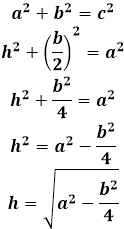
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:

Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
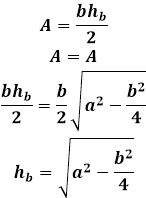
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β: 
Формула через основание и угол при нем α: 
через основание и угол противолежащий ему β: 
Уравнение высоты треугольника | Треугольники
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Все формулы высоты трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
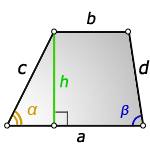
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):
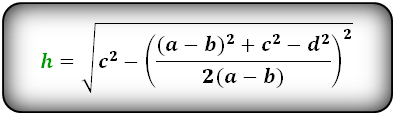
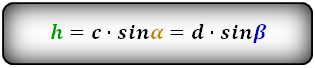
2. Формула высоты трапеции через диагонали и углы между ними
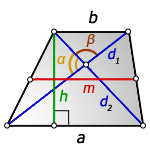
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
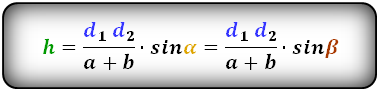
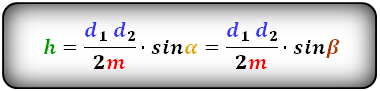
3. Формула высоты трапеции через площадь
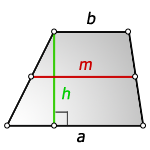
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
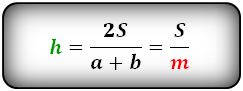
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии

