Квадрат, треугольник, круг. Для вас, мальчишки
Квадрат, треугольник, круг
Предлагаем нарисовать из геометрических фигур человечка. Используем круги, прямоугольники и треугольники. В твоем рисунке могут присутствовать равносторонние треугольники, треугольники с прямым углом, вертикальные прямоугольники, горизонтальные прямоугольники, очень вытянутые прямоугольники, квадраты, овалы и т. д., но не должно быть звезд, пятиугольников, трапеций и прочих геометрических фигур, которые не относятся ни к одной из требуемых групп. Ты можешь использовать фигуры разных размеров, накладывать одну фигуру на другую. Главное – придерживаться следующих требований:
1. Общее количество фигур в одном человечке должно быть равно 10, ни больше и ни меньше.
2. В изображении человечка должны быть использованы все три вида геометрических фигур.
Если к концу рисования ты обнаружишь, что человечек содержит более 10 элементов, то лишние фигуры необходимо удалить.
Следуя правилам, из геометрических фигур необходимо нарисовать 3 человечка.
После выполнения задания подсчитай количество кругов, прямоугольников и треугольников отдельно во втором и в третьем человечке. Полученные результаты запиши в виде двух трехзначных чисел. Трехзначное число – это «формула рисунка», в которой первая цифра означает количество треугольников, вторая цифра – количество кругов и третья цифра – количество прямоугольников. Например, 325 – это 3 треугольника, 2 круга и 5 прямоугольников.
А теперь самое интересное. Дело в том, что соотношение геометрических элементов в нарисованных тобой человеческих фигурках неслучайно. Изображая человечка из треугольников, кругов и квадратов, ты как бы рисуешь свой автопортрет. Какой именно – смотри ниже.
Все возможные формулы рисунка можно объединить в 8 типов.
Лидер: этому типу соответствуют формулы 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640.
Если твои рисунки относятся к данному типу, то у тебя, определенно, есть склонности к организаторской деятельности и лидерские способности. Ты любишь руководить, и у тебя это неплохо получается. Ты легко приспосабливаешься к любой ситуации. Особенно сильно черты лидера выражены у подтипов 901, 910, 802, 811 и 820. Подтипы 703, 712, 421 и 730 проявляют лидерские качества время от времени. А 604, 613, 622, 631 и 640 являются хорошими рассказчиками и обладают редким даром убеждения, благодаря которому могут воздействовать на других людей.
Труженик: 505, 514, 523, 532, 541, 550. Труженик очень похож на Лидера, но в отличие от него в ответственные минуты, когда требуется принять важное решение, начинает колебаться, взвешивать все «за» и «против». У тебя сильно развито чувство ответственности и стремление к совершенству. Что бы ты не делал, ты все пытаешься выполнить на «отлично». Высокая требовательность себе соседствует с неменьшей требовательностью к окружающим тебя людям.
Артист: 406, 415, 424, 433, 442, 451, 460. У тебя много талантов и, как следствие, много увлечений. Ты физически не переносишь грязь и беспорядок, что может стать причиной для конфликта с людьми, менее щепетильными в данном вопросе. Ты очень раним, часто сомневаешься в себе, но если тебя хвалят, то расцветаешь буквально на глазах. Подтип 415 часто обладает поэтической одаренностью, а 424 отличается особой тщательностью в работе.
Ученый: 307, 316, 325, 334, 343, 352, 361, 370. У тебя буквально на все есть своя теория. Любой свой поступок, прежде чем совершить, ты тщательно продумываешь. И вообще, отличаешься «концептуальным» умом и редким душевным равновесием.
Психолог: 208, 217, 226, 235, 244, 253, 262, 271, 280.
Тебя отличает высокая чувствительность и заботливость в отношении других людей. В ситуациях несправедливости ты часто встаешь на сторону обиженных. При этом отрицательно реагируешь на любые попытки посягнуть на твою личную свободу. Любишь все новое, часто обладаешь богатым воображением и ручными умениями в прикладных видах искусства. Если ты – подтип 235, то не пора ли тебе заняться психологией? Подтип 244 нередко обладает литературными способностями, а 217 – способностями к изобретательской деятельности.
Любишь все новое, часто обладаешь богатым воображением и ручными умениями в прикладных видах искусства. Если ты – подтип 235, то не пора ли тебе заняться психологией? Подтип 244 нередко обладает литературными способностями, а 217 – способностями к изобретательской деятельности.
Изобретатель: 109, 118, 127, 136, 145, 019, 028, 037, 046.
Природа наградила тебя богатым воображением и «технической жилкой», позволяющей заниматься самыми разными видами технического творчества. Особенно сильно выраженными возможностями к изобретательской деятельности отличается подтип 118. Ты не любишь, когда тебя норовят подвести под общую гребенку, и всегда поступаешь так, как сам считаешь нужным. Свой богатый внутренний мир предпочитаешь шумным вечеринкам и праздному веселью. Часто бываешь одержим собственными оригинальными идеями.
Чувствительный: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.
Ты тяжело переживаешь жестокие сцены в кино и близко к сердцу принимаешь несчастья и проблемы окружающих тебя людей.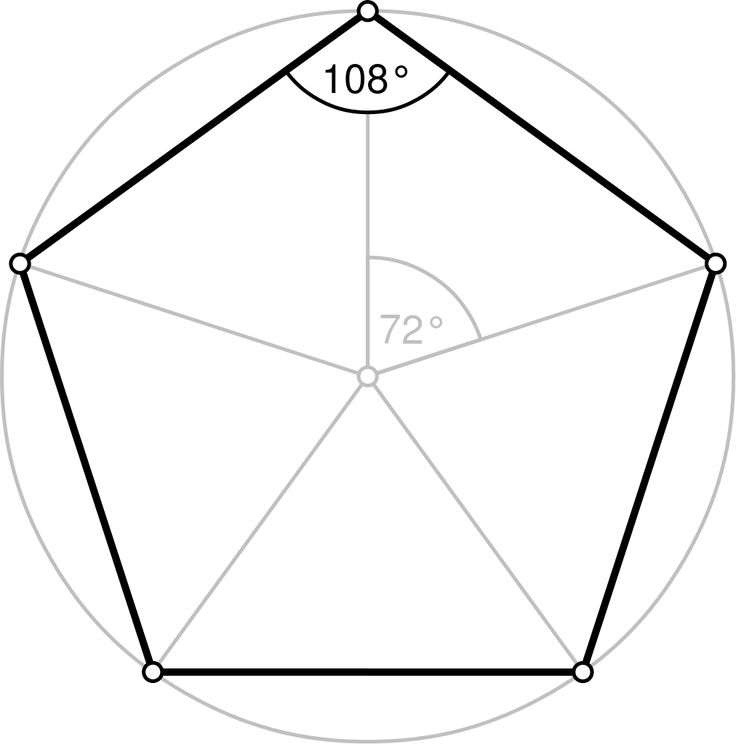 Неприятные события, произошли ли они в жизни или были увидены тобой по телевизору, ты переживаешь долго и глубоко. На сопереживание и сочувствие другим людям у тебя уходит слишком много энергии, в результате становится затруднительной реализация твоих собственных способностей.
Неприятные события, произошли ли они в жизни или были увидены тобой по телевизору, ты переживаешь долго и глубоко. На сопереживание и сочувствие другим людям у тебя уходит слишком много энергии, в результате становится затруднительной реализация твоих собственных способностей.
Эгоист: 901, 802, 703, 604, 505, 406, 307, 208, 109.
Если ты относишься к данному типу, то чужие переживания и эмоции для тебя словно не существуют. Ты невнимателен и время от времени черств. Особенно сильно твоя эгоистичность проявляется в тех случаях, когда тебя одолевают собственные проблемы. Ты склонен заставлять других людей делать то, что хочется именно тебе, не считаясь с их потребностями.
Данный текст является ознакомительным фрагментом.
Упражнение 28. Треугольник
Упражнение 28.
Упражнение 47. Треугольник (вариант)
Упражнение 47. Треугольник (вариант) Этот метод нужно объединить с тем, который был дан выше (стр. 86-87). Повернувшись направо, затем налево и наклонив туловище, возвратитесь в исходное положение: встаньте прямо, ноги врозь, руки вытянуты горизонтально по линии плеч. Не
Треугольник любви
Треугольник любви
Мы можем представить любовь в виде треугольника, каждый угол которого соответствует одному из неотделимых ее свойств. Не может быть треугольник без трех углов и не может быть истинной любви без трех следующих свойств.
Глава 9. Третий треугольник.
Глава 9. Третий треугольник. В этой главе мы поговорим об активации третьего силового треугольника чакр при третьем посвящении, и о некоторых следствиях из этого процесса. В предыдущих книгах мы довольно подробно описали ряд механизмов, связанных с инициацией центров в
Квадрат, треугольник, круг
Квадрат, треугольник, круг Предлагаем нарисовать из геометрических фигур человечка. Используем круги, прямоугольники и треугольники. В твоем рисунке могут присутствовать равносторонние треугольники, треугольники с прямым углом, вертикальные прямоугольники,
Рисование закрашенных кругов и треугольников на Raspberry Pi Pico с помощью MicroPython / Хабр
Библиотека framebuf — это то, что, при разработке на MicroPython, даёт нам возможности по работе с основными графическими элементами. Например — с текстовыми символами, с прямоугольниками, да и с отдельными пикселями. Это позволяет создать множество интересных изображений. Но весьма полезно оснастить MicroPython ещё и возможность рисования закрашенных треугольников, кругов и колец.
Например — с текстовыми символами, с прямоугольниками, да и с отдельными пикселями. Это позволяет создать множество интересных изображений. Но весьма полезно оснастить MicroPython ещё и возможность рисования закрашенных треугольников, кругов и колец.
Закрашенные круги
В этом руководстве речь пойдёт о реализации этих полезных мелочей. Здесь же будут продемонстрированы возможности недорогого цветного дислея, состыкованного с Raspberry Pi Pico.
Материалы
Для того чтобы воспроизвести то, о чём я расскажу, вам понадобятся следующие комплектующие и программы:
- Программируемый микроконтроллер Raspberry Pi Pico.
- Цветной LCD-дисплей Waveshare разрешением 160×80 пикселей с диагональю 0,96 дюйма, выполненный в форм-факторе модуля для Raspberry Pi Pico.
- USB-кабель.
- Редактор Thonny.
Шаг 1. Дисплей
Изображение, выведенное на дисплее
У выбранного мной дисплея имеются разъёмы, соответствующие пинам Pi Pico. Для соединения двух устройств достаточно лёгкого нажатия. Правда, не стоит нажимать на экран, давление надо прикладывать только к плате дисплея. Нужно, кроме того, правильно его ориентировать — так, чтобы джойстик находился бы с той стороны, где у Pi Pico расположен USB-разъём. Джойстик и кнопки, которыми оснащён дисплей, будут использованы в наших проектах в роли простых устройств ввода информации.
Для соединения двух устройств достаточно лёгкого нажатия. Правда, не стоит нажимать на экран, давление надо прикладывать только к плате дисплея. Нужно, кроме того, правильно его ориентировать — так, чтобы джойстик находился бы с той стороны, где у Pi Pico расположен USB-разъём. Джойстик и кнопки, которыми оснащён дисплей, будут использованы в наших проектах в роли простых устройств ввода информации.
Обычно, когда рекламируют подобные дисплеи, на них выводят цветные фотографии. Наш дисплей вполне на такое способен. Снимок экрана, приведённый в начале раздела, это подтверждает. Ниже я расскажу о том, как это делается. Правда, большая часть этого материала посвящена не тому, как выводить на дисплей готовые изображения, а тому, как создавать и выводить что-то своё.
Шаг 2. Изучение документации
Справка по плате дисплея
Дисплей
Документацию по дисплею можно найти здесь. На неё стоит взглянуть.
Компания Waveshare предлагает пользователям пример программы с включённым в её состав драйвером дисплея, а не отдельную библиотеку для работы с дисплеем. (Мне нравится такой подход, так как он избавляет от необходимости постоянной возни с библиотеками при смене периферийных устройств).
Вот — моя, немного дополненная, версия этого примера. Она выводит линии и текст, поддерживает работу джойстика и кнопок. Драйвер — это самая важная часть программы. Его код нужно включать в состав всех программ, которые работают с дисплеем.
Шаг 3. Рисование кругов
Теорема Пифагора
Если нарисовать в круге радиус, а так же — вертикальные и горизонтальные линии, формирующие прямоугольные треугольники, можно воспользоваться теоремой Пифагора для того чтобы найди длину стороны a для любого значения i. Если нарисовать горизонтальные линии длины a в обоих направления от вертикального диаметра — они коснутся обеих сторон круга по его границе.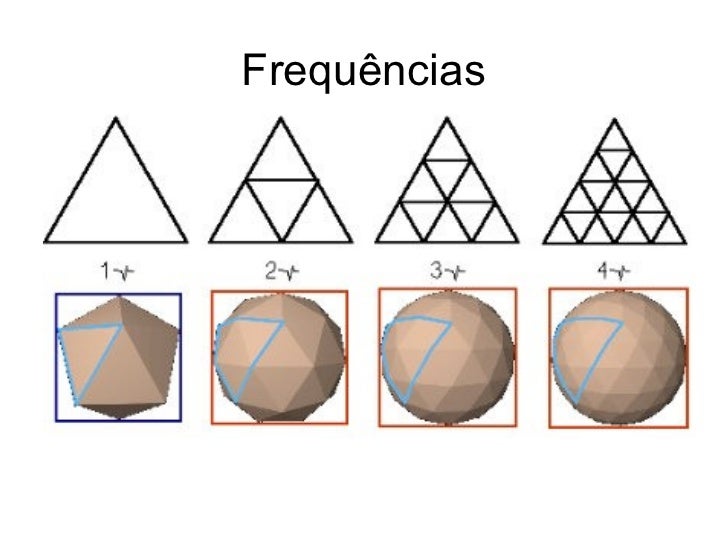
def circle(x,y,r,c): lcd.hline(x-r,y,r*2,c) for i in range(1,r): a = int(math.sqrt(r*r-i*i)) # Теорема Пифагора! lcd.hline(x-a,y+i,a*2,c) # Нижняя половина lcd.hline(x-a,y-i,a*2,c) # Верхняя половина lcd.display() utime.sleep(0.1)
Если же нарисовать лишь конечные точки линий на границе круга — получится кольцо.
def ring(x,y,r,c): lcd.pixel(x-r,y,c) lcd.pixel(x+r,y,c) lcd.pixel(x,y-r,c) lcd.pixel(x,y+r,c) lcd.display() utime.sleep(0.1) for i in range(1,r): a = int(math.sqrt(r*r-i*i)) # Теорема Пифагора lcd.pixel(x-a,y-i,c) lcd.pixel(x+a,y-i,c) lcd.pixel(x-a,y+i,c) lcd.pixel(x+a,y+i,c) lcd.pixel(x-i,y-a,c) lcd.pixel(x+i,y-a,c) lcd.pixel(x-i,y+a,c) lcd.pixel(x+i,y+a,c) lcd.display() utime.sleep(0.1)
Шаг 4. Треугольники
Разобьём треугольник на две части горизонтальной линией. Закрасим его, двигаясь от верхнего угла вниз и от нижнего угла вверх
Закрасим его, двигаясь от верхнего угла вниз и от нижнего угла вверх
Рисование границ треугольника — задача очень простая. Это — всего лишь три прямых линии.
def triangle(x1,y1,x2,y2,x3,y3,c): # Рисуем границы треугольника lcd.line(x1,y1,x2,y2,c) lcd.line(x2,y2,x3,y3,c) lcd.line(x3,y3,x1,y1,c)
А вот рисование закрашенного треугольника — это уже гораздо более сложная задача. Подробности об этом можно почитать здесь.
Предлагаемый метод похож на тот, который мы использовали для закрашивания кругов — для закрашивания треугольника рисуют прямые линии, касающиеся его границ.
Эту задачу легче решить в том случае, если речь идёт о треугольнике, имеющем вертикальную верхнюю или нижнюю сторону. Если такой стороны у треугольника нет, то исходный треугольник можно разделить на две части горизонтальной линией и закрасить получившиеся треугольники по отдельности. Всё это звучит довольно-таки просто, но для практической реализации этого механизма нужна серьёзная математика.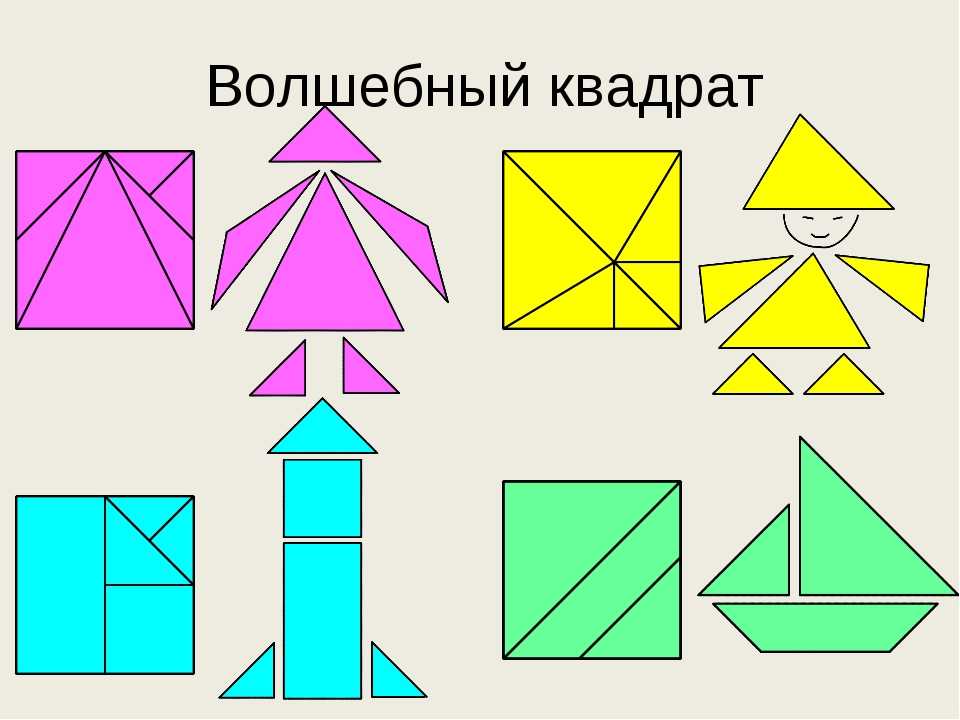 Правда, что хорошо, для того, чтобы пользоваться математикой, понимать её не обязательно. А именно, я создал команду, обращение к которой вызывает выполнение довольно-таки сложных действий.
Правда, что хорошо, для того, чтобы пользоваться математикой, понимать её не обязательно. А именно, я создал команду, обращение к которой вызывает выполнение довольно-таки сложных действий.
c = colour(0,255,0) tri_filled(x1,y1,x2,y2,x3,y3,c) lcd.display()
Полный код можно найти здесь, а результаты работы кода показаны в видеофрагменте, приведённом в следующем разделе. В коде программы содержится несколько команд utime.sleep(0.1), предназначенных для того, чтобы замедлить работу кода до такого уровня, чтобы можно было бы наблюдать за происходящим.
Шаг 5. Замедленная видеосъёмка процесса вывода треугольника, круга и кольца
Замедленная видеосъёмка
Шаг 6. Эксперименты с дисплеем
Эксперименты с дисплеем
Обычно я, когда покупаю и исследую новый дисплей, а потом пишу об этом, включаю в статью раздел, в котором экспериментирую с этим дисплеем (эти эксперименты я называю «Workout-примерами»). Делаю я это для того, чтобы помочь разработчикам понять, подойдёт ли он для их проектов. Вот — такой раздел для дисплея, описываемого в этом материале. Он выполняет всё то, что выполняют другие исследованные мной дисплеи. Это позволяет сравнивать скорость вывода информации и качество формируемой картинки. Здесь я использую джойстик и кнопки, вывожу тригонометрические графики и нечто вроде столбчатых диаграмм, показываю текст разных размеров, градиенты, а теперь — и круги с треугольниками.
Делаю я это для того, чтобы помочь разработчикам понять, подойдёт ли он для их проектов. Вот — такой раздел для дисплея, описываемого в этом материале. Он выполняет всё то, что выполняют другие исследованные мной дисплеи. Это позволяет сравнивать скорость вывода информации и качество формируемой картинки. Здесь я использую джойстик и кнопки, вывожу тригонометрические графики и нечто вроде столбчатых диаграмм, показываю текст разных размеров, градиенты, а теперь — и круги с треугольниками.
Надеюсь, вам понравилось то, что вы видели.
Программа, в которой всё это реализовано, получилась довольно длинной — 828 строк кода. Но её удалось уложить хотя бы в такой размер только благодаря тому, что этому миниатюрному экрану не нужен огромный фрейм-буфер. Это — реальный плюс экранов, состоящих из небольшого количества пикселей, если речь идёт о необходимости работы с большими объёмами графического кода.
Из кода этой программы, там, где выводятся круги и треугольники, убраны все задержки. Её скорость меня впечатлила, но в её распоряжении имеется очень небольшой буфер для копирования данных через SPI при каждой перерисовке экрана.
Её скорость меня впечатлила, но в её распоряжении имеется очень небольшой буфер для копирования данных через SPI при каждой перерисовке экрана.
Шаг 7. Вывод фотографий
Фотография, выведенная на дисплее
На предыдущем рисунке показана фотография, которую я сделал в Катманду, в храмовом центре Сваямбунатх.
В исходном виде это был .RAW-файл, сформированный фотоаппаратом Canon. Для вывода фотографии на дисплее мне понадобилось выполнить следующие действия:
- Я преобразовал файл в формат JPG, обрезал картинку, выдержав соотношение сторон, соответствующее разрешению в 160×80 пикселей, а после этого изменил размер изображения до 160×80 пикселей. Я это делал в Photoshop, но то же самое можно сделать и в бесплатном редакторе Gimp.
- Я преобразовал файл в новый RAW-формат, где, вместо 3-байтового цвета используется 2-байтовый цвет.
- Файл был скопирован на Pi Pico с Raspberry Pi 4 с использованием
rshell.
- Изображение было выведено на экран с использованием соответствующей программы и подходящего драйвера экрана.
Как видите, немалая часть этой работы заключается в предварительной подготовке изображения. Если вы хотите сделать что-то подобное — всё необходимое можно найти здесь.
Шаг 8. Компьютерная графика основана на математике
В этом проекте использовалось следующее:
- Базовая арифметика: счёт, вычисления, работа с процентными значениями, сравнение величин.
- Теория множеств: мэппинг и маскировка битов.
- Представление чисел в разных системах счисления при работе с битами и байтами: в двоичной, шестнадцатеричной и десятичной.
- Геометрия: круги, треугольники, прямоугольники, линии, точки.
- Координатная геометрия: рисование точек и отрезков.
- Теорема Пифагора.
- Тигонометрия: радианы, синус, косинус.

- Списки и суффиксы/указатели: байтовые массивы.
- Теория вероятностей: случайные числа.
Применяете ли вы Raspberry Pi Pico в своих проектах?
геометрия — Как круг просто набор треугольников?
Задавать вопрос
спросил
Изменено 10 месяцев назад
Просмотрено 15 тысяч раз
$\begingroup$
Я как-то должен нарисовать, как круг состоит из треугольников, но я не понимаю, как это возможно.
Может ли кто-нибудь помочь мне и дать несколько идей?
- геометрия
$\endgroup$
14
$\begingroup$
Мы можем думать о круге как о «связке» прямоугольных треугольников с гипотенузой, исходящей из центра.
Альтернативно, мы можем аппроксимировать круг, это можно сделать, например. как на следующем рисунке:
$\endgroup$
$\begingroup$
Вторая картинка в ответе Ребекки показывает, что окружность может быть сколь угодно точно аппроксимирована правильным многоугольником с достаточно большим количеством сторон.
Площадь каждого из этих треугольников равна 1/2 произведения основания на высоту, а высота приблизительно равна радиусу круга, а сумма оснований равна длине окружности многоугольника. Следовательно, площадь многоугольника в 1/2 раза больше, чем радиусная высота, умноженная на длину окружности.
Может возникнуть соблазн подумать, что это показывает только то, что площадь круга составляет приблизительно 1/2 радиуса, умноженного на длину окружности.
Но просто предположим, что площадь круга отличается от 1/2 радиуса, умноженного на длину окружности, на невообразимо крошечную, но не нулевую величину. Затем можно сделать разность меньше этой крошечной суммы, выбрав такое же невообразимо большое количество сторон многоугольника. Вывод: площадь круга ровно 1/2 длины окружности умножить на радиус.
Затем можно сделать разность меньше этой крошечной суммы, выбрав такое же невообразимо большое количество сторон многоугольника. Вывод: площадь круга ровно 1/2 длины окружности умножить на радиус.
Такие люди, как Лейбниц и Эйлер, просто сказали бы, что существует бесконечно много бесконечно тонких треугольников, а площадь круга равна сумме их площадей.
$\endgroup$
0
$\begingroup$
В дополнение к ответу Ребекки, вы также можете аппроксимировать круг, начав с вписанного равнобуквенного треугольника и нарисовав больше треугольников по краям:
Вы можете продолжать добавлять треугольники по краям предыдущих, чтобы максимально приблизиться к кругу
$\endgroup$
1
$\begingroup$
В компьютерной графике принято разбивать фигуры на треугольники. Компьютеры любят треугольники. Недостатком является то, что треугольники имеют прямые края, поэтому их требуется много, чтобы создать ИЛЛЮЗИЮ кривой. Круг на самом деле не является кучей треугольников, но может быть почти кучей треугольников. Исчисление основано на аналогичной идее
Компьютеры любят треугольники. Недостатком является то, что треугольники имеют прямые края, поэтому их требуется много, чтобы создать ИЛЛЮЗИЮ кривой. Круг на самом деле не является кучей треугольников, но может быть почти кучей треугольников. Исчисление основано на аналогичной идее
$\endgroup$
1
$\begingroup$
Вот 50 треугольников, вращающихся вокруг вершины:
А вот 50 треугольников, вращающихся вокруг центра:
$\endgroup$
Трудности и запросы | |||
Меня зовут Мэрилин Это школьный вопрос. С уважением, | |||
Привет Мэрилин, Сначала я расскажу вам свои предположения о том, как выглядит ваша картина.
Неизвестная область — это то, что осталось за пределами круга, между окружность и внешнюю сторону каждого треугольника. Эта неизвестная область разделен на шесть конгруэнтных частей (равных во всех отношениях — как треугольники «равны» во всех отношениях, включая площадь, длину стороны и длину дуга). Неясно, имеете ли вы в виду, что площадь одной дуги равна Пи (на самом деле не разделенный пирог, хотя произносится одинаково), или все шесть разделов, вместе взятые это Пи.  В дальнейшем я буду предполагать, что одна из внешних секций имеет
площадь числа Пи, так что площадь всех шести секций, вместе взятых, равна 6
раз Пи. Нам нужно найти радиус окружности, назовем его r. В дальнейшем я буду предполагать, что одна из внешних секций имеет
площадь числа Пи, так что площадь всех шести секций, вместе взятых, равна 6
раз Пи. Нам нужно найти радиус окружности, назовем его r.Я также буду использовать P для обозначения Пи (или примерно 3,14). Теперь есть много информации, которую мы можем получить из треугольников:
Из геометрии треугольников нам нужно сделать некоторые
алгебра. Поскольку мы знаем площадь, и нам нужен радиус, нам нужна формула
(или уравнение) для радиуса через площадь (в дальнейшем держим цель
по формуле). Площадь круга равна P*r 2 (r 2 означает r в квадрате, а * означает умножение) Площадь оставшихся участков
вне треугольников, но внутри круга (область, которую мы уже не
быть 6*P), также можно найти, вычитая площади треугольников из
площадь круга. Нам нужно найти площадь одного из равносторонних
треугольники. Метод 1 для вычисления площади треугольника Площадь треугольника равна b*h/2 Здесь необходима некоторая тригонометрия: Проведите линию от вершины к противоположной стороне, которая делит противоположную сторона пополам и находится под прямым углом. Это делит равносторонний треугольник на два равных прямоугольных треугольника, а новая сторона — это высота, назовите это х. Нам нужно найти ч. Используя trig в одном из прямоугольных треугольников, мы имеем sin60 = h/r Но sin60 = sqr(3)/2, где sqr(3) означает квадратный корень из трех, поэтому sqr(3)/2 = h/r умножить обе части на r, чтобы получить h = r*sqr(3)/2 r Теперь площадь одного равностороннего треугольника равно b*h/2 = (r)*(r*sqr(3)/2)/2 = (r 2 )*sqr(3)/4 Метод 2 расчета площади треугольника Формула Герона для площади треугольника: sqr(s*(s-a)*(s-b)*(s-c)),
где a,b,c — стороны, а s — половина периметра. Напомним, что площадь круга минус площадь все шесть треугольников — это площадь оставшихся участков. Из этого мы можем теперь составим уравнение: P*r 2 — 6*(r 2 )*sqr(3)/4 = 6*P Для определения r требуется некоторая алгебраическая помощь: Фактор r 2 на левая сторона (r 2 )*(P-6*sqr(3)/4) = 6*P Получить r 2 быть самим собой путем деления: r 2 = 6*P/(P-6*sqr(3)/4) Возьмите квадратный корень из обе стороны: r = sqr(6*P/(P-6*sqr(3)/4)) Использование порядок операций для расчета на калькуляторе (при P=3,14): r= 5,896. | |||

