Примеры блок – Назовите примеры применения блока. Назовите примеры применения блока

Блок — урок. Физика, 7 класс.

Блок является простым механизмом, который используют для подъёма тяжёлых грузов.

Блок состоит из закреплённого на оси диска, по окружности которого имеется жёлоб для скольжения в нём, к примеру, верёвки.

 

Блоки подразделяют на два вида:

1. неподвижный блок;

2. подвижный блок.

  

У неподвижного блока ось диска закреплена, в связи с чем во время подъёма груза диск только крутится вокруг своей оси. Выигрыш в силе (экономия силы) при таком виде блока отсутствует, но такой блок позволяет изменить направление действия силы, что часто необходимо для удобства.

  

Неподвижный блок (на рисунке мы видим направление действующих сил)

 

У подвижного блока диск перемещается вместе с грузом, в связи с чем достигается двукратная экономия силы.

 

 

Подвижный блок (на рисунке мы видим только направление действующих сил)

 

При решении задач можно выполнять рисунок схематически, не показывая подвешенное тело, указывая только действующие силы. При этом вес тела можно обозначить буквой P, а силу тяги — F.

 

Если груз весит \(100\) Н, то для его подъёма при помощи неподвижного блока потребуется сила в \(100\) Н, в свою же очередь, при помощи подвижного блока потребуется сила всего в \(50\) Н.

 

Обрати внимание!

Несмотря на то, что подвижный блок даёт экономию силы, которая необходима для подъёма груза, в целом для подъёма груза необходимо совершить такую же работу, как и в случае неподвижного блока!

Если объединить неподвижный и подвижный блоки, можно достичь не только изменения направления прилагаемой силы, но и экономии силы.

 

Примеры применения блоков:

 

Механизм блока используется в лодочных лебёдках.

 

При подъёме грузов подъёмными кранами используют блоки.

 

Работу различных подъёмников обеспечивает механизм блока.

Блок (механика) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Блок.

Блок — простое механическое устройство, позволяющее регулировать силу. Представляет собой колесо с жёлобом по окружности, вращающееся вокруг своей оси: жёлоб предназначен для каната, цепи, ремня и т. п.

Неподвижный блок — ось блока в обоймах, закреплённых на балке или стене: меняет направление силы.

Условие равновесия блока:

F=fmg{\displaystyle F=fmg}

где

F{\displaystyle F} — прилагаемое внешнее усилие,

m{\displaystyle m} — масса груза,

g{\displaystyle g} — ускорение свободного падения,

f{\displaystyle f} — коэффициент сопротивления в блоке: для цепей ~1.05, для верёвок ~1.1.

При отсутствии трения для подъёма нужна сила, равная весу груза.

Подвижный блок — ось блока в обоймах, к которым прикрепляется груз, и блок вместе с ними может двигаться: меняет

величину силы. Если концы верёвки, обхватывающей блок, составляют с горизонтом равные между собой углы, то действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом; отсюда, если верёвки параллельны (то есть когда дуга, обхватываемая верёвкой, равна полуокружности), то для подъёма груза потребуется сила вдвое меньше, чем вес груза, то есть:

F=12fmg{\displaystyle F={1 \over {2}}fmg}

При этом груз пройдёт расстояние, вдвое меньшее пройденного точкой приложения силы F, соответственно, выигрыш в силе подвижного блока равен 2.

Фактически, любой блок представляет собой рычаг: в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило:

во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии.

Иными словами, работа, совершаемая при перемещении груза на какое-либо расстояние без использования блока, равна работе, затрачиваемой при таком же перемещении груза с применением блока при условии отсутствия трения (в реальном блоке всегда присутствуют некоторые потери).

Полиспаст — система из нескольких подвижных и неподвижных блоков (обычно попарно). Простейшая такая система изображена на рисунке и даёт выигрыш силы в ~2 раза при любом направлении приложения усилия.

В отличие от шкива, блок вращается на оси свободно и не передаёт усилия с оси на ремень или с ремня на ось.

Подвижный и неподвижный блок, с примерами задач

Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.

Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).

Неподвижный блок

Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.

Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:

   

Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:

   

так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.

Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:

   

при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:

   

Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.

Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.

Комбинация неподвижных блоков

Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.

Условие равновесия для рычага на рис.2 станет формула:

   

Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.

Подвижный блок

Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:

Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:

   

Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:

   

Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.

Золотое правило механики

Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.

В виде формулы «золотое правило№ можно записать так:

   

где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .

Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:

   

Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:

   

Если силы и уравновешены, то блок покоится или движется равномерно.

Примеры решения задач

Рычаг и блок в физике. Примеры систем рычагов и блоков

С древних времен человечество стремилось любыми способами облегчить свой физический труд. Средством для решения этой проблемы стали простые механизмы. В данной статье рассматриваются такие изобретения, как рычаг и блок, а также система рычагов и блоков.

Что такое рычаг и когда его начали применять?

Вероятно, каждый с детства знаком с этим незамысловатым механизмом. В физике рычагом называется совокупность балки (стержня, доски) и одной опоры. Служит рычаг для поднятия тяжестей либо для сообщения телам скоростей. В зависимости от положения опоры под балкой рычаг может приводить к выигрышу либо в силе, либо в перемещении грузов. Следует сказать, что рычаг не приводит к сокращению работы как физической величины, он лишь позволяет перераспределить ее выполнение удобным образом.

Систему рычагов с давних пор использует человек. Так, существуют свидетельства, что ее использовали древние египтяне при строительстве пирамид. Первое математическое описание эффекта рычага относится к III веку до нашей эры и принадлежит оно Архимеду. Современное объяснение принципа работы этого механизма с привлечением понятия момента силы возникло лишь в XVII веке, во времена становления классической механики Ньютона.

Правило рычага

По какому принципу работает рычаг? Ответ на этот вопрос содержится в понятии о моменте силы. Последним называют такую величину, которая получается в результате умножения плеча силы на ее модуль, то есть:

M = F*d

Плечо силы d представляет собой расстояние от точки опоры до точки приложения силы F.

Когда рычаг выполняет свою работу, то на него действуют три различные силы:

• внешняя сила, приложенная, например, человеком;
• вес груза, который человек стремится переместить с помощью рычага;
• реакция опоры, действующая со стороны опоры на балку рычага.

Реакция опоры уравновешивает две другие силы, поэтому рычаг не совершает поступательного движения в пространстве. Чтобы он не совершал еще и вращательное движение, необходимо, чтобы сумма всех моментов сил оказалась равной нулю. Момент силы всегда отсчитывается относительно некоторой оси. В данном случае этой осью является точка опоры. При таком выборе оси плечо воздействия силы реакции опоры будет равно нулю, то есть эта сила создает нулевой момент. На рисунке ниже показан типичный рычаг первого рода. Стрелками отмечены внешняя сила F и вес груза R.

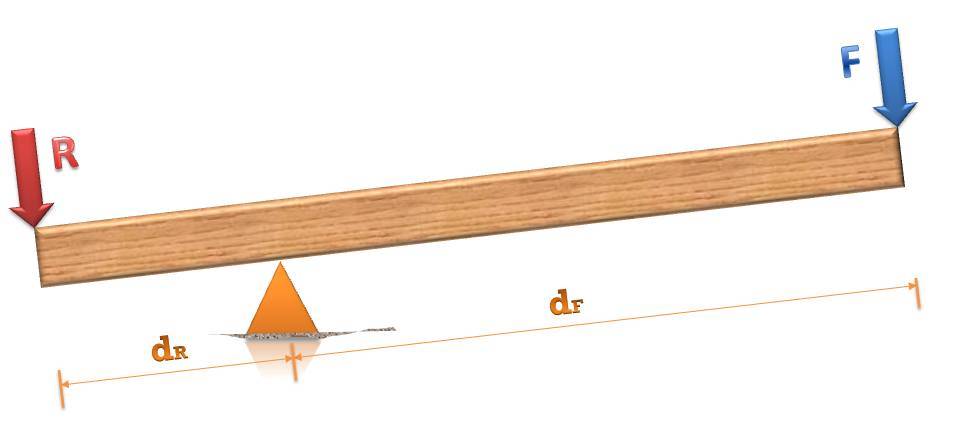
Записываем сумму моментов для этих сил, имеем:

R*d_R + (-F*d_F) = 0

Равенство нулю суммы моментов обеспечивает отсутствие вращения плеч рычага. Момент силы F взят с отрицательным знаком потому, что эта сила стремится повернуть рычаг по часовой стрелке, сила же R стремится совершить этот поворот против часовой стрелки.

Переписывая это выражение в следующих формах, получим условия равновесия рычага:

R*d_R = F*d_F;

d_R/d_F = F/R

Мы получили записанные равенства, используя концепцию момента силы. В III же веке до н. э. греческие философы не знали об этой физической концепции, тем не менее Архимед установил обратную зависимость отношения действующих на плечи рычага сил от длины этих плеч в результате экспериментальных наблюдений.

Записанные равенства говорят о том, что уменьшение длины плеча d_R способствует появлению возможности с помощью небольшой силы F и длинного плеча d_F поднимать большие веса R грузов.

Что такое блок в физике?

Блок — это еще один простой механизм, который представляет собой круглый цилиндр, имеющий борозду по периметру цилиндрической поверхности. Борозда служит для закрепления веревки или цепи. Блок имеет ось вращения. На рисунке показан пример блока, демонстрирующий принцип его работы.

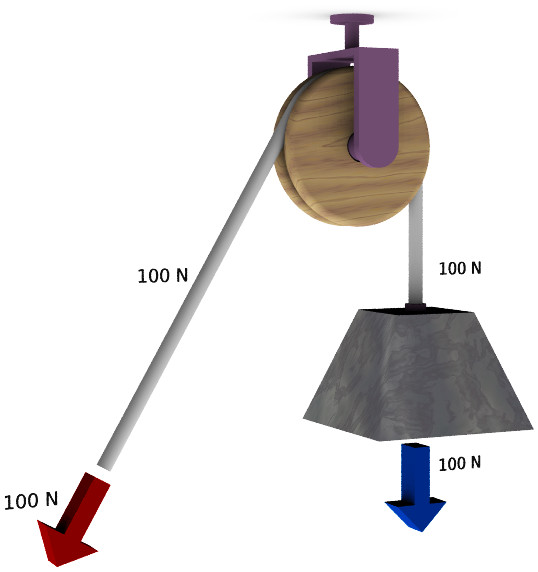
Этот блок называется неподвижным. Он не дает выигрыша в силе, однако позволяет изменить ее направление.

Помимо неподвижного, существует подвижный блок. Система из подвижного и неподвижного блоков показана ниже.

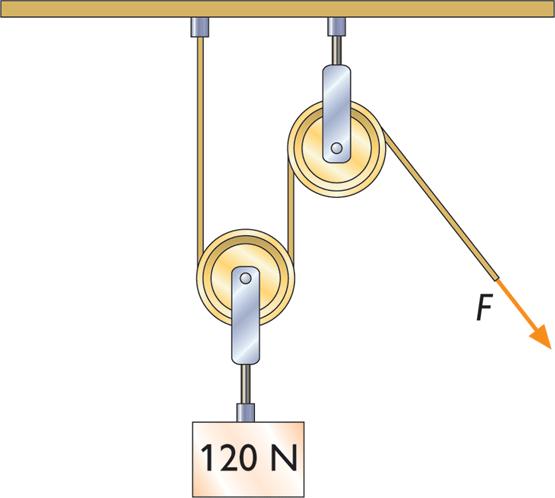
Если правило моментов применить к этой системе, то мы получим выигрыш в силе в два раза, но при этом во столько же раз проиграем в пути (на рисунке F = 60 Н).

Система рычагов и блоков

Как уже упоминалось в предыдущих пунктах, рычаг может применяться для выигрыша в пути или силе, блок же позволяет выиграть в силе и изменить направление ее действия. Эти свойства рассматриваемых простых механизмов применяются в системах рычагов и блоков. В этих системах каждый элемент принимает некоторое усилие и передает его другим элементам так, что на выходе мы получаем первоначальное усилие.

Простота работы рычага и блока и гибкость их конструкционного использования позволяют из такой совокупности составлять сложные механизмы.

Примеры использования систем простых механизмов

По сути, любые машины, которые нас окружают, представляют собой системы рычагов и блоков. Приведем самые известные примеры:

• печатная машинка;
• пианино;
• грузоподъемный кран;
• раскладные строительные леса;
• регулируемые кровати и столы;
• совокупность костей, суставов и мышц человека.

Если известно входное усилие в каждой из этих систем, то выходная сила может быть рассчитана с помощью последовательного применения правила рычага к каждому элементу системы.

20 примеров сайтов, построенных на блоках

Блоки в веб-дизайне — не новая технология с точки зрения верстки, но лишь недавно повсеместное использование плотно прилегающих блоков без просветов стало настоящим трендом. Это отличный способ для проектов, в которых большое количество информации нужно уложить максимально емко. Сегодня мы собрали примеры использования таких блоков в веб-дизайне.

 

 

---

marieseverac.com 

---

compliments.dk 

---

telstra2015ar.interactiveinvestorreports.com

---

vdesign.com.ar 

---

margauxbernard.com

---

mancini-traverso.com

---

pollenize.org

---

pucajewels.com

---

mirageparties.co.uk

---

z.ultranoir.com

---

playthinkcreative.it

---

indoffice.ru

---

m-goldstein.com 

---

oxenmade.com

---

tweetsfortreats.com

---

unheap.com

---

warben.com 

---

leapxd.com

---

enginedigital.com

---

thewebkitchen.co.uk

---

bodhicycling.be

---

benefunder.org

Автор подборки — Дежурка

Смотрите также:

• Сайты с нестандартными макетами
• Вдохновляющий минимализм в веб-дизайне
• Эксперименты с формами в веб-дизайне

Подвижный блок, теория и примеры задач

Определение и общие понятия о подвижном блоке

На рис. 1(b) подвижный блок представлен как рычаг с плечами разной величины. При этом точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Из рис. 1(b) следует, что плечо силы в два раза больше, чем плечо силы , значит величина силы F в два раза меньше, чем модуль силы P:

   

Мы получили, что подвижный блок дает выигрыш в силе в 2 раза. Подвижный блок позволяет силой величиной F уравновесить силу величиной 2F. Условие равновесия подвижного блока можно записать как:

   

где F – усилие, которое прикладывают. Выражение (1) записано без учета силы трения в блоке. Если силу трения пытаются учесть, то формулу (1) могут записать в виде:

   

где k – коэффициент сопротивления для блока, так, например, для веревки .

Часто применяют сочетание подвижного блока и неподвижного. При этом неподвижный блок служит только для удобства. Он не дает выигрыша в силе, однако он позволяет изменять направление действия силы.

И так, подвижный блок обладает свободной осью и назначен для того, чтобы изменять величину прилагаемого усилия. В том случае, если концы веревки, которые обхватывают блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза требуется в два раза меньше, чем вес поднимаемого груза.

Золотое правило механики

Простые механизмы не приводят к выигрышу в работе. Во сколько раз получается выигрыш в силе, во столько же раз имеется проигрыш в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.

Золотое правило было сформулировано в древности как: «То, что выиграно в силе, проиграно в пути (расстоянии)». Все простейшие механизмы хорошо иллюстрируют это правило. Следовательно, если при использовании подвижного блока мы получаем выигрыш в силе, равный двум, то расстояние, которое пройдет груз при поднятии будет в два раза меньше, чем пройдет точка, к которой приложена сила.

Подвижный блок можно использовать для выигрыша в расстоянии, при этом проигрывая в силе. Для этого силу прикладывают к его оси. При этом, если ось блока пройдет расстояние равное s, то конец веревки пройдет путь равный .

Примеры решения задач

Неподвижный блок, все формулы и примеры задач

Общие сведения о неподвижном блоке

Неподвижный блок относят к простым механизмам (рис.1). Будем считать, что блок вращается без трения. Если веревка натянута и не скользит по блоку, то на блок действуют две силы натяжения веревки ( и ). Точки приложения этих сил на рис. 1 обозначены как A и B, которые расположены на окружности блока.

Условия равновесия блока определяют из условия равновесия моментов сил, которые к нему приложены. Блок на рис.1 будет находиться в равновесии, если силы , так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.

Вместо блока можно использовать гладкую неподвижную опору. При этом через нее перекидывают веревку или канат, скользящие по опоре, однако при этом существенно увеличивается сила трения.

Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, значит, равны работы.

Комбинация блоков

Для получения выигрыша в силе используют комбинации блоков, например, двойной блок. При этом используют блоки разного радиуса, которые соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку крепится веревка таким образом, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в данном случае неодинаковы. Двойной блок работает как неравноплечный рычаг. На рис.2 представлена схема двойного блока.

Условием равновесия такого рычага является выражение:

   

Двойной блок можно считать преобразователем силы. Прикладывая меньшую силу к веревке, приложенной к блоку большего радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.

Золотое правило механики

Формулировка «Золотого правила»: Отношение перемещений точек, к которым приложены силы в блоке всегда обратно отношению сил, которые приложены к этим точкам.

Для двойного блока, если для равновесия блока сила должна быть в n раз больше по величине, чем сила , то при вращении блока путь, который пройдет точка приложения силы будет в n раз меньше, чем путь который проходит точка приложения силы .

Золотое правило было сформулировано в древности как: «То, что выиграно в силе, проиграно в пути». В математическом виде это правило представим как:

   

Золотое правило стало первой самой простой формулировкой закона сохранения энергии. Золотое правило механики выполняется для случаев, когда движения простых механизмов равномерно или почти равномерно. Так, при вращении двойного блока концы веревок переместятся на расстояния, которые связаны с радиусами блоков как:

   

Следовательно, для того чтобы выполнялось золотое правило для двойного блока должно выполняться условие:

   

Когда силы и будут уравновешены, то блок должен покоиться или двигаться равномерно.

Примеры решения задач на неподвижный блок